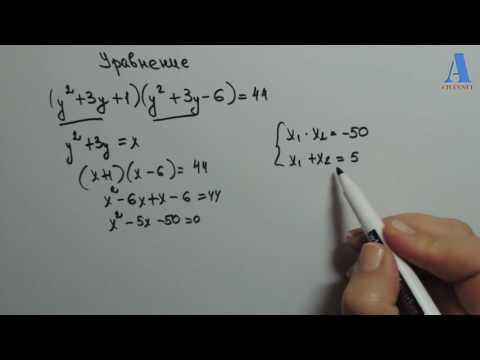Решение уравнений через переменную т

Видео:Решение уравнения методом замены переменнойСкачать

Метод замены переменной

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение (x+frac) буквой (t).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение (sin x) буквой (t).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Примеры использования метода замены переменной

Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя (x^2) на (t).

Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: (±1); (±) (frac) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!

Пример. Решить неравенство: (log^2_3⁡x-log_3⁡x-2>0)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Уравнение с заменой через t. Решение уравнений с помощью замены

Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Метод замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x (t) , или t = t (x) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f (x) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x (t) . Тогда мы должны выразить функцию f (x) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f (x) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x (t) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t (x) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ (x) — это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x — это функция от t .
(2) ,
где t — это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2) . Положим t = x 2 + x . Тогда
;
;

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x)′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b — постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции .
.
ln 2 — это постоянная. Вычисляем интеграл.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

.
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.

Решение уравнений методом замены переменных

Большинство жизненных задач

решаются как алгебраические уравнения:

приведением их к самому простому виду.

Цель урока : организовать учебную деятельность учащихся по освоению ими способов решения целых уравнений высших степеней методом замены переменной; познакомить учащихся с понятиями, приёмами решения возвратных и симметрических уравнений.

Задачи: образовательная: продолжать развивать умение применять метод замены

переменной при решении уравнений; формирование умения видеть один и тот же метод решения уравнений в различных ситуациях; сформировать представление о методах и способах решения нестандартных задач и алгебраических уравнений на уровне, превышающем уровень государственных образовательных стандартов;

развивающая: развитие мышления учащихся; развитие памяти; развитие

логического мышления, способности четко формулировать свои мысли; развитие воображения учащихся; развитие устной речи.

воспитательная: воспитание наблюдательности; воспитание аккуратности

при выполнении записей на доске и в тетради; воспитание самостоятельности при выполнении практических работ.

Актуализация и систематизация знаний.

Задание №1 . Разгадайте кроссворд. Ответы записывайте только в именительном падеже.

4.Чем является выражение для квадратного уравнения? (дискриминант)

6.Значение переменной, при которой уравнение обращается в верное равенство. (корень)

8.Уравнение вида
, где
. (биквадратное)

9.Французский математик, имеющий отношение к квадратным уравнениям. (Виет)

10.Уравнение, в котором левая и правая части являются целыми выражениями. (целое)

11. Уравнения с одной переменной, имеющие одинаковое множество корней. (равносильные)

1.Множество корней уравнения. (решение)

2.Решение уравнения
. (ноль)

3.Равенство, содержащее переменную. (уравнение)

5.Квадратное уравнение, в котором один из коэффициентов b или с равен 0. (неполное)

7. Квадратное уравнение, в котором первый коэффициент равен единице. (приведенное)

Чему мы сегодня посвятим наше занятие? (Решению уравнений)

Задание №2 . Каким способом вы решали бы уравнения каждой из групп?

ОТВЕТЫ: Примеры группы 1) лучше решать разложением на множители с помощью вынесения общего множителя за скобки или с помощью формул сокращенного умножения.

Примеры группы 2) лучше решать способом группировки и разложения на множители.

Примеры группы 3) лучше решать введением новой переменной и переходом к квадратному уравнению.

1 Какой множитель вы вынесли бы за скобки в примерах группы 1 ?

Как вы сгруппировали бы слагаемые в примерах группы 2 ?

Что бы вы обозначили через новую переменную в примерах группы 3?

Как можно разложить на множители многочлен
?

Сегодня на уроке вы покажете свои знания по теме «Решение уравнений методом замены переменной»

Запишите в тетрадях тему урока.

Сегодня на занятии мы рассмотрим один из способов решения уравнений высших степеней — метод замены переменной; познакомимся с понятиями, приёмами решения возвратных и симметрических уравнений.

Искусство производить замену переменных заключается в том, чтобы увидеть, какая замена будет более рациональна и быстрее приведет к успеху.

Решите уравнение. (задание у доски одновременно решают 2 ученика.)

а) (Первый ученик решает у доски с объяснением.)

б) (Второй учащийся решает уравнение молча, затем объясняет решение, класс слушает и задает вопросы, если что-то непонятно.)

1 ученик Замена:
.

2 ученик Замена:
.

(Дополнительно для тех, кто раньше справился с предыдущими уравнениями).

(Ход решения учащимися комментируется с места.)

РЕШЕНИЕ: Вынесем общий множитель: ,

откуда
или
, т.е.

Ответ:

Углубление и расширение знаний

Продолжаем работу. Вы видите на слайде уравнение: х 4 -5х 3 +6х 2 -5х+1=0.

Каким способом вы предложите его решить? Как нам быть?

Возможно ли решить его в рамках школьных программ по математике? Можно ответить нет. Ведь стандартные методы решения уравнений в школе предусматривают решение уравнений не выше второй степени. Но можно вспомнить, что отдельные уравнения более высоких степеней в школе все-таки решались. Правда, способы их решения суть творческое применение известных способов, сведения их к решению одного или нескольких уравнений степени не выше второй.

Посмотрите очень внимательно на это уравнение? Что вы заметили?( в этом уравнении коэффициенты равноудалённые от концов равны)

Ребята, уравнение такого вида, когда коэффициенты, равноудалённые от концов совпадают, называются возвратными . Это уравнение сводится к квадратному с помощью подстановки .

Предлагаю вам следующий алгоритм их решения:

Алгоритм решения возвратных уравнений.

1.Разделить обе части уравнения на х 2 .

2.Сгруппировать слагаемые (первый с последним, второй с четвёртым).

Привести уравнение к виду а + с = 0

3. Ввести новую переменную t = ,тогда выполнено t 2 = , т.е. = t 2 – 2.

4. Выполнить подстановку и решить квадратное уравнение.

5.Вернуться к замене и решить получившиеся уравнения.

Ребята изучают алгоритм.

Ученик у доски по алгоритму и с помощью учителя решает уравнение, остальные пишут в тетрадях.

6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.

6(х 2 + 1/х 2) – 5(х + 1/х) – 38 = 0.

Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2) = t 2 – 2, имеем:

6t 2 – 5t – 50 = 0.

t = -5/2 или t = 10/3.

Вернемся к переменной х. После обратной замены решим два полученных уравнения:

х 2 – 10/3 х + 1 = 0;

В проблему уравнений 3-й и 4-й степеней большой вклад внесли итальянские математики 16 века Н.Тарталья, А.Фиоре, Д.Кардано и др. В 1535 г. между А.Фиоре и Н.Тартальей состоялся научный поединок, на котором последний одержал победу. Он за 2 часа решил 30 задач, предложенных Фиоре, а сам Фиоре не смог решить ни одной, заданной ему Тартальей.

Ребята, и ещё одно уравнение я хочу вам сегодня предложить, я его взяла из сборника задач для подготовки к ОГЭ.

. ((х + 1)(x + 4))((х + 2)(x + 3)) = 24,

(х 2 + 5х + 4)(х 2 + 5х + 6) = 24.

Сделав замену х 2 + 5х + 4 = t, имеем уравнение

t(t + 2) = 24, оно является квадратным:

После выполнения обратной замены, легко находим корни исходного уравнения.

Творческий перенос знаний и навыков в новые условия.

В начале урока говорили о том, что если в уравнении есть повторяющиеся элементы, то можно применять метод замены переменной. Мы еще не умеем решать тригонометрические и иррациональные уравнения. Давайте посмотрим, сможем ли мы применять к ним этот метод, если будем знать, как решать простейшие тригонометрические и иррациональные уравнения.

Задание 1: Назвать замену переменной в следующих уравнениях.

Задание 2: Составить несколько уравнений, в основе решения которых лежит метод замены переменной.

Итак, ребята, наш урок подошёл к концу. Давайте подведём итоги нашего урока.

Какие цели мы ставили в начале урока?

Наши цели достигнуты?

Что нового мы узнали на уроке?

4х 4 – 8х 3 + 3х 2 – 8х + 4 = 0

. (уравнение итальянских математиков)

А закончить урок мне хочется словами великого учёного Эйнштейна А. :

« Мне приходиться делить своё время между политикой и уравнениями. Однако уравнение, по – моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно».

Спасибо за урок! До свидания!

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это всё так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

В элементарной математике выделяют два вида уравнений:алгебраические и трансцендентные.К алгебраическим уравнениям относятся:

линейное; квадратное; кубическое; биквадратное; уравнение четвертой степени общего вида; двучленное алгебраическое уравнение n-й степени; степенное алгебраическое; – возвратное (алгебраическое); – алгебраическое уравнение ой степени общего вида;

10. дробные алгебраические уравнения, т.е. уравнения, содержащие многочлены и алгебраические дроби (дроби вида

, где и – многочлены);

11. иррациональные уравнения, т.е. уравнения, содержащие радикалы, под которыми располагаются многочлены и алгебраические дроби;

12. уравнения, содержащие модуль, под модулем которых содержатся многочлены и алгебраические дроби.

Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. В нашей работе рассмотрим подробнее алгебраические уравнения.

В учебной и методической литературе традиционно рассматриваются специальные приёмы решения уравнений. Между тем специфика решения уравнений каждого раздела – дело второстепенное. По существу, применяются четыре основных метода:

Замена уравнения h (f(x))=h (g(x)) уравнением f(x)=g(x);

Метод замены переменной;

Метод разложения на множители;

Функционально-графический метод и их различные модификации.

Самый распространённый из них – метод замены переменной.

Исходя из этого, мы формулируем цель своей работы: изучить возможности метода замены неизвестного при решении алгебраических уравнений и продемонстрировать их применение в стандартных и нестандартных ситуациях. Для того, чтобы достичь поставленной цели необходимо решить следующие задачи:

1. Раскрыть содержание основных понятий и утверждений, относящихся к теории решения уравнений: решение уравнения, равносильность и следствие, общие методы решения уравнений.

2. Выявить возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ситуациях.

3. Осуществить типизацию приёмов введения новых неизвестных при решении алгебраических уравнений и выявить критерии их применимости

4. Составить комплект типовых задач, сводящихся к применению метода замены при решении уравнений, и продемонстрировать их решение.

1. Основные понятия и утверждения, относящиеся к теории решения уравнений

В первой главе нашей работы раскроем содержание основных понятий и утверждений, относящихся к теории решения уравнений.

С понятием «уравнение» на уроках математики мы знакомимся уже в начальной школе, а задача «решить уравнение», вероятно, наиболее часто встречающаяся задача. Тем не менее дать точное определение понятия «уравнение», точно определить, что значит «решить уравнение», не выходя далеко за рамки курса элементарной математики, мы не можем. Для этого необходимо привлекать весьма серьёзные логические и даже философские категории. Нам вполне достаточно знакомства с этими понятиями на уровне «здравого смысла».

Рассмотрим два уравнения А и В с одним и тем же неизвестным. Мы будем говорить, что уравнение В является следствием уравнения А, если любой корень уравнения А является корнем уравнения В.

Уравнения называются равносильными, если любой корень одного из них является корнем другого и наоборот. Таким образом, уравнения равносильны, если каждое из них является следствием другого.

Из данных определений следует, например, что два уравнения, не имеющие решений, равносильны. Если А не имеет решений, то В является следствием А, каково бы ни было уравнение В.

Определим понятие «решить уравнение». Решить уравнение – значит найти все такие значения входящих в него неизвестных, которые обращают уравнение в тождество. Эти значения называются корнями уравнения.

Процесс решения уравнений заключается в основном в замене данного уравнения другим, ему равносильным.

Как было ранее сказано, выделяют четыре наиболее общих метода, используемых при решении уравнений любых видов. Остановимся подробнее на каждом методе.

Метод замены уравнения h (f(x))=h (g(x)) уравнением f(x)=g(x) можно применять только в том случае, когда

— монотонная функция, которая каждое своё значение принимает по одному разу. Если данная функция немонотонная, то указанный метод применять нельзя, поскольку возможна потеря корней.

Суть метода разложения на множители заключается в следующем: уравнение

можно заменить:

Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние.Идея графического метода решения уравнения

такова: нужно построить графики функций , и найти точки их пересечения. Корнями уравнения служат абсциссы этих точек. Этот метод позволяет определить число корней уравнения, угадать значение корня, найти приближённые, а иногда и точные значения корней. В некоторых случаях построение графиков функций можно заменить ссылкой на какие-либо свойства функций (потому-то мы говорим не о графическом, а о функционально-графическом методе решения уравнений). Если, например, одна из функций возрастает, а другая – убывает, то уравнение либо не имеет корней, либо имеет один корень.Упомянем ещё одну довольно красивую разновидность функционально-графического метода: если на промежутке наибольшее значение одной из функций , равно и наименьшее значение другой функции тоже равно , то уравнение равносильно на промежутке системе уравнений.

Раскроем суть метода замены переменной: если уравнение

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Урок и презентация на тему: «Метод замены переменной. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Алгебраические задачи с параметрами, 9–11 классы

Этот метод довольно часто встречается при решении уравнений, и мы с вами им не раз пользовались.Его можно использовать в следующих случаях:

• Если исходное уравнение $f(x)=0$ имеет сложный вид, но его удалось преобразовать к уравнению вида $h(g(x))=0$.
• Нужно произвести замену переменных $u=g(x)$.
• Решить уравнение $h(u)=0$, найти корни $u_1$, $u_2$, … $u_n$.
• Ввести обратную замену $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$.
• Решить каждое из уравнений $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$. Корни каждого из уравнений и будут решениями исходного уравнения.

Метод замены переменной, требует хорошего навыка и опыта работы с уравнениями. После решения большого количества уравнений общий вид этих уравнений хорошо запоминается и придумать замену, приводящую к уже известным уравнениям, становится гораздо проще. Стоит также проверять все корни, полученные при замене уравнений и только после этого возвращаться к исходной переменной.

Пример.
Решить уравнение: $8x^6+7x^3-1=0$.

Решение.
Введем замену $y=x^3$. Тогда наше уравнение сводится к квадратному уравнению:
$8y^2+7y-1=0$,
$(8y-1)(y+1)=0$,
$y_1=frac$ и $y_2=-1$.

На данном этапе при решении более сложных уравнений следует проверить полученные корни.
Введем обратную замену: $x^3=frac$ и $x^3=-1$.
Корни данных уравнений найти легко: $x_1=frac$ и $x_2=-1$.

Введем замену: $u=sqrt<frac>$, тогда наше уравнение сводится к $u+frac=4$. $u^2-4u+4=0$, откуда $u=2$.

$2x+3=4(2x-1)$, решив линейное уравнение $х=1frac$.

Пример.
Решить уравнение: $2^x+2^=3$.

Решение.
Наше уравнение сводится к равносильному уравнению: $2^x+frac=3$.

Введем обратную замену: $2^x=2$ и $2^x=1$. Откуда: $х=1$ и $х=0$.

Пример.
Решить уравнение: $lg^2(x^2)+lg(10x)-6=0$.

Решение.
Преобразуем наше уравнение.
$lg^2(x^2)=(lg(x^2))^2=(2lg(x))^2=4lg^2x$.
$lg(10x)=lg10+lgx=1+lgx$.

Исходное уравнение равносильно уравнению: $4lg^2x+lgx-5=0$.

Введем обратную замену: $lgx=-1,25$ и $lgx=1$.
Ответ: $x=10^<-frac>$ и $x=10$.

Пример.
Решить уравнение: $sin(x)cos(x)-6sin(x)+6cos(x)+6=0$.

Решение.
Введем замену: $cos(x)-sin(x)=y$.

Исходное уравнение равносильно:
$frac+6y+6=0$,
$1-y^2+12y+12=0$,
$y^2-12y-13=0$,
$(y-13)(y+1)=0$.

Введем обратную замену: $cos(x)-sin(x)=13$ — очевидно, что решений нет, так как косинус и синус ограничены по модулю единицей.

Ответ: $x=frac+2πn$ и $π+2πn$.

Задачи для самостоятельного решения

Математика – это скважина, через которую логический ум может подглядывать за идеальным миром.

В школе ведущее место в курсе алгебры занимают рациональные уравнения. Именно на их изучение времени отводится больше, чем на любые другие темы. Связано это в первую очередь с тем, что уравнения имеют не только важное теоретическое значение, но и служат многим практическим целям. Огромное количество задач реального мира сводятся именно к решению различных уравнений, и только после того, как вы овладеете способами их решения, вы найдете ответы на различные вопросы науки и техники.

Для формирования умения решать рациональные уравнения самостоятельная работа ученика имеет огромное значение. Однако перед тем как переходить именно к самостоятельной работе, необходимо четко знать и уметь применять на практике все возможные методы решения рациональных уравнений.

Рассмотрим подробно на примерах метод замены переменных для решения рациональных уравнений.

Решить уравнение (2x 2 – 3x + 1) 2 = 22x 2 – 33x + 1.

Перепишем уравнение в виде

(2x 2 – 3x + 1) 2 = 11(2x 2 – 3x) + 1. Сделаем замену. Пусть 2x 2 – 3x = t, тогда уравнение примет вид:

Теперь раскроем скобки и приведем подобные, получим:

t 2 + 2t + 1 = 11t + 1;

В получившемся неполном квадратном уравнении вынесем общий множитель за скобки, будем иметь:

Теперь необходимо сделать обратную замену и решить каждое из полученных уравнений:

2x 2 – 3x = 0 или 2x 2 – 3x = 9

x(2x – 3) = 0 2x 2 – 3x – 9 = 0

x = 0 или x = 3/2 x = 3 или x = -3/2

Решить уравнение (x 2 – 6x) 2 – 2(x – 3) 2 = 81.

Применим формулу квадрата разности (a – b) 2 = a 2 – 2ab + b 2 . Запишем исходное уравнение в виде

(x 2 – 6x) 2 – 2(x 2 – 6x + 9) = 81. Теперь можно сделать замену.

Пусть x 2 – 6x = t, тогда уравнение будет иметь вид:

t 2 – 2t – 18 – 81 = 0;

По теореме Виета корнями полученного уравнения будут числа -9 и 11.

Сделаем обратную замену:

x 2 – 6x = -9 или x 2 – 6x = 11

x 2 – 6x + 9 = 0 x 2 – 6x – 11 = 0

(x – 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 = 3 – 2√5.

Ответ: 3 – 2√5; 3; 3 + 2√5.

Решить уравнение (x – 1)(x – 3)(x + 5)(x + 7) = 297 и найти произведение его корней.

Найдем «выгодный» способ группировки множителей и раскроем пары скобок:

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x 2 + 5x – x – 5)(x 2 + 7x – 3x – 21) = 297;

(x 2 + 4x – 5)(x 2 + 4x – 21) = 297.

Cделаем замену x 2 + 4x = t, тогда уравнение будет выглядеть следующим образом:

Раскроем скобки, приведем подобные слагаемые:

t 2 – 21t – 5t + 105 = 297;

t 2 – 26t – 192 = 0.

По теореме Виета определяем, что корнями полученного уравнения будут числа -6 и 32.

После обратной замены будем иметь:

x 2 + 4x = -6 или x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x – 32 = 0

Нет корней x 1 = -8; x 2 = 4

Найдем произведение корней: -8 · 4 = -32.

Найти сумму корней уравнения (x 2 – 2x + 2) 2 + 3x(x 2 – 2x + 2) = 10x 2 .

Пусть x 2 – 2x + 2 = t, тогда уравнение примет вид:

t 2 + 3xt – 10x 2 = 0.

Рассмотрим полученное уравнение как квадратное относительно t.

D = (3x) 2 – 4 · (-10x 2) = 9x 2 + 40x 2 = 49x 2 ; ≥≤

t 1 = (-3x – 7x) / 2 и t 2 = (-3x + 7x) / 2;

t 1 = -5x и t 2 = 2x.

Так как t = x 2 – 2x + 2, то

x 2 – 2x + 2 = -5x или x 2 – 2x + 2 = 2x. Решим каждое из полученных уравнений.

x 2 + 3x + 2 = 0 или x 2 – 4x + 2 = 0.

Оба уравнения имеют корни, т.к. D > 0.

С помощью теоремы Виета можно сделать вывод, что сумма корней первого уравнения равна -3, а второго уравнения 4. Получаем, что сумма корней исходного уравнения равна -3 + 4 = 1

Найти корень уравнения (x + 1) 4 + (x + 5) 4 = 32, принадлежащий промежутку [-5; 10].

Пусть x = t – 3, тогда x + 1 = t – 2; x + 5 = t + 2 и исходное уравнение принимает вид:

(t – 2) 4 + (t + 2) 4 = 32. Для возведения выражений в четвертую степень можно воспользоваться треугольником Паскаля (рис. 1);

(t – 2) 4 = t 4 – 4t 3 · 2 + 6t 2 · 2 2 – 4t · 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 · 2 + 6t 2 · 2 2 + 4t · 2 3 + 2 4 .

После приведения подобных слагаемых получим:

2t 4 – 2 · 6t 2 · 2 2 + 2 · 2 4 = 32;

t 4 + 6t 2 · 2 2 + 2 4 = 16;

t 4 + 24t 2 + 16 = 16;

t = 0 или t 2 = -24.

Второе уравнение не имеет корней, а значит t = 0 и после обратной замены

x = t – 3 = 0 – 3 = -3. Корень уравнения -3 принадлежит промежутку [-5; 10].

Как видим, при решении рациональных уравнений необходимо знать приведенные выше формулы и уметь правильно считать. Ошибки же чаще всего возникают при выборе замены и при обратной подстановке. Чтобы этого избежать, нужно расписывать подробно каждое действие, тогда ошибок в ваших решениях не будет.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Методы решения уравнений — обзор

В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Метод введения новой переменной (замены переменной)

Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) , где f , f₁ и f₂ – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x) . Введение переменной позволяет от исходного уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) перейти к уравнению с новой переменной f(t)=0 или f₁(t)=f₂(t) соответственно. Дальше находятся корни полученного уравнения с новой переменной: t₁, t₂, …, t_n . После этого осуществляется возврат к старой переменной, для чего составляется совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n . Решение этой совокупности дает интересующее нас решение исходного уравнения.

Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t 2 −3·t+2=0 с новой переменной t , которое имеет два корня t₁=1 и t₂=2 . Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2 , а решением второго является x=1,5 . Так методом введения новой переменной получено решение исходного уравнения: 1,5 , 2 .

Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Метод разложения на множители

Метод разложения на множители предназначен для решения уравнений f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁(x), f₂(x),…, f_n(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f₁(x)·f₂(x)·…·f_n(x)=0 решением совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.

Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x₁=1 . Логарифмическое уравнение тоже имеет единственное решение x₂=4 . Значит, совокупность уравнений имеет два решения x₁=1 , x₂=4 . Но области допустимых значений для исходного уравнения, которой является множество (3, +∞) , принадлежит лишь одно из решений x₁=1 , x₂=4 , а именно, x₂=4 . Оно и является единственным корнем уравнения .

Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод решения уравнений «дробь равна нулю»

Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0 . Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x 2 −4)=0 на ОДЗ для исходного уравнения.

Обоснование метода и примеры с решениями смотрите здесь.

Видео:Решение систем уравнений методом подстановкиСкачать

Метод решения уравнений через преобразования

Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.

Например, для решения уравнения 3·x 4 −48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3 . В результате получается равносильное уравнение x 4 =16 , причем очень простое в плане решения. Оно имеет два корня x₁=−2 и x₂=2 . Они и составляют решение исходного уравнения.

Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0 , имеющее два корня x₁=1 и x₂=−2 . Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.

Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.

Видео:Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

Метод решения уравнений, сводящихся к числовым равенствам

Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0 , а уравнение сводится к неверному числовому равенству 0=5 . Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0 . А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.

Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Функционально-графический метод

Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:

• Графический метод
• Метод, базирующийся на возрастании-убывании функций
• Метод оценки

Давайте рассмотрим их.

Графический метод

Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.

Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2 . Это единственный корень уравнения.

Метод, базирующийся на возрастании-убывании функций

Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3 (1−x) 3 +1=2 x несложно подобрать корень, им является число 1 . Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.

За более полной информацией следуйте сюда

Метод оценки

Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t₁ , t₂ , …, t_n , то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.

Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Метод освобождения от внешней функции

Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)) , где f , g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.

Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t) , где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x 2 +x−2=0 , которое имеет два корня x₁=−2 и x₂=1 . Из этих корней только x₁=−2 принадлежит ОДЗ для исходного уравнения. Следовательно, x₁=−2 – единственный корень исходного уравнения.

Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».

Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Метод решения уравнений через ОДЗ

Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.

Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7 . Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.

Более полная информация по этому методу решения уравнений содержится в этой статье.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Метод возведения обеих частей уравнения в одну и ту же степень

Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3) 2 . Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.

Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Метод решения уравнений по определению логарифма

По определению логарифма, как правило, решают уравнения следующего вида log_h(x)f(x)=g(x) , например, log₂(x 2 +4·x+3)=3 , log₂(9−2 x )=3−x , log_x(3·x lgx +4)=2·lgx и т.п.

Согласно методу решения уравнений по определению логарифма, решение уравнения log_h(x)f(x)=g(x) заменяется решением уравнения f(x)=(h(x)) g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения log_x(3·x lgx +4)=2·lgx можно перейти к уравнению 3·x lgx +4=x 2·lgx на ОДЗ для исходного уравнения.

Более полная информация содержится в основной статье.

Видео:9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Метод потенцирования

Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5) , и т.п. Метод заключается в замене решения уравнения log_h(x)f(x)=log_h(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0 , 3·x+5>0 .

Обоснование метода и примеры с подробными решениями смотрите в этой статье.

Видео:Целое уравнение и его корни. Алгебра, 9 классСкачать

Метод логарифмирования

Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 5 1−x =5 2·x+1 . Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1 , решение которого дает решение исходного уравнения.

Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких x lgx−1 =100 , .

Более детальная информация и примеры с решениями есть в этом материале.

🎦 Видео

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

решение уравнения с заменой переменнойСкачать