Видео:Решение биквадратных уравнений. 8 класс.Скачать
Конспект урока в 8 классе по теме: «Нахождение неизвестного числа»
план-конспект урока (8 класс) на тему
Урок математики в 8 классе по теме: «Нахождение неизвестного числа» проходит в режиме технологии уровневой дифференциации
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Скачать:
| Вложение | Размер |
|---|---|
| reshenie_uravneniy_urok_8_klass.doc | 94 КБ |
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Предварительный просмотр:
Урок математики в 8 классе
коррекционной школы VIII вида.
Тип урока: повторения, обобщения и систематизация знаний.
Главная дидактическая цель: повторить и систематизировать знания по теме: решение уравнений.
Технология обучения: технология уровневой дифференциации
Методы обучения: словесный, наглядный, практический, репродуктивный, объяснительно – иллюстративный.
II. Сообщение темы и целей урока.
IV. Актуализация чувственного опыта и опорных знаний с целью повторения пройденного.
VII. Повторение и систематизация имеющихся знаний под руководством учителя и в самостоятельной деятельности.
VIII. Подведение итогов. Оценки.
IX. Домашнее задание.
Тема: Нахождение неизвестного числа.
Базовый уровень — формировать умения решать уравнения (нахождение неизвестного слагаемого, уменьшаемого вычитаемого).
Повышенный уровень (в рамках коррекционной школы) – учить решать и составлять уравнения, используя правила нахождения неизвестного числа.
Базовый уровень – формировать умения решать уравнения и простые задачи на нахождение неизвестного числа, используя помощь учителя.
Повышенный уровень – формировать навык самостоятельной учебной деятельности на примере самостоятельного решения уравнений и задач, а также самостоятельного составления формулировок правил нахождения неизвестного числа.
Корригировать связную математическую речь учащихся, логическое мышление через установление причинно-следственных отношений, произвольную память и внимание.
Удовлетворять потребность в совместной деятельности ученика и учителя, а также в коллективной работе. Воспитывать взаимопомощь, доброжелательность, терпение, уважение, самоконтроль, взаимопроверку и самооценку.
Средства обучения: карточки: знать, уметь, решать, цветовая лента и книжки с цветом, карточки с правилами, таблицы с решением уравнений, дневники групп, таблички для групп (I, II, III), карточки с заданиями, ответами и числами.
Учебник «Математика 8 класс», изд. Москва «Просвещение», 2002г., авт. В.В. Эк.
II.Сообщение темы и целей урока.
(Мотивация учебной деятельности — уровневая).
Нахождение числа. 
-Назовите, какие действия, и числа мы сейчас повторяем?
-Какой буквой в выражениях обозначают неизвестное число?
-Как называются неизвестные числа в выражениях на сложение и вычитание?
-Какие цели вы ставите перед собой исходя из темы урока, используя слова: знать, уметь, решать?
-Каждый выберите для себя программу деятельности на уроке.
Знать 3 1задание
Уметь 4 1,2задания
Решать 5 1,2,3задания.
— Этот выбор необходим, чтобы в конце урока сопоставить результат с выполненной программой. В конце урока вы оцените свою деятельность, а я вашу.
1)Чтение примеров с названием компонентов.
(на доске две таблицы с примерами)
12 т 425 кг + 4 т 6,25 + 1,13
21 р.15 к. – 1р. 15 к. 0,172 – 0,1
62 785 + 3 4,008 – 0,008
1т – 998 кг 1 + 2 3
-В чём сходство примеров?
-В чём различие примеров первого столбика от примеров второго столбика?
-Исключите из первого столбика лишний пример.
-Исключите из второго столбика лишний пример.
Ученики сидят по группам, оформляют работу в тетрадях.
Под управлением учителя открывают карточку, за которой написано слово – «неизвестного» и читают тему урока.
=неизвестное слагаемое, уменьшаемое и вычитаемое.
Формулируют цели с помощью слов на доске.
Выбирают для себя программу, на полях под датой пишут заглавную букву слова (З, У, Р).
2)Различение целых и дробных чисел. Цветовая лента.
Учитель на карточках показывает числа.
Обыкновенные дроби
Целые числа, полученные при измерении
Целые числа, полученные при счёте
-Сегодня на уроке будем повторять действия сложение и вычитание с целыми числами и десятичными дробями.
3)Из двух выражений выбери то, которое соответствует условию задачи и является его решением.
Учитель читает задачу.
В школьной столовой для приготовления плова взяли 6 кг 300 г риса. В пакете осталось 1 кг 200 г риса. Сколько килограммов риса было до того, как начали готовить?
-Как в решении при вычитании называется неизвестное число?
-Как найти неизвестное уменьшаемое?
-Найдите неизвестное число и ответьте на вопрос, сколько килограммов риса было до того, как начали готовить?
IV.Актуализация чувственного опыта и опорных знаний с целью повторения пройденного.
Учитель показывает таблицы
(можно вывесить на доску).
I группа (нахождение неизвестного слагаемого)
Учащиеся различают их по названию и соотносят с нужным цветом с помощью индивидуальных цветовых книжек.
Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать
Конспект урока «Решение уравнений» (8 класс)
Конспект урока математики
Тема: Решение уравнений (2 урок).
Тип урока: комбинированный ( урок коррекции и обобщения знаний).
Цели урока:
- повторение и обобщение знаний в области решения уравнений;
- обеспечить понимание данного учебного материала всеми учащимися;
- воспитание терпеливости, упорства в достижении цели;
- культуры оформления решения уравнения и задач;
- развитие внимания, математически грамотной речи;
- развитие логического мышления, способности самостоятельно решать учебные задачи.
Оборудование: компьютер, интерактивная доска, ПО Smart Notebook, презентация для сопровождения урока, мультимедийный проектор, учебник Н.Я.Виленкина «Математика 6 класс», карточки для выполнения самостоятельной работы, листы самооценки.
Ход урока.
1. Организационный этап.
Мотивация (самоопределение) к учебной деятельности
Учитель приветствует учащихся, проверяет их готовность к уроку, знакомит
с целью, задачами и планом урока.
Ученикам раздаются листы самооценки (приложение 1), в которых они будут оценивать свою работу на разных этапах урока. За каждый правильный ответ на вопрос учителя, верно решенный пример, уравнение, задачу учащийся получает 1 балл – звездочку, которую заносит в свой оценочной лист.
2. Устная фронтальная работа с классом.
Актуализация знаний учащихся.
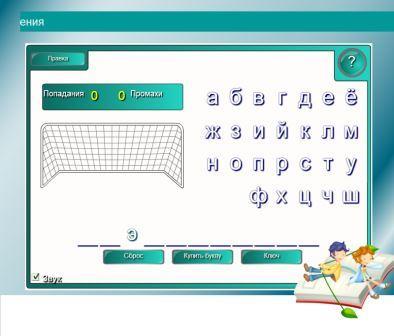
1) Повторяем определения (слайд 3)
Учитель предлагает ученикам отгадать зашифрованное слово, связанное с темой урока. В случае затруднения открывается «ключ» к заданию. Тот ученик, который знает ответ, выходит к доске и набирает угаданное слово.
1. Равенство, содержащее букву, значение которой надо найти (уравнение).
2. Число в выражении, которое записано с помощью числа, одной или нескольких букв (коэффициент).
3. Слагаемые, имеющие одинаковую буквенную часть (подобные).
4. Значение буквы, которое обращает уравнение в верное числовое равенство (корень).
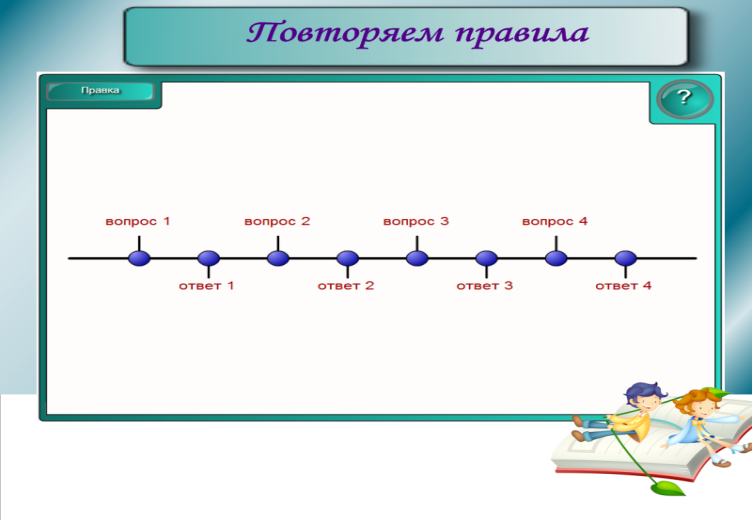
2) Повторяем правила (слайд 4, 5).
Учитель предлагает учащимся выбрать любой номер вопроса и ответить на него. Затем открывается верный ответ. При составлении алгоритма решения уравнений необходимо переместить таблички, расставив их в правильном порядке.
- Как раскрывают скобки, перед которыми стоит знак «+»?
- Как раскрывают скобки, перед которыми стоит знак «-»?
- Свойства уравнений.
- Как привести подобные слагаемые?
- Составить алгоритм решения уравнений.
Учащимся предлагается оценить себя на данном этапе урока (в оценочном листе они ставят себе * по количеству правильных ответов у доски или с места).
3) Вычислите устно.
Учащимся предлагается решить три примера, записать ответы в тетрадь.
Затем провести самопроверку (слайд 6).
Содержимое разработки
Конспект урока математики
Тема: Решение уравнений (2 урок).
Тип урока: комбинированный ( урок коррекции и обобщения знаний).
повторение и обобщение знаний в области решения уравнений;
обеспечить понимание данного учебного материала всеми учащимися;
воспитание терпеливости, упорства в достижении цели;
культуры оформления решения уравнения и задач;
развитие внимания, математически грамотной речи;
развитие логического мышления, способности самостоятельно решать учебные задачи.
Оборудование: компьютер, интерактивная доска, ПО Smart Notebook , презентация для сопровождения урока, мультимедийный проектор, учебник Н.Я.Виленкина «Математика 6 класс», карточки для выполнения самостоятельной работы, листы самооценки.
1. Организационный этап.
Мотивация (самоопределение) к учебной деятельности
Учитель приветствует учащихся, проверяет их готовность к уроку, знакомит
с целью, задачами и планом урока.
Ученикам раздаются листы самооценки (приложение 1), в которых они будут оценивать свою работу на разных этапах урока. За каждый правильный ответ на вопрос учителя, верно решенный пример, уравнение, задачу учащийся получает 1 балл – звездочку, которую заносит в свой оценочной лист.
2. Устная фронтальная работа с классом.
Актуализация знаний учащихся.
1) Повторяем определения (слайд 3)
Учитель предлагает ученикам отгадать зашифрованное слово, связанное с темой урока. В случае затруднения открывается «ключ» к заданию. Тот ученик, который знает ответ, выходит к доске и набирает угаданное слово.
1. Равенство, содержащее букву, значение которой надо найти (уравнение).
2. Число в выражении, которое записано с помощью числа, одной или нескольких букв (коэффициент).
3. Слагаемые, имеющие одинаковую буквенную часть (подобные).
4. Значение буквы, которое обращает уравнение в верное числовое равенство (корень).
2) Повторяем правила (слайд 4, 5).
Учитель предлагает учащимся выбрать любой номер вопроса и ответить на него. Затем открывается верный ответ. При составлении алгоритма решения уравнений необходимо переместить таблички, расставив их в правильном порядке.
Как раскрывают скобки, перед которыми стоит знак «+»?
Как раскрывают скобки, перед которыми стоит знак «-»?
Как привести подобные слагаемые?
Составить алгоритм решения уравнений.
Учащимся предлагается оценить себя на данном этапе урока (в оценочном листе они ставят себе * по количеству правильных ответов у доски или с места).
3) Вычислите устно.
Учащимся предлагается решить три примера, записать ответы в тетрадь.
Затем провести самопроверку (слайд 6).
8 – 70 = -19 + 100 = -18 – 46 =
Ответы: 54, -34, 27.
4) Проверьте свои знания (слайд 7)
Данное задание выполнено в виде теста. Необходимо решить устно пример. Ученик, который первым решит пример, выходит к доске и выбирает правильный ответ.
Найдите значение выражения:
56,3 – (90 + 56,3) = (90; -10,6; 120,6; -90)
-16 – (20,5 – 16 + 0,5) = (-21; 0; 16,5; 21)
— 10 х + 8х = (2х, -2х, 18х, -2)
-3у –(у — х) = (х + 4у, -у – 4х, х – 4у, у – 4х)
(х – 5) – (х + 5) = (10; -10; 5; 0)
Приведите подобные слагаемые:
4 а – b + 8a – 3b + ab = (12a – 3b + ab, 12a – 4b + ab , 4a – 4b + ab,
Чему равно значение k в уравнении -k = 7k ?
Укажите число, которое является корнем уравнения 12 – 7х = 20 + х.
Решите уравнение: 8 + х = х.
(уравнение не имеет корней, х = 8, х = -8, х = 0)
Ученикам предлагается оценить свою работу на этапе « устная работа».
3. Физкультминутка (слайд 8).
Ученики выполняют физкультминутку, просматривая видеофайл, повторяя упражнения под музыку вслед за героем видео.
4. Выполнение заданий.
Закрепление и коррекция знаний учащихся.
1) Решаем уравнения (слайд 9).
Ученики получают раздаточный материал ( приложение 3), самостоятельно решают уравнения. На работу отводится 5-8 мин. Затем проверяется решение, проводится самооценка. Проверка осуществляется с помощью интерактивной доски, можно посмотреть закладки с решениями уравнений на страничке в случае необходимости.
2х + 7 = 7х + 13 (-1,2)
4 (3 – 2х) + 24 = 2 ( 3 + 2х) (2,5)
0,2 (5у – 2) = 0,3 (2у – 1) – 0,9 (-2)
2) Решаем задачи (слайд 10)
Учащимся раздается раздаточный материал (приложение 2), им предлагается заполнить таблицы к задачам, составить уравнения. На работу отводится 10 мин.
Затем ученикам предлагается проверить свои работы, оценить свою деятельность на данном этапе урока. Проверка осуществляется с помощью ИД.
1. На одной полке в 5 раз больше книг, чем на второй. После того как с первой полки переложили на вторую 12 книг, на полках книг стало поровну. Сколько книг было первоначально на каждой полке?
2. На путь от поселка до города велосипедист затрачивает 2 часа, а пешеход — 6 часов. Скорость велосипедиста на 12 км/ч больше скорости пешехода. С какой скоростью идет пешеход? Используй при решении таблицу.
3. В детском наборе половина кубиков – зеленые, треть – красные, десятая часть – синие и еще 4 белых кубика. Сколько кубиков в детском наборе? (дополнительная задача)
В случае, если ученики справятся досрочно с заданиями, они получают дополнительные задания, за которые можно получить баллы.
5. Подведение итогов урока, коррекция знаний (слайд 11).
Для коррекции знаний учащихся решается несколько устных примеров на действия с рациональными числами, затем перейти к кадрам презентации, которые познакомит учащихся с выдающимся математиком Диофантом, с эпитафией-задачей, сделанной на его могиле. Учащимся предлагается попробовать разгадать зашифрованную надпись, определить, сколько лет прожил Диофант.
Ученики подводят итоги своей работы на уроке, подсчитывают количество заработанных баллов- звездочек, выставляют себе оценку (критерий выставления оценок зависит от количества заработанных * на уроке и может варьироваться учителем в том или ином классе).
6. Рефлексия. Задание на дом (слайд 12).
Учащиеся выбирают смайлика, который соответствует их настроению в конце урока.
Задание на дом: дифференцированные индивидуальные задания
Видео:Дробно-рациональные уравнения. 8 класс.Скачать
Конспект урока на тему: Решение уравнений 8 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Тема урока: РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ.
« О СКОЛЬКО НАМ ОТКРЫТИЙ ТРУДНЫХ
ГОТОВИТ ПРОСВЕЩЁННЫЙ ДУХ…».
* привести в систему знания учащихся по заданной
* выработать умения использовать алгоритм решения
* повышение культуры математических вычислений;
* творческое мышление, желание поиска решения;
* развивать умения применять теоретические знания
* привитие интереса работы в группах;
* воспитание навыков сознательного усвоения знаний;
* чувство взаимовыручки и поддержки;
* карточки — билеты с вопросами;
* бланки учёта ответов;
ОСНОВНЫЕ ЭТАПЫ УРОКА.
I . ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
Объявляется тема урока, цели и задачи, происходит
психологический настрой на продуктивную работу.
Работа с листами, устный опрос учащихся по билетам,
работа с раздаточным материалом.
Решение линейных уравнений на скорость в форме
IV . НАШИ СПОСОБНОСТИ.
Самостоятельное решение уравнений, по выбору уча-
щегося ( дифференцированный уровень заданий).
Исправление ошибок в неверном решении уравнения, сопоставление с решением уравнения учеником из команды
VI . ЭКСПЕРТНОЕ ЗАКЛЮЧЕНИЕ ЖЮРИ.
Подведение итогов, выставление оценок.
VII . ОБЪЯВЛЕНИЕ ИТОГОВ УРОКА.
Подведение итогов работы каждой команды.
Сравнение психологического настроя учащихся в начале урока и в конце.
I . ОРГАНИЗАЦИОННЫЙ МОМЕНТ ( СЛАЙД № 1).
Слова нашего сегодняшнего эпиграфа принадлежат перу гениального поэта, прозаика и драматурга. Давайте и мы с вами будем следовать словам А.С.Пушкина. Пусть каждый урок будет для вас открытием чего — то нового интересного,
Сегодня мне хотелось бы пригласить вас в замечательный
мир математики — в мир уравнений, в мир исследований.
В одной шуточной песенки поётся о том, что герой
этой песенки, начинающий волшебник, неумело обращался
с заклинаниями, в результате чего вместо грозы у него
получилась коза, а вместо утюга получился слон.
Так и нам, чтобы решить уравнение, тоже нужно совершить ряд превращений (алгебраических преобразова- ний) и делать это нужно осмотрительно. В ходе урока мы ещё раз убедимся, какая удивительная сила заключена в знании алгоритма решения уравнения, правила раскрытия скобок и правило переноса слагаемых из одной части уравнения в другую, правило приведения подобных слагае-
мых, как ловко эти правила работают при решении уравнений. И прежде всего, вы должны чётко знать, что главная задача при решении любого уравнения — свести его к уравнению простейшего вида, то есть к уравнению вида: ах = в и решив его найти корни уравнения ( слайд № ).
На доску проецируется задания для команд:
* решить уравнения и проверить является ли указанное
число корнем уравнения ( слайд № 2).
* Указать область допустимых значений уравнения. К
доске выходят представители команд для записи реше-
ния уравнений на доске ( слайд № ).
* Далее выходят по два ученика от каждой команды
команды для устного опроса по теоретическому мате-
риалу. Каждому учащемуся предлагается ответить на два
вопроса по выбору, из числа вопросов записанных на
билете, который вытягивает ученик.
* Остальные участники команды выполняют задания
теста по восстановлению пропусков в определениях и
понятиях. Задания в тестах одинаковые, только имеют
разный порядок и два варианта.
* После устных ответов проверяется работа учащих-
ся у доски, собираются тестовые задания для проверки
* В ходе разминки ученики распределяют между
собой решение предложенных десяти уравнений. По
очереди каждый член команды выходит к доске и
записывает решение уравнения на доске. В это время
эксперт оценивает решение уравнений у доски и
фиксирует его в листе опроса. Отмечается команда,
закончившая первой решение уравнений. При под-
ведении итогов ей присуждаются дополнительные
* 3(у – 1) – 2(у + 2) = 7. * 16х + 9 = 25.
* 3у – 4у = 14. * 3(х – 5) – 2(х-4) = 8.
* 9 + 13у = 35 + 26у. * -9х = 27.
* — 5у = — 35. * 81х — 71 = 50х + 22.
* 3у = — 9. * — 3х = — 18.
* Ученикам предлагаются примеры различного уровня сложности. Каждый учащийся может выбрать пример себе по силам и решить его и найти верное решение на слайде.
Для оценивания на оценку «3» надо решить три уравнения
из предложенных. Учашиеся, претендующие на « 5», реша-
ют примеры повышенной сложности у доски (слайд № ).
б) х — 7 = — 2. г) 3у — 7 = 11.
Работы сдаются эксперту, он определяет уровень на который претендовал ученик и оценивает его работу.
На экране проецируется решение уравнения, по одному представителю от каждой команды выходят решать
его у доски. Задача команды найти ошибки в решении
уравнения на интерактивной доске, установить их число,
объяснить, где допущены ошибки. Пока проходит обсужде-
ние в группах, ученик решает пример на доске. После
чего проходит объяснение решения и проверка ответа
а) 5(3 + 2а) — 11 = 6 – (8 – 4а) – первой команде.
б) 6(р – 4) + 2(3 -5р) = — 6 — второй команде.
VI . ЭКСПЕРТНОЕ ЗАКЛЮЧЕНИЕ ЖЮРИ.
В это время учащиеся выполняют самостоятельную работу на закрепление пройденного материала из учебника,
номера заданий проецируются на экране, задание выпо- лняются всей командой, учитывается быстрота и грамот-ность выполнения ( слайд № ).
VII . ПОДВЕДЕНИЕ ИТОГОВ УРОКА.
Учитель объявляет итоги экспертного заключения и
выставляет оценки за урок каждому ученику, составлена
таблица результативности, проверяется закрепляющая са-
мостоятельная работа. Подводятся итоги работы каждой
Рубрика « В МИРЕ ИНТЕРЕСНОГО» (слайд № 14 ).
Посмотрите на экран и ответьте, какую закономерность вы
находите у этих квадратов?
VIII . ДОМАШНЕЕ ЗАДАНИЕ ( слайд № 15 ).
📺 Видео
Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать
Неполные квадратные уравнения. Алгебра, 8 классСкачать
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать
Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Свойства арифметического квадратного корня. 8 класс.Скачать
Типы Химических Реакций — Химия // Урок Химии 8 КлассСкачать
Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать
Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать
Квадратное уравнение. 8 класс.Скачать
Биквадратные уравнения. 8 класс алгебра.Скачать
Теорема Виета. 8 класс.Скачать
Ирина Пономарева — Орбитальная механика: время и его измерение, системы координатСкачать
Свойства квадратного корня. Уравнение х2=а, 8 классСкачать
МАТЕМАТИКА 8 класс - Полные Квадратные Уравнения. Как решать Полные Квадратные Уравнения?Скачать
