Решение тригонометрических уравнений в паскале

Подпишись на новости, чтобы ничего не пропустить

Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью — не вся информация вошла в видеоролик.

На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже — в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.

Синтаксис функции Cos:

function Cos(Х : ValReal) : ValReal;

Синтаксис функции Sin:

function Sin(Х : ValReal) : ValReal;

О типе ValReal я рассказывал здесь.

Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.

ВНИМАНИЕ! Не в градусах, а в радианах!

Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.

Формула перевода градусов в радианы проста:

Радиан := Пи * Градус / 180

Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.

Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.

Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.

Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.

Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.

А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.

Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Что такое косинус и синус угла

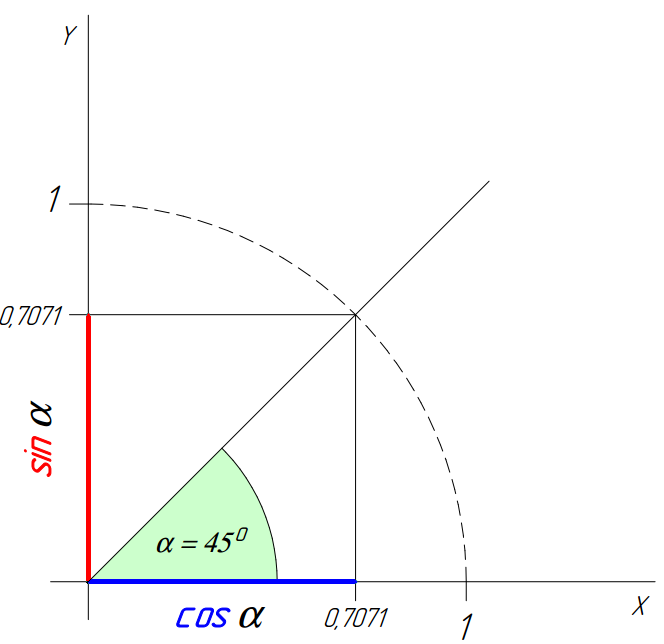
Для начала внимательно посмотрите на рисунок.

Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.

На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).

Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.

В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):

Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:

И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.

И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Решение тригонометрических уравнений в паскале

Команда solve, примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0,2 p ]. Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true.

В Maple символ _Z

обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид , где n – целые числа.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрические функции в паскале

Ниже приведены тригонометрические функции, используемые в языке программирования Pascal. Их аргумент может быть целым или вещественным; результат в любом случае – вещественный.

1 радиан = 180 / пи

sin(выражение) – синус угла, измеренного в радианах
sin(-pi / 6):4:1. Результат: -0.5
sin(0):4:1. Результат: 0.0
sin(pi / 2):4:1. Результат: 1.0

cos(выражение) – косинус угла, измеренного в радианах
cos(-pi / 6):4:1. Результат: 0.8
cos(0):4:1. Результат: 1.0
cos(pi):4:1. Результат: -1.0

arctan(выражение) – арктангенс
arctan(1e35):8:5. Результат: 1.57080
arctan(0):4:1. Результат: 0.0
arctan(-1):8:5. Результат: 0.78540

Pers.narod.ru. Алгоритмы. Некоторые математические расчёты на Паскале

Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.

Возведение в произвольную степень на Паскале

Требуется вычислить значение с = a b . В зависимости от значений основания a и показателя степени b , вычисление степени может быть реализовано по-разному.

Если a > 0 , а b может принимать произвольные вещественные значения, используем известную формулу a b = exp (b * ln a) :

Если b – целое число (вообще говоря, «не слишком большое» по модулю), а a – любое (не равное нулю при b ), возведение в степень может быть реализовано с помощью цикла:

Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:

Вычисление корня произвольной степени на Паскале

Стандартная функция sqrt умеет извлекать только квадратный корень.

Извлечь корень степени n (где n – натуральное) из числа a можно всегда, кроме случая, когда a и при этом n четно. Извлечь корень степени n из числа a означает возвести число a в степень 1/n . При этом знак корня совпадает со знаком a . Ниже приводится код функции, вычисляющей корень произвольной степени n от своего аргумента a :

Вычисление логарифмов на Паскале

Стандартная функция ln вычисляет только натуральный логарифм. Для вычисления логарифмов по другим основаниям можно применить формулу log _a b = ln b / ln a :

В частности, для вычисления десятичного логарифма lg b можно записать:

Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале

В Паскале имеется стандартная функция arctan для вычисления арктангенса.

Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.

Для вычисления y = arcsin x , где, конечно, |x| , можно применить один из следующих способов:

на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).

Для вычисления z = arccos x , где |x| , можно использовать тот факт, что сумма арксинуса и арккосинуса некоторого значения равна прямому углу:

Вычисление полярных углов на Паскале

Полярным углом точки с координатами (x,y) , отличной от начала координат, называют угол между положительным направлением оси Ox и направлением из начала координат на данную точку. При этом угол отсчитывается против часовой стрелки. Строго говоря, полярный угол не всегда равен arctg (y/x) , это верно лишь при x > 0 . Кроме того, при делении большого значения y на малое x возможно переполнение. Показанная ниже функция вычисляет полярный угол fi , лежащий в промежутке от -pi до +pi , для любой точки с координатами (x,y) , не совпадающей с началом координат:

Проблема с приведением типов на Паскале

Начинающие «паскалисты» нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие «баги». Вот простейший пример.

Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer , а потом «испорченный» результат переписали в переменную типа Longint . ничего не изменит и

Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint . А вот

рулит, получите свои 200000 🙂 Указанная ошибка часто встречается в программах начинающих. Чтобы её не повторять, помните – выражение в Паскале должно быть приведено к нужному типу в процессе его вычисления, а не после его окончания или при присваивании.

Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью – не вся информация вошла в видеоролик.

На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже – в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.

Синтаксис функции Cos:

function Cos(Х : ValReal) : ValReal;

Синтаксис функции Sin:

function Sin(Х : ValReal) : ValReal;

О типе ValReal я рассказывал здесь.

Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.

ВНИМАНИЕ! Не в градусах, а в радианах!

Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.

Формула перевода градусов в радианы проста:

Радиан := Пи * Градус / 180

Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.

Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.

Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.

Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.

Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.

А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.

Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.

Видео:Математика это не ИсламСкачать

Что такое косинус и синус угла

Для начала внимательно посмотрите на рисунок.

Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.

На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).

Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.

В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):

Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:

И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.

И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.

💡 Видео

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Решение тригонометрических уравнений. 10 класс.Скачать

Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Тригонометрия в ЕГЭ может быть простойСкачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать

Математика. Тригонометрические уравненияСкачать

Тригонометрические уравнения | Борис ТрушинСкачать

Решение тригонометрических уравнений методом вспомогательного углаСкачать

Решение тригонометрических уравнений. Метод понижения порядка. 10 класс.Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Решение тригонометрических уравнений. 10 класс.Скачать