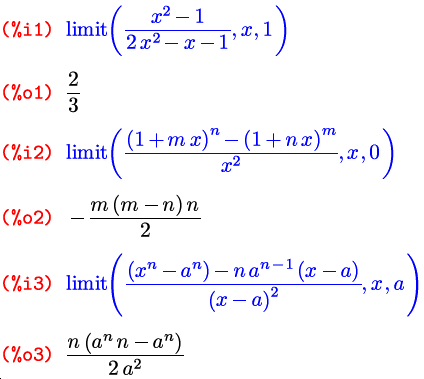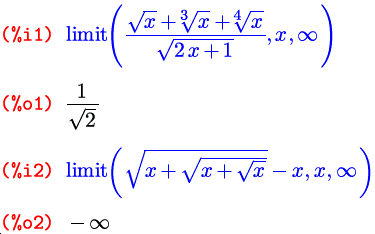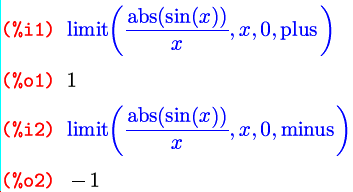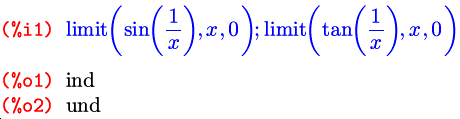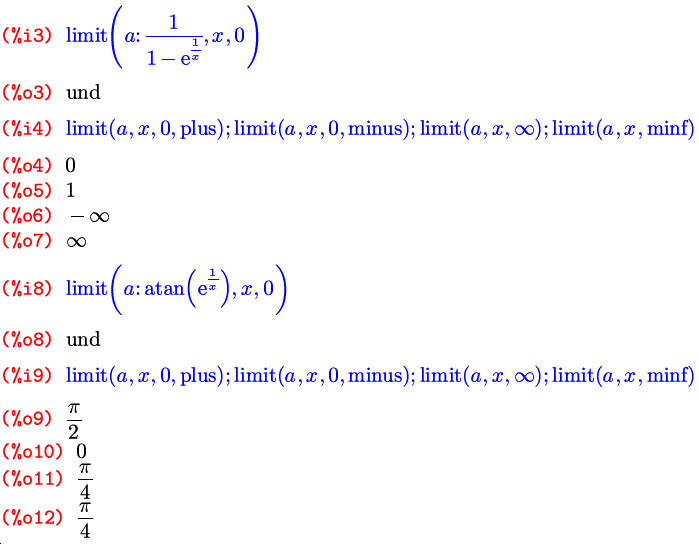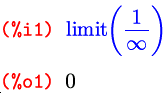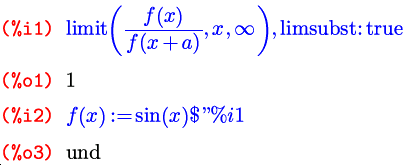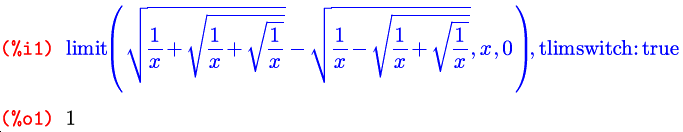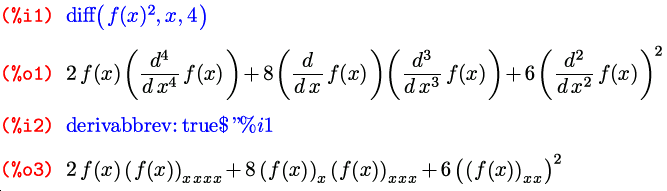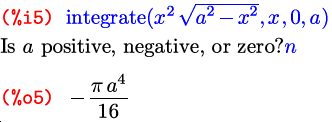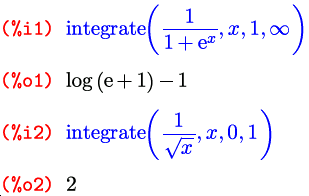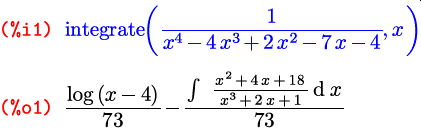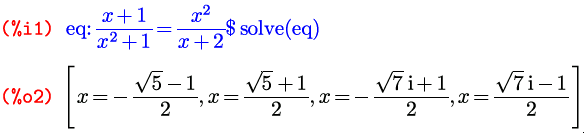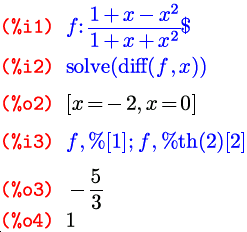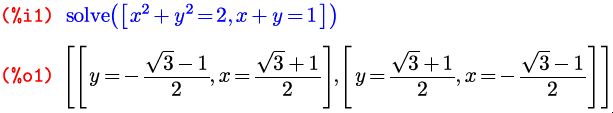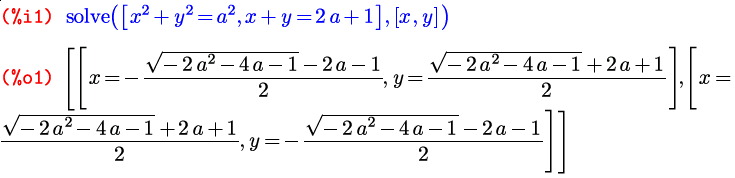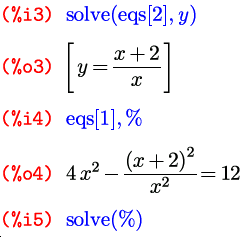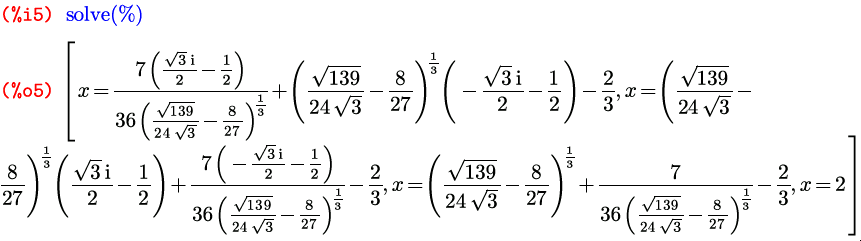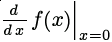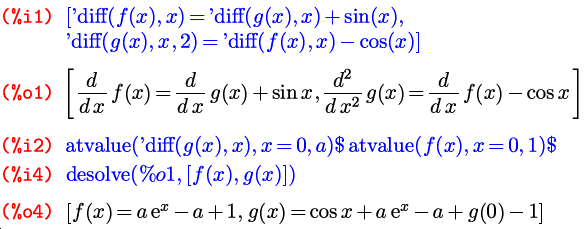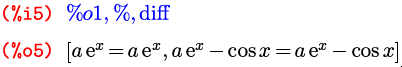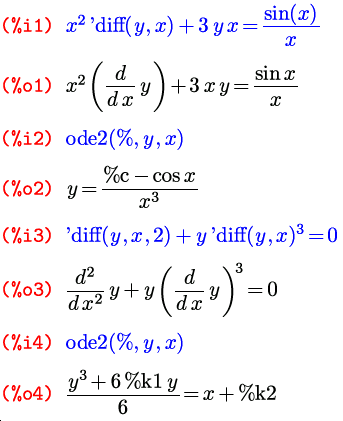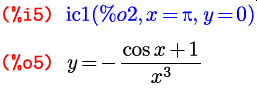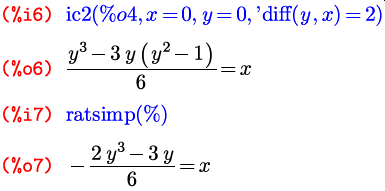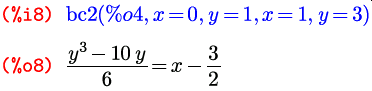Решение тригонометрических уравнений в maxima

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Решение физических и математических задач с Maxima

Доступная литература и сеть Интернет в качестве «электронного помощника» студентов и школьников обычно позиционирует пакет MathCad, изредка — Maple или Mathematica. Материал данной главы содержит ряд разнородных задач, которые решались разными авторами вручную или при помощи MathCad.

7.1 Операции с полиномами и рациональными функциями

Рассмотрим решение с помощью Maxima нескольких задач из классического сборника под редакцией М.И. Сканави. В Maxima «пошаговое» упрощение выражений с последовательным использованием стандартного набора примитивов (формул суммы или разности кубов, формул возведения суммы или разности в степень и т.п.) выполнить сложно, поэтому результат являются фактически справочным, на который следует ориентироваться при решении вручную, при помощи ручки и бумаги.

7.1.1 Упрощение алгебраических выражений

Упростить выражение и вычислить его, если даны числовые значения параметров:

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Maxima

Материал из CustisWiki

Maxima — система компьютерной алгебры, реализованная на языке Lisp.

Maxima имеет широчайший набор средств для проведения аналитических вычислений, численных вычислений и построения графиков. По набору возможностей система близка к таким коммерческим системам как Maple и Mathematica. В то же время она обладает высочайшей степенью переносимости. Это единственная из существующих систем аналитических вычислений, которая может работать на всех современных операционных системах, на компьютерах, начиная от самых мощных, заканчивая наладонниками.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Содержание

Видео:Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

История

Maxima произошла от системы «Macsyma», разрабатывавшейся в MIT (Massachusetts Institute of Technology) с 1968 по 1982.

Вариант продукта (известный как DOE Macsyma) сопровождался профессором Уильямом Шелтером в Техасском Университете с 1982 до своей смерти в 2001.

В 1998, Шелтер получил от Департамента энергии разрешение опубликовать исходный код DOE Macsyma под лицензией GPL, и в 2000 он создал проект «Maxima» на SourceForge для поддержания и развития «DOE Macsyma», переименованного в Maxima.

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Введение

Видео:Решение тригонометрических уравнений. 10 класс.Скачать

Обзор

Maxima может использоваться как мощный калькулятор:

Maxima поддерживает точные вычисления с большими числами, размер которых ограничен только ресурсами вашего компьютера.

Например, вычислим , а затем возьмем корень 25-степени из результата:

Знак «%» ссылается на специльную переменную, хранящую результат последней операции. Знак «^» — оператор возведения в степень.

Однако основное назначение компьютерной алгебры — не численные вычисления, а скорее, символьные операции. Поиграем с полиномом :

и первообразных (неопределенных интегралов):

Maxima может преобразовывать тригонометрические выражения в канонические конечные тригонометрические ряды (Fourier sums):

Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Первые шаги

Maxima ориентирована на минималистический интерфейс командной строки — т. е. сеанс работы состоит из последовательных команд пользователя и полученных на них ответов.

Команда — это некое выражение, возможно многострочное, оканчивающееся точкой с запятой «;». Например на команду:

будет получен ответ:

Если вы забудете ввести «;» — Maxima будет терпеливо (т. е. без каких-либо сообщений об ошибках) продолжать ввод ввод, пока вы ее не введете «;».

Можно вместо точки с запятой завершить команду знаком доллара «$», тогда вывод этой команды будет заглушён, то есть, команда будет обработана и результат будет вычислен, но не выведен на экран.

Введем какое-нибудь выражение с переменной:

Ответ Maxima содержит то же выражение, в неупрощенной форме:

Maxima выдает выражение-результаты, используя минималистические средства — текстовую отрисовку формул. Так в ответе «(%o2)» мы видим, что за счет исключения «*» из ответа, выражение выглядит «математическим», а не программистким.

Теперь раскроем скобки:

Т.е. человек вполне способен прочесть эту ASCII-формулу, однако, есть возможность получить эту формулу (c помощью функции «tex») в формате TeX:

Что, если отрисовать через TeX будет выглядеть так: .

Пользуясь этой возможностью, далее в этом введении, все математические формулы, получаемые от Maxima мы будем отрисовывать через TeX, что будет гораздо удобней для чтения, чем ASCII-графика, особенно в случае «многоэтажных» формул.

Итак, возведение в степень:

Обратите внимание на приоритет операций: x^3^4 есть

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Дифференцирование и интегрирование

Возьмем неопределенный интеграл для :

Продифференцируем результат для проверки:

И чтобы, не пугаться, упростим сумму рациональных выражений:

Повторим тоже самое для :

Если Maxima не смогла взять интеграл — она возвращает интеграл в «исходной форме»:

Разумеется, в TeX-форматировании интеграл будет выглядеть красивее:

В таком случае, можно помочь системе, выполнив замену переменных:

а затем проинтегрировав:

выполним обратную подстановку

Т.к. подынтегральное выражение — всюду определенная положительная функция, мы можем вычислить определенный интеграл , используя вычисленную первообразную «sfx»:

или переходя к значениям в плавающей арифметике:

Для проверки выполним численное интегрирование методом Ромберга:

Результаты аналитического и численного интегрирования совпадают с точностью 1e-10.

Осталось «сократить» экспоненты с логарифмами, перейдя к каноническому радикалу:

Видео:Решение тригонометрических уравненийСкачать

Решение полиномов

Нахождение нулей у полиномов от одной переменной — задача известная со школы. Поиграем с ней для демонстрации некоторых возможностей Maxima. Определим переменную poly:

Вычислим нули, используя функцию «solve»:

Мы получили ответ в виде двух равенств (с левыми и правыми частями) — если их преобразовать в множители, то мы должны получить исходный полином, в виде их произведения.

Воспользуемся механизмом лямбда-функций (по сути, безымянных функций). Лямбда функция

очевидным образом преобразует выражение-равенство, в множитель, равный нулю в точке равенства. Итак, применим функцию «map», применяющую нашу лямбда-функцию для всех элементов нашего списка уравнений:

Перемножим этот список:

И, раскрыв скобки, получаем исходный полином:

Видео:Работа с уравнениями и системами уравнений в программе MaximaСкачать

Тригонометрические преобразования

Чтобы преобразовать произведения синусов-косинусов, в триногометрический ряд Фурье, используется функция «trigreduce»:

Теперь избавимся от произведений в аргументах тригонометрических функций:

И наконец, упрощаем выражение, используя функцию «trigsimp», знающую тождество :

Упрощение тригонометрических выражений не всегда получается просто и быстро, как в приведенном примере, и в почтовых рассылках часто раздаются вопросы, «как мне упростить XXX?» или «почему Maxima не упрощает YYY?».

А пользуясь любым матсправочником с таблицей основных первообразных (например, справочником Бронштейна-Семендяева), легко получить более красивый результат: .

Попробуем упростить «влоб»:

Но применять дальше «trigexpand», для раскрытия sin(14*x) и cos(14*x) через sin(x) и cos(x) бесполезно — выражение сильно усложнится. Надо бы выразить sin(14*x) и cos(14*x) через sin(7*x) и cos(7*x), а для этого надо сделать подстановку, заменив 14*x на 2*y.

возвращаемся к исходным переменным:

Итак, мы показали на примере этой задачки, как важно использовать подстановки переменных при упрощении через «trigexpand». А вообще, это выражение можно было упростить одним действием:

Проверим результат интегрирования:

Выглядит просто, но чтобы сравнить с исходным выражением, надо выразить всю «тригонометрию» через 7x.

Итак, напомним еще раз назначение рассмотренных функций:

trigreduce преобразует тригонометрическое выражение как сумма слагаемых, каждое из которых содержит один синус или косинус. trigexpand «раскрывает» аргументы тригонометрических функций, согласно правилам тригонометрических функций от суммы углов. trigsimp упрощает тригонометрическое выражение, используя тождество . trigrat мощная функция — упрощение рационального тригонометрического выражения.

Видео:ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Разложение на простые дроби: шаг за шагом

Ответы Maxima всегда показывают готовый результат (если, конечно, системе удалось его получить), но не путь его вычисления.

Например, разложение на простые дроби выполняется функцией «partfrac»:

Обычно этого достаточно, ибо полученный результат вполне можно проверить. Однако, иногда требуется получить последовательность вычислений (например, если это часть домашней работы, и проверяющему недостаточно предьявить ответ).

Итак, попробуем вычислить разложение в «полуавтоматическом» (или «полуручном») режиме.

В данном случае, разложение на простые дроби — это сумма следующих элементарных дробей:

Приводим к общему знаменателю, и поименуем числитель этой дроби, как «n»:

Теперь осталось решить уравнение, «приравняв» числитель исходной дроби и числитель «n»:

Наконец, подставляем полученные коэффициенты:

Напомним, мы использовали следующие функции:

num возвращает числитель дроби. coeff возвращает коэффициент при переменной в заданной степени. solve решает систему линейных уравнений.

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Вычисление пределов

Maxima может вычислять пределы для широкого спектра как рациональных, так и трансцедентных функций.

Для рациональных функций, часто интересно посмотреть поведение функции на бесконечности:

Можно раскрыть и предел типа «0/0»:

Maxima умеет вычислять пределы «справа» и «слева», и честно сообщает, когда предел в заданной точке не определен:

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Вычисление рядов — конечных и бесконечных

Конечные суммы считаются сразу:

Но бесконечные ряды, по умолчанию не суммируются, выражение остается в исходном символьном виде:

Чтобы выполнить суммирование, нужно указать опцию «simpsum=true»:

Впрочем, над «непросуммированными суммами» можно выполнять операции, только операторы суммирования не будут сокращаться:

Для сокращения сумм, нужно использовать функцию «sumcontract»:

Версия 5.9.3. содержит баг 1517061

Далее, можно просуммировать, как мы уже делали выше:

Видео:Решение тригонометрических уравнений методом вспомогательного углаСкачать

Внешние ссылки

• Домашняя страница Maxima
• Maxima в Википедии.
• Вадим Житников-Компьютеры, математика и свобода
• Maxima – максимум свободы символьных вычислений
• Maxima: максимум удобства и функциональности
• WxMaxima — оконный интерфейс к Maxima.
• GNU TeXmacs — набор маттекстов в TeX, с плагинами доступа к различным CAS-системам, типа Axiom, Reduce, и в частности Maxima.

Любые правки этой статьи будут перезаписаны при следующем сеансе репликации. Если у вас есть серьезное замечание по тексту статьи, запишите его в раздел «discussion».

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Тихон Тарнавский. Maxima. Алгебра и начала анализа

Из встроенного функционала Maxima в первую очередь стоит обратить внимание на несколько групп функций: работу с пределами, дифференцирование, интегрирование, поиск решений уравнений — как «просто», так и дифференциальных.

Видео:Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать

«Предельничаем»…

Собственно полноценных функций для нахождения предела существует в Maxima аж одна. Но зато какая! Она может принимать три различных варианта списка аргументов, и кроме того, на ее действие влияют еще и три флага. Но давайте по порядку. Зовут эту функции вполне соответственно ее действию: limit ; и в самом стандартном варианте ее вызов выглядит как limit(выражение, переменная, точка) , то есть то, что в математической записи выглядит как lim _{x → a} f ( x ), в контексте Maxima запишется как limit(f(x), x, a) :

Maxima может искать пределы не только в конечных точках, но и на бесконечности. Среди стандартных обозначений программы существуют универсальные названия для разных бесконечностей: плюс-бесконечность записывается через inf (от слова infinity, как нетрудно догадаться), минус-бесконечность — через minf (от minus infinity); для комплексных чисел бесконечность, как известно, одна, и она (комплексная бесконечность) обозначается полным словом infinity . При работе с пределами все три обозначения могут как использоваться при вводе, так и возникать в виде найденного значения предела; отдельно здесь надо отметить один момент касательно работы с интерфейсом к Maxima в редакторе TeXmacs: символы inf и minf при выводе здесь отображаются в своей традиционной математической нотации, то есть как ∞ и −∞; символ вместо inf можно, кроме того, использовать еще и при вводе.

Второй вариант вызова функции limit() — это расширенная версия первого: limit(выражение, переменная, точка, направление) , для поиска односторонних пределов. Для предела справа в качестве «направления» указывается plus , для предела слева — minus :

Пределы справа и слева еще иногда называют соответственно пределами сверху и снизу. Хотя правильнее в таком случае говорить полностью: «предел при x , стремящемся к a сверху», в том числе чтобы не создавать путаницы с верхним и нижним пределами, которые суть совершенно другое.

Кроме упомянутых выше бесконечностей, на выходе возможно появление и еще двух обозначений, на случай, если заданный предел не существует: ind (от слова indefinite — неопределенный) и und (от слова undefined — опять же неопределенный). В документации первое из этих обозначений описано как indefinite but bounded (не определен, но ограничен), что дает предположить, что функция, не имеющая предела, при этом ограничена либо в окрестности предельной точки, либо на всей прямой. Какое из этих предположений имелось в виду, мне так и не удалось понять, потому как на практике ни одно из них не соответствует действительности. Вывода ind мне не удалось добиться ни на одной функции, радикально отличающейся от «канонической» (в том смысле, что фигурирующей в стандартном примере из комплекта) функции sin(1/x) .

Здесь все правильно, tan(1/x) не ограничена в окрестности нуля. А вот дальше начинаются чудеса:

Как видите, первая функция имеет конечные односторонние пределы в нуле, а вторая ограничена вообще на всей оси — и тем не менее… Но это, думаю, не столь критично: главное, что наличие любого из этих символов в качестве вывода дает нам понять, что искомого предела не существует.

Функция limit() в третьем варианте — limit(выражение) — предназначена уже не для поиска собственно пределов, а для упрощения выражений, содержащих символы inf и minf :

Выражения такого рода могут возникать, к примеру, при подстановках в формулы результатов вычисления каких-то других пределов или интегралов.

Такая способность — принимать различные списки аргументов — не является в Maxima чем-то особенным; она свойственна очень многим встроенным функциям, как и различное действие в зависимости от значений разнообразных переключателей. Это достаточно удобно: не нужно запоминать много разных имен функций (для поиска пределов, к примеру, используется исключительно функция limit ); для вычисления производных, в том числе и частных, — функция diff (с которой мы уже бегло ознакомились в первой статье и сейчас продолжим это знакомство); для нахождения интегралов, как определенных, так и неопределенных — функция integrate (с которой мы тоже сегодня познакомимся). Имена наиболее часто используемых функций запомнить несложно, а о дополнительных ключах или флагах, в случае чего, можно прочитать во встроенной справке, набрав ? имя-функции .

Об этих самых ключах к функции limit и осталось рассказать. Первый ключ называется lhospitallim и задает максимальное количество применений правила Лопиталя; название ключа и происходит от фамилии ученого, давшей название самому правилу, которая в оригинале пишется как L’Hospital. Напомню, правило это гласит, что в случае неопределенности вида 0/0 или можно продифференцировать числитель и знаменатель — и предел от этого не изменится. Ограничитель количества применений этого правила нужен для того, чтобы избежать зацикливаний, которые могут случиться для бесконечно дифференцируемых функций, у которых в данной точке равны нулю либо бесконечности все производные. По умолчанию значение lhospitallim равно четырем, и мне не удалось сходу придумать пример, когда этого не хватает — ведь функция поиска предела использует не только правило Лопиталя, но и другие соотношения; и для всех заданных мною соотношений двух функций с корнями выше четвертого порядка в искомой точке предел был успешно найден и при умолчательном значении.

Второй ключ к функции limit — это флаг limsubst , который, будучи выставлен в true , позволяет этой функции производить подстановки внутрь неизвестных выражений. По умолчанию этот флаг равен false , что исключает ошибки вроде такой:

И, наконец, последний дополнительный параметр — еще один флаг, по имени tlimswitch . По умолчанию он тоже выключен, а если его включить, функция limit будет, при невозможности найти предел другими способами, пытаться его найти путем разложения подпредельной функции в ряд Тейлора в окрестности заданной точки:

Но в случае поиска односторонних пределов, в тех точках, где они не равны между собой, то есть полного предела не существует, этим флагом нужно пользоваться с осторожностью: при его включении функция limit может вернуть в качестве полного предела один из односторонних:

Реально у этой функции в точке ноль только предел справа равен единице; а предел слева — нулю.

И последнее: почему я употребил в начале по отношению к функции limit() слово «полноценная». Потому что кроме нее существует еще одна «недофункция» — tlimit() ; она представляет собой фактически просто-напросто вызов самой функции limit() с поднятым флагом tlimswitch , то есть пытается при необходимости разложить «подпредельную» функцию в ряд Тейлора вне зависимости от реального значения этого флага. Другими словами вызов tlimit(аргументы) полностью аналогичен записи limit(аргументы) , tlimswitch:true ; только чуть короче. И аргументы она может принимать точно такие же.

Видео:Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать

…дифференцируем и интегрируем

О функции diff я кое-что уже рассказывал в первой статье, и здесь это «кое-что» только напомню. В двух упомянутых тогда вариантах вызова эта функция принимала один либо два аргумента. С двумя, diff(выражение, переменная) , она возвращает производную от «выражения» по заданной переменной; с одним, diff(выражение) — полный дифференциал заданного выражения. Другими словами, запись diff(f, x) равнозначна математическому обозначению d f /d x , а diff(f) — d f .

Но это еще не все. Кроме одного либо двух, эта функция может также принимать любое нечетное число агрументов вида diff(выражение, переменная, порядок, переменная, порядок, …) и возвращает при этом производную либо смешанную частную производную от выражения заданных порядков по заданным переменным. К примеру, diff(f, x, 3) означает d 3 f /d x 3 , а diff(f, x, 1, y, 2, z, 1) — d 4 f /d x d y 2 d z . Единственный флаг, имеющий прямое отношение к самой функции diff — это флаг derivabbrev, который влияет на отображение производных в ячейках вывода Maxima. По умолчанию он равен false , и производные обозначаются в виде дробей с буквой d; если же его выставить в true , производные будут отображаться в сокращенном виде, с переменными дифференцирования записанными в виде индексов:

Кроме того, функция diff используется еще и для обозначения производных в дифференциальных уравнениях. Но об этом чуть позже, а сейчас перейдем к интегрированию.

Основная функция интегрирования называется, как я уже говорил, integrate и имеет два варианта вызова: для нахождения неопределенного и определенного интегралов. Первый выглядит как integrate(выражение, переменная) , второй — как integrate(выражение, переменная, нижний-предел, верхний-предел) :

Вы, наверное, обратили внимание еще на один момент в ячейках %i4 – %o4 . Когда в выражении используется какой-либо независимый символ, результат, вообще говоря, может зависеть от значения этого символа. Если при этом о возможных значениях символа ничего не известно, то Maxima задаст вам один или несколько вопросов об этом значении, и решение будет искать в зависимости от ваших ответов на них. Так, в этом примере значение определенного интеграла напрямую зависит от знака параметра a:

Кроме обычных определенных интегралов Maxima умеет искать также и несобственные интегралы, то есть такие, у которых неограничена либо область интегрирования, либо подынтегральная функция; и делается это все той же функцией integrate :

В случае, если искомый интеграл не сходится, будет выдано сообщение об ошибке, говорящее о том, что интеграл расходящийся:

В случае, если интеграл не может быть найден, он либо целиком возвращается в несовершенном виде, либо упрощается частично и на выходе получается некоторая формула, включающая в несовершенном виде интеграл той части подынтегрального выражения, которую проинтегрировать не удалось:

Кроме функций diff и integrate , в Maxima есть еще много разнообразных возможностей, связанных с производными и интегралами, в частности, функции для численного расчета значений определенных интегралов, а также инструменты, применимые при работе с дифференциальными и интегральными уравнениями. И разнообразны они настолько, что для того, чтобы рассмотреть подробно и с примерами их все, не хватило бы всего этого цикла. А более тезисно, хотя и на английском языке, они описаны в документации. Посему с этой темой на этом прекращаем и движемся дальше.

Видео:10 класс, 31 урок, Методы решения тригонометрических уравнений (продолжение)Скачать

Решайте, сударь!

А дальше мы рассмотрим уравнения и их системы, и даже не столько рассмотрим, сколько порешим… то есть, конечно, порешаем. Уравнения и системы уравнений решаются в Maxima тоже одной и той же функцией, и тоже уже вам слегка знакомой по первой статье: это функция solve . Но прежде чем рассмотреть ее подробнее, нужно сказать пару слов о списках, или векторах, в Maxima; поскольку именно в виде списков solve возвращает корни, да и принимает параметры в случае решения системы уравнений, а не одного уравнения.

Синтаксис списков в Maxima весьма прост; это перечисление элементов в квадратных скобках: [элемент1, элемент2, …, элементN] . Особенность — не в синтаксисе. Основное достоинство Maximaльных списков в том, что их элементами могут быть совершенно любые выражения: символы, арифметические выражения, вызовы функций, присвоения, уравнения, другие списки… Додумать можете сами. Поэтому списки и во встроенных функциях применяются достаточно широко. Функция solve в своем простейшем варианте, для решения одиночного уравнения, в качестве аргументов никаких списков, напомню, не принимает (а принимает либо уравнение и символ, относительно которого его надо решать, либо только уравнение, если символ в нем всего один). А вот в качестве результата она уже и в таком варианте возвращает список, состоящий из всех корней заданного уравнения:

Как видите, функция solve находит все комплексные корни уравнения, а не только действительные.

К элементу списка можно обратиться с помощью тех же квадратных скобок, указав в них номер элемента после имени списка. Напомню, что равенство, переданное в качестве дополнительного параметра функции ev, означает подстановку переменной в вычисляемое выражение. Вот так мы можем осуществить проверку решения, подставив корень из выданного списка в исходное уравнение:

Точно таким же образом можно обратиться и к любому другому элементу списка:

Вообще говоря, в качестве первого аргумента функции solve можно задавать не только уравнение, а вообще любое выражение. При этом «корни выражения» (не являющегося уравнением) ищутся в том самом смысле, в каком эта фраза понимается в математике: корни выражения — это те значения переменной, на которых выражение обращается в ноль. Возможность такой записи позволяет, к примеру, легко найти критические точки любой непрерывной функции (а заодно и вычислить значения функции в этих точках):

В этом примере есть еще два важных момента. Первый — функция %th() . Она, как видно из контекста, вызывается как %th(n) и возвращает n -ю с конца ячейку вывода. Это, так же как и обозначения % и _ , удобно, чтобы не обращать внимания на номера ячеек, и кроме того, применимо в командных файлах Maxima, которые могут загружаться в том числе и прямо из интерактивной сессии (с помощью функции load ) — и тогда просто заранее неизвестно, начиная с какой ячейки данный файл загружен. И второй момент: здесь проиллюстрировано, что в Maxima операция индексирования списка доступна не только по отношению к именам переменных, но и к вызовам функций; другими словами, если функция возвращает список значений, мы можем выбрать одно конкретное из них, написав его номер в квадратных скобках прямо после вызова функции.

Вернемся к функции solve . А именно, перейдем теперь к решению систем уравнений. Для этого существует такой вариант записи: solve([уравнение1, уравнение2, …], [переменная1, переменная2, …]) ; либо сокращенный, аналогично варианту для одиночного уравнения: если количество уравнений и количество неизвестных равны, список неизвестных можно не писать: solve([уравнение1, уравнение2 …]) (не забудьте квадратные скобки, иначе Maxima примет его за вариант с одним уравнением).

Здесь возвращается список из нескольких списков, каждый из которых соответствует одному решению системы. В качестве подстановок можно использовать как такие списки целиком (например, в данном контексте, %o1[1] ), так и отдельные их элементы (например, %o1[1][1] ).

В случае, когда уравнений меньше, чем неизвестных, solve поступит точно так же, как и в случае одного уравнения с несколькими символами: все неуказанные будет воспринимать как параметры:

Если solve не находит точных решений, она может, как и integrate , вернуть уравнение или систему уравнений в некотором упрощенном виде, а может и самостоятельно попытаться решить систему численно:

В таком случае, если вам все же нужны точные значения корней (в аналитической записи), либо если они не найдены даже в числах, можно попробовать решить уравнения по очереди, выражая одно неизвестное через другое:

И подставляя в оставшиеся уравнения:

Теперь можем подставить обратно — и найти значения второй неизвестной, например, для первого и последнего корней из последнего списка:

Функция solve имеет довольно большое количество различных переключателей, из которых может пригодиться в своем не-умолчательном значении в первую очередь один: solveradcan . Умолчание здесь равно false , а выставив этот флаг в true , мы заставим solve , помимо его умолчательного поведения, применять radcan — функцию по упрощению показательных, логарифмических и степенных (с рациональными степенями) функций. Это делает работу функции solve более медленной (потому по умолчанию этот режим и выключен), но в некоторых случаях может помочь разрешить проблемы, которые без этого ключа приведут к невозможности найти точное решение.

Видео:Как решать тригонометрические неравенства?Скачать

И снова дифференцируем и интегрируем

Помимо «просто» уравнений, Maxima позволяет также решать и обыкновенные дифференциальные уравнения первого и второго порядка. Функций, непосредственно занимающихся решением таких уравнений, существует две. Первая из них занимается поиском частных решений линейных дифференциальных уравнений и систем таких уравнений; зовут ее desolve , от слов differential equation solve. Эта функция принимает два аргумента, первый из которых — уравнение либо список уравнений, а второй — соответственно одна переменная или список переменных. Если не заданы значения функций и/или их производных в нуле, то в найденном решении они просто отображаются в виде f(0) или

задать эти значения позволяет функция atvalue(выражение, переменная = точка, значение) ; то есть, в данном случае atvalue(f(x), x=0, значение) или atvalue(‘diff(f(x)), x=0, значение) . Производные в уравнениях и системах, решаемых с помощью этой функции, должны быть записаны непременно в виде ‘diff(f(x), x) , а не просто ‘diff(f, x) , а сами функции, соответственно, тоже в виде f(x) , а не f — нужно продемонстрировать зависимость функции от ее аргумента.

И конечно же, точно так же как для обычных уравнений и систем, здесь мы тоже можем проверить решение с помощью подстановки, но только надо еще дополнительно задать принудительное вычисление производных, так как в уравнениях они фигурируют в несовершенной форме:

Вторая функция из этой группы называется ode2 и предназначена она для решения обыкновенных дифференциальных уравнений первого и второго порядка; ее название происходит от фразы ordinary differential equations of 1st or 2nd order. Пишется она так: ode2(уравнение, зависимая-переменная, независимая-переменная) . Здесь уже независимая переменная указывается в списке параметров функции явно, и потому обозначения вида y(x) не нужны: и функция, и переменная обозначаются просто одиночными буквами. Также в отличие от предыдущей функции, ode2 ищет не частное, а общее решение. Произвольная константа в решении уравнения первого порядка обозначена через %c ; в решении уравнения второго порядка таких констант, естественно, две, и обозначаются они как %k1 и %k2 .

В дополнение к функции ode2 существуют три функции для поиска частных решений на основе полученных общих. Иначе говоря, эти функции, получая конкретные условия относительно значения функции-решения в заданной точке, находят исходя из этих значений соответствующие им величины интегральных констант. Одна из этих функций предназначена для обработки решения дифференциального уравнения первого порядка. Она называется ic1 (i от initial value — начальное значение; c от constant — константа; 1 от 1 st order — первого порядка) и принимает три аргумента: первый — само решение, в том виде, в котором его находит функция ode2 ; второй — значение независимой переменной ( x -координаты), третий — значение функции (зависимой переменной, у ) при этом значении x и возвращает частное решение, проходящее через точку с заданными координатами ( x , y ):

И две функции работают с решениями уравнений второго порядка. Так как в общем решении уравнения второго порядка фигурируют две независимые константы, то эти функции задают уже по два условия для поиска частного решения. Первая функция выглядит как ic2(общее решение, x, функция-в-точке-x, производная-в-точке-x) . Расшифровка названия аналогична предыдущей функции. Действует тоже аналогично ей, а в качестве второго условия задает значение производной в той же заданной точке:

И последняя функция называется bc2 (b от boundary value — граничное значение; а дальше все как в предыдущей). Ее аргументы: первым, как и в двух остальных вариантах, идет само общее решение, возвращенное функцией ode2 ; после него идут две пары значений: x ₀, y ₀, x ₁, y ₁, задающие две точки, через которые должен проходить график функции-решения:

Касательно дифференциальных уравнений все этими функциями и заканчивается, никаких дополнительных ключей к ним не предназначено.

В следующий раз мы поговорим о средствах построения графиков функций и о средствах автоматизации: условных операторах, циклах и управляющих условиях, налагаемых на различные символы и выражения.

Вопросы о Maxima или этого сайта: Списки рассылки

📸 Видео

ОДУ в программе MaximaСкачать