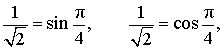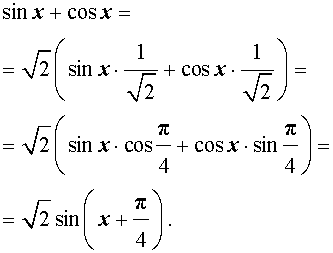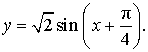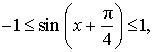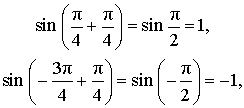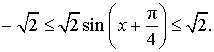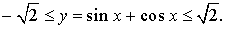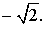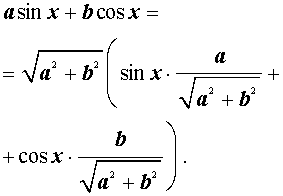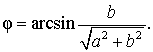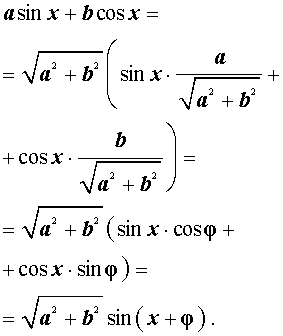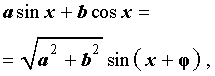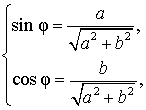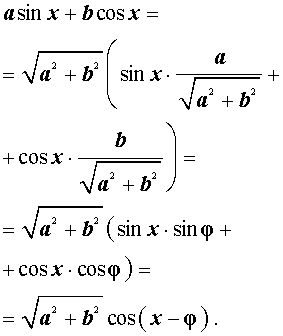Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.
ЗАДАЧА . Найти наибольшее и наименьшее значения функции
| y = sin x + cos x. | (1) |
РЕШЕНИЕ . Заметив, что
преобразуем правую часть формулы (1):
Отсюда вытекает, что выражение (1) можно переписать в виде:
ОТВЕТ . Наибольшее значение функции (1) равно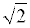 
, наименьшее значение функции (1) равно 
ЗАМЕЧАНИЕ . В рассмотренной задаче угол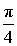 
и является дополнительным углом.
Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение
| a sin x + bcos x | (2) |
где a и b – произвольные, отличные от нуля числа, и преобразуем его:
Введем дополнительный угол (вспомогательный аргумент) φ , у которого:
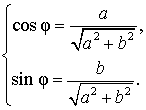 | (4) |
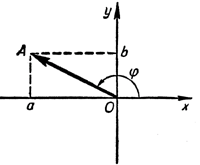
В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол
Тогда выражение (3) принимает вид:
Таким образом, мы получили формулу
которую и называют формулой дополнительного угла (вспомогательного аргумента).
Если же дополнительный угол, в отличие от формул (4), ввести по формулам
то выражение (3) примет вид
и мы получаем другой вид формулы дополнительного угла:
- Метод введения вспомогательного угла
- Преобразование выражения a sin х + b cos х путем введения вспомогательного угла
- Конспект урока по алгебре на тему «Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📹 Видео
Видео:ГРОБ в №13 на ЕГЭ 2021 по математике. Метод вспомогательного угла. Тригонометрия и ФСУСкачать
Метод введения вспомогательного угла
Видео:Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать
Преобразование выражения a sin х + b cos х путем введения вспомогательного угла
Лемма . Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.
Другими словами, если а 2 + b 2 = 1, то существует угол φ, такой, что
Прежде чем доказывать эту лемму, поясним ее на следующем примере:
Поэтому существует угол φ, такой, что ( frac ) = cos φ; 1 /2 = sin φ.
В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.
Рассмотрим вектор (vec) с координатами (а, b). Поскольку а 2 + b 2 = 1, длина этого вектора равна 1. Но в таком случае его координаты должны быть равны cos φ и sin φ, где φ — угол, который образует данный вектор с осью абсцисс.
Итак, а = cos φ; b =sin φ, что и требовалось доказать.
Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.
Прежде всего вынесем за скобки выражение (sqrt)
Но в таком случае
a sin х + b cos х = (sqrt)(cos φ sin х + sin φ cos х) = (sqrt) sin ( x + φ )
a sin х + b cos х = (sqrt) sin (x + φ) , где угол φ определяется из условий
1) ( sin x + cos x = sqrt2 (frac sin x + fraccos x) = sqrt2 (cosfracsin x + sinfraccos x ) =\= sqrt2(sinx + frac) )
Полученную формулу sin x + cos x = (sqrt2(sinx + frac))полезно запомнить.
2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,
$$ 3sinx — 4cosx = sqrt(frac<sqrt>sinx — frac<sqrt>cosx) =\= 5(sinxcdotfrac — cosxcdotfrac) = 5sin(x — phi), $$
где под φ можно подразумевать любой угол, удовлетворяющий условиям:
В частности, можно положить φ = arctg 4 /3. Тогда получим:
3 sin х — 4 cos x = 5 sin (x — arctg 4 /3).
Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
Конспект урока по алгебре на тему «Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
План-конспект урока по предмету
«Решение тригонометрических уравнений.
Метод введения вспомогательного аргумента»
Автор: Ишмухаметова Р.Р.
Конспект урока по теме
«Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»
1. Организационный момент.
Приветствие, создание позитивного эмоционального настроя.
( На уроке учащиеся будут работать в группах, поэтому нужно представить старших групп, рассказать о правилах работы в группе и о самооценке своей работы на уроке.).
У.: У нас сегодня будет с одной стороны обычный урок, т.к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему?
Ответ: открытый урок.
А вот и не угадали. Мы с вами будем решать почти весь урок только одно уравнение. Но об этом немного попозже.
А сейчас давайте вспомним методы решения тригонометрических уравнений.
Ответ: Метод замены переменной, метод разложения на множители вынесением за скобки, метод разложения на множители с помощью формул суммы и разности синусов и косинусов, т.е. преобразование суммы в произведение и решение уравнений с использованием однородности.
(на экране появляются тригонометрические уравнения, учащиеся называют способы решения уравнений и по мере называния способы появляются на экране, справа от столбца уравнений )
sin x + cos x = 0
Б. Метод разложения на множители
sin 5 x — sin x = 0
В. Метод преобразования суммы в произведение
4 sin 2 x — cos x = 1
Г. Метод однородных уравнений
sin 2 x -5 sinxcosx + 6 cos 2 x =0
Работа в группах: 2. 1. Решение задания на соответствие тригонометрических уравнений и методов решения.
Задание группам: соединить стрелочками метод решения и уравнение. Обсуждают в группах, а затем проверяем, спрашиваю например 1 группу, а остальные проверяют и обсуждаем решение.
Даю время 2 мин, на самооценку 1 задания. На экране появляются критерии самооценки:
2.2. Решение данных тригонометрических уравнений и проверка их на доске.
Задание: решить данные тригонометрические уравнения (каждая группа решает все уравнения, но внутри группы распределяют, кто какое будет решать уравнение). Затем каждая группа записать решение на доске и объяснить метод решения одного уравнения на выбор.
Даю время 2 мин на самооценку. На экране появляются критерии самооценки:
2 балл — за решенное уравнение, но с допущенной ошибкой;
1 балл — за недорешенное уравнение;
И плюс 1 балл за ответ у доски.
3. Открытие новых знаний.
3.1.Постановка проблемы: проблемная ситуация с затруднением
Вы смогли выполнить задание?
Почему это задание не получилось?
Мы с вами при решении уравнений чаще всего не сразу видели, какой это способ решения.
Что мы для этого делали?
Сейчас я каждой группе предложу свой метод решения этого уравнения, а вы попробуете, выполнив какие-либо преобразования решить уравнение и отметить решение уравнения на единичном тригонометрическом круге. Затем разберем решение на доске. Если вы не сможете догадаться какое преобразование нужно выполнить, вы можете взять подсказку. Подсказки будут платные. Стоят они 0,5 балла.
Пытаются выполнить задание
не знаем способа решения.
Выполняли какие-либо тригонометрические преобразования
Подсказки напечатаны на карточках и разложены на столе учителя. Метод решения и шпаргалки к этому методу решения уравнения определенного цвета.
3.2. .Обсуждение и решение проблемы по группам.
3.3.Обсуждение проблемы у доски.
Записывают решения на доске и объясняют. Сделать вывод о решении после каждого объяснения.
На экране появляются 5 единичных тригонометрических круга, на которых отмечены решения уравнения.
3.4. Выводы и предложения по решению уравнения.
Почему такое произошло?
-Что мы делаем в этом случае? Как проверить кто прав?
Как выполняется проверка?
4 ответа одинаковые, а один ответ — другой.
Допустили ошибку при решении
или возник посторонний корень при возведении в квадрат
подставить в уравнение и если получим верное равенство, значит, этот корень является решением уравнения.
У.: Давайте выполним проверку корней уравнения. Каждая группа проверит одно решение.
Раздать листы с заданием, какой корень проверить, а затем результат вывешиваем на доску и делаем вывод о достоверности решений.
Вывод: Значения х = 0 и 2П и х = П2 являются решениями уравнения, а значения х = П и х =3 П2 не являются решениями данного уравнения или это так называемые посторонние корни.
У.: почему они возникли и при решении каким способом?
О.: при возведении в квадрат.
У.: Как можно уточнить ответ уравнения или что можно исключить из множества всех действительных чисел?
При каких значениях n у нас получаются верные решения, а при каких – не верные или посторонние?
Ответ: при п четных — верные, а при п нечетных – неверные.
3.5.Введение нового метода решения данного типа уравнения.
Какой способ вам показался новым?
Действительно этот способ для вас новый.
Если назовут несколько способов, то сначала проанализировать какие способы применяли при решении этого уравнения, и только потом этот способ появится как новый.
Сначала обсудить вопрос об общем виде уравнения.
Как вы думаете как в общем виде можно записать уравнение, которое мы решали?
У кого какие идеи, гипотезы?
У кого какие мнения?
Откройте учебники и найдите параграф, где говорится о решении уравнений такого вида. Прочитайте его.
А теперь давайте попробуем составить алгоритм решения уравнений такого вида.
На экране появляется постепенно алгоритм решения уравнения.
a cos x + b sin x = c,
1) делим мы на 
2) Уравнение принимает вид
3) Вводим вспомогательный аргумент (угол), такой, что 
и 
Т.о. уравнение можно записать в виде
, а это простейшее тригонометрическое уравнение.
Запишите себе в тетрадь.
Чему равны а, в и с в нашем уравнении?
Как можно получить в нашем случае из а и в 
Нужно было решить уравнение sinx + cos x = 1.
Там где делили на
Варианты ответов, но нужно чтобы возник ответ
a cos x + b sin x = c,
делим мы на
= 
4. Закрепление изученного материала.
4.1.Работа с учебником по поиску подобных уравнений.
Найдите на с.189 номер с подобным типом уравнений и давайте выберем уравнения, которые будем решать
4.2.Решение найденных уравнений изученным методом.
Выбираем и решаем в зависимости от времени.(№ 625 1,3 или 4)
Ответы записывают на листах и вывешиваем на доску. Анализируем решение и ставим оценки.
5. Подведение итогов.
А как ее мы можем уточнить?
Что мы вводили? Посмотрите в учебнике, на доску.
Так как мы можем уточнить тему
После уточнения вывешиваю тему на доску.
И все таки какой метод из примененных вами вам больше всего понравился?
Как видим этот тип уравнений можно решать любым из данных методов, лишь бы он был вам понятен.
Решение тригонометрических уравнений
Молчание или неточная формулировка
Решение тригонометрических урав
нений. Метод введения вспомогательного аргумента (или угла)
Каждая группа с учетом набранных баллов оценивает свой вклад в работу на уроке.
Проставьте на листе оценки за работу на уроке.
6. Задание для внеаудиторной самостоятельной работы.(появляется на экране)
Прочитать §.36 п.2 и решить № 664.
На «3» — решить новым способом уравнения этого номера.
На «4» — решить 2 способами уравнения этого номера;
На «5» — решить всевозможными способами эти уравнения.
А теперь выразите свое отношение к уроку. Понравился он вам или нет, получили ли вы новые знания, или этот урок оставил вас равнодушными к математике.
Прикрепить к синусоиде (она вывешивается на доску) кружочки желтого, зеленого и коричневого цвета. Желтые крепятся сверху, коричневые – снизу синусоиды, а зеленые на ось Ох.
Посмотрите как мы сегодня поработали . Молодцы!
Спасибо за хорошую работу на уроке. До свидания.
Прочитать §36 п.2
На «3» — решить новым способом уравнения этого номера.
На «4» — решить 2 способами уравнения этого номера;
На «5» — решить всевозможными способами эти уравнения.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 314 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Однородные уравнения и метод вспомогательного аргумента. Тригонометрические уравнения Часть 4 из 6.Скачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 567 207 материалов в базе
Другие материалы
- 10.09.2018
- 223
- 0
- 10.09.2018
- 165
- 0
- 10.09.2018
- 5033
- 36
- 10.09.2018
- 279
- 2
- 10.09.2018
- 576
- 0
- 10.09.2018
- 1920
- 46
- 10.09.2018
- 304
- 2
- 10.09.2018
- 1066
- 3
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 10.09.2018 1426
- DOCX 113.5 кбайт
- 71 скачивание
- Оцените материал:
Настоящий материал опубликован пользователем Ишмухаметова Резеда Расуловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 8 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 1668
- Всего материалов: 2
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Решение тригонометрических уравнений методом вспомогательного углаСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📹 Видео
Метод введения вспомогательного аргумента. Видеоурок 34. Алгебра 10 классСкачать
Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать
Формулы половинного угла. 9 класс.Скачать
Как решать тригонометрические уравнения с помощью введения вспомогательного угла. Видеоурок #49Скачать
Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать
Формула дополнительного угла. Тригонометрия-17Скачать
Изи ЕГЭ. Математика. Задание 13: метод вспомогательного углаСкачать
12 часов Тригонометрии с 0.Скачать
Тригонометрические уравнения в ЕГЭ. Метод вспомогательного углаСкачать
Решение тригонометрических уравнений. 10 класс.Скачать
Метод дополнительного аргумента при решении тригонометрических уравненийСкачать
Метод вспомогательного аргумента решения тригонометрических уравнений Подготовка к ГВЭ11+ЕГЭ #89Скачать
Метод вспомогательного аргумента. Тригонометрия. ЕГЭ 13 ЗаданиеСкачать
Решение тригонометрических уравнений методом введения вспомогательного угла, 10 классСкачать
МЕТОД ВВЕДЕНИЯ ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.Скачать
