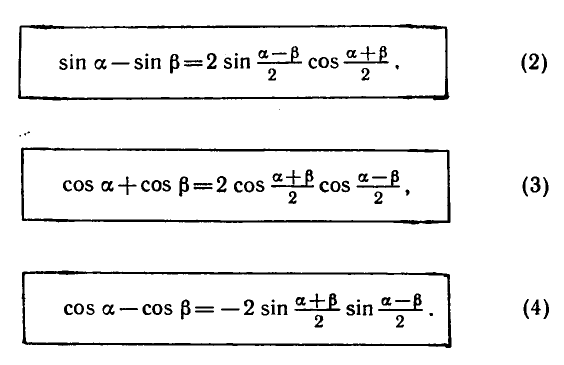
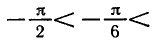
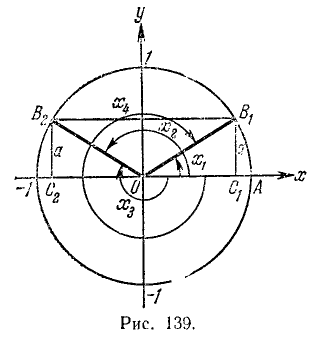
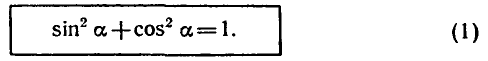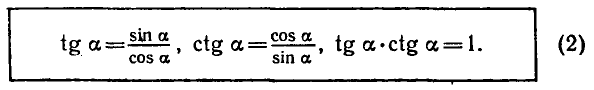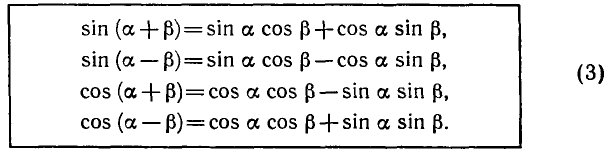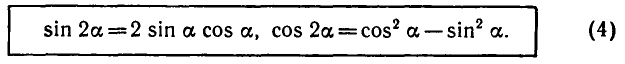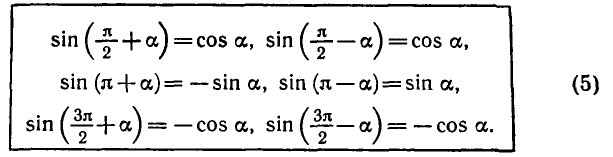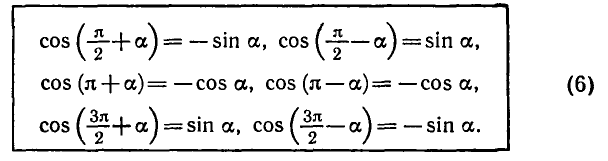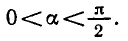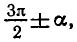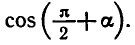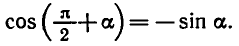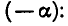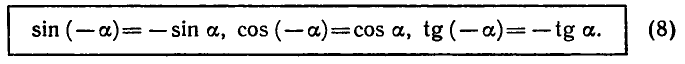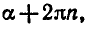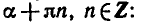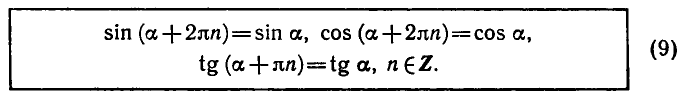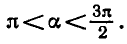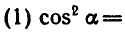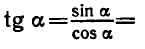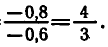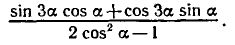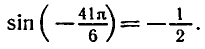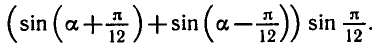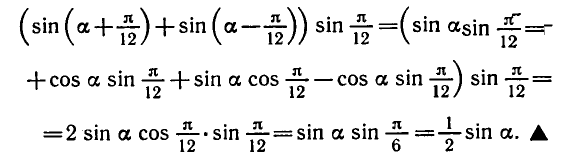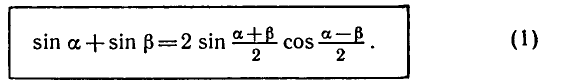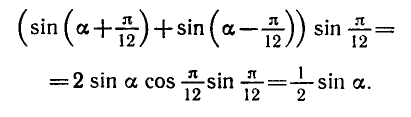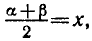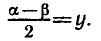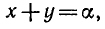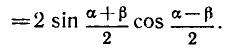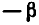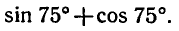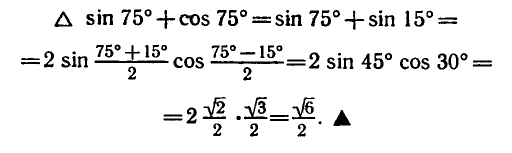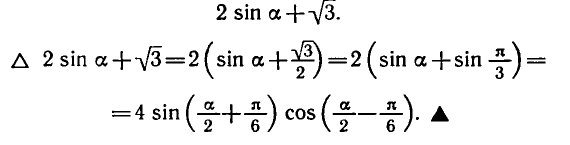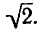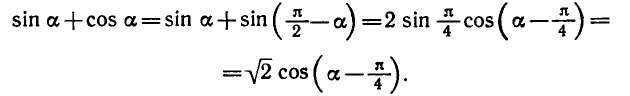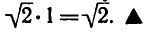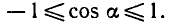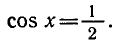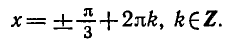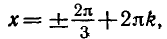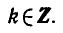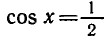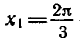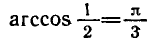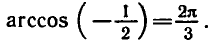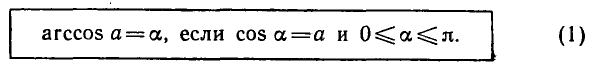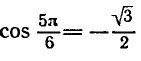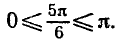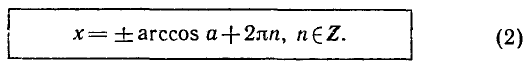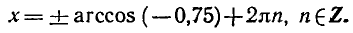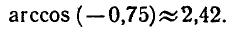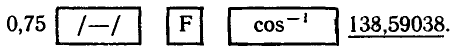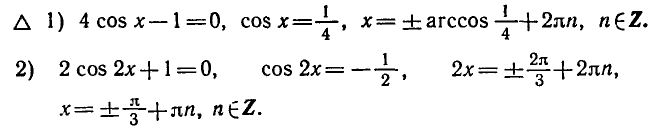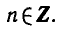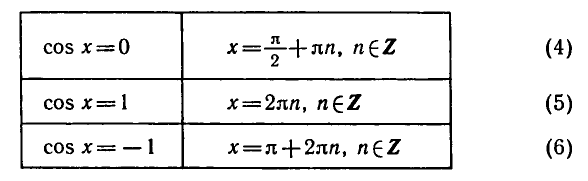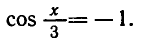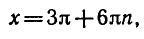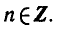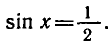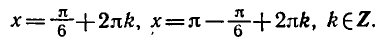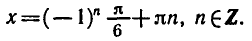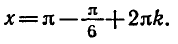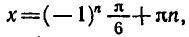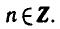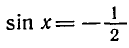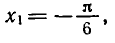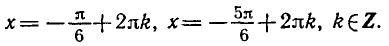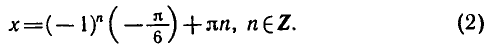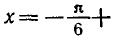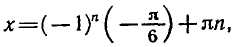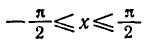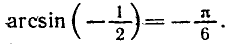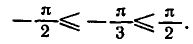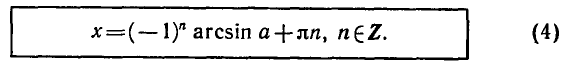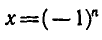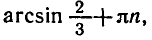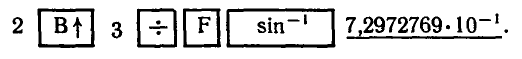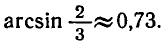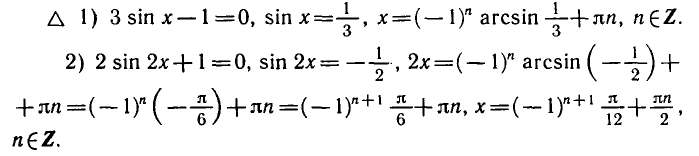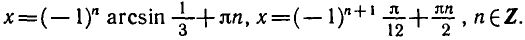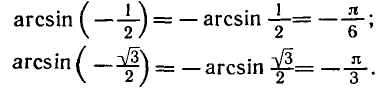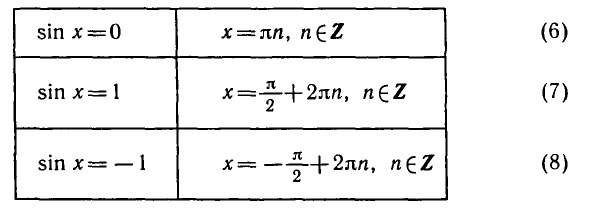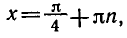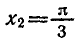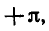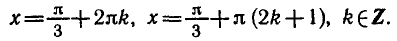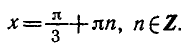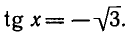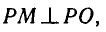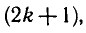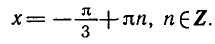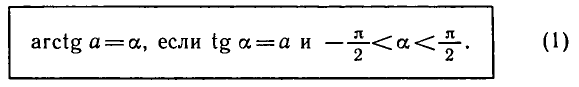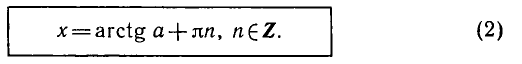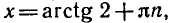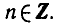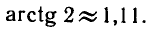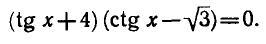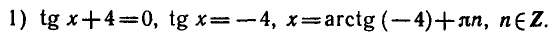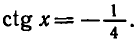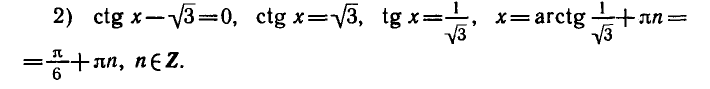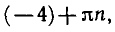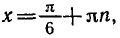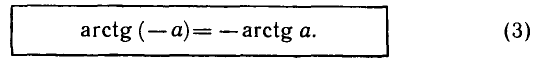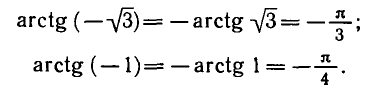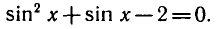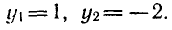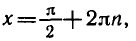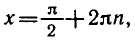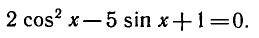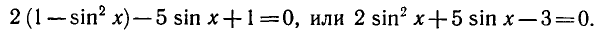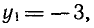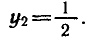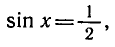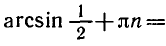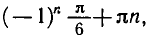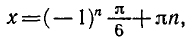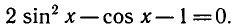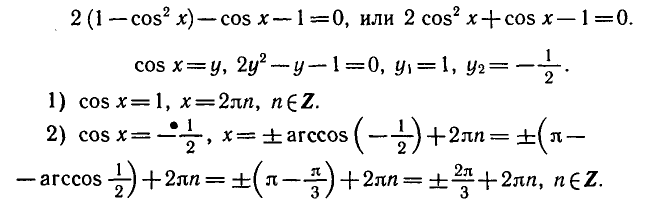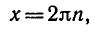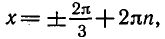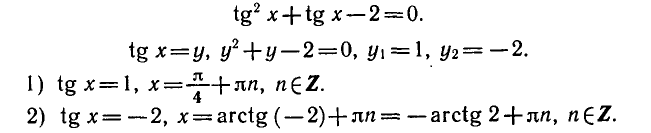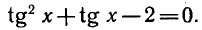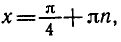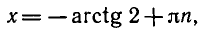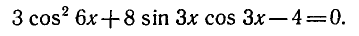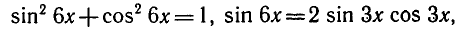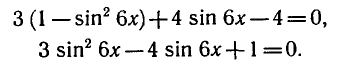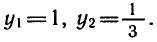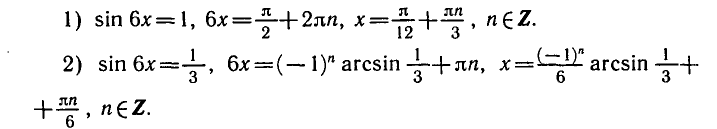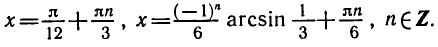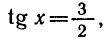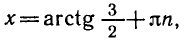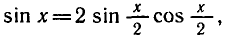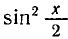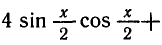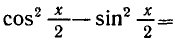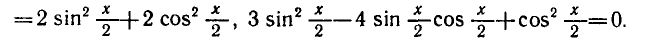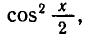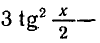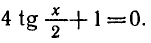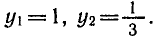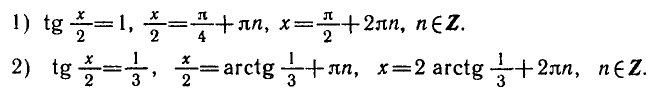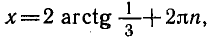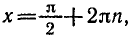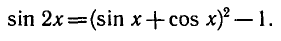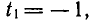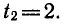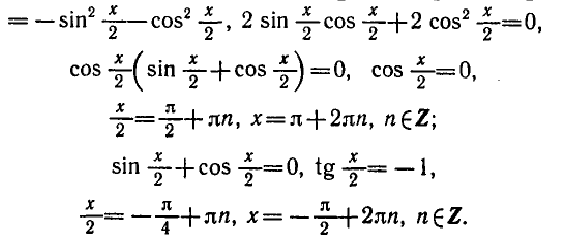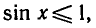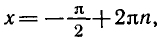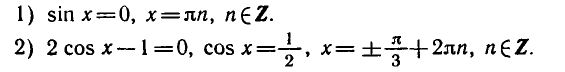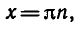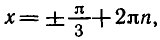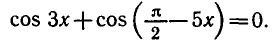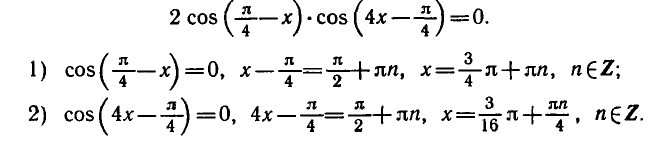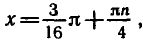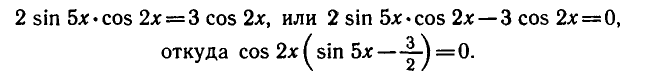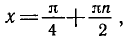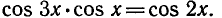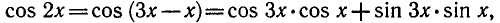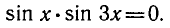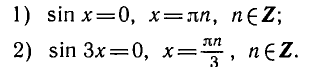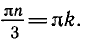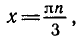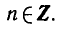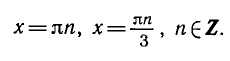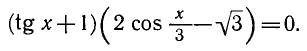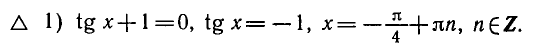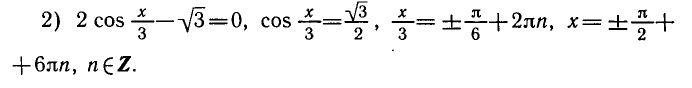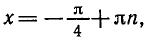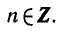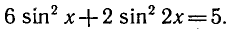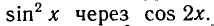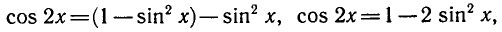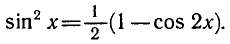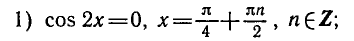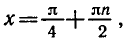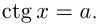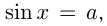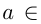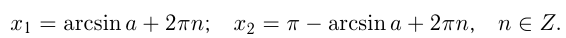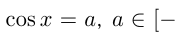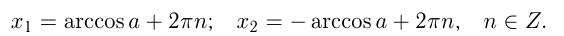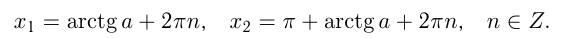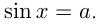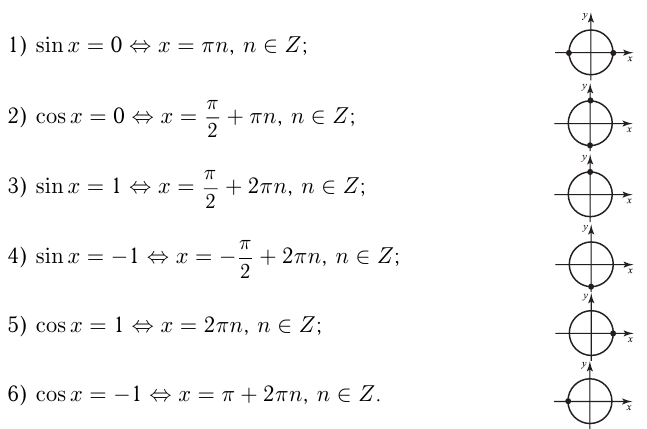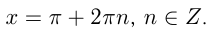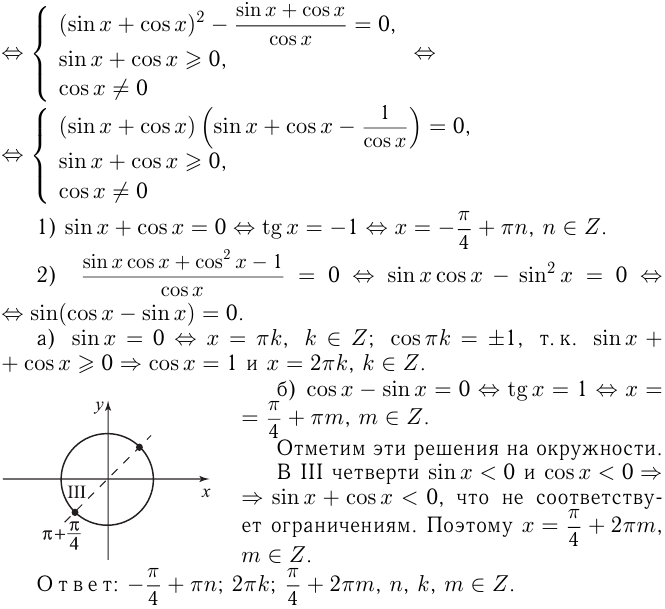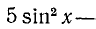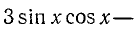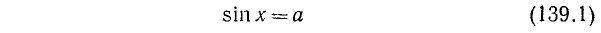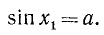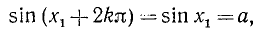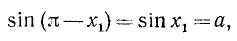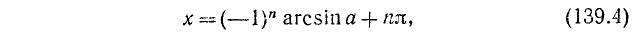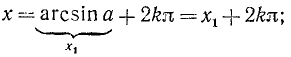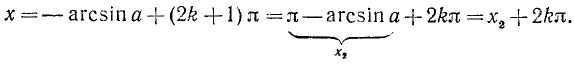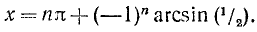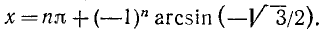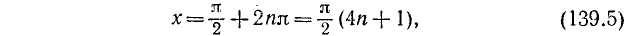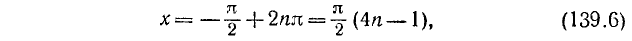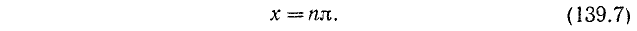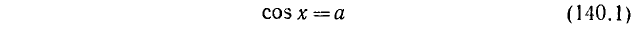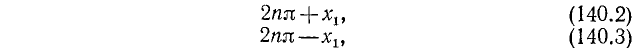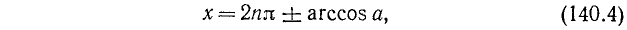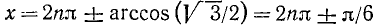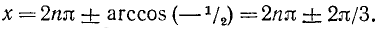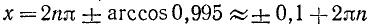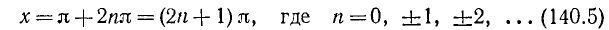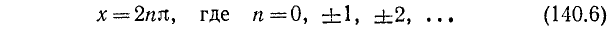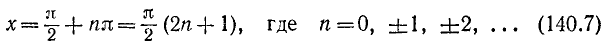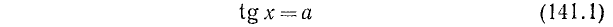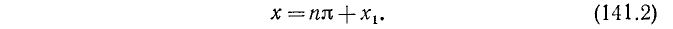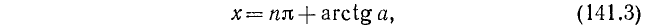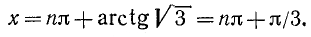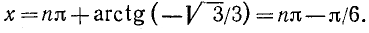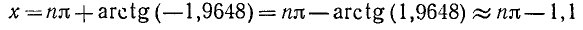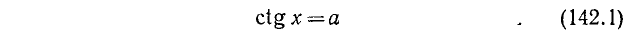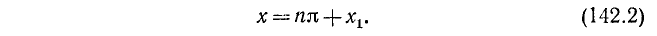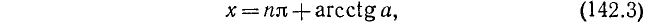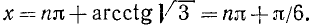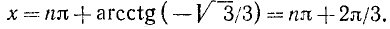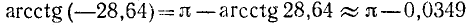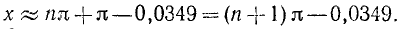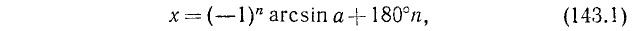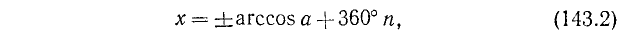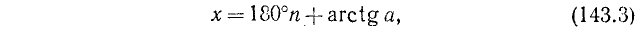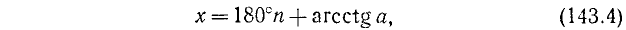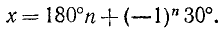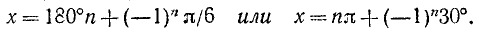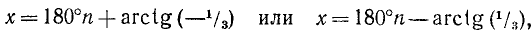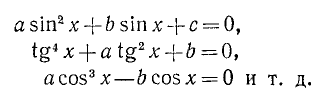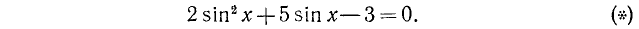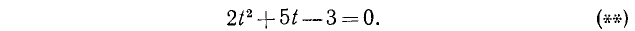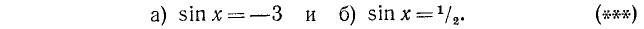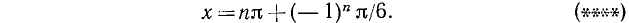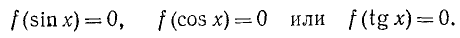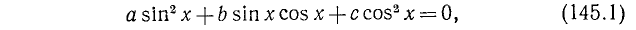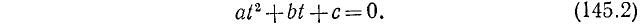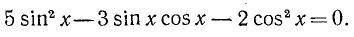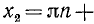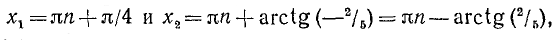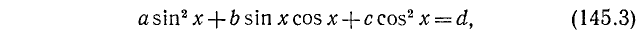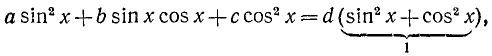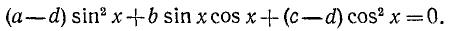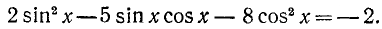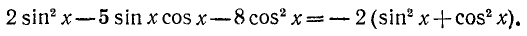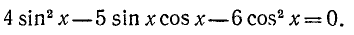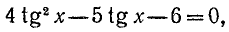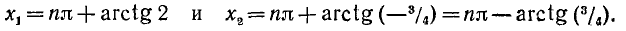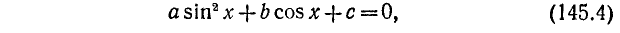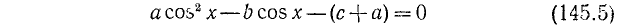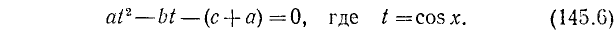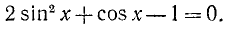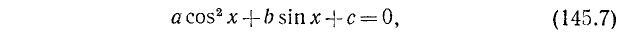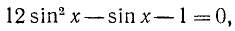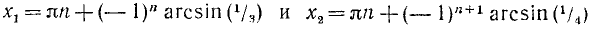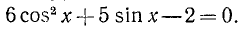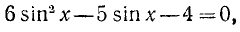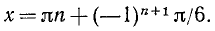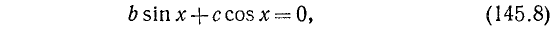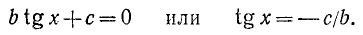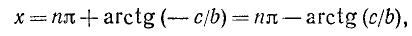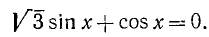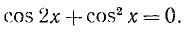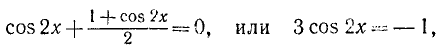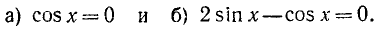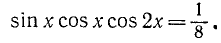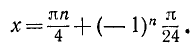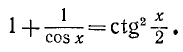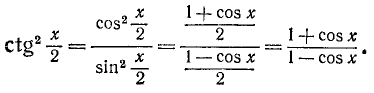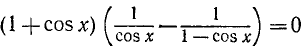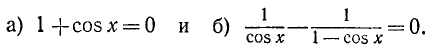Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
- Простейшие тригонометрические уравнения
- Формулы корней тригонометрических уравнений в таблице
- Методы решения тригонометрических уравнений
- Алгебраический метод.
- Разложение на множители.
- Приведение к однородному уравнению
- Переход к половинному углу
- Введение вспомогательного угла
- Дробно-рациональные тригонометрические уравнения
- Тригонометрические уравнения и неравенства с примерами решения и образцами выполнения
- Тригонометрические формулы
- Сумма и разность синусов. Сумма и разность косинусов
- Уравнение cos х = а
- Уравнение sin х= а
- Уравнение tg x = а
- Решение тригонометрических уравнений
- Уравнения, сводящиеся к квадратам
- Уравнения вида a sin х + b cos х = с
- Уравнения, решаемые разложением левой части на множители
- Тригонометрические уравнения и неравенства — основные понятия и определения
- Уравнения, разрешенные относительно одной из тригонометрических функций
- Уравнение sin х = а
- Уравнение cos x = a
- Уравнение tg x = a
- Уравнение ctg х = а
- Некоторые дополнения
- Способ приведения к одной функции одного и того же аргумента
- Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента
- Способ разложения на множители
- Решение тригонометрических уравнений с помощью формул приведения
- Методы решения тригонометрических уравнений.
- 1. Алгебраический метод.
- 2. Разложение на множители.
- 3. Приведение к однородному уравнению.
- 4. Переход к половинному углу.
- 5. Введение вспомогательного угла.
- 6. Преобразование произведения в сумму.
- 📺 Видео
Видео:Формулы приведения с нуля за 15 минут!Скачать

Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
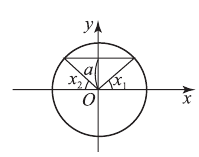
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| leq 1` имеет бесконечное множество решений.
Формула корней: `x=pm arccos a + 2pi n, n in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + pi n, n in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + pi n, n in Z`
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Формулы корней тригонометрических уравнений в таблице
Для синуса:


Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,
делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.
2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.
Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+pi n`, `n in Z`
- `tg x=1`, `x=arctg 1+pi n`, `x_2=pi/4+pi n`, ` n in Z`.
Ответ. `x_1=arctg (-2)+pi n`, `n in Z`, `x_2=pi/4+pi n`, `n in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2pi n`, `n in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Ответ. `x_1=2 arctg 2+2pi n, n in Z`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt `:
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `frac a<sqrt >=cos varphi`, ` frac b<sqrt > =sin varphi`, `frac c<sqrt >=C`, тогда:
`cos varphi sin x + sin varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt `, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos varphi` , `4/5=sin varphi`. Так как `sin varphi>0`, `cos varphi>0`, то в качестве вспомогательного угла возьмем `varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos varphi sin x+sin varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+varphi=(-1)^n arcsin 2/5+ pi n`, `n in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `frac =1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x ne 0`, `cos x ne -1`, ` x ne pi+2pi n, n in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=pi n`, `n in Z`
- `1-sin x=0`, `sin x=-1`, `x=pi /2+2pi n, n in Z`.
Учитывая, что ` x ne pi+2pi n, n in Z`, решениями будут `x=2pi n, n in Z` и `x=pi /2+2pi n`, `n in Z`.
Ответ. `x=2pi n`, `n in Z`, `x=pi /2+2pi n`, `n in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Видео:Формулы приведения - как их легко выучить!Скачать

Тригонометрические уравнения и неравенства с примерами решения и образцами выполнения
Корень уравнения есть число, которое, будучи подставленным в
уравнение вместо обозначающей его буквы или вида, приводит к
исчезновению всех его членов.
И. Ньютон
Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Тригонометрические формулы
В курсе алгебры рассматривались синус, косинус и тангенс
произвольного угла, выраженного в градусах или радианах.
Там же были доказаны основные формулы, которые
использовались для преобразований тригонометрических выражений.
Напомним эти формулы:
1. Основное тригонометрическое тождество:
2. Зависимость между синусом, косинусом, тангенсом и котангенсом:
Ньютон Исаак (1643— 1727) — английский математик, физик, механик, астроном; основоположник современной механики; одновременно с немецким математиком Г. Лейбницем ему принадлежит разработка дифференциального и интегрального исчислений.
3. Формулы сложения:
4. Формулы синуса и косинуса двойного угла:
5. Формулы приведения:
Формулы приведения запоминать необязательно. Для того
чтобы записать любую из них, можно руководствоваться
следующими правилами:
1) В правой части формулы который
2) Если в левой части формулы угол равен 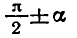
то синус заменяется на косинус, тангенс —
на котангенс и наоборот. Если угол равен 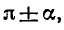
не происходит.
Например, покажем, как с помощью этих правил можно
получить формулу приведения для
По первому правилу в правой части формулы нужно поставить знак >,
так как если 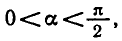
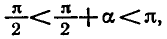
6. Формулы синуса, косинуса, тангенс угла
7. Формулы синуса и косинуса угла
тангенса угла
Приведем несколько примеров применения формул (1) — (9).
Пример:
Вычислить 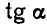
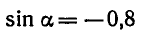
Сначала найдем 
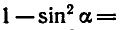
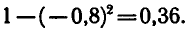
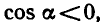
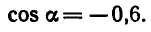
Пример:
Используя формулы (1), (3) и (4), получаем:
Пример:
Вычислить
Используя формулы (8) и (9), получаем:
По формулам приведения находим:
Ответ.
Сумма и разность синусов. Сумма и разность косинусов
Пример:
Используя формулу сложения и формулу синуса двойного
угла, получаем:
Эту задачу можно решить проще, если использовать формулу
суммы синусов:
С помощью этой формулы получаем:
Докажем теперь справедливость формулы (1).
Обозначим
Тогда 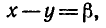
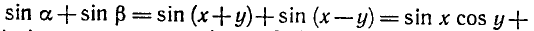
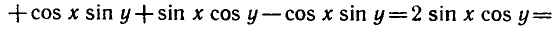
Наряду с формулой (1) используются формула разности
синусов, а также формулы суммы и разности косинусов:
Формулы (3) и (4) доказываются так же, как и формула (1);
формула (2 ) получается из формулы ( 1 ) заменой 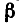
(докажите самостоятельно).
Пример:
Вычислить
Пример:
Преобразовать в произведение
Пример:
Доказать, что наименьшее значение выражения 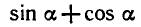
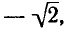
Преобразуем данное выражение в произведение:
Так как наименьшее значение косинуса равно — 1, а наибольшее равно 1, то наименьшее значение данного выражения
равно 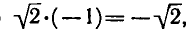
Уравнение cos х = а
Из курса алгебры известно, что значения косинуса заключены
в промежутке [— 1; 1], т. е.
Поэтому если |а |> 1 , то уравнение cos x = a не имеет корней. Например, уравнение cos x = — 1,5 не имеет корней.
Пример:
Решить уравнение
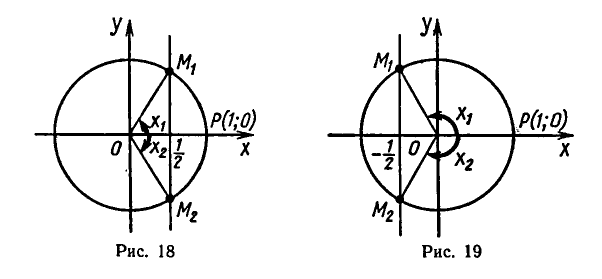
Напомним, что cos х — абсцисса точки единичной окружности, полученной поворотом точки Р (1; 0) вокруг начала координат на угол х. Абсциссу, равную имеют две точки окружности
и 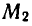
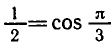
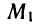
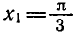
углы 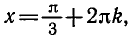
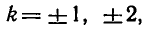
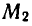
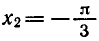
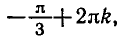
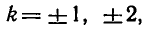
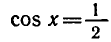
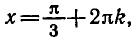
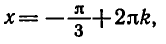
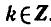
Пример:
Решить уравнение
Абсциссу, равную 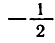
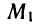
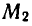
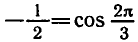
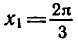
а потому угол 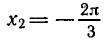
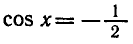
Таким образом, каждое из уравнений
и 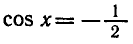
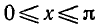
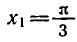
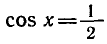
— корень уравнения 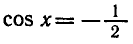
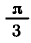
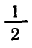
а число 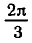
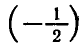
Вообще уравнение 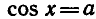

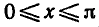
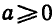
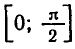
Например, 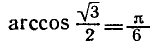
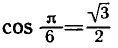
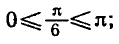
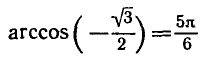
и
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что все корни уравнения 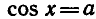
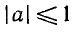
Пример:
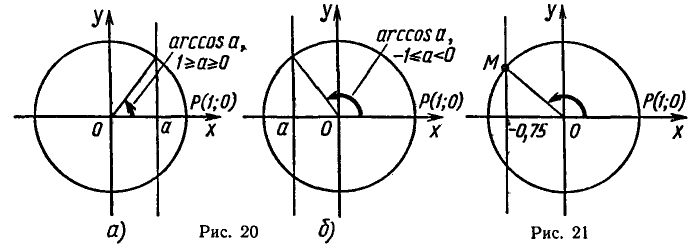
Решить уравнение cos x = — 0,75.
По формуле (2) находим
Значение arccos ( — 0,75) можно приближенно найти на рисунке 21, измеряя угол РОМ транспортиром.
Приближенные значения арккосинуса можно также находить
с помощью специальных таблиц или микрокалькулятора. На
пример, значение arccos (—0,75) можно вычислить на
микрокалькуляторе МК-54 по программе
Итак,
В данном случае переключатель микрокалькулятора Р-ГРД-Г
был установлен в положение Р (радиан).
Если вычисления проводить в градусной мере, то переключатель микрокалькулятора Р-ГРД-Г следует установить в положение Г (градус). Программа вычислений остается прежней:
Итак, 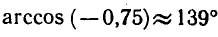
Пример:
Решить уравнение (4 cos х — 1) (2 cos 2x + 1)=0.
Ответ. 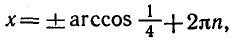
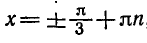
Можно доказать, что для любого 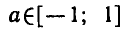
формула
Эта формула позволяет выражать значения арккосинусов
отрицательных чисел через значения арккосинусов
положительных чисел. Например:
Из формулы (2) следует, что корни уравнения cos х = а при а = 0,
а = 1, а = — 1 можно находить по более простым формулам:
Задача 5. Решить уравнение
По формуле (6) получаем 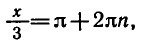
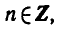
Уравнение sin х= а
Известно, что значения синуса заключены в промежутке
[— 1; 1], т. е. 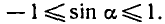
уравнение sin x = a не имеет корней. Например, уравнение
sin x = 2 не имеет корней.
Пример:
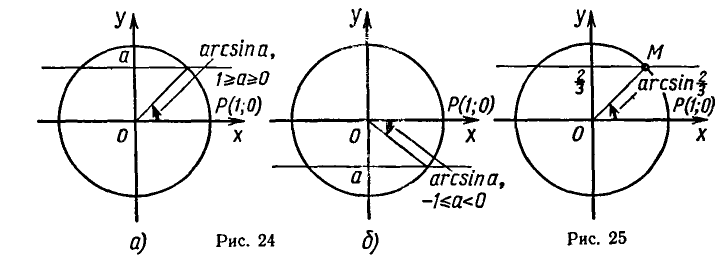
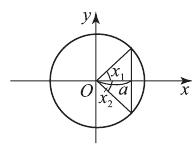
Решить уравнение
Напомним, что sin x — ордината точки единичной окружности, полученной поворотом точки Р (1; 0) вокруг начала координат на угол x. Ординату, равную 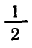
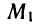
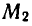
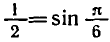
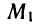
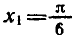
углы 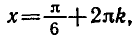
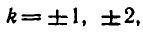
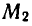
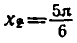
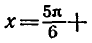
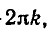
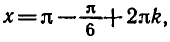
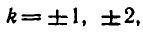
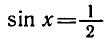
Эти формулы объединяются в одну:
В самом деле, если n — четное число, т. е. n = 2k, то из формулы (1) получаем 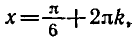
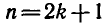
О т в е т .
Пример:
Решить уравнение
Ординату, равную 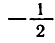
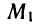
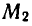
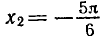
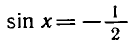
Эти формулы объединяются в одну:
В самом деле, если n = 2k, то по формуле (2) получаем 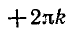
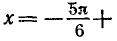
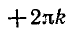
Ответ.
Итак, каждое из уравнений 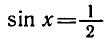
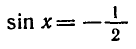
бесконечное множество корней. На отрезке
каждое из этих уравнений имеет только один корень: 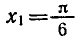
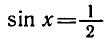
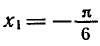
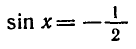
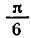
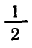
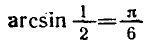
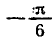
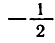
Вообще уравнение sin x = a, где 
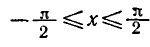
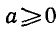
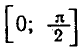
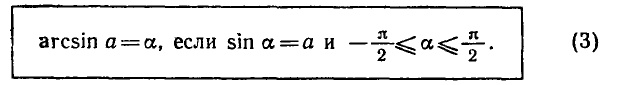
Например, 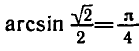
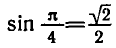
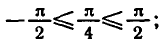
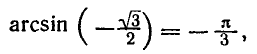
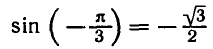
Аналогично тому, как это сделано при решении задач 1 и 2 можно показать, что корни уравнения sin x = a, где 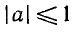
Пример:
Решить уравнение 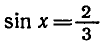
По формуле (4) находим
Значение 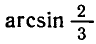
измеряя угол РОМ транспортиром.
Значения арксинуса можно находить с помощью специальных
таблиц или с помощью микрокалькулятора. Например, значение 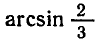
программе
Итак,
При этом переключатель микрокалькулятора Р-ГРД-Г был установлен в положение Р (радиан).
Пример:
Решить уравнение (3 sin х — 1) (2 sin 2х + 1) = 0.
Можно доказать, что для любого 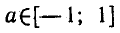
формула
Эта формула позволяет находить значения арксинусов отри
цательных чисел через значения арксинусов положительных
чисел. Например:
Отметим, что из формулы (4) следует, что корни уравнения
sin x = a при а = 0 , а = 1 , а = — 1 можно находить по более
простым формулам:
Пример:
Решить уравнение sin 2х = 1.
По формуле (7) имеем 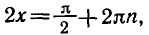
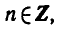
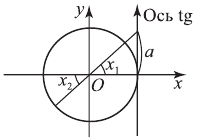
Уравнение tg x = а
Известно, что тангенс может принимать любое действительное
значение. Поэтому уравнение tg x = a имеет корни при любом
значении а.
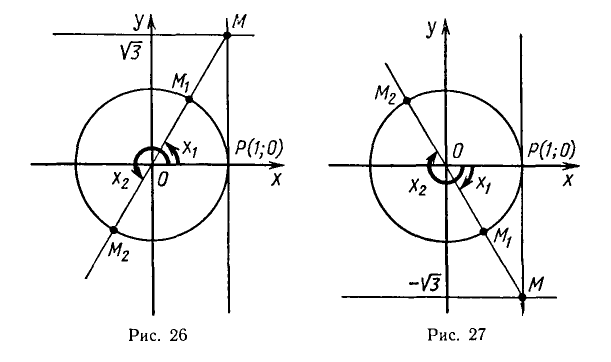
Пример:
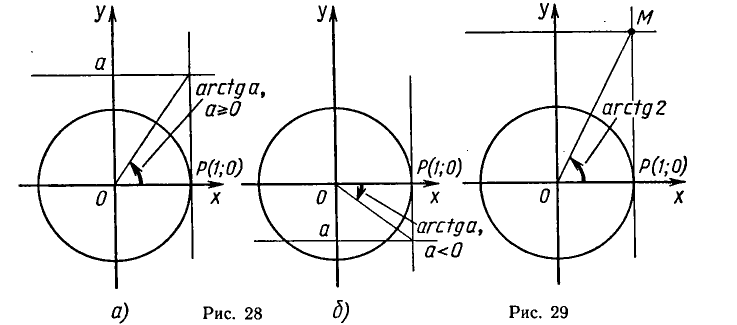
Решить уравнение
Построим углы, тангенсы которых равны 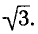
и отложим отрезок 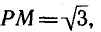
мую. Эта прямая пересекает единичную окружность в двух диа
метрально противоположных точках 
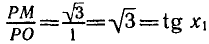
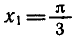
Таким образом, точка 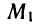
вокруг начала координат на угол а также на углы 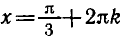
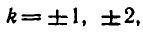
Точка 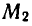
а также на углы 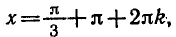
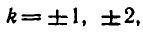
Итак, корни уравнения 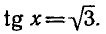
Эти формулы объединяются в одну
Пример:
Решить уравнение
Углы, тангенсы которых равны 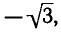
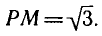
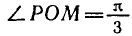

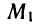
координат на угол 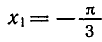
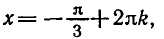
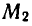
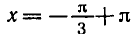
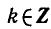
Поэтому корни уравнения 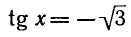
Итак, каждое из уравнений 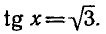
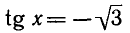
бесконечное множество корней. На интервале — каждое из этих уравнений имеет только один корень: 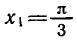
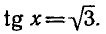
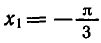
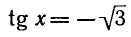
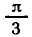
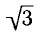
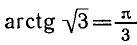
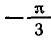
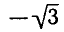
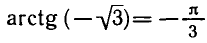
Вообще уравнение tg х = а для любого 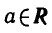
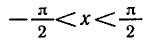
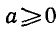
заключен в промежутке 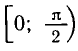
Например, 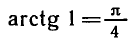
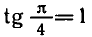
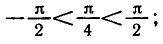
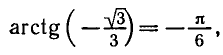
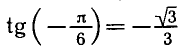
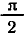
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что все корни уравнения tg x = a, где 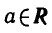
Пример:
Решить уравнение tg х = 2.
По формуле (2) находим
Значение arctg 2 можно приближенно найти из рисунка 29,
измеряя угол РОМ транспортиром.
Приближенные значения арктангенса можно также найти по
таблицам или с помощью микрокалькулятора.
Например, значение arctg 2 можно вычислить на МК-54 по
программе
Итак,
Пример:
При этих значениях х первая скобка левой части исходного
уравнения обращается в нуль, а вторая не теряет смысла, так
как из равенства tg x = — 4 следует, что
Следовательно, найденные значения х являются корнями исходного уравнения.
Эти значения x также являются корнями исходного уравнения, так как при этом вторая скобка левой части уравнения
равна нулю, а первая скобка не теряет смысла.
Ответ. 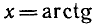
Можно доказать, что для любого 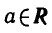
Эта формула позволяет выражать значения арктангенсов
отрицательных чисел через значения арктангенсов положительных чисел.
Например:
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Решение тригонометрических уравнений
Формулы корней простейших тригонометрических уравнений sin x = a, cos x = a, tg х = а. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение формул преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратам
Пример:
Решить уравнение
Это уравнение является квадратным относительно sin х.
Обозначив sin x= y, получим уравнение 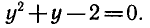
Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin х = 1 и sin х = — 2.
Уравнение sin x = l имеет корни 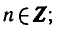
sin x = — 2 не имеет корней.
Ответ.
Пример:
Решить уравнение
Заменяя 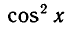
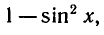
Обозначая sin х = у, получаем 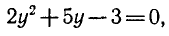
1) sin х = — 3 — уравнение не имеет корней, так как | — 3 | > 1.
2) 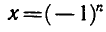
Ответ.
Пример:
Решить уравнение
Используя формулу 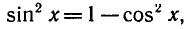
Ответ.
Пример:
Решить уравнение tg x — 2 ctg x + 1 = 0 .
Так как 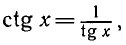
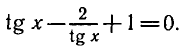
Умножая обе части уравнения на tg x, получаем:
Отметим, что левая часть исходного уравнения имеет смысл,
если 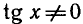
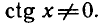
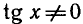
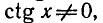
Ответ.
Пример:
Обозначив sin 6 x = у, получим уравнение 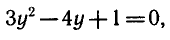
Уравнения вида a sin х + b cos х = с
Пример:
Решить уравнение 2 sin x —3 cos x = 0.
Поделив уравнение на cos x, получим 2tg x — 3 = 0,
При решении этой задачи обе части уравнения 2 sin x — cos x = 0 были поделены на cos x. Напомним, что при делении
уравнения на выражение, содержащее неизвестное, могут быть
потеряны корни. Поэтому нужно проверить, не являются ли
корни уравнения cos x = 0 корнями данного уравнения. Если
cos x = 0, то из уравнения 2 sin x — cos x = 0 следует, что sin x = 0. Однако sin х и cos х не могут одновременно равняться нулю, так как они связаны равенством 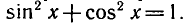
делении уравнения a sin х + b cos x = 0, где 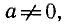
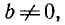
(или sin x) корни этого уравнения не теряются.
Пример:
Решить уравнение 2 sin x + cos x = 2.
Используя формулы 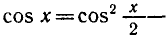
и записывая правую часть уравнения в виде 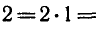
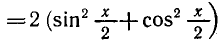
Поделив это уравнение на
Обозначая 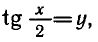
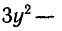
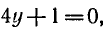
Ответ.
Пример:
Решить уравнение sin 2x — sin x — cos x — 1 = 0.
Выразим sin 2 x через sin x + cos x , используя тождество
Обозначим sin x + cos x = t, тогда 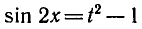
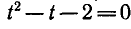
2) Уравнение sin x + cos x = 2 не имеет корней, так как
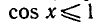
выполняться.
Ответ. 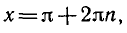
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на
множители.
Пример:
Решить уравнение sin 2х — sin х = 0.
Используя формулу для синуса двойного аргумента, запишем уравнение в виде 2 sin х cos х — sin х = 0.
Вынося общий множитель sin х за скобки, получаем
sin x (2 cos x — 1) = 0
Ответ.
Пример:
Решить уравнение cos Зх + sin 5x = 0.
Используя формулу приведения 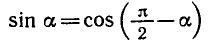
Используя формулу для суммы косинусов, получаем:
Ответ. 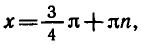
Пример:
Решить уравнение sin 7 x + sin 3 х = 3 cos 2х.
Применяя формулу для суммы синусов, запишем уравнение в виде
Уравнение cos2x = 0 имеет корни 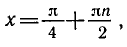
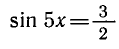
Ответ.
Пример:
Решить уравнение
уравнение примет вид:
Заметим, что числа вида содержатся среди чисел вида 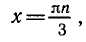
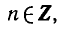
Следовательно, первая серия корней содержится во второй.
Ответ.
Часто бывает трудно усмотреть, что две серии корней, полу
ченных при решении тригонометрического уравнения, имеют об
щую часть. В этих случаях ответ можно оставлять в виде двух
серий. Например, ответ к задаче 12 можно было записать и так:
Пример:
Эти значения х являются корнями исходного уравнения, так
как при этом первая скобка левой части уравнения равна нулю,
а вторая не теряет смысла.
При этих значениях х вторая скобка левой части исходного
уравнения равна нулю, а первая скобка не имеет смысла. Поэтому
эти значения не являются корнями исходного уравнения.
Ответ.
Пример:
Решить уравнение
Выразим
Так как 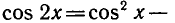
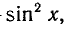
откуда
Поэтому исходное уравнение можно записать так:
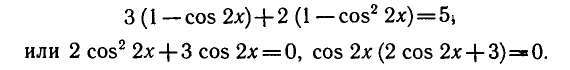
2) уравнение 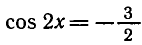
Ответ.
Решение тригонометрического уравнения состоит из двух частей: 1) преобразование тригонометрического выражения к простейшему виду; 2) решение простейшего тригонометрического уравнения. Первая часть сложна из-за множества применяемых формул как тригонометрических, так и алгебраических. Применяются такие приемы как разложение на множители, преобразование суммы или разности тригонометрических функций в произведение и, наоборот, произведения в сумму. Достаточно часто тригонометрические уравнения сводятся к линейным и квадратным уравнениям и уравнениям с корнями. Тригонометрические уравнения во всяком случае имеют ограничения, содержащиеся в тангенсе и котангенсе, т.к. 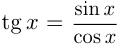
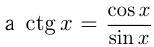
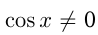
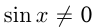
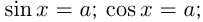
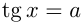
1) Решение уравнения 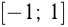
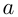
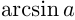
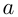
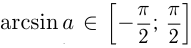
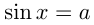
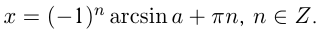
Напоминаем, что ось 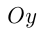
отмечается на оси 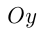
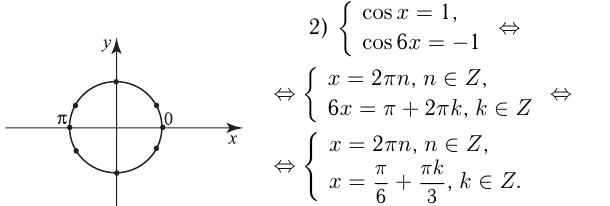
2) Решение уравнения 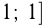
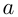
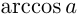
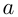
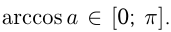
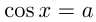
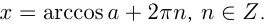
Эти решения отмечены на окружности.
Напоминаем, что ось 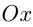
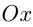
3) Решение уравнения 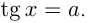
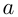
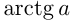
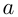
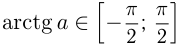
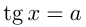
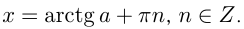
Напоминаем, что значение тангенса отмечается на оси тангенсов, которая параллельна оси 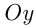
Там, где возможно, 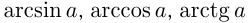
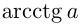
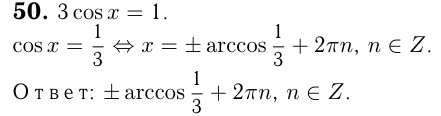
Здесь использована специальная формула, отличная от стандартной для уравнения
Существуют следующие специальные формулы:
Следует заметить также, что буква для обозначения целого числа может быть выбрана любая, но принято брать 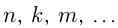
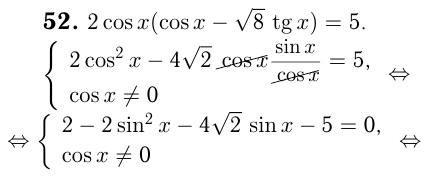
Т.к. решения 1-го и 2-го уравнений должны совпадать, то, как видно на окружности, единственно возможная точка соответствует решению
Эта система, как видно на окружности, решений не имеет
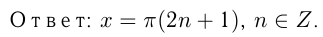

Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
Видео:Решение тригонометрических уравнений с помощью формул приведения. Часть 13.4Скачать

Тригонометрические уравнения и неравенства — основные понятия и определения
В этой главе мы рассмотрим некоторые уравнения, а также простейшие системы уравнений, содержащие неизвестную иод знаком тригонометрических функций. Такие уравнения называются тригонометрическими уравнениями.
Приведем некоторые примеры тригонометрических уравнений и их систем:
1) 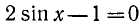
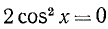
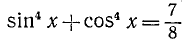
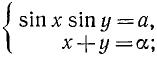
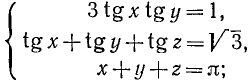
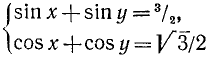
Решение различных типов тригонометрических уравнений большей частью основано на сведении их к некоторым простейшим уравнениям, которые мы рассмотрим ниже. При этом остаются в силе общие правила, относящиеся к решению уравнений. В частности, данное уравнение не всегда приводится к простейшей форме с помощью одних лишь равносильных преобразований. Поэтому следует проверить найденные решения, подставляя их в исходное уравнение.
Тригонометрические уравнения слишком разнообразны для того, чтобы пытаться дать их общую классификацию или общий метод решения. Мы можем указать лишь способы решения некоторых типов таких уравнений.
Уравнения, разрешенные относительно одной из тригонометрических функций
При решении различных тригонометрических уравнений мы будем часто приходить к некоторым простейшим уравнениям, решения которых следует запомнить. Приведем эти уравнения. Для того чтобы можно было дать геометрическую иллюстрацию к этим уравнениям, будем считать х углом в радианной мере.
Уравнение sin х = а
имеет решение при 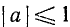
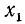
Тогда, в силу периодичности функции sin х, имеем
т.е. и числа вида 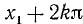
т. е. 
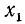
где k= 0, ±1, ±2, …
В качестве 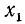
Объединив две серии (139.2) и (139.3) корней данного уравнения sin х = а одной формулой, мы будем записывать в дальнейшем его общее решение (совокупность всех корней) в виде
где n = 0, ±1, ±2, … и 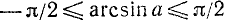
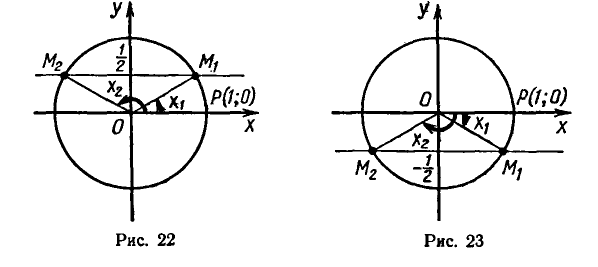
Поясним формулу (139.4) и другим способом, с помощью рис. 139.
Известно, что sin x = а (на рис. 139 ОA = 1, 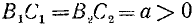
Уравнению (139.1) удовлетворят углы:
а) положительные: 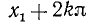
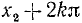
б) отрицательные: 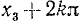
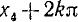
Все эти углы можно задать одной формулой (139.4), и, обратно, любой угол, полученный по формуле (139.4), есть угол либо вида а), либо вида б). Проверим, например, обратное утверждение для положительных углов.
Если 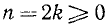
если же 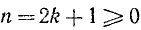
Аналогично проводится проверка и для отрицательных углов.
Пример:
sin x = 1/2.
Решение:
Так как 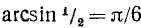
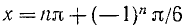
Пример:
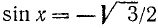
Решение:
Так как 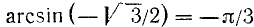
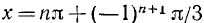
Замечание. При выводе формулы (139.4) мы воспользовались рис. 127, на котором 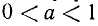
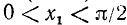
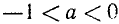
Допустим, что а = 1 или a = — 1. Корни уравнения sin х = 1 можно записать так:
где n = 0, ±1, ±2, …, а корни уравнения sin x = — 1 можно записать так:
где n = 0, ±1, ±2…. . Допустим теперь, что а = 0. Корни уравнения sin x = 0 можно записать так:
Уравнение cos x = a
имеет решение при 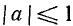
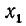
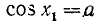
Тогда в силу периодичности 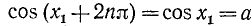
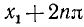

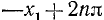
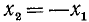
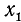
где n = 0, ±1, ±2, …
В качестве 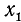
Объединив две серии (140.2) и (140.3) корней уравнения cos x = a одной формулой, мы будем писать в дальнейшем его общее решение (совокупность всех корней) в виде
где n = 0, ±1, ±2, … и 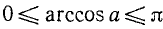
Рекомендуем читателю пояснить формулу (140.4) с помощью рисунка, аналогичного рис. 139.
Пример:
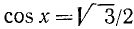
Решение:
Пример:
cos x = — х/2.
Решение:
Пример:
cos х = 0,995.
Решение:
(см. приложение II).
Замечание. При выводе формулы (140.4) мы воспользовались рис. 128, на котором 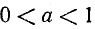
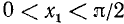
Уравнение cos x = l имеет корни:
Уравнение cos x = 0 имеет корни:
Уравнение tg x = a
имеет решение при любом а (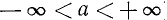
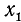
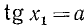
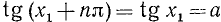
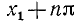
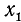
В качестве 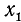
где n = 0, ±1, ±2, … и 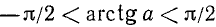
Пример:
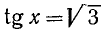
Решение:
Пример:
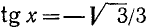
Решение:
Пример:
tg x = —1,9648.
Решение:
(см. приложение II).
Уравнение ctg х = а
имеет решение при любом а (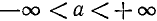
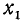
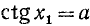
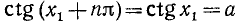
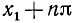
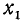
В качестве 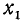
где n = 0, ±1, ±2, … и 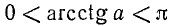
Пример:
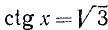
Решение:
Пример:
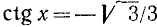
Решение:
Пример:
ctg х = —28,64.
Решение:
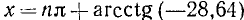
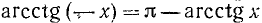
(см. приложение I). Следовательно,
Некоторые дополнения
Если в уравнениях sin x = a, cos х = а, tg х = а и ctg x = a известно, что х — угол в градусной мере, то общие решения нужно записывать по-другому.
Для уравнения sin x = a, где 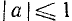
где n = 0, ±1, ±2, … и 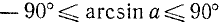
Для уравнения cos х = а, где 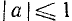
где n = 0, ±1, ±2, … и 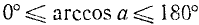
Для уравнения tg х = а, где а — любое число, нужно писать:
где n = 0, ±1, ±2, … и — 90°
где n = 0, ±1, ±2. … и 0°
б) Нельзя, однако, писать
Разберем примеры уравнений, непосредственно сводящихся к уже рассмотренным.
Пример:
Решить уравнение 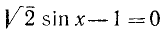
Решение:
sinх = 1 /]/2, откуда согласно (143.1) имеем х — 180°и + (—1)»45°, где я = 0, ±1, ±2, …
Пример:
Решить уравнение 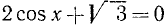
Решение:
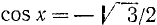
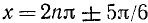
Пример:
Решить уравнение 3 sin х — 4 = 0.
Решение:
Из нашего уравнения получаем равносильное уравнение sin x = 4/3, которое решений не имеет, ибо не выполняется условие 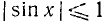
Пример:
Решить уравнение 3 tg х + 1 = 0.
Решение:
tg x = —1/3, откуда согласно (141.3) имеем 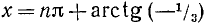
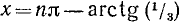
Замечание. Ответ можно записать так:
где n = 0, ±1, ±2, …
Пример:
Решить уравнение 3 ctg x + 2 = 0.
Решение:
ctg x = —2/3, откуда согласно (142.3) имеем 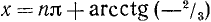
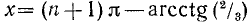
Пример:
Решить уравнение 2 sin 5x + l = 0.
Решение:
Записав уравнение в виде sin 5x = —1/2, найдем отсюда сначала промежуточный аргумент 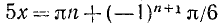
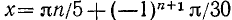
Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Способ приведения к одной функции одного и того же аргумента
Сущность способа: Мы получили решения уравнений вида sin x = a, cos х = а, tg x = a и cxg x = a. Во многих случаях решение тригонометрических уравнений сводится к решению основных элементарных уравнений после выполнения ряда алгебраических действий.
Так, пусть имеется уравнение, левая часть которого содержит х только под знаком одной тригонометрической функции, например:
Во всех этих случаях задача решения уравнения распадается на две:
1) Решение алгебраического уравнения относительно новой неизвестной t = sin x, t = tg x, t = cos x.
2) Решение уравнений вида sin x = a, cos x = a, tg x = a.
Пример:
Решение:
1) Положив sin x = t, приходим к алгебраическому уравнению (в данном случае к квадратному уравнению) относительно новой неизвестной t:
Решив уравнение 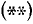
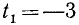
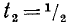
2) Задача решения уравнения 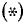
Уравнение sin x = — 3 решений не имеет. Общее решение уравнения sin x = 1/2 имеет вид
Так как при переходе от тригонометрического уравнения 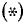
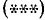
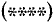
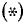
В большинстве случаев, однако, приходится исходное уравнение еще преобразовывать так, чтобы оно приобрело нужный вид:
В п. 145 показаны приемы таких преобразований.
Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента
1) Рассмотрим уравнение типа
где a, b и с — какие-то действительные числа. Изучим случай, когда 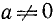
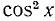
Заметим, что уравнения (145.1) и (145.2) будут равносильны, ибо мы предполагаем, что 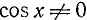
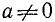
Пример:
Решение:
Разделим обе части уравнения на 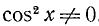
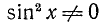
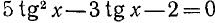
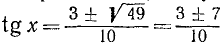
а) 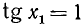
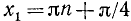
б) 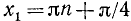
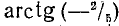
где п = 0, ±1, ±2, …
Замечание:
где 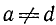
Пример:
Запишем данное уравнение так:
После этого будем иметь
Разделим обе части последнего уравнения на 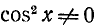
откуда 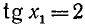
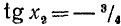
2) Рассмотрим уравнение типа
где a, b и с — какие-то действительные числа. Пусть 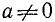
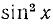
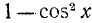
Из уравнения (145.6) находим возможные значения для t = соs x; естественно, что они будут иметь смысл лишь в случае 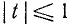
Решение. Заменяя 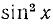
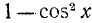
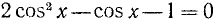
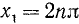
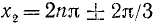
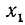
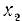
Пример:
Решение:
Заменив 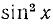
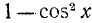
откуда cos x = 1/2 и cos x = —3/2. Последнее уравнение не имеет решений, ибо не выполнено условие 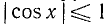
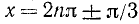
3) Рассмотрим уравнение тина
где a, b и с—какие-то действительные числа. Oграничимся рассмотрением примеров.
Пример:
Решение:
Заменив 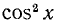
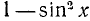
откуда sin x = 1/2 и sin x = —1/4. Оба последних уравнения имеют соответственно решения
Совокупность значений 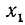
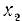
Пример:
Решение:
Заменив 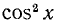
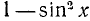
откуда 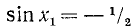

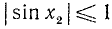
4) Рассмотрим уравнение типа
где 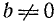
Деля обе части уравнения на 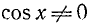
где n = 0, ±1, ±2, … Заметим, что, предположив 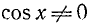
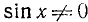
Пример:
Решение:
Разделим обе части уравнения на 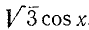
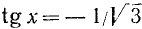
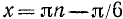
5) Если в уравнение входят тригонометрические функции от различных аргументов, то и в этом случае иногда представляется возможным выразить их все через одну тригонометрическую функцию одного и того же аргумента.
Пример:
Решение:
Заменив 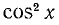
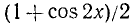
откуда cos 2х = — l/3.
Следовательно, 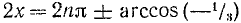
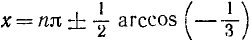
Пример:
Решить уравнение 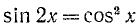
Решение:
Заменив sin 2x через 2sin x cos x, придем к уравнению 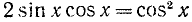
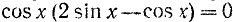
Первое уравнение имеет корни 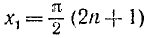
Второе уравнение после деления на 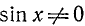
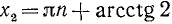
Решениями первоначального уравнения и будут значения 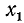
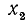
Пример:
Решение:
Умножим обе части уравнения на 2 и, заменив 2sin x cos x на sin 2х, получим sin 2x cos 2x = 1/4. С последним уравнением поступим опять так же, получим sin 4x = 1/2, откуда 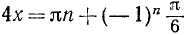
Пример:
Решение:
Подставив найденное значение для 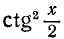
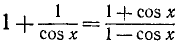
Последнее уравнение распадается на два:
Первое уравнение имеет корни 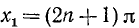
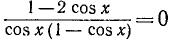
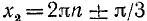
Способ разложения на множители
1) Если в уравнении, приведенном к виду f(x) = 0, его левая часть f(x) разлагается на множители, то, как указано в п. 54, следует приравнять каждый из этих множителей к нулю. Получится несколько отдельных уравнений; корни каждого из них будут корнями основного уравнения, если только они входят в о. д. з. каждого из множителей левой части уравнения.
Все полученные решения объединяются в одну совокупность решений первоначального уравнения. Заметим, что этот способ мы уже фактически применяли при решении примеров 9 и 11 из п. 145.
Рассмотрим е;це несколько примеров.
Пример:
Решить уравнение sin x ctg 2x = 0.
Решение:
Согласно предыдущему будем искать отдельно решения двух уравнений: a) sin x = 0 и б) ctg 2x = 0. Первое уравнение имеет корни 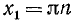
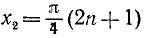
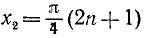
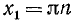
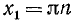
Видео:Решение тригонометрических уравнений. Метод понижения порядка. 10 класс.Скачать

Решение тригонометрических уравнений с помощью формул приведения
Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Методы решения тригонометрических уравнений.
Видео:Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

1. Алгебраический метод.
( метод замены переменной и подстановки ).
Видео:Как легко выучить ФОРМУЛЫ ПРИВЕДЕНИЯ // Тригонометрия, Подготовка к ЕГЭ по МатематикеСкачать

2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е . Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
Видео:12 часов Тригонометрии с 0.Скачать

3. Приведение к однородному уравнению.
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
cos ( или sin ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно tan .
П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда
1) tan x = –1, 2) tan x = –3,
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

4. Переход к половинному углу.
П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

5. Введение вспомогательного угла.
где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos 


Видео:Тригонометрия в ЕГЭ может быть простойСкачать

6. Преобразование произведения в сумму.
П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .
Р е ш е н и е . Преобразуем левую часть в сумму:
📺 Видео
ЕГЭ №9. Тригонометрические выражения.Тригонометрические уравнения | Математика | TutorOnlineСкачать

Тригонометрия. Повторяем основные формулы. Учимся их использовать. Вебинар | МатематикаСкачать

Решение тригонометрических уравнений. Вебинар | МатематикаСкачать

Решение тригонометрических уравнений. 10 класс.Скачать