Решение тригонометрических уравнений с двойным углом

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Примеры решения задач из ЕГЭ на формулы двойного угла

Вычислим (cos⁡frac) с помощью тригонометрического круга. Сначала найдем (frac) на круге:

Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.

Одинаковые синусы можно сократить.

Теперь обратите внимание на то, что (49^°=90^°-41^°).
Поэтому мы можем заменить (49^°) на (90^°-41^°).

((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс;

(90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos⁡ (90^°-41^°)=sin⁡41^°)

Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrtcos^2⁡frac-sqrt).

С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt).
(sqrt=sqrt=2sqrt).

Теперь можно вынести (sqrt) за скобки.

Вот теперь видно, что перед нами формула косинуса двойного угла.

Сокращаем (2) и (12).

Теперь применим к косинусу формулу приведения:

((π-frac)) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус;

(π) — находится на «горизонтали» — функция не меняется на кофункцию.

Видео:Тригонометрические уравнения двойных углов. Алгебра 10 классСкачать

Задача C1: тригонометрические уравнения и формула двойного угла

Очень часто в задачах C1 из ЕГЭ по математике ученикам предлагают решить тригонометрическое уравнение, содержащее формулу двойного угла.

Сегодня мы вновь будем разбирать задачу С1 и, в частности, разберем довольно нестандартный пример, который одновременно вместил в себе и формулу двойного угла, и даже однородное уравнение. Итак:

Решите уравнение. Найдите корни этого уравнения, принадлежащие промежутку:

sinx+ sin 2 x 2 − cos 2 x 2 ,x∈ [ −2 π ;− π 2 ]

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Полезные формулы для решения

Прежде всего, хотел бы напомнить, что все задания С1 решаются по одной и той же схеме. В первую очередь, исходную конструкцию нужно преобразовать в выражении, в котором содержится синус, косинус или тангенс:

Именно в этом состоит основная сложность задания С1. Дело в том, что для каждого конкретного выражения требуются свои выкладки, с помощью которых можно перейти от исходника к таким простейшим конструкциям. В нашем случае это формула двойного угла. Давайте я запишу ее:

cos2x= cos 2 x− sin 2 x

Однако в нашем задании нет cos 2 x <^>x или sin 2 x <^>x, зато есть sin 2 x 2 frac<<^>x> и cos 2 x 2 frac<<^>x>.

Видео:ДВОЙНЫЕ УГЛЫ И ФОРМУЛЫ ПРИВЕДЕНИЯ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Решаем задачу

Что же делать с этими выкладками? Давайте мы немножко схитрим, и в наши формулы синуса и косинуса двойного угла введем новую переменную:

Мы запишем такую конструкцию с синусом и косинусом:

cos2⋅ t 2 = cos 2 t 2 − sin 2 t 2

Или другими словами:

cost= cos 2 t 2 − sin 2 t 2

Возвращаемся к нашему исходному заданию. Давайте sin 2 x 2 frac<<^>x> перенесем вправо:

sinx= cos 2 x 2 − sin 2 x 2

Справа стоит именно те самые выкладки, которые мы только что записали. Давайте мы преобразуем их:

А теперь внимание: перед нами однородное тригонометрическое уравнение первой степени. Смотрите, у нас нет никаких слагаемых, состоящих просто из чисел и просто из x x, у нас есть только синус и косинус. Также у нас нет квадратных тригонометрических функций, все функции идут в первой степени. Как решаются такие конструкции? В первую очередь, давайте предположим, что cosx=0 cos x=0.

Подставим это значение в основное тригонометрическое тождество:

sin 2 x+ cos 2 x=1

Если эти числа, 0 и ±1, мы подставим в исходную конструкцию, то получим следующее:

Мы получили полный бред. Следовательно, наше предположение, что cosx=0 cos x=0 неверно, cosx cos x не может быть равен 0 в данном выражении. А если cosx cos x не равен 0, то давайте разделим обе стороны на cosx cos x:

И вот мы получили долгожданное простейшее выражение вида tg x=a tgx=a. Прекрасно, решаем его. Это табличное значение:

Мы нашли корень, мы решили первую часть задачи, т. е. честно заработали один первичный балл из двух.

Переходим ко второй части: найдите корни этого уравнения, принадлежащие промежутку, а, точнее, отрезку

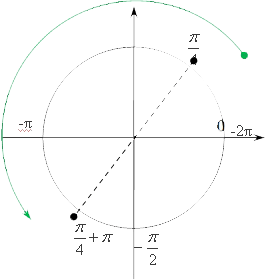
[left[ -2text!!pi!!text;-frac<text!!pi!!text> right]]. Предлагаю, как и в прошлый раз решать это выражение графически, т. е. нарисовать окружность, отметить в ней начало, т. е. 0, а также концы отрезка:

-2text!!pi!!text;-frac нужно найти все значения, которые принадлежат

frac<text!!pi!!text><text>+text!!pi!!textn. А теперь самое веселое: дело в том, что сама точка π 4 frac<text!!pi!!text> не принадлежит отрезку

π 4 ∉ ˜ [ −2 π ;− π 2 ]

Уже хотя бы потому, что оба конца этого отрезка отрицательные, а число π 4 frac<text!!pi!!text> положительное, но с другой стороны, какие-то значения вида

frac<text!!pi!!text>+text!!pi!!textn все-таки принадлежат нашему отрезку. Так как же их выделить? Очень просто: берем конец отрезка

-2text!!pi!!text и прибавляем π 4 frac<text!!pi!!text><text> , т. е. все происходит то же самое, как если бы мы начали отчет не от 0, а от −2 π -2text!!pi!!text, и у нас найдется первая точка:

x=−2 π + π 4 =− 7 π 4

Теперь второе число:

x=−2 π + π 4 + π =− 3 π 4

Это и есть второе значение. Других корней нет, потому что мы сами при их разметке и при отметке нашего отрезка ограничения обнаружили, что внутри этого отрезка лежат лишь два вида — π 4 frac<text!!pi!!text><text> и π 4 + π frac<text!!pi!!text>+text!!pi!!text. Эти точки мы и наши. Выписываем ответ:

За такое решение вы получите два первичных балла из двух возможных.

Видео:Косинус и синус двойного угла, часть 1. Алгебра 10 классСкачать

Что нужно помнить для правильного решения

Еще раз ключевые шаги, которые необходимо выполнить. В первую очередь, нужно знать выкладки двойного угла синуса или косинуса, в частности, именно в нашей задаче, косинус двойного угла. Кроме того, после его применения необходимо решить простейшее тригонометрическое уравнение. Решается оно довольно просто, однако необходимо написать и проверить, что cosx cos x в нашей конструкции не равен 0. После тригонометрического уравнения мы получаем элементарное выражение, в нашем случае это tg x=1 tgx=1, которое легко решается по стандартным формулам, известным еще с 9-10 класса. Таким образом, мы решим пример и получим ответ на первую часть задания — множество всех корней. В нашем случае это

frac<text!!pi!!text><text>+text!!pi!!textn,nin ˜Z. Затем остается лишь отобрать корни, принадлежащие отрезку

left[ -2text!!pi!!text;-frac<text!!pi!!text> right]. Для этого мы снова чертим тригонометрический круг, отмечаем на нем наши корни и наш отрезок, а затем отсчитываем от конца то самое π 4 frac<text!!pi!!text> и π 4 + π frac<text!!pi!!text>+text!!pi!!text, которые получились во время отметки всех корней вида π 4 + π n frac<text!!pi!!text><text>+text!!pi!!textn. После несложного счета мы получили два конкретных корня, а, именно,

-frac<3text!!pi!!text>, которые являются ответом ко второй части задачи, т. е. корнями, принадлежащими отрезку

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Ключевые моменты

Чтобы без проблем справиться с задачами C1 такого типа, запомните две основные формулы:

Синус двойного угла:

sin2 α =2sin α cos α

sin 2text!!alpha!!text=2sin text!!alpha!!textcos text!!alpha!!text — эта формула для синусов всегда работает именно в таком виде;

С первой все понятно. Но что за варианты возможны во втором случае? Дело в том, что косинус двойного угла можно записать по-разному:

cos2 α =cos2 α −sin2 α =2cos2 α −1=1−2sin2 α

cos 2text!!alpha!!text=cos 2text!!alpha!!text-sin 2text!!alpha!!text=2cos 2text!!alpha!!text-1=1-2sin 2text!!alpha!!text

Эти равенства следуют из основного тригонометрического тождества. Ну и какое равенство выбрать при решении конкретного примера C1? Все просто: если вы планируете свести конструкцию к синусам, то выбирайте последнее разложение, в котором присутствует только

sin 2text!!alpha!!text. И наоборот, если хотите свести все выражение к работе с косинусами, выбирайте второй вариант — тот, где косинус является единственной тригонометрической функцией.

Видео:10 класс, 27 урок, Формулы двойного аргумента. Формулы понижения степениСкачать

Основные виды тригонометрических уравнений (задание 13)

Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.

(blacktriangleright) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: [<Large>] где (ane 0, f(x)) — одна из функций (sin x, cos x, mathrm,x, mathrm, x) ,
то такое уравнение с помощью замены (f(x)=t) сводится к квадратному уравнению.

Часто при решении таких уравнений используются
основные тождества: [begin hline sin^2 alpha+cos^2 alpha =1&& mathrm, alpha cdot mathrm, alpha =1\ &&\ mathrm, alpha=dfrac&&mathrm, alpha =dfrac\&&\ 1+mathrm^2, alpha =dfrac1 && 1+mathrm^2, alpha=dfrac1\&&\ hline end]
формулы двойного угла: [begin hline sin =2sin alphacos alpha & qquad &qquad & cos=cos^2alpha -sin^2alpha\ sin alphacos alpha =dfrac12sin && & cos=2cos^2alpha -1\ & & & cos=1-2sin^2 alpha\ hline &&&\ mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac<mathrm^2, alpha-1><2mathrm, alpha>\&&&\ hline end]

Пример 1. Решить уравнение (6cos^2x-13sin x-13=0)

С помощью формулы (cos^2alpha=1-sin^2alpha) уравнение сводится к виду:
(6sin^2x+13sin x+7=0) . Сделаем замену (t=sin x) . Т.к. область значений синуса (sin xin [-1;1]) , то (tin[-1;1]) . Получим уравнение:

(6t^2+13t+7=0) . Корни данного уравнения (t_1=-dfrac76, t_2=-1) .

Таким образом, корень (t_1) не подходит. Сделаем обратную замену:
(sin x=-1 Rightarrow x=-dfrac2+2pi n, ninmathbb) .

Пример 2. Решить уравнение (5sin 2x=cos 4x-3)

С помощью формулы двойного угла для косинуса (cos 2alpha=1-2sin^2alpha) имеем:
(cos4x=1-2sin^22x) . Сделаем эту подстановку и получим:

(2sin^22x+5sin 2x+2=0) . Сделаем замену (t=sin 2x) . Т.к. область значений синуса (sin 2xin [-1;1]) , то (tin[-1;1]) . Получим уравнение:

(2t^2+5t+2=0) . Корни данного уравнения (t_1=-2, t_2=-dfrac12) .

Таким образом, корень (t_1) не подходит. Сделаем обратную замену: (sin 2x=-dfrac12 Rightarrow x_1=-dfrac+pi n, x_2=-dfrac+pi n, ninmathbb) .

Пример 3. Решить уравнение (mathrm, x+3mathrm,x+4=0)

Т.к. (mathrm,xcdot mathrm,x=1) , то (mathrm,x=dfrac1<mathrm,x>) . Сделаем замену (mathrm,x=t) . Т.к. область значений тангенса (mathrm,xinmathbb) , то (tinmathbb) . Получим уравнение:

(t+dfrac3t+4=0 Rightarrow dfrac=0) . Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:

Сделаем обратную замену:

(blacktriangleright) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: [<Large>] где (ane 0, f(x)) — одна из функций (sin x, cos x, mathrm,x, mathrm, x) ,
то такое уравнение с помощью замены (f(x)=t) сводится к кубическому уравнению.

Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: [begin hline &&&\ sin =3sin alpha -4sin^3alpha &&& cos=4cos^3alpha -3cos alpha\&&&\ hline end]

Пример 4. Решить уравнение (11cos 2x-3=3sin 3x-11sin x)

При помощи формул (sin 3x=3sin x-4sin^3x) и (cos2x=1-2sin^2x) можно свести уравнение к уравнению только с (sin x) :

(12sin^3x-9sin x+11sin x-3+11-22sin^2 x=0) . Сделаем замену (sin x=t, tin[-1;1]) :

(6t^3-11t^2+t+4=0) . Подбором находим, что один из корней равен (t_1=1) . Выполнив деление в столбик многочлена (6t^3-11t^2+t+4) на (t-1) , получим:

((t-1)(2t+1)(3t-4)=0 Rightarrow) корнями являются (t_1=1, t_2=-dfrac12, t_3=dfrac43) .

Таким образом, корень (t_3) не подходит. Сделаем обратную замену:

(blacktriangleright) Однородные тригонометрические уравнения второй степени: [I. quad <Large>, quad ane 0,cne 0]

Заметим, что в данном уравнении никогда не являются решениями те значения (x) , при которых (cos x=0) или (sin x=0) . Действительно, если (cos x=0) , то, подставив вместо косинуса ноль в уравнение, получим: (asin^2 x=0) , откуда следует, что и (sin x=0) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если (cos x=0) , то (sin x=pm 1) .

Аналогично и (sin x=0) не является решением такого уравнения.

Значит, данное уравнение можно делить на (cos^2 x) или на (sin^2 x) . Разделим, например, на (cos^2 x) :

Таким образом, данное уравнение при помощи деления на (cos^2x) и замены (t=mathrm,x) сводится к квадратному уравнению:

(at^2+bt+c=0) , способ решения которого вам известен.

Уравнения вида [I’. quad <Large>, quad ane0,cne 0] с легкостью сводятся к уравнению вида (I) с помощью использования основного тригонометрического тождества: [d=dcdot 1=dcdot (sin^2x+cos^2x)]

Заметим, что благодаря формуле (sin2x=2sin xcos x) однородное уравнение можно записать в виде

(asin^2 x+bsin 2x+ccos^2x=0)

Пример 5. Решить уравнение (2sin^2x+3sin xcos x=3cos^2x+1)

Подставим вместо (1=sin^2x+cos^2x) и получим:

(sin^2x+3sin xcos x-4cos^2x=0) . Разделим данное уравнение на (cos^2x) :

(mathrm^2,x+3mathrm,x-4=0) и сделаем замену (t=mathrm,x, tinmathbb) . Уравнение примет вид:

(t^2+3t-4=0) . Корнями являются (t_1=-4, t_2=1) . Сделаем обратную замену:

(blacktriangleright) Однородные тригонометрические уравнения первой степени: [II.quad <Large>, ane0, bne 0]

Заметим, что в данном уравнении никогда не являются решениями те значения (x) , при которых (cos x=0) или (sin x=0) . Действительно, если (cos x=0) , то, подставив вместо косинуса ноль в уравнение, получим: (asin x=0) , откуда следует, что и (sin x=0) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если (cos x=0) , то (sin x=pm 1) .

Аналогично и (sin x=0) не является решением такого уравнения.

Значит, данное уравнение можно делить на (cos x) или на (sin x) . Разделим, например, на (cos x) :

(a dfrac+b dfrac=0) , откуда имеем (amathrm, x+b=0 Rightarrow mathrm, x=-dfrac ba)

Пример 6. Решить уравнение (sin x+cos x=0)

Разделим правую и левую части уравнения на (sin x) :

(1+mathrm, x=0 Rightarrow mathrm, x=-1 Rightarrow x=-dfrac4+pi n, ninmathbb)

(blacktriangleright) Неоднородные тригонометрические уравнения первой степени: [II.quad <Large>, ane0, bne 0, cne 0]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: (<large<sin x=2sincos, qquad cos x=cos^2 -sin^2 ,qquad c=ccdot Big(sin^2 +cos^2 Big)>>) данное уравнение сведется к уравнению (I) :

Пример 7. Решить уравнение (sin 2x-sqrt3 cos 2x=-1)

Распишем (sin 2x=2sin xcos x, cos 2x=cos^2x-sin^2 x, -1=-sin^2 x-cos^2x) . Тогда уравнение примет вид:

((1+sqrt3)sin^2x+2sin xcos x+(1-sqrt3)cos^2x=0) . Данное уравнение с помощью деления на (cos^2x) и замены (mathrm,x=t) сводится к:

((1+sqrt3)t^2+2t+1-sqrt3=0) . Корнями этого уравнения являются (t_1=-1, t_2=dfrac=2-sqrt3) . Сделаем обратную замену:

2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: [begin hline &&&\ sin=dfrac<2mathrm, dfrac2><1+mathrm^2, dfrac2> &&& cos=dfrac<1-mathrm^2, dfrac2><1+mathrm^2, dfrac2>\&&&\ hline end] уравнение сведется к квадратному уравнению относительно (mathrm, dfrac x2)

Пример 8. Решить то же уравнение (sin 2x-sqrt3 cos 2x=-1)

(dfrac=0 Rightarrow (sqrt3+1)t^2+2t+1-sqrt3=0) (т.к. (1+t^2geqslant 1) при всех (t) , то есть всегда (ne 0) )

Таким образом, мы получили то же уравнение, что и, решая первым способом.

3 СПОСОБ: при помощи формулы вспомогательного угла.
[<large<asin x+bcos x=sqrt,sin (x+phi),>> quad text cos phi=dfrac a<sqrt>]

Для использования данной формулы нам понадобятся формулы сложения углов: [begin hline &&&\ sin=sinalphacdot cosbetapm sinbetacdot cosalpha &&& cos=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &&&\ hline end]

Пример 9. Решить то же уравнение (sin 2x-sqrt3 cos 2x=-1)

Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на (sqrt=2) :

(dfrac12sin 2x-dfrac2cos 2x=-dfrac12)

Заметим, что числа (dfrac12) и (dfrac2) получились табличные. Можно, например, взять за (dfrac12=cos dfrac3, dfrac2=sin dfrac3) . Тогда уравнение примет вид:

(sin 2xcos dfrac3-sin dfrac3cos 2x=-dfrac12 Rightarrow sinleft(2x-dfrac3right)=-dfrac12)

Решениями данного уравнения являются:

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.

(blacktriangleright) Если тригонометрическое уравнение можно свести к виду [<Large>, text ane 0, bne 0,] то с помощью формулы [<large> (*)] данное уравнение можно свести к квадратному.

Для этого необходимо сделать замену (t=sin xpm cos x) , тогда (sin xcos x=pm dfrac2) .

Заметим, что формула ((*)) есть не что иное, как формула сокращенного умножения ((Apm B)^2=A^2pm 2AB+B^2) при подстановке в нее (A=sin x, B=cos x) .

Пример 10. Решить уравнение (3sin 2x+3cos 2x=16sin xcos^3x-8sin xcos x) .

Вынесем общий множитель за скобки в правой части: (3sin 2x+3cos 2x=8sin xcos x(2cos^2 x-1)) .
По формулам двойного угла (2sin xcos x=sin 2x, 2cos^2x-1=cos 2x) имеем: [3(sin 2x+cos 2x)=4sin 2xcos 2x] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену (t=sin 2x+cos 2x) , тогда (sin 2xcos 2x=dfrac2) . Тогда уравнение примет вид: [3t=2t^2-2 Rightarrow 2t^2-3t-2=0] Корнями данного уравнения являются (t_1=2, t_2=-dfrac12) .

По формулам вспомогательного аргумента (sin2x+cos 2x=sqrt2sinleft(2x+dfrac4right)) , следовательно, сделав обратную замену: [left[ begin begin &sqrt2sinleft(2x+dfrac4right)=2\[1ex] &sqrt2sinleft(2x+dfrac4right)=-dfrac12 end end right. Rightarrow left[ begin begin &sinleft(2x+dfrac4right)=sqrt2\[1ex] &sinleft(2x+dfrac4right)=-dfrac1 end end right.] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от (-1) до (1) . Значит: (sinleft(2x+dfrac4right)=-dfrac1 Rightarrow left[ begin begin &2x+dfrac4=-arcsin <dfrac1>+2pi n\[1ex] &2x+dfrac4=pi+arcsin <dfrac1>+2pi n end end right. Rightarrow )
(Rightarrow left[ begin begin &x=-dfrac12arcsin <dfrac1>-dfrac8+pi n\[1ex] &x=dfrac8+dfrac12arcsin <dfrac1>+pi n end end right. ninmathbb)

(blacktriangleright) Формулы сокращенного умножения в тригонометрическом варианте:

(I) Квадрат суммы или разности ((Apm B)^2=A^2pm 2AB+B^2) :

((sin xpm cos x)^2=sin^2 xpm 2sin xcos x+cos^2x=(sin^2 x+cos^2 x)pm 2sin xcos x=1pm sin 2x)

(II) Разность квадратов (A^2-B^2=(A-B)(A+B)) :

((cos x-sin x)(cos x+sin x)=cos^2x-sin^2x=cos 2x)

(III) Сумма или разность кубов (A^3pm B^3=(Apm B)(A^2mp AB+B^2)) :

(sin^3xpm cos^3x=(sin xpm cos x)(sin^2xmp sin xcos x+cos^2x)=(sin xpm cos x)(1mp sin xcos x)=)

(=(sin xpm cos x)(1mp frac12sin 2x))

(IV) Куб суммы или разности ((Apm B)^3=A^3pm B^3pm 3AB(Apm B)) :

((sin xpm cos x)^3=(sin xpm cos x)(sin xpm cos x)^2=(sin xpm cos x)(1pm sin 2x)) (по первой формуле)

💥 Видео

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Решение тригонометрических уравнений. 10 класс.Скачать

Формулы двойного угла. 9 класс.Скачать

12 часов Тригонометрии с 0.Скачать

Решение тригонометрических уравнений. Метод понижения порядка. 10 класс.Скачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

СИНУС КОСИНУС ТАНГЕНС ДВОЙНОГО УГЛА тригонометрияСкачать

Тригонометрическое уравнение синуса двойного угла. Алгебра 10 классСкачать

Подготовка к ЕГЭ #92. Решение тригонометрических уравнений с помощью формул двойного углаСкачать

Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Все способы решения тригонометрических уравнений 12 задание проф. ЕГЭ по математикеСкачать

18+ Математика без Ху!ни. Формулы ПриведенияСкачать