Решение тригонометрических уравнений по формулам сложения (4 видео)

Формулы сложения: доказательство, примеры

Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.

Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.

Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.

Содержание

Основные формулы сложения в тригонометрии
Доказательства формул сложения
Способы решения тригонометрических уравнений
Тригонометрические уравнения — формулы, решения, примеры
Простейшие тригонометрические уравнения
Формулы корней тригонометрических уравнений в таблице
Методы решения тригонометрических уравнений
Алгебраический метод.
Разложение на множители.
Приведение к однородному уравнению
Переход к половинному углу
Введение вспомогательного угла
Дробно-рациональные тригонометрические уравнения
📽️ Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Основные формулы сложения в тригонометрии

Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.

1.Синус суммы двух углов можно получить следующим образом:

— вычисляем произведение синуса первого угла на косинус второго;

— умножаем косинус первого угла на синус первого;

— складываем получившиеся значения.

Графическое написание формулы выглядит так: sin ( α + β ) = sin α · cos β + cos α · sin β

2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin ( α — β ) = sin α · cos β + sin α · sin β

3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos ( α + β ) = cos α · cos β — sin α · sin β

4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos ( α — β ) = cos α · cos β + sin α · sin β

5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: t g ( α + β ) = t g α + t g β 1 — t g α · t g β

6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: t g ( α — β ) = t g α — t g β 1 + t g α · t g β

7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: c t g ( α + β ) = — 1 + c t g α · c t g β c t g α + c t g β

8. Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс c t g ( α — β ) = — 1 — c t g α · c t g β c t g α — c t g β .

Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков ± (плюс-минус) и ∓ (минус-плюс) мы можем сгруппировать их для удобства записи:

sin ( α ± β ) = sin α · cos β ± cos α · sin β cos ( α ± β ) = cos α · cos β ∓ sin α · sin β t g ( α ± β ) = t g α ± t g β 1 ∓ t g α · t g β c t g ( α ± β ) = — 1 ± c t g α · c t g β c t g α ± c t g β

Соответственно, мы имеем одну формулу записи для суммы и разности каждого значения, просто в одном случае мы обращаем внимание на верхний знак, в другом – на нижний.

Мы можем взять любые углы α и β , и формулы сложения для косинуса и синуса подойдут для них. Если мы можем правильно определить значения тангенсов и котангенсов этих углов, то формулы сложения для тангенса и котангенса будут также для них справедливы.

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Доказательства формул сложения

Как и большинство понятий в алгебре, формулы сложения могут быть доказаны. Первая формула, которую мы докажем, — формула косинуса разности. Из нее потом можно легко вывести остальные доказательства.

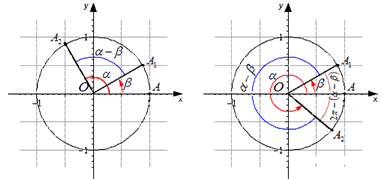
Уточним основные понятия. Нам понадобится единичная окружность. Она получится, если мы возьмем некую точку A и повернем вокруг центра (точки O ) углы α и β . Тогда угол между векторами O A 1 → и O A → 2 будет равняться ( α — β ) + 2 π · z или 2 π — ( α — β ) + 2 π · z ( z – любое целое число). Получившиеся вектора образуют угол, который равен α — β или 2 π — ( α — β ) , или он может отличаться от этих значений на целое число полных оборотов. Взгляните на рисунок:

Мы воспользовались формулами приведения и получили следующие результаты:

cos ( ( α — β ) + 2 π · z ) = cos ( α — β ) cos ( 2 π — ( α — β ) + 2 π · z ) = cos ( α — β )

Итог: косинус угла между векторами O A 1 → и O A 2 → равняется косинусу угла α — β , следовательно, cos ( O A 1 → O A 2 → ) = cos ( α — β ) .

Далее мы переходим к самому доказательству формулы косинуса разности.

Вспомним определения синуса и косинуса: синус — функция угла, равная отношению катета противолежащего угла к гипотенузе, косинус – это синус дополнительного угла. Следовательно, точки A 1 и A 2 имеют координаты ( cos α , sin α ) и ( cos β , sin β ) .

O A 1 → = ( cos α , sin α ) и O A 2 → = ( cos β , sin β )

Если непонятно, взгляните на координаты точек, расположенных в начале и конце векторов.

Длины векторов равны 1 , т.к. у нас единичная окружность.

Разберем теперь скалярное произведение векторов O A 1 → и O A 2 → . В координатах оно выглядит так:

( O A 1 → , O A 2 ) → = cos α · cos β + sin α · sin β

Из этого мы можем вывести равенство:

cos ( α — β ) = cos α · cos β + sin α · sin β

Таким образом, формула косинуса разности доказана.

Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление α + β = α — ( — β ) . У нас есть:

cos ( α + β ) = cos ( α — ( — β ) ) = = cos α · cos ( — β ) + sin α · sin ( — β ) = = cos α · cos β + sin α · sin β

Это и есть доказательство формулы косинуса суммы. В последней строчке использовано свойство синуса и косинуса противоположных углов.

Формулу синуса суммы можно вывести из формулы косинуса разности. Возьмем для этого формулу приведения:

вида sin ( α + β ) = cos ( π 2 ( α + β ) ) . Так
sin ( α + β ) = cos ( π 2 ( α + β ) ) = cos ( ( π 2 — α ) — β ) = = cos ( π 2 — α ) · cos β + sin ( π 2 — α ) · sin β = = sin α · cos β + cos α · sin β

А вот доказательство формулы синуса разности:

sin ( α — β ) = sin ( α + ( — β ) ) = sin α · cos ( — β ) + cos α · sin ( — β ) = = sin α · cos β — cos α · sin β
Обратите внимание на использование свойств синуса и косинуса противоположных углов в последнем вычислении.

Далее нам нужны доказательства формул сложения для тангенса и котангенса. Вспомним основные определения (тангенс – отношение синуса к косинусу, а котангенс –наоборот) и возьмем уже выведенные заранее формулы. У нас получилось:

t g ( α + β ) = sin ( α + β ) cos ( α + β ) = sin α · cos β + cos α · sin β cos α · cos β — sin α · sin β

У нас получилась сложная дробь. Далее нам нужно разделить ее числитель и знаменатель на cos α · cos β , учитывая что cos α ≠ 0 и cos β ≠ 0 , получаем:
sin α · cos β + cos α · sin β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β = sin α · cos β cos α · cos β + cos α · sin β cos α · cos β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β

Теперь сокращаем дроби и получаем формулу следующего вида: sin α cos α + sin β cos β 1 — sin α cos α · s i n β cos β = t g α + t g β 1 — t g α · t g β .
У нас получилось t g ( α + β ) = t g α + t g β 1 — t g α · t g β . Это и есть доказательство формулы сложения тангенса.

Следующая формула, которую мы будем доказывать – формула тангенса разности. Все наглядно показано в вычислениях:

t g ( α — β ) = t g ( α + ( — β ) ) = t g α + t g ( — β ) 1 — t g α · t g ( — β ) = t g α — t g β 1 + t g α · t g β

Формулы для котангенса доказываются схожим образом:
c t g ( α + β ) = cos ( α + β ) sin ( α + β ) = cos α · cos β — sin α · sin β sin α · cos β + cos α · sin β = = cos α · cos β — sin α · sin β sin α · sin β sin α · cos β + cos α · sin β sin α · sin β = cos α · cos β sin α · sin β — 1 sin α · cos β sin α · sin β + cos α · sin β sin α · sin β = = — 1 + c t g α · c t g β c t g α + c t g β
Далее:
c t g ( α — β ) = c t g ( α + ( — β ) ) = — 1 + c t g α · c t g ( — β ) c t g α + c t g ( — β ) = — 1 — c t g α · c t g β c t g α — c t g β

Примеры сложения с помощью тригонометрических формул

В этом пункте мы рассмотрим, как применить эти сложные на вид вычисления на практике. Их можно использовать:

— при преобразовании тригонометрических выражений;

— для вычисления точных значений синуса, косинуса, тангенса и котангенса углов, которые отличаются от основных ( 0 , π 6 , π 4 , π 3 , π 2 );

— для доказательства других тригонометрических формул, например, формулы двойного угла.

Разберем задачи с использованием формул сложения.

Задача: Вычислите точное значение тангенса 15 градусов.

Решение

Для наглядности мы 15 градусов можно представить в виде разности 45 — 30 . В этом случае решение задачи можно получить с помощью формулы тангенса разности. Возьмем формулу, которую мы приводили выше, и укажем в ней имеющиеся нам известные значения: t g 15 ° = t g ( 45 ° — 30 ° ) = t g 45 ° — t g 30 ° 1 + t g 45 ° · t g 30 °

Вычисляем ответ: t g 45 ° — t g 30 ° 1 + t g 45 ° · t g 30 ° = 1 — 3 3 1 + 1 · 3 3 = = 3 — 1 3 + 1 = ( 3 — 1 ) · ( 3 — 1 ) ( 3 + 1 ) · ( 3 — 1 ) = ( 3 ) 2 — 2 3 + 1 ( 3 ) 2 — 1 = 2 — 3

Ответ: t g 15 ° = 2 — 3

Задача: Выберем формулу сложения для проверки формулы приведения следующего вида: sin ( π 2 + α ) = cos α

Нам подойдет формула синуса суммы. Итого: sin ( π 2 + α ) = sin π 2 · cos α + cos π 2 · sin α = 1 · cos α + 0 · sin α = cos α

Ответ: sin ( π 2 + α ) = cos α — наша формула доказана.

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Способы решения тригонометрических уравнений

Министерство образования и молодёжной политики Чувашской Республики

Муниципальное образовательное учреждение

«Средняя общеобразовательная школа №6 г. Чебоксары»

Способы решения тригонометрических уравнений

МОУ «Средняя общеобразовательная школа №6

Методическая разработка по теме «Способы решения тригонометрических уравнений». В средней школе на изучение данной темы отводится незначительное количество часов. Эта разработка изучит, расширит и углубит математические знания по данной теме.

На экзаменах по математике для поступающих в ВУЗы, олимпиадах часто встречаются задания на решение тригонометрических уравнений.

Все приводимые способы направлены на развитие познавательного интереса к предмету, знакомящие учащихся с новыми идеями и методами, расширяющие представления об изучаемой теме в основной школе.

Уравнения, предлагаемые в данной разработке, интересны, красивы, носят прикладной характер, что позволяет повысить учебную мотивацию учащихся и интерес к предмету и вызвать желание узнать больше.

Основные цели методической разработки:

· знакомство учащихся с основными приемами и методами решения тригонометрических уравнений;

· развитие навыков применения теоретических сведений по данной теме на практике в различных проявлениях;

· развитие творческих способностей;

· повышение интереса к предмету;

· повторение и обобщение знаний по теме «Способы решения тригонометрических уравнений;

· оказание помощи учащимся систематизировании уравнений и нахождении рациональных приемов решения.

Особенность методической разработки.

Использование материала в работе даст положительные результаты при подготовке школьников к сдаче ЕГЭ по математике.

1. Уравнения, приводимые к алгебраическим. . . . . . . . . . . . .. . . . . . . . . . . . . . . .4

2. Уравнения, решаемые разложением на множители. . . . . . . . . . . . . . . . . . . . . .5

3. Однородные уравнения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

4. Уравнения, решаемые с помощью формул сложения тригонометрических функций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

5. Уравнения, решаемые с помощью формул сложения углов и разложения произведения тригонометрических функций в сумму. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7

6. Уравнения, решаемые с помощью формул понижения степени. . . . . . . . . . . .8

7. Уравнения вида .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9

8. Уравнения смешанного типа. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

9. Задания для промежуточного и итогового контроля результатов обучения. .13

10. Тригонометрическое уравнение на ЕГЭ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

11. Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

1. Уравнение .

Если для любого t. Если , то формула корней уравнения такова:

2. Уравнение .

При уравнение не имеет решений, так как для любого . Если |a|≤1,то формула для записи всех решений уравнения такова: Удобно записывать не двумя, а одной формулой:

3. Уравнение . Решение данного уравнения имеет вид:.

4. Уравнение . Решение данного уравнения имеет вид:

Способы решения тригонометрических уравнений.

I. Уравнения, приводимые к алгебраическим

Пример. Решить уравнение

Решение. Воспользуемся тем, что . Тогда заданное уравнение можно переписать в виде . После понятных преобразований получим . Введем новую переменную . Тогда уравнение примет вид , откуда находим . Значит,. Из этих уравнений находим, соответственно,

Уравнения для самостоятельного решения:

II. Уравнения, решаемые разложением на множители

Смысл этого метода: если уравнение удается преобразовать к виду , то задача сводится к решению двух уравнений, то есть к решению совокупности уравнений: .

Пример. Решить уравнение .

Решение. Имеем . Значит, приходим к совокупности уравнений . Из первого уравнения находим . Из второго уравнения находим .

Уравнения для самостоятельного решения:

III. Однородные уравнения.

Определение. Уравнение вида, где называют однородным тригонометрическим уравнением первой степени, уравнение вида ¸называют однородным тригонометрическим уравнением второй степени.

Итак, дано уравнение . Разделив обе части уравнения почленно на , получим .

Но, внимание! Делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в рассматриваемом случае отличен от 0? Давайте проанализируем. Предположим, что cos x =0. Тогда однородное уравнение asinx+bcosx=0 примет вид asinx=0¸ то есть sinx=0¸ так как a≠0. Получается, что и cosx=0¸ и sinx=0¸ а это невозможно, так как sinx и cosx обращается в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения на cosx— вполне благополучная операция.

Пример 1. Решить уравнение 2sinx-3cosx= 0.

Решение. Разделим обе части уравнения почленно на cosx¸ получим . Рассмотрим теперь однородное тригонометрическое уравнение второй степени . Если коэффициент a отличен от нуля, то есть в уравнении содержится член sin2x с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной cos x не обращается в нуль, а потому можно обе части уравнения разделить почленно на .

Это — квадратное уравнение относительно новой переменной z= tgx .

Пример 2. Решить уравнение .

Решение. Разделим обе части уравнения почленно на cos2 x, получим Введя новую переменную получим, . Откуда находим z=1, z=2. Значит, либо tgx=1, либо tgx=2. Из первого уравнения находим Из второго уравнения находим .

Уравнения для самостоятельного решения:

IV. Уравнения, решаемые с помощью формул сложения тригонометрических функций.

позволяют сумму или разность синусов или косинусов разложить на множители.

Пример. Решить уравнения: sin5x + sinx=0;

Решение. Преобразовав сумму синусов в произведение, получим

Значит, либо , откуда находим , либо cos2x=0, откуда находим

Уравнения для самостоятельного решения:

V. Уравнения, решаемые с помощью формул сложения углов и разложения произведения тригонометрических функций в сумму

при решении тригонометрических уравнений.

Уравнения для самостоятельного решения:

VI. Уравнения, решаемые с помощью формул понижения степени

Пример. Решить уравнение

Уравнения для самостоятельного решения:

VII. Уравнения вида

Преобразование выражения Итак, Аналогично можно выражение преобразовать к виду .

Пример.

Здесь Имеем Введём вспомогательный аргумент , удовлетворяющий соотношениям например, . Тогда

Уравнения для самостоятельного решения:

VIII. Уравнения смешанного типа

1. Решите уравнения:

Выбор корней проведём на тригонометрической окружности

Ответ:

а)

Ответ:

в)

Ответ:

б)

Ответ:

г)

Ответ:

2. Решите уравнения.

Не удовлетворяет условию

Выберем те значения x, которые удовлетворяют условию

Ответ:

а)

Ответ:

в)

Ответ:

б)

Ответ:

г)

Ответ:

3. Решите уравнение.

Данное уравнение равносильно системе:

Решим второе уравнение системы:

не удовлетворяет условию

Выберем те значения х, которые удовлетворяют условию .

Ответ:

4. Решите уравнения.

Число корней на .

Выбор корней проведём на тригонометрической окружности.

Число решений на равно 5.

а)

Найти число решений на .

б) .

Найти число решений на

в)

Найти число решений на .

г) .

Найти число решений на .

5. Основной идеей решения следующих заданий является выражение синуса или косинуса через тангенс или котангенс половинного аргумента (или наоборот). При этом следует иметь в виду, что в формулах область определения «левых частей» равенств – все действительные числа, а область определения «правых частей» — .

Поэтому переход от одного уравнения к другому с использованием этих формул, вообще говоря, сужает ОДЗ на множество π.

Аналогичная ситуация с формулами

Вообще, использование формул, у которых ОДЗ «левых» и «правых» частей не совпадают, может привести либо к потере, либо к появлению посторонних корней.

Примерами таких формул являются:

Ответ:

а) . Ответ: .

в) .

Ответ: .

б) . Ответ: .

г) .

Ответ: .

IX. Задания для промежуточного контроля результатов обучения (ответы даны в скобках).

Уравнения, приводимые к алгебраическим.

Уравнения, решаемые способом разложения на множители.

Уравнения, решаемые с помощью формул сложения тригонометрических функций.

Уравнения, решаемые с помощью формул сложения углов и разложения произведения тригонометрических функций в сумму.

Уравнения, решаемые с помощью формул понижения степени.

Уравнения вида .

Уравнения смешанного типа.

2.Найти наименьший корень уравнения на интервале

Тест. Решение тригонометрических уравнений.

1. Найдите корни уравнения на интервале .

а) ; б) ; в) .

2. Найдите наибольший отрицательный корень уравнения

а) ; б) ; в) .

3. Решите уравнение: и найдите сумму корней, принадлежащих интервалу

а) ; б) ; в) .

4. Решите уравнение: и найдите сумму корней, принадлежащих интервалу .

а) ; б) ; в) .

Задания для итогового контроля результатов обучения.

1. Решите уравнения:

а) ; б) ;

в) ; г) ;

д) ; е) .

2. Найдите сумму корней управления

на промежутке .

3. Укажите количество корней уравнения

4. Решите уравнения:

а) ;

б) .

1. а) ; б) ; в) ; г) ;

д) ; е) . 2. 16. 3. 3. 4. а) ;

б) .

X. Тригонометрическое уравнение на ЕГЭ.

Решите уравнение . (С2,2007г.)

ОДЗ уравнения:

Используя способ разложения на множители, получим

или .

не удовлетворяет условию ОДЗ уравнения.

Используя способ решения однородного уравнения первой степени, получим:

С учетом ОДЗ уравнения решение данного уравнения имеет вид:

1. , , . Углубленное изучение курса алгебры и математического анализа для 10-11 класса, Москва, Просвещение, 1997 г.

2. , . Факультативный курс по математике: Решение задач: Учебное пособие для 11 кл. средней школы – М., Просвещение, 1999.

3. Журнал «Математика в школе», 2006, № 10.

4. , , . Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Математика. – М. Интеллект-Центр, 2002-2007 г.

5. . Математика. Гтовимся к ЕГ, 2005.

6. . Алгебра и начала анализа; Учебник для 10-11 кл. средней школы – 2-е изд. – М. Просвещение, 2000.

7. , , . Алгебра и начала анализа: Учебник для 10-11 кл. средней школы – 4-е изд. – М. Просвещение, 2002.

8. и др. Алгебра и начала анализа.10-11 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. Ч2: Задач. Для общеобразоват. учреждений.- 5-е изд.-М.:Мнемозина,2004.

Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Тригонометрические уравнения — формулы, решения, примеры

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.

Видео:12 часов Тригонометрии с 0.Скачать

Простейшие тригонометрические уравнения

Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.

1. Уравнение `sin x=a`.

При `|a|>1` не имеет решений.

При `|a| leq 1` имеет бесконечное число решений.

Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| leq 1` имеет бесконечное множество решений.

Формула корней: `x=pm arccos a + 2pi n, n in Z`

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + pi n, n in Z`

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + pi n, n in Z`

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Формулы корней тригонометрических уравнений в таблице

Для синуса:Для косинуса:Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:

Видео:Формулы приведения - как их легко выучить!Скачать

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

с помощью тригонометрических формул преобразовать его до простейшего;
решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.

Рассмотрим на примерах основные методы решения.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`

Решение. Используя формулы приведения, имеем:

`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,

делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,

находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:

1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.

2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.

Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.

Разложение на множители.

Пример. Решить уравнение: `sin x+cos x=1`.

Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

`sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
`cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.

Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.

Приведение к однородному уравнению

Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:

`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).

Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.

Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.

Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:

`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда: