Решение тригонометрических уравнений и неравенств конспект кратко (3 видео)

Урок по теме «Решение тригонометрических неравенств»

Разделы: Математика

Тема “Тригонометрические неравенства” является объективно сложной для восприятия и осмысления учащимися 10-го класса. Поэтому очень важно последовательно, от простого к сложному формировать понимание алгоритма и вырабатывать устойчивый навык решения тригонометрических неравенств.

Успех освоения данной темы зависит от знания основных определений и свойств тригонометрических и обратных тригонометрических функций, знания тригонометрических формул, умения решать целые и дробно-рациональные неравенства, основные виды тригонометрических уравнений.

Особый упор нужно делать на методике обучения решения простейших тригонометрических неравенств, т.к. любое тригонометрическое неравенство сводится к решению простейших неравенств.

Первичное представление о решении простейших тригонометрических неравенств предпочтительно вводить, используя графики синуса, косинуса, тангенса и котангенса. И только после учить решать тригонометрические неравенства на окружности.

Остановлюсь на основных этапах рассуждения при решении простейших тригонометрических неравенств.

Находим на окружности точки, синус (косинус) которых равен данному числу.
В случае строгого неравенства отмечаем на окружности эти точки, как выколотые, в случае нестрогого – как заштрихованные.
Точку, лежащую на главном промежутке монотонности функции синус (косинус), называем Р_t1, другую точку – Р_t2.
Отмечаем по оси синусов (косинусов) промежуток, удовлетворяющий данному неравенству.
Выделяем на окружности дугу, соответствующую данному промежутку.
Определяем направление движения по дуге (от точки Р_t1 к точке Р_t2по дуге), изображаем стрелку по направлению движения, над которой пишем знак “+” или “-” в зависимости от направления движения. (Этот этап важен для контроля найденных углов. Ученикам можно проиллюстрировать распространенную ошибку нахождения границ интервала на примере решения неравенства по графику синуса или косинуса и по окружности).
Находим координаты точек Р_t1 (как арксинус или арккосинус данного числа)и Р_t2т.е. границы интервала, контролируем правильность нахождения углов, сравнивая t₁и t_2.
Записываем ответ в виде двойного неравенства (или промежутка) от меньшего угла до большего.

Рассуждения при решении неравенств с тангенсом и котангенсом аналогичны.

Рисунок и запись решения, которые должны быть отражены в тетради у учеников, приведены в предлагаемом конспекте.

Конспект урока по теме: “Решение тригонометрических неравенств”.

Задача урока – продолжить изучение решения тригонометрических неравенств, содержащих функции синус и косинус, перейти от простейших неравенств к более сложным.

закрепление знаний тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;

формирование навыка решения простейших тригонометрических неравенств;

освоение приёмов решения более сложных тригонометрических неравенств;

развитие логического мышления, смысловой памяти, навыков самостоятельной работы, самопроверки;

воспитание аккуратности и чёткости в оформлении решения, интереса к предмету, уважения к одноклассникам.

формирование учебно-познавательных, информационных, коммуникативных компетенций.

Оборудование: графопроектор, раздаточные карточки с готовыми чертежами тригонометрических кругов, переносная доска, карточки с домашним заданием.

Форма организации обучения – урок. Методы обучения, используемые на уроке – словесные, наглядные, репродуктивные, проблемно-поисковые, индивидуального и фронтального опроса, устного и письменного самоконтроля, самостоятельной работы.

Этапы урока

Содержание

Организация класса на работу.

Проверка домашнего задания.

(Сбор тетрадей с домашней работой)

Формулировка цели урока.

– Сегодня на уроке повторим решение простейших тригонометрических неравенств и рассмотрим более сложные случаи.

Устная работа.

(Задания и ответы записаны на кодоскопной ленте, открываю ответы по ходу решения)

sinx = —, 2sinx =, sin2x = , sin(x – ) = 0, cosx = ,

cosx = —, cos2x = 1, tgx = -1.

Назовите главные промежутки монотонности функций синус и косинус.

Повторение.

– Вспомним алгоритм решения простейших тригонометрических неравенств.

(На доске – заготовки двух окружностей. Вызываю по одному двух учащихся для решения неравенств.Ученик подробно объясняет алгоритм решения.Класс работает совместно с отвечающими у доски на заранее подготовленных карточках с изображением окружности).

1) sinx —;

t₁ = arccos(-) = p – arccos =

= p – = ;

t_{2 = —};

— + 2p n t₂;

t₁ = arcsin = ;

t_{2 =} -p — = —;

+ 2p n 2 2x – 2cos2x 0.

(Вспомним прием решения тригонометрических уравнений вынесением общего множителя за скобку).

cos2x(cos2x – 2) 0.

Замена: cos2x = t, 1; t(t – 2) 0; Второе неравенство не удовлетворяет условию 1.

cos2x 0. (Решить неравенство самостоятельно. Проверить ответ).

Ответ: + p n 2 x – 5sinx + 1 0.

(Вспомним прием решения тригонометрических уравнений заменой переменной. У доски решает ученик с комментариями).

Замена sinx = t, 1. 6t 2 – 5t +1 0, 6(t – )(t – ),

Ответ: + 2p n х + 2p n, -p -arcsin+ 2p k х arcsin+ 2p k, n, k Z.

№3. sinx + cos2x> 1.

(Обсуждаем варианты решения. Вспоминаем фомулу косинуса двойного угла. Класс решает самостоятельно, один ученик – на индивидуальной доске с последующей проверкой).

sinx + cos2x – 1> 0, sinx – 2sin 2 x> 0, sinx(1 – 2sinx) > 0,

2p n 2 + () 2 = 1, то существует такой угол , что cos = , а sin = . Перепишем предыдущее неравенство в виде: sin(x + ) . Последнее неравенство, а, значит, и исходное неравенство имеет хотя бы одно решение при каждома таком, что -1, то есть при каждом а -5. Ответ: а -5.

Домашнее задание.

(Раздаю карточки с записью домашнего задания.Комментирую решение каждого неравенства).

cosx > sin 2 x;
4sin2xcos2x 2 sin 2 – 0,5;
sinx + cosx > 1.

Повторить тригонометрические формулы сложения, подготовиться к самостоятельной работе.

Подведение итогов, рефлексия.

– Назовите приемы решения тригонометрических неравенств.

– Каким образом знание алгоритма решения простейших тригонометрических неравенств используется при решении более сложных неравенств?

– Какие неравенства вызвали наибольшее затруднение?

(Оцениваю работу учащихся на уроке).

Самостоятельная работа
по результатам освоения материала

Вариант 1

Решите неравенства 1 – 3:

sin3x – 2 x + 3cosx > 0;
coscos2x – sinsin2x —.
Определите все а, при каждом из которых неравенство 12sinx + 5cosx а имеет хотя бы одно решение.

Вариант 2

Решите неравенства 1 – 3:

2cos> 1;
sin 2 x – 4sinx

Содержание

Решение тригонометрических уравнений и неравенств конспект кратко
Методы решения тригонометрических уравнений.
1. Алгебраический метод.
2. Разложение на множители.
3. Приведение к однородному уравнению.
4. Переход к половинному углу.
5. Введение вспомогательного угла.
6. Преобразование произведения в сумму.
Тригонометрические неравенства и методы их решения
🌟 Видео

Видео:Как решать тригонометрические неравенства?Скачать

Решение тригонометрических уравнений и неравенств конспект кратко

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Методы решения тригонометрических уравнений.

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

1. Алгебраический метод.

( метод замены переменной и подстановки ).

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Тригонометрические неравенства и методы их решения

Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.

Методы решений неравенств:

Решение тригонометрических неравенств с помощью единичной окружности.
Графическое решение тригонометрических неравенств.
Решение неравенств методом интервалов.

При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:

I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.

II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.

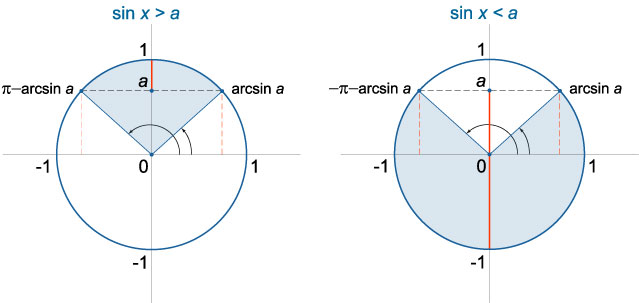
Неравенство (sinx>a)

При (|a|≥1) неравенство (sinx>a) не имеет решений: (xin varnothing) .
При (a решением неравенства (sinx>a) является любое действительное число: (xin mathbb R) .
При (−1≤a решение неравенства (sinx>a) выражается в виде (arcsin a + 2pi n .

Неравенство (sinx≥a)

Неравенство (sinx

Неравенство (sinx≤a)

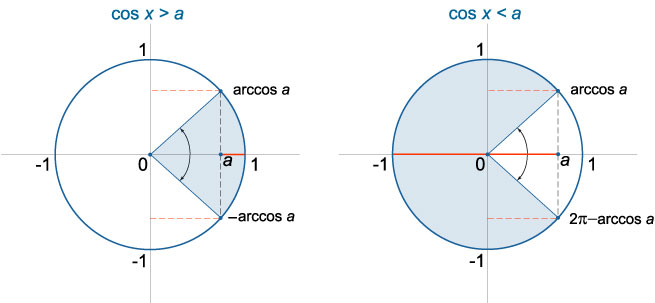
Неравенство (cosx>a)

При (a≥1) неравенство (cosx>a) не имеет решений: (xin varnothing) .
При (a решением неравенства (cosx>a) является любое действительное число: (xin mathbb R) .
При (−1≤a решение неравенства (cosx>a) имеет вид (-arccos a + 2pi n .

Неравенство (cosx≥a)

Неравенство (cosx

Неравенство (cosx≤a)

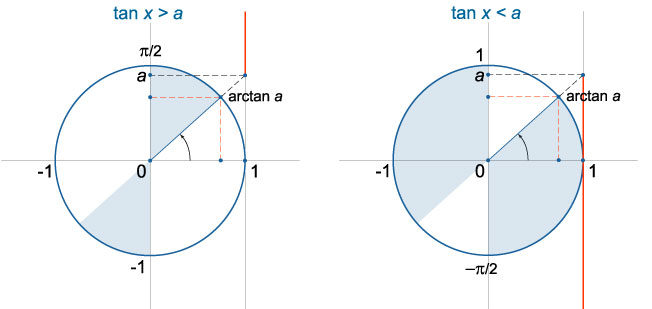
Неравенство (tgx>a)

При любом действительном значении (a) решение строгого неравенства (tgx>a) имеет вид (arctg a + pi n .

Неравенство (tgx≥a)

Для любого значения (a) решение неравенства (tgx≥a) выражается в виде (arctg a + pi n le x .

Неравенство (tgx

Для любого значения (a) решение неравенства (tgx записывается в виде (-frac2 + pi n .

Неравенство (tgx≤a)

При любом (a) неравенство (tgx≤a) имеет следующее решение: (-frac2 + pi n .

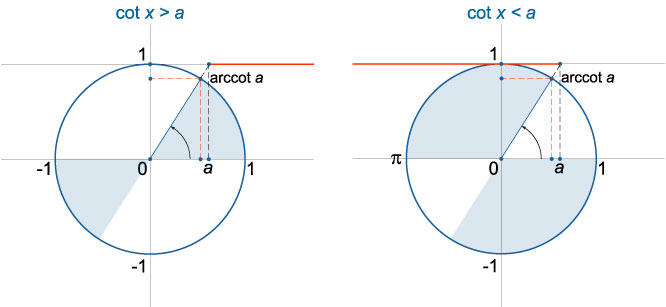
Неравенство (ctgx>a)

При любом (a) решение неравенства (ctgx>a) имеет вид (pi n .

Неравенство (ctgx≥a )

Нестрогое неравенство (ctgx≥a) имеет аналогичное решение (pi n .

Неравенство (ctgx

Для любого значения (a) решение неравенства (ctgx лежит в открытом интервале (arcctg a + pi n .

Неравенство (ctgx≤a)

При любом (a) решение нестрогого неравенства (ctgx≤a) находится в полуоткрытом интервале (arcctg a + pi n le x .

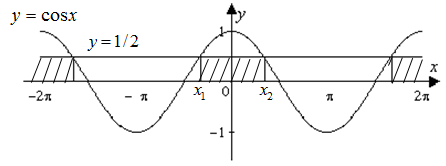
Пример. Решите неравенство: (cosx>frac12) .

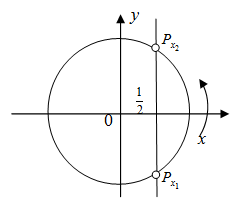
Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.

Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть (y=cosx и y=frac12) . Выделим промежутки, на которых график функции косинус (y=cosx) расположен выше графика прямой (y=frac12) .

Найдем абсциссы точек (x_1 и x_2) – точек пересечения графиков функций (y=cosx и y=frac12) , которые являются концами одного из промежутков, на котором выполняется указанное неравенство: (x_1=-arccosfrac12=-frac3; x_2=arccosfrac12=frac3) .

Учитывая, что косинус – функция периодическая, с периодом (2pi) , ответом будут значения x из промежутков ((-frac3+2pi k;frac3+2pi k), kin Z) .

Второй способ. Построим единичную окружность и прямую (x=frac12) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим (P_ и P_) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше (frac12) . Найдем значение (x_1 и x_2) , совершая обход против часовой стрелки так, чтобы (x_1 :

Учитывая периодичность косинуса, окончательно получим интервалы ((-frac3+2pi k;frac3+2pi k), kin Z) .