Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
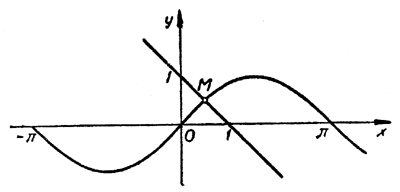
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
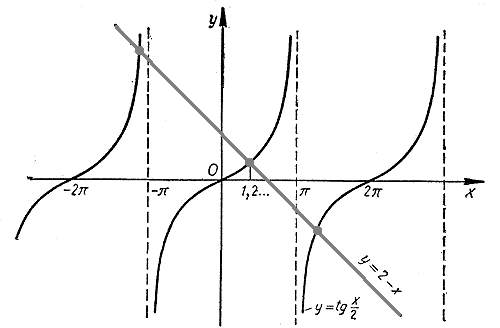
Графики функций у = tg x /2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
- Решение тригонометрических уравнений и неравенств функционально-графическим способом.
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом. 10-й класс
- Презентация к уроку
- 📹 Видео
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение тригонометрических уравнений и неравенств функционально-графическим способом.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Тема: Практическое занятие по теме «Решение тригонометрических уравнений и неравенств функционально-графическим способом».
Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
ПРИМЕР1: Пусть, например, нужно решить уравнение sin х = 1 — х .
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки, и дает нам единственный корень нашего уравнения.
ПРИМЕР 2: Решить уравнение и неравенство графическим способом на интервале (-
На одном и том же рисунке начертим два графика: график функции и график функции у = .
У нас получилось 4 точки пересечения на интервале (-. Абсциссы этих точек и являются решением уравнения. А интервалы, на которых график находится выше прямой у = , являются решением неравенства.
Задание: Выполнить уравнения и неравенства
Решите на интервале ( : А) уравнение 0
«4» — №1, №2 №3 одну из систем
Краткое описание документа:
В данной работе представлен краткий материал для самостоятельного изучения студентами темы «Решение тригонометрических уравнений и неравенств функционально-графическим способом».Длярешения уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. И тогда используем графический способ.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 956 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 685 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 314 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 570 248 материалов в базе
Материал подходит для УМК
«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
Глава 7. Тригонометрические функции
Другие материалы
- 18.06.2020
- 367
- 4
- 11.04.2020
- 122
- 8
- 19.01.2020
- 195
- 6
- 17.12.2019
- 437
- 8
- 25.11.2019
- 169
- 1
- 22.11.2019
- 169
- 1
- 22.11.2019
- 1106
- 4
- 22.11.2019
- 1369
- 3
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.06.2020 552
- DOCX 873.6 кбайт
- 16 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Илясова Светлана Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет
- Подписчики: 2
- Всего просмотров: 10393
- Всего материалов: 14
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:13 Функционально графический способ решенияСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля
Время чтения: 1 минута
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
В России действуют более 3,5 тысячи студенческих отрядов
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом. 10-й класс
Класс: 10
Презентация к уроку
Оборудование: ПК, проектор, экран, аудиторная доска.
Тип занятия: изучение нового материала.
| Образовательная цель: | сформировать навык решения тригонометрических неравенств, используя графический метод решения неравенств; отработать навыки построения графиков тригонометрических функций; познакомить учащихся с основоположниками тригонометрии и историей ее развития. |
| Развивающая цель: | обеспечить условия для развития умений анализировать, выделять главное, устанавливать единые общие признаки и свойства; научить применять знания на практике; научить критически оценивать свои знания. |
| Воспитательная цель: | воспитывать положительное отношение к знаниям; воспитывать дисциплинированность и добросовестность при выполнении заданий; воспитывать умение работать в парах (чувствовать индивидуальную ответственность за достижение результата). |
Задачи:
- повторить следующие темы по математике: решение квадратных неравенств графическим способом, преобразование графиков тригонометрических функций, понятие arcsin, arccos, arctg и arcctg числа, решение тригонометрических уравнений;
- научить применять графический метод для решения тригонометрических неравенств;
- отработать навыки построения графиков тригонометрических функций;
- расширить кругозор учащихся об истории развития Тригонометрии;
- для активизации познавательной деятельности учащихся применять различные формы и методы работы на уроке: фронтальная, индивидуальная и групповая (работа в парах) формы работы, использование игровых технологий.
Структура занятия:
- Организационный момент, проверка домашнего задания (3 мин.);
- Актуализация опорных знаний и фиксация затруднений в деятельности (5 мин.);
- Объяснение нового материала (10 мин.);
- Экспертная работа (5 мин.);
- Самостоятельная работа в парах (10 мин.);
- Домашнее задание (2 мин.);
- Игра “Поле чудес” (6 мин.);
- Рефлексия деятельности (итог урока) (4 мин.).
Пояснение к уроку: во время урока учащиеся выставляют баллы в “Рабочую карту урока” согласно правилам, описанным в данной карте. В конце урока подводится итог работы учащихся по количеству набранных баллов.
1. Организационный момент, проверка домашнего задания
Французский писатель Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом.”.
Давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.
Прежде чем приступить к изучению нового материала, проверим домашнее задание на сегодня.
Проверка домашнего задания:
№ 11.27 (а, б), № 11.29 (б, е), № 11.30 (б)
Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.
За каждое правильно выполненное задание – 1 балл в рабочую карту занятия в колонку “Домашняя работа”.
2. Актуализация опорных знаний и фиксация затруднений в деятельности
Тема нашего урока – Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом.
Давайте запишем дату и тему урока в тетрадь.
Перед Вами на сегодня стоит задача – научиться применять графический метод для решения тригонометрических неравенств.
Поработаем сначала устно, чтобы вспомнить те понятия и приемы, которые нам понадобятся для изучения новой темы.
За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.
Инструкция по работе с презентацией: при подведении курсора к ответу и нажатии левой кнопки мыши: неверные ответы исчезают, а в области верного ответа всплывает окно со словом “Верно”.
3. Объяснение нового материала
Если вспомнить определение тригонометрического уравнения – это уравнение, содержащее переменную под знаком тригонометрической функции, тогда легко можно дать определение тригонометрического неравенства – это неравенство, содержащие переменную под знаком тригонометрической функции.
Для решения тригонометрических неравенств мы будем использовать графический метод.
Рассмотрим решение неравенства
Построим график функции: 

Определим точки пересечения данных графиков:
Заштрихуем область, при которой значения функции 

Так как функция 


Ответ: 
Рассмотрим решение неравенства
Пусть 
Рассмотрим графики функций 



Получим неравенство
Следовательно,
Ответ: 

4. Экспертная работа
К доске приглашаются двое учащихся, хорошо разобравшихся в материале и желающих ответить у доски, они будут выступать в роли экспертов, остальные учащиеся могут поправлять их решение по мере надобности с места.
1. 

2. 

За работу у доски учащиеся получают 1-3 балла, за работу с места 1 балл.
5. Самостоятельная работа в парах
Прежде чем перейти к выполнению самостоятельной работы, необходимо заметить, что при решении более сложных тригонометрических неравенств, их с помощью преобразований сводят к простейшим тригонометрическим неравенствам, используя при этом те же приёмы, что и при решении тригонометрических уравнений.
Учащиеся выполняют задание, обмениваются тетрадями и проверяют работу соседа по парте, выставляя соответствующие баллы, ответы представлены на экране, подробное решение неравенств под номером 3 необходимо заранее подготовить на аудиторной доске.
Для решения тригонометрических неравенств графическим методом можно использовать Приложение № 2 к данному уроку.
| Вариант № 1 Решить неравенства | Вариант № 2 Решить неравенства |
1.  | 1.  |
2.  | 2.  |
 |   |
За каждое верное задание № 1,2-1 балл, № 3 – 3 балла.
Подведение итогов изучения новой темы. Учащимся необходимо ответить на вопросы учителя.
Вопросы:
- Какой метод мы использовали для решения тригонометрических неравенств?
- Что необходимо предпринять, чтобы решить тригонометрическое неравенство графическим способом?
- Как влияет периодичность тригонометрических функций на ответ при решении тригонометрических неравенств?
За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.
6. Домашнее задание
Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.
п. 11.5, 11.6, № 11.34 (б), 11.36 (в), 11.37 (в), 11.38 (б), 11.41 (б)
Дополнительное задание (по желанию):
Решить неравенство
7. Игра “Поле чудес”
Игра построена по принципу одноименной телевизионной игры. Учитель читает задание, учащиеся могут открыть любую букву, если выполнят скрытое в данной ячейке задание.
За каждую угаданную букву (решенное задание) учащиеся получают 1 балл, за отгаданное слово – 5 баллов.
Инструкция по работе с презентацией: при подведении курсора к ячейке, за которой скрывается буква, и нажатии левой кнопки мыши: появляется задание, которое необходимо выполнить, при повторном нажатии левой кнопки мыши в данную область появляется скрытая там буква.
Древнегреческий астроном, географ и математик II века до н.э., часто называемый величайшим астрономом античности. Главной заслугой его считается то, что он привнёс в греческие геометрические модели движения небесных тел предсказательную точность астрономии Древнего Вавилона.
При разработке теорий Луны и Солнца он использовал античный вариант тригонометрии. Возможно, он первым составил таблицу хорд, аналог современных таблиц тригонометрических функций.
Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др.
Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1731 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С.К. Котельников) и астрономы (С.Я. Румовский) были его учениками.
Аналитическая теория тригонометрических функций в основном была создана этим выдающимся математиком XVIII века. Именно он первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.
Ответ: Леонард Эйлер
Наука об измерении треугольников. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре..
Раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.
Рефлексия деятельности (итог урока)
Рабочая карта занятия
о/т — оценка товарища, о/у- оценка учителя, с/о – самооценка, о/г-оценка группы
с/о
Общее количество баллов, по 1 за каждое правильно выполненное задание.
о/у
Общее количество баллов, по 1 за каждый правильный ответ.
о/г
1-3 балла за работу у доски,
1 балл за работу с места.
о/т
За каждое верное задание
№ 3 – 3 балла.
о/у
Общее количество баллов, по 1 за каждый правильный ответ, за отгаданное слово – 5 баллов.
- 16 и более баллов – оценка “5”
- 11 — 15 баллов – оценка “4”
- 6 — 10 баллов – оценка “3”
Литература:
- Никольский, С.М. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2013.
- Чулков, П.В. Материалы курса “Уравнения и неравенства в школьном курсе математики”: Лекции 5-8./ П.В. Чулков. – М.: Педагогический университет “Первое сентября”, 2010.
- Егерев, В.К. Сборник задач по математике для поступающих во втузы: учеб. пособие/ В.К. Егерев, Б.А. Кордемский, В.В. Зайцев и др.; Под ред. М.И. Сканави. – М.: “Столетие”, 1997.
📹 Видео
Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Как решать тригонометрические неравенства?Скачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Решение тригонометрических уравнений и их систем. Практическая часть. 10 класс.Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрия в ЕГЭ может быть простойСкачать

Графический способ решения систем тригонометрических уравнений . Часть 12 .Скачать

Решение тригонометрических уравнений. 10 класс.Скачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Решение тригонометрических неравенств. 10 класс.Скачать