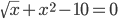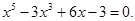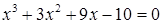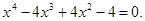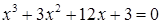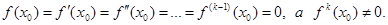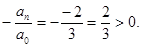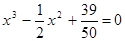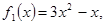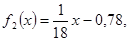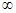Решение трансцендентных уравнений методом половинного деления

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i -ом шаге.
ξ_i=½(b_i+a_i), i=0,1.
где a₀=a; b₀=b; a_i;b_i — границы подынтервалов, в которых f(a_i)f(b_i) 0 мы ни задали, всегда можно найти такое n , что ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.

Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].

• Решение
• Видео решение

Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3

Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.

Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн

Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.

Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

— применить умения отделять корни алгебраических уравнений;

— применить умения решать алгебраические уравнений приближенными методами (метод половинного деления, метод хорд, метод касательных);

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

1. Методом итераций решить уравнение с точностью до 0,001

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

2. Методом итераций решить с точностью до 0,001 уравнение.

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

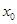
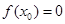
Число из области определения функции называется корнем уравнения , если .

Процесс нахождения корней уравнения распадается на несколько этапов:

1) определяются границы интервала, в котором находятся все корни уравнения ;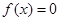

2) устанавливаются возможно малые промежутки, в каждом из которых содержатся ровно один корень.

3) каждый из корней вычисляется с заданной точностью.

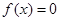
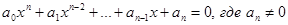
К сожалению, определение в общем виде границ интервала, в котором находятся все корни уравнения , можно дать только для алгебраического уравнения в каноническом виде, т.е. для уравнения вида:

(1)

В дальнейшем будем находить действительные корни алгебраических уравнений.

Теорема 1 (основная теорема алгебры).

Уравнения вида (1) имеет ровно n корней, действительных или комплексных, если корень кратности k считать за k корней.

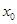
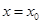
Число называется корнем кратности k уравнения (1), если при обращается в нуль сама функция и ее производные до ( k -1 )-го порядка включительно, т.е.

Корень кратности 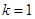называется простым.

1) Число действительных корней уравнения (1) четной степени с действительными коэффициентами всегда четно (в том числе и может равняться нулю).

Если кроме этого 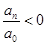, то уравнение четной степени имеет, по крайней мере, два действительных корня разного знака.

2) Уравнение (1) нечетной степени имеет по крайней мере один действительный корень того же знака, что и « ».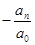

Теорема 3 (теорема Декарта).

Число положительных корней уравнения (1) равно или на четное число меньше числа перемен знака в ряду коэффициентов 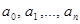уравнения. Так как при замене «х» на «-у» корни уравнения (1) меняют знаки, то с помощью этой теоремы можно оценить и число отрицательных корней.

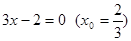
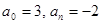
1. В уравнении нечетной степени коэффициенты и

Кроме этого, число перемен знаков равно 1.

Следовательно, по теоремам 2 и 3, оно имеет один действительный положительный корень.

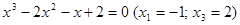
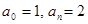
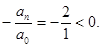
2. В уравнении нечетной степени коэффициенты и Следовательно по теореме 2, оно имеет по крайней мере один действительный отрицательный корень.

Число перемен знаков в данном уравнении равно двум, следовательно, по теореме 3, оно имеет либо два, либо 0 положительных действительных корней.

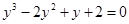
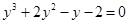
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение, или , или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный отрицательный корень.

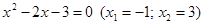
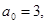
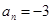
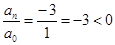
3. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет два действительных корня разного знака.

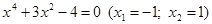
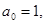
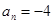
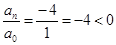
4. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет по крайней мере два действительных корня разного знака.

Число перемен знаков в данном уравнении равно 1, следовательно, по теореме 3, оно имеет один положительный действительный корень.

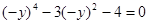
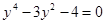
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный корень.

Дадим теперь формулировку теоремы, позволяющей достаточно грубо определять границы интервала, в котором находятся все действительные корни уравнения (1).

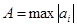
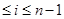
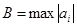
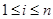
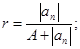
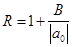
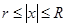
1) Если , где 0 ; , где , и , то .

2) Все положительные действительные корни уравнения находятся в промежутке , а все отрицательные действительные корни уравнения (1) находятся в промежутке .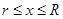

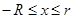
Если непрерывная и дифференцируемая функции , определяющая алгебраическое уравнение , на концах отрезка принимает значения разных знаков, т.е. , и ее первая производная сохраняет знак внутри этого отрезка, но на находится ровно один действительный корень данного уравнения.

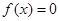
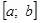
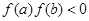
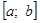
Замечание. Для алгебраических уравнений (1), степень которых больше трех, трудно аналитически находить интервалы знакопостоянства функции . Поэтому для нахождения возможно малых промежутков, содержащих ровно один действительный корень можно на практике использовать следующие способы:

1) средствами машинной графики функция представляется на дисплее и приближенно определяются возможно малые промежутки, содержащие ровно один корень (т.е. промежутки содержащие одну точку пересечения графика функции с осью Ох);

2) если график функции построить трудно, то формируют простые функции и , такие, что уравнение преобразуется в виде = . Затем строятся графики функций у= и y = и приближенно определяются промежутки, содержащие абсциссы точек пересечения этих графиков.

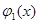
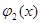
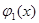
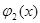
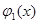
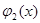
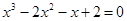
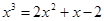
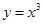
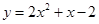
Так, например, уравнение можно преобразовать к виду и затем построить графики функции и .

Начиная третий этап, дадим формулировку теоремы, позволяющей оценивать погрешность приближенного решения.

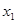
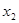
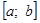
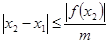
Если точный, а — приближенный, корни уравнения (1), принадлежащие одному и тому же промежутку , то справедливая оценка: , где m – наименьшее значение модуля производной функции на промежутке .

Графически решить уравнение x ln ( x )=1 .

Решение. Запишем исходное уравнение в виде: , т.е. и . Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых и .

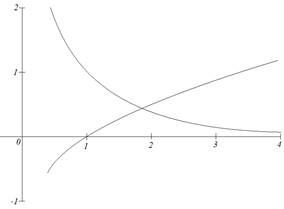
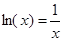
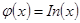
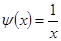
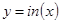
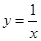
Теперь построим графики функций и определим интервал изоляции корня.

Аналитически отделить корни данного алгебраического уравнения, используя теорему Штурма:

,

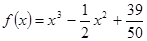
Построим таблицу для подсчета смены знаков:

—

Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления

Решение трансцендентных и алгебраических уравнений

Трансцендентное уравнение — это уравнение, содержащее трансцендентные функции (показательные, логарифмические, тригонометрические и обратные тригонометрическим) от неизвестного (переменного).

.

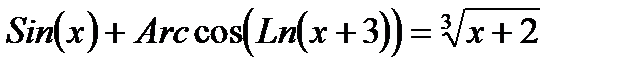
Алгебраическим уравнением степени n, в свою очередь, называется уравнение вида

где , . — некоторые вещественные числа, причем .

Трансцендентные и алгебраические уравнения, в общем случае, можно решать только приближенно. Поэтому особое значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Постановка задачи

Пусть дано уравнение , где функция F(x) определена и непрерывна в некотором конечном или бесконечном интервале a

Пример. Нижеприведенная программа находит отрезок, на котором уравнение имеет изолированный корень.

Var A,B,x1,x2,h:Real; i:Integer;

Writeln(’Введите координаты отрезка A,B’);

Поэтому, если для алгебраического уравнения мы нашли n отрезков, на которых функция меняет знак, то мы изолировали все корни.

Для выполнения второго этапа — нахождения изолированного корня с заданной точностью — применяют специальные методы вычислительной математики. Данные методы можно условно разбить на две группы — первые получают решение в виде предела последовательности отрезков, содержащих изолированный корень. Ниже представлены два подобных метода — метод половинного деления и метод хорд. Вторые представляют корень уравнения в виде предела последовательности приближенных корней разной (увеличивающейся) степени точности. Примеры методов — метод итераций, метод Ньютона, модифицированный метод Ньютона и метод секущих.

Необходимо также отметить, что большинство из приведенных методов работают только для корней кратности 1. Если на отрезке существует корень кратности 2 или большей, то для их нахождения следует использовать метод Ньютона с параметром.

Метод половинного деления

Пусть дано уравнение

, (1.1)

где функция F(x) определена и непрерывна на отрезке , причем .

Метод половинного деления заключается в следующем. Делим отрезок пополам. Вычисляем . Если , то с — корень уравнения. Мы получили решение задачи, и работа прекращается. В противном случае, выбираем в качестве очередного один из отрезков или , на границах которого функция имеет значения разных знаков (т.е. именно в нем остался корень). Этот отрезок переобозначаем через , снова делим пополам и т.д. Данный процесс повторяем до тех пор, пока длина очередного отрезка не станет меньше заданной погрешности Eps (например, Eps=0.001). В этом случае, в качестве приближенного значения корня берут середину последнего отрезка .

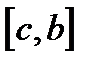
Проверим сходимость метода. Последовательность — невозрастающая ограниченная снизу последовательность. Следовательно, она имеет предел . Аналогично, последовательность является неубывающей ограниченной сверху последовательностью и поэтому имеет свой предел . Из условий и существования двух пределов получаем, что A=B. Причем, из условия , переходя к пределу при , получаем, что и, следовательно, . Итак, метод половинного деления сходится к корню уравнения.

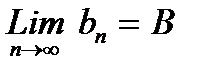
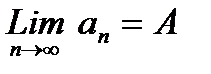
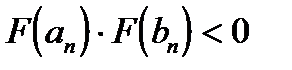
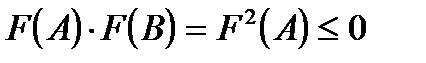
Пример. Ниже приведен фрагмент программы, выбирающий очередной отрезок для метода половинного деления.

Writeln(’На отрезке от ’,A:12:7,’ до ’,B:12:7,

Метод итераций

Пусть дано уравнение

. (1.4)

Умножим обе части уравнения на некоторую функцию [2], и прибавим к обеим частям уравнения. Получим тождественное уравнение

. (1.5)

. (1.6)

Следовательно, от уравнения (1.4) мы переходим к тождественному уравнению (1.7)[3]:

. (1.7)

Выберем каким-нибудь образом грубое приближенное значение корня (например, один из концов отрезка). Назовем его начальным приближением. Подставим в правую часть нового уравнения (1.7) и вычислим очередное приближение . Далее подставим в правую часть уравнения (1.7) и вычислим . Будем повторять данный процесс. В результате получим последовательность значений:

, где . (1.8)

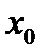
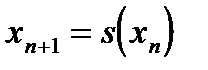
Если данная последовательность сходится, т.е. у нее существует предел , то, перейдя к пределу, получим и . Следовательно, — корень уравнения. Т.к. на компьютерах практически невозможно проводить бесконечно большое количество операций (т.к. это потребует бесконечно большого количества машинных часов), то точное значение корня вычислить, в общем случае, нельзя. Но приближенное значение корня можно вычислить с любой требуемой точностью.

Как определить, сколько раз необходимо выполнить итерационную формулу 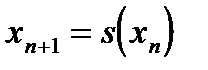, и с какой точностью будет найден приближенный корень? На практике задают погрешность Eps (обычно Eps=0.001) и говорят, что требуемая точность достигнута при выполнении одного из условий: или . Данные условия окончания счета принято называть критериями сходимости. Иногда в качестве критерия пытаются использовать выполнение определенного заранее заданного количества итераций[4]. Но указанный третий подход на практике является неверным и может быть использован только в качестве защиты от зацикливания программы при неверных исходных параметрах.

Теоретическим обоснованием метода итераций служит следующая теорема.

Теорема. Пусть функция определена и дифференцируема на отрезке , причем все ее значения . Тогда, если существует рациональное число q, такое что для , то 1) Процесс итерации для сходится независимо от начального значения . 2) Предельное значение является единственным корнем уравнения .

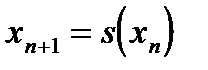
Примечание. На практике обычно берут константу и используют итерационный процесс . Следовательно, и метод итераций сходится при условии .

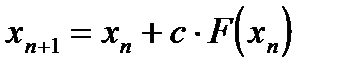
Пример. Решить уравнение .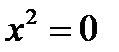

Берем const . Получаем .

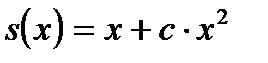
Далее, .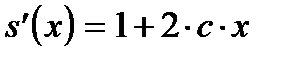

Согласно условиям теоремы и примечания имеем .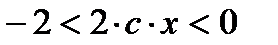

Т.к. для любого отрезка, содержащего корень уравнения , данное условие выполняться не будет (невозможно подобрать const c), то теоретически метод итераций для этого примера сходиться не будет при любом начальном приближении. Однако на практике возможно подобрать коэффициенты метода итераций для его сходимости. Например, при и метод не сходится. При и метод сходится при погрешности Eps=0.0001 и уже не сходится при Eps=0.00001.

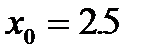
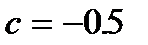
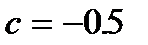
Пример. Решить уравнение .

В качестве отрезка с корнем возьмем .

Берем const c. Получаем .

Далее, .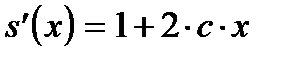

Согласно условиям теоремы и примечания имеем .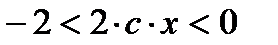

При 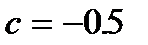вышеприведенное неравенство верно для заданного отрезка и метод итераций сходится при любом начальном приближении из отрезка .

Пример. Ниже приведен фрагмент программы, реализующий метод итераций. Для реализации последовательности приближений используется цикл с постусловием Repeat . Until. Считается, что все нужные переменные и функция F(x) ранее определеныи им заданы нужные значения.

📺 Видео

Метод половинного деления. ДихотомияСкачать

Метод половинного деленияСкачать

12й класс; Информатика; "Численные методы. Метод половинного деления"Скачать

Решение нелинейного уравнения методом половинного деления (программа)Скачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Урок 10. C++ Метод половинного деленияСкачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

Решение уравнений (метод дихотомии) на C#Скачать

7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать

Метод половинного деления - ВизуализацияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Численные методы (1 урок)(Решение нелинейных уравнений. Метод дихотомии. Python)Скачать

Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать

Решение нелинейного уравнения методом половинного деления (дихотомии)Скачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Решение нелинейного уравнения методом деления отрезка пополамСкачать

1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать