Решение системы уравнений в octave (7 видео)

IT Novella

После нажатия клавиши на экране появится результат выполнения команды

Функция rand позволяет генерировать случайные числа из нтервала (0,1).

Если функция вызывается без аргументов, то будет создано случайное число.

Если функция имеет один аргумент rand(m), то будет создана квадратная матрица размерности mхm.

Если передать два аргумента rand(m,n), то будет создана матрица размерности $ m times n $

В теории линейной алгебры выделяют специальные виды матриц.

Создать такие матрицы в Octave позволяют следующие функции:

ones(m),ones(m,n)
Функция генерирует матрицу с элементами 1 (количество аргументов трактуется аналогично eye).octave:18> = ones(2)

zeros(m), zeros(m,n)
Функция генерирует нулевую матрицу (количество аргументов трактуется аналогично eye).octave:29> Z = zeros(2)

diag(v, k)
Функция генерирует диагональную матрицу с элементами вектора v на диагонали k. Аргумент k выступает в качестве опции:k=0 означает главную диагональ, при k > 0 элементы вектора v ставятся на k-ую диагональ выше, а при k D = diag([1 2 3])

Содержание

Возможности СКМ Octave
Система компьютерной математики Octave
Системы компьютерной математики
Простейшие операции
Рассмотрим пример
Элементарные математические функции
Экспоненциальные функции
Условный оператор
Матрично-векторные вычисления
Создание матриц
Возможности СКМ Octave
Высшая математика командной строки — GNU Octave
Догнать и перегнать MATLAB
Установка
Операции с матрицами
Функции и переменные
Графический интерфейс
Что-же дальше?
Рекомендуется к прочтению
Решение системы линейных уравнений
📸 Видео

Возможности СКМ Octave

GNU Octave — высокоуровневый язык программирования, предназначенный прежде всего для численных расчётов. Он предоставляет удобный интерфейс командной строки для численного решения линейных и нелинейных задач, а также для выполнения других численных экспериментов. Кроме того, GNU Octave — свободно распространяемое программное обеспечение.

Видео:Решение двух систем уравнений в MatLabСкачать

Система компьютерной математики Octave

Системы компьютерной математики

Система компьютерной алгебры (computer algebra system, CAS) — программное приложение для символьных вычислений,

т.е. для выполнения преобразований и работы с математическими выражениями в аналитической (символьной) форме.

GNU Octave

GNU Octave — это свободно распространяемый язык программирования высокого уровня, ориентированный на проведение численных расчетов, и по сути являющийся альтернативой коммерческому пакету MatLab.

Простейшие операции

Простейшие арифметические операции в Octave выполняются с помощью следующих операторов:

Рассмотрим пример

Решить систему линейных алгебраических уравнений:

Для решения СЛАУ в окне интерпретатора Octave последовательно введём следующие команды:

Элементарные математические функции

Экспоненциальные функции

Примеры применения экспоненциальных функций:

Целочисленные функции

Примеры работы с целочисленными функциями:

Комплексные числа

Ввод комплексного числа производится в формате:

действительная часть + i * мнимая часть

действительная часть + j * мнимая часть

Примеры записи комплексных чисел в Octave

Функции работы с комплексными числами

Примеры использования функций

Основные операторы в Octave

Условный оператор

Обычный условный оператор имеет вид:

Обычный оператор if работает по следующему алгоритму:

если условие истинно, то выполняются операторы1, если ложно — операторы2.

Рассмотрим работу условного оператора на примере.

Пример:даны вещественные числа x и y. Определить принадлежит ли точка с координатами (x;y) заштрихованной части плоскости.

Текст программы и результат её работы

Оператор альтернативного выбора

Оператор switch

Оператор switch работает следующим образом: если значение параметра равно значение1, то выполняются опреаторы1, иначе если параметр равен значение2, то выполняются операторы2. В противном случае, если значение параметра совпадает с значение3, то выполняются операторы3 и т.д. Если значение параметра не совпадает ни с одним из значений в группах case, то выполняются операторы, идущие после служебного слова otherwise.

Рассмотрим использование оператора switch на примере:

Вывести на экран название дня недели, соответствующее заданному числу D, при условии, что в месяце 31 день и первое число — понедельник.

Матрично-векторные вычисления

Создание матриц

Любую матрицу или вектор с заданными элементами в Octave можно создать путем перечисления

этих элементов в квадратных скобках ([ ]), разделяя столбцы пробелом или запятой, строки

знаком ”точка с запятой”

octave:1>A=[1 3 5; 2 4 6]

После нажатия клавиши на экране появится результат выполнения команды

Функция rand позволяет генерировать случайные числа из нтервала (0,1).

Если функция вызывается без аргументов, то будет создано случайное число.

Если функция имеет один аргумент rand(m), то будет создана квадратная матрица размерности mхm.

Если передать два аргумента rand(m,n), то будет создана матрица размерности $ m times n $

В теории линейной алгебры выделяют специальные виды матриц.

Создать такие матрицы в Octave позволяют следующие функции:

ones(m),ones(m,n)
Функция генерирует матрицу с элементами 1 (количество аргументов трактуется аналогично eye).octave:18> = ones(2)

zeros(m), zeros(m,n)
Функция генерирует нулевую матрицу (количество аргументов трактуется аналогично eye).octave:29> Z = zeros(2)

diag(v, k)
Функция генерирует диагональную матрицу с элементами вектора v на диагонали k. Аргумент k выступает в качестве опции:k=0 означает главную диагональ, при k > 0 элементы вектора v ставятся на k-ую диагональ выше, а при k D = diag([1 2 3])

Возможности СКМ Octave

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Высшая математика командной строки — GNU Octave

Как я и обещал, перехожу от обзора программ замены калькулятора к более серьезным инструментам. Если помните схему из предыдущего поста, то во второй категории находились табличные: OpenOffice / LibreOffice сотоварищи. Эту партию мы можем смело пропустить, так как к командной строке она не относится, к тому же, среди читателей Хабра трудно найти человека, который бы в них не разбирался. Поэтому перехожу сразу к третьей категории.

Специализированные математические программы, уровень студент+

На первом месте в этом списке находится Octave , и это не случайность. Исследователи из Университета Мэриленда в США провели сравнительный анализ математических вычислений, используя MATLAB, Octave, SciLab и FreeMat в простом сценарии и в сложном. В первом случае решали систему линейных уравнений а в втором — конечно-разностную дискретизацию уравнения Пуассона в двухмерном пространстве. Основной вывод — GNU Octave справляется с задачами лучше остальных открытых математических пакетов, демонстрируя результат (страницы 23 и 25) сопоставимый с матлабовским.

Но сначала немного исторического контекста, чтобы понять, как закалялись математические программы с открытыми исходниками.

Видео:octave_01_intro.ogv (in Russian)Скачать

Догнать и перегнать MATLAB

Так сложилось, что коммерческие программы прибежали и первыми застолбили поляну математических вычислений. Уже с конца 1970-х гг. создатель языка программирования Клив Моулер распространяет MATLAB в университетах США, а в 1984-м вместе с двумя компаньонами переписывают его с Фортрана на Си и создают компанию The MathWorks. Примечательно, что ранние версии распространялись с открытым исходным кодом.

Это было-было, а MATLAB , каким мы его знаем сегодня — это ЯП высокого уровня с поддержкой 2D / 3D графики, разнообразными математическими функциями, интерактивной средой программирования, численных расчетов и решения задач. Внешние интерфейсы позволяют ему интегрироваться со сторонними приложениями и языками программирования. Более 1 000 000 инженеров и ученых по всему миру используют MATLAB и платят за это солидную денежку.

С большим опозданием в игру включаются программы с открытыми исходниками. Только в 1990-х появляются математические пакеты GNU Octave, Scilab и вступают в конкуренцию с лидером вычислительного программирования.

Задуманный изначально как программное пособие для проектирования химического реактора и названный в честь профессора химии Октава Левеншпиля, преподававшего автору математического пакета, Octave призван был заменить студентам Техасского Университета сложный в отладке Fortran . Версия 1.0 вышла в свет 17 февраля 1994 г. Проект стабильно развивается, и в июле нынешнего года зарелизился Octave 4.0.3 . Ждем ебилдов .

Основной миссией Octave была, и в обозримом будущем скорее всего так и останется, быть годной заменой MATLAB так же, как OpenOffice/LibreOffice замещает MS Office для тех, кто умеет считать копейку. Собственно, для этого Octave имеет совместимый с MATLAB синтаксис и набор функций. Более того, несовместимость с MATLAB считается багом, однако софтверная Фемида уже имеет подобный прецедент, и это не считается нарушением копирайта. В этой связи, можно считать Octave программным клоном. Правда о полной совместимости пока говорить не приходится, но работа в этом направлении не прекращается.

Octave написан на C++ , используя стандартную библиотеку шаблонов, имеет интерактивный командный интерфейс, поддерживает расширения — динамически загружаемые модули на родном языке или на C, C++, Fortran и др. Так же как и MATLAB , в алгебраических вычислениях Octave использует библиотеки Basic Linear Algebra Subroutines (BLAS) и Linear Algebra Package (LAPACK).

Видео:Матричный метод решения систем уравненийСкачать

Установка

Установка Octave в Linux ничем не отличается от установки других программ. На Gentoo Linux запускаем:

Дебианщики делают то же самое с помощью apt .

Для SUSE и Arch тоже все очень просто, а вот пользователям Красной Шапки и CentOS придется чуток повозиться. Попытка установить Octave легким движением кисти завершается ошибкой, пакет в репозитариях не найден.

Благо, есть обходной путь. Нужно сперва установить пакет epel-release.

И только после этого yum install octave сработает.
Наконец, все готово и программа установлена.

Видео:octave_03_matrix.ogv (in Russian)Скачать

Операции с матрицами

Не будем терять время и делать операции, которые можно повторить с помощью bc и awk , о ктоторых речь шла в прошлый раз. Поиграемся немного с матрицами.

Сперва простое транспонирование матрицы:

Попробуем решить систему линейных уравнений:

Вбиваем матрицу A, вектор b и решаем уравнение Ax = b в матричном виде

Находим детерминант и собственные значения матрицы.

Комплексные числа тоже поддерживаются в вычислениях.

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Функции и переменные

В Octave переменные и функции создавать гораздо проще, чем, к примеру, в Java или C. На примере матриц, мы уже видели как объявлять переменные. Создания новой функции имеет следующий синтаксис

Как правило, новую функцию создают либо в отдельном файле, либо в скрипт-файле Octave
до первого ее вызова. Если предполагается использовать пользовательскую функцию в разных скрипт-файлах, то, конечно, предпочтительно создать ее в отдельном файле. В GNU Octave файлы с функциями имеют расширение .m и загружаются автоматически. Имя файла должно строго совпадать с именем функции.

Напишем функцию для решения квадратичного уравнения ax² + bx + c = 0

Видео:Gnu Octave в физике и технике.Скачать

Графический интерфейс

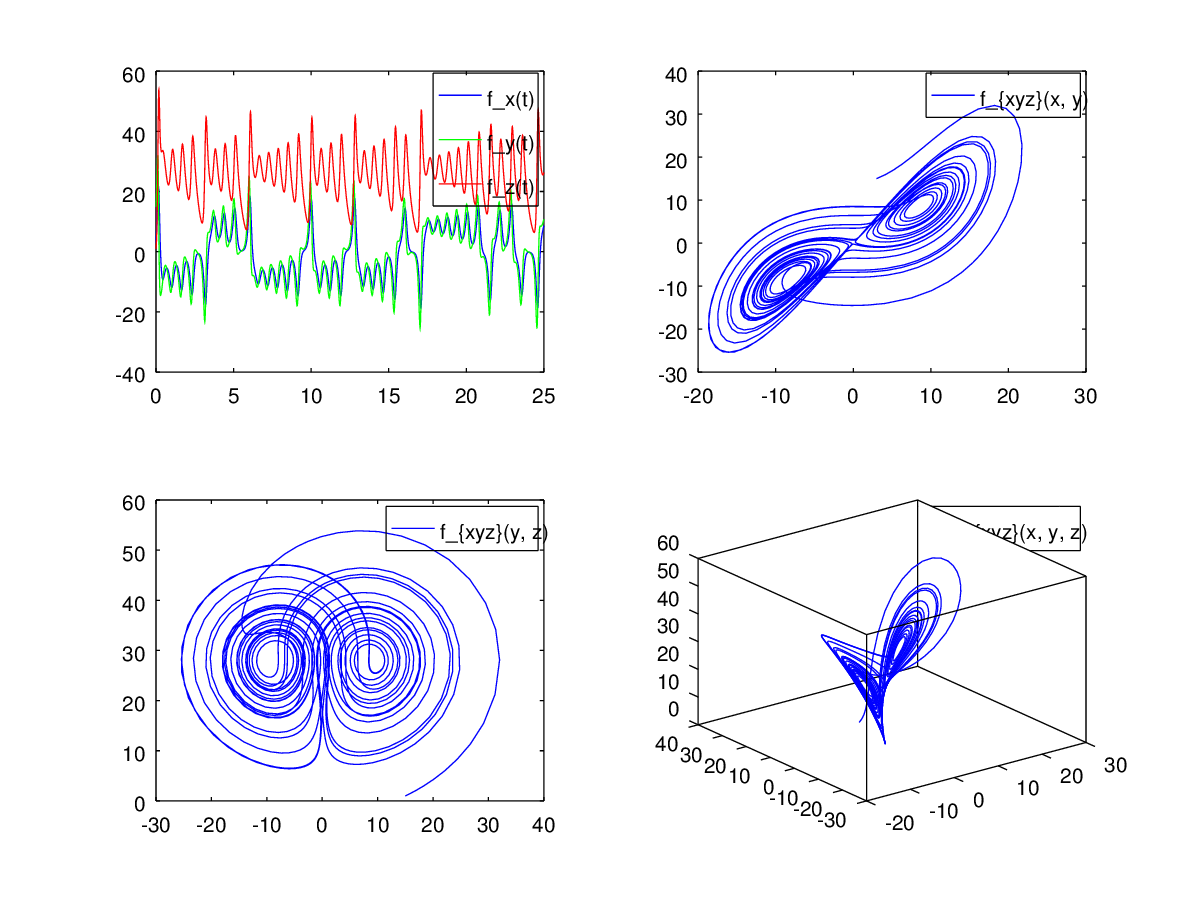
Вообще-то, мы тут за математику командной строки гутарим, но пока непонятно как вывести на экран график функции. Впрочем, никакого секрета тут нет — для этих целей используется Gnuplot . Так можно изобразить Аттрактор Лоренца, установив дополнительный пакет odepkg .

Наиболее удобной графической оболочкой для работы с Octave является программа QtOctave . Последняя уже стабилизировалась и включена в состав пакета с момента выхода Octave 4.0 .

Видео:Решение системы уравнений методом ГауссаСкачать

Что-же дальше?

Может возникнуть вопрос: а зачем вообще нужны открытые математические пакеты? Офисные приложения нужны всем, но ведь далеко не каждому необходимо сидя дома решать уравнения Пуассона, с помощью преобразования Лапласа. Для ВУЗ-ов MATLAB стоит значительно дешевле, нежели для физических лиц и коммерческих организаций. Коммерческие организации, если будет нужно, найдут денежные средства, а обычные люди пусть занимаются математикой в университетах или считают столбиком.

Конечно же, это ошибочное мнение. Научные расчеты, выполненные с использованием открытого ПО имеют дополнительный «уровень защиты», ведь при желании любой может повторить прогнать те же самые расчеты и проверить валидность результатов. Те же самые вычисления, выполненные на дорогущем ПО, частично отсекают возможность проверки результатов. Проблема на самом деле гораздо шире (английский текст) и дело не только в открытых или проприетарных математических программах. Не секрет, что научные журналы как правило не требуют от авторов предоставить данные и методику, достаточные для гарантированного повтора результатов эксперимента, проверки модели. Особенно часто этим грешат экономисты и финансисты, попросту засекречивая свои данные. Проверка расчетов и выводов среди выборки из массива статей с «засекреченными» данными дала неожиданные результаты (английский текст). Наука, как и софт, должна быть открытой, вот почему открытые математические пакеты имеют ценность для всего общества.

Решение системы линейных уравнений

Двухмерные графики >>

Решение системы линейных уравнений. Исходная система уравнений. Шаг 2. Задать матрицы в Octave >> A=[1 1 -1; 2 3 -4; 7 -1 -3]; >> b=[6; 21; 6]; Шаг 3. Решить систему >> x=Ab x = 5.0753e-16 3.0000e+00 -3.0000e+00. Шаг 4. Проверить решение >> disp(A*x); 6 21 6 Альтернативные способы >> x=inv(A)*b; >> x=A^(-1)*b; . .

Слайд 6 из презентации «Основы работы в GNU Octave»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Основы работы в GNU Octave.pptx» можно в zip-архиве размером 1358 КБ.

«Урок в школе» — Форматирование. Творческий уровень. Дидактические цели уроков. Урок – основная форма организации учебного процесса. Контроль и оценка планируемых результатов. Осознанность по отношению к цели деятельности. Предоставляемая учащимся свобода выбора учебных действий. Основной этап. Доказательный уровень.

«Я иду на урок» — Литература. Я просыпаюсь. Значит скорость можно найти по формуле V = S : t Моя скорость равна 5 км/ч. Мы решаем задачи и примеры. Мы учим параграфы и слушаем объяснения учителя. От моего дома до школы 5 км. Русский язык. Я прихожу в школу. Путь вычисляется по формуле S = V · t. У Лукоморья дуб зелёный, Златая цепь на дубе том.

«Этапы урока» — Схема моделирования учебного занятия. Рефлексия. Методы обучения. Средства. С чего начинать? Результативность урока. Содержание урока. Целеполагание. Какое задать Д/З. Здоровьесберегающее пространство урока. Фоупд. Этапы урока. Цель и задачи: 1 2 3. Аспекты цели урока: “Добрый день, друзья! Тип учебного занятия.

«Конспекты уроков» — Животные. Рыбы. Конспект урока. Формы растений. Лыжный поход. Сосна. Сыроежки. Решение задач. Сколько конфет осталось в коробке?. Задачи для устного счета. Марки. Амфибии. Конспект урока по математике. Ящик. Растения. Карандаши. Млекопитающие. Птицы. Кусок мыла. Уроки математики и природоведения. Сколько деревьев на двух сторонах улицы?.

«Мыслительная деятельность на уроке» — Модель выпускника начальной школы. Развитие мыслительной деятельности на уроке. Этапы урока. Урок. Важнейшая задача цивилизации. Условия использования приемов. Приемы активизации мыслительной деятельности. Мягкий знак. Т.Эдисон. Тема-вопрос.

«Урок производственного обучения» — Самооценка Взаимооценивание Экспертная оценка Рейтинговая оценка Система зачетов. Основной этап. Актуальность вопроса. Формы организации учебно-производственной деятельности обучающихся на уроке ПО. Вводный этап. Новое поколение стандартов разработаны на модульно- компетентностной основе. Дифференцированный процесс обучения.