Решение системы уравнений в маткаде solve (7 видео)

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Содержание

Использование метода Given — Find:
Использование метода Solve:
Решение системы уравнений в маткаде solve
5.1 Решение алгебраических (и других) уравнений и систем.
5.2 Решение дифференциальных уравнений и систем (задача Коши и граничные задачи).
5.3 Задание.
5.1 Решение алгебраических (и других) уравнений и систем.
Линейные алгебраические уравнения.
Квадратные уравнения и алгебраические уравнения высших порядков.
Иррациональное уравнения (уравнения с радикалами).
Решение системы уравнений в маткаде solve
📹 Видео

Видео:MathCAD Решение системы уравненийСкачать

Использование метода Given — Find:

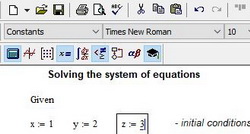
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

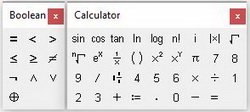
Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

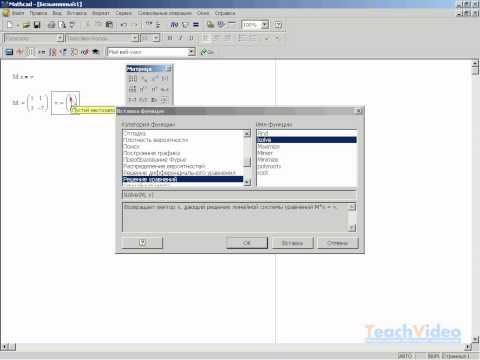
Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

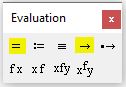
Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Видео:Ключевое слово solve в MathCAD 14 (26/34)Скачать

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

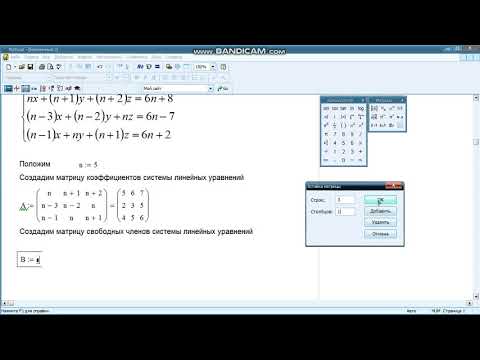
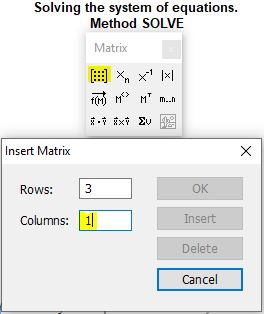
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Решение системы уравнений в маткаде solve

Электронный курс по MathCAD

Лекция 5.
Решение уравнений и систем.

5.1 Решение алгебраических (и других) уравнений и систем.

5.2 Решение дифференциальных уравнений и систем (задача Коши и граничные задачи).

5.3 Задание.

5.1 Решение алгебраических (и других) уравнений и систем.

Линейные алгебраические уравнения.

Определение: Уравнение вида ax+b=0 с заданным базовым множеством G_x, a из G_a , b из G_b называется линейным уравнением.

Этапы решения при помощи Mathcad:

Ввести уравнение (знак «=» вводится при помощи комбинации [Ctrl++]).
Выделить курсором переменную, относительно которой должно быть решено уравнение.
Выбрать команду Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы).

При решении линейных уравнений (без параметров) или дробных уравнений, которые сводятся к линейным, MathCAD находит все существующие решения. Однако при этом следует правильно интерпретировать сообщения, выдаваемые системой.

Нормальный случай.

В качестве решения MathCAD выдает число — это означает,

что уравнение однозначно разрешимо (однозначное решение линейного уравнения над множеством действительных чисел, которое одновременно является областью определения этого уравнения).

Рассмотрим другой пример:

Решение системы уравнений в маткаде solve

После выполнения описанных выше действий для нахождения решения Mathcad выдает сообщение о том, что решение не найдено.

Проанализировав данное уравнение приходим к выводу, что выданное Mathcad сообщение означает, что решений нет L=.

MathCAD выдает сообщение «Решение не найдено», даже если уравнение имеет «формальное решение», которое не принадлежит области определения (смотри примеры ниже).

Многозначность.
Если в качестве решения MathCAD выдает имя переменной, это означает, что множество решений уравнения совпадает с областью определения. Однако, такие понятия, как множество решений уравнения и область определения, отсутствуют в MAthCAD и он не выписывает оболасть определения. Вы можете найти область определения, решая с помощью Mathcad систему неравенств или уравнений

Такой результат, выданный Mathcad после выполнения действий по решению уравнения, означает, что любое значение x из базового множества удовлетворяет этому уравнению, т. е. L=R.

Дробные уравнения

Команда Solve (Вычислить) из подменю Variable (Переменные) меню Symbolics (Символы)выдает множество решений: L = .

Решение 6 копируем в буфер, а затем выделяем маркером переменную x и активизируем команду Substitute (Замена) подменю Variable (Переменные) меню Symbolics (Символы) для замены переменной значением 6.

Рассмотрим другой пример:

Последнее уравнение (рисунок справа) условно эквивалентно уравнению:2x=4. Решение уравнения Mathcad: 2. Формальное решение x = 2 не входит в область допустимых значений. Mathcad выдает правильное сообщение!

Здесь также правильное решение: множество решений совпадает с областью допустимых значений L = D. Только следует учесть, что D=<R>.

Квадратные уравнения и алгебраические уравнения высших порядков.

Определение: Уравнение P(x)=0 называется алгебраическим уравнением n-го порядка, если P(x) представляет собой полином степени n, при n=2 данное уравнение называется квадратным уравнением.

При решении такого рода уравнения необходимо выполнить те же действия, что и при решении линейных уравнений.

Квадратное уравнение.

Команда Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы) дает решение в виде вектора: L= .

Иррациональное уравнения (уравнения с радикалами).

Корни (радикалы) могут вычисляться в MathCAD либо при помощи знака корня (клавиши [Ctrl+]), либо как степени (клавиша [^] с дробными показателями. Знак квадратного корня вводится нажатием клавиши []. Знак корня и квадратный корень можно найти на панели Calculator (Калькулятор). Последовательность действий при решении уравнений с радикалами та же, что и при решении рассмотренных ранее уравнений.

С точки зрения теории, между решениями уравнений с радикалами и решением алгебраических уравнений имеется два важных различия, по крайней мере, при нахождении действительных решений.

Радикалы определены не везде в действительной области. Это обстоятельство приводит к необходимости находить область определени, прежде чем решать само уравнение. Данная проблема справедливо игнорируется MathCAD, поскольку он не может знать, во множестве каких чисел (действительных или комплексных) вы намерены решать уравнение. Выход: вы можете самостоятельно найти область определения, воспользовавшись при этом возможностями MathCAD, связанными с решениями неравенств.
Вторая проблема, возникающая при решении уравнений с радикалами, имеет принципиальный характер. Функция x 2 (как и любая другая функция с четным показателем) на является инъективной (проблема главных значений). В связи с этим возведение в квадрат обеих частей уравнения, содержащего квадратные корни, не является эквивалентным преобразованием. Как всегда, при применении к обеим частям уравнения не инъективного преобразования увеличивается множество решений. В результате в него могут войти «фиктивные» решения. Как ни удивительно, MAthCAD сам производит проверку решений на «фиктивность».

Классический случай решения уравнения с радикалами.

Mathcad распознает «фиктивные» решения (которые могут возникнуть в результате неэквивалентного преобразования «возведение в квадрат») и выдает верное сообщение: Решение не найдено. L =

В приведенных примерах демонстрируется способность MathCAD находить область определения иррационального уравнения путем решения неравенств.

Уравнения с радикалами третьей степени, как и уравнения с комплексными коэффициентами, не представляют для MathCAD никакой сложности.

Уравнения с параметрами.
При решении уравнений с параметрами MathCAD ведет себя по-разному, в зависимости от того, каким образом производятся символьные вычисления — с помощью символьного знака равенства или команд меню Symbolics.

В данном примере использование палитры символьных преобразований позволяет решить уравнение (solve) и упрстить результат (simplify)

Видео:Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать

Решение системы уравнений в маткаде solve

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например: