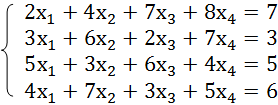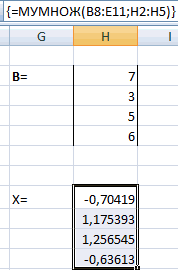Про уравнения - легко » Статьи

Решение системы уравнений в эксель через если

Обновлено
Решение системы уравнений в Microsoft Excel

Решение системы уравнений в эксель через если

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Содержание
  1. Варианты решений
  2. Способ 1: матричный метод
  3. Способ 2: подбор параметров
  4. Способ 3: метод Крамера
  5. Способ 4: метод Гаусса
  6. Решение систем уравнений в среде Microsoft Excel
  7. ХОД УРОКА
  8. I. Организационная часть.
  9. II. Повторение пройденного материала.
  10. III. Объяснение нового.
  11. IV. Практическая работа на компьютере.
  12. V. Подведение итогов.
  13. VI. Домашнее задание.
  14. Решение системы уравнений в excel
  15. Решение системы уравнений в Microsoft Excel
  16. Варианты решений
  17. Способ 1: матричный метод
  18. Способ 2: подбор параметров
  19. Способ 3: метод Крамера
  20. Способ 4: метод Гаусса
  21. Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
  22. Система линейных уравнений в Excel
  23. Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
  24. Решение уравнений в Excel методом итераций Крамера и Гаусса
  25. Решение уравнений методом подбора параметров Excel
  26. Как решить систему уравнений матричным методом в Excel
  27. Решение системы уравнений методом Крамера в Excel
  28. Решение систем уравнений методом Гаусса в Excel
  29. Примеры решения уравнений методом итераций в Excel
  30. 🔥 Видео

Видео:Решение системы уравнений в ExcelСкачать

Решение системы уравнений в Excel

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

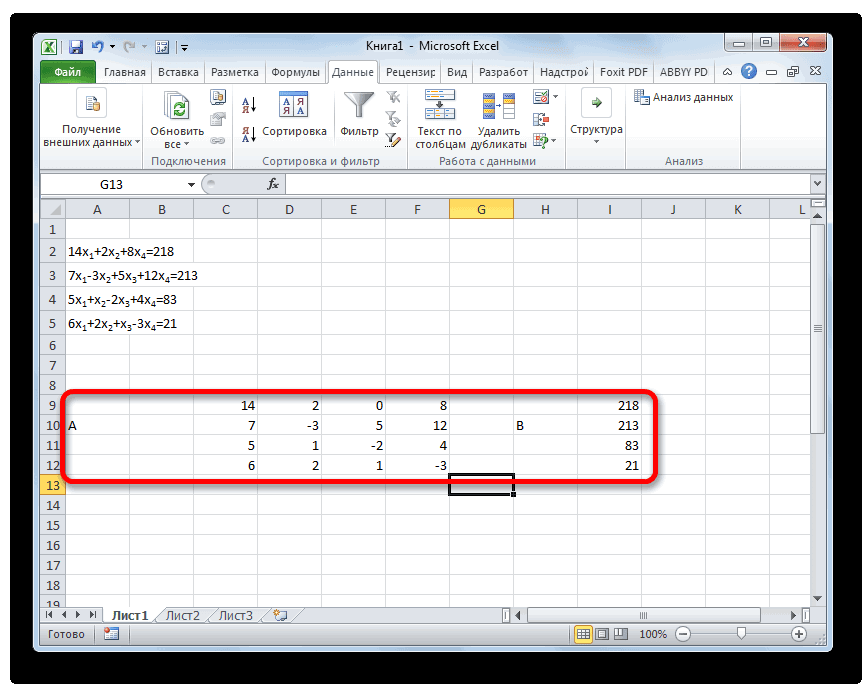
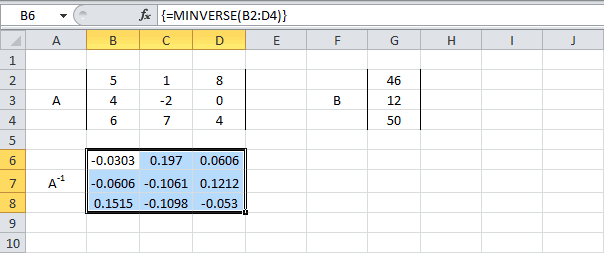
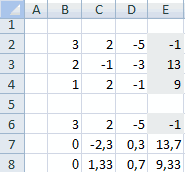
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

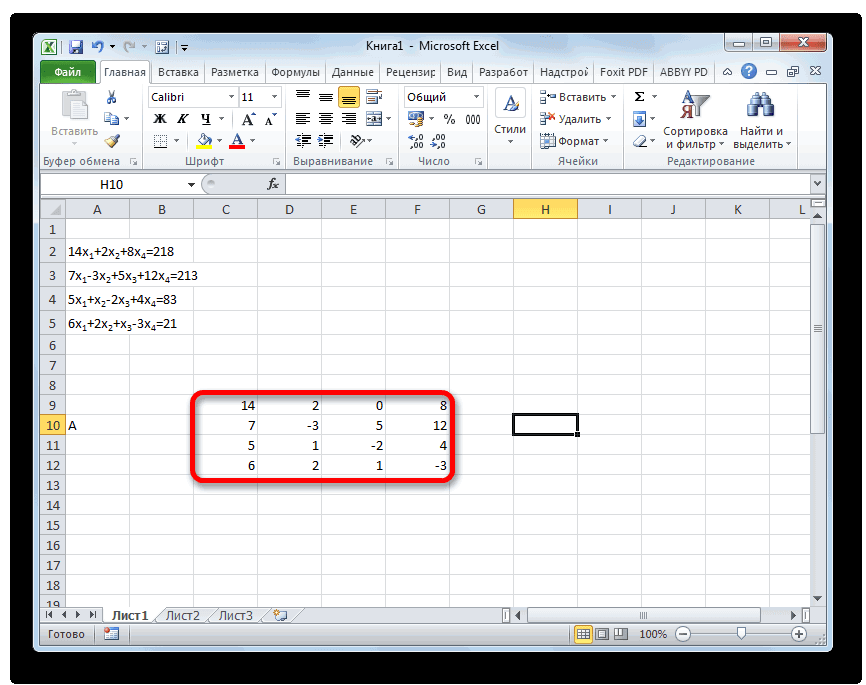
    Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

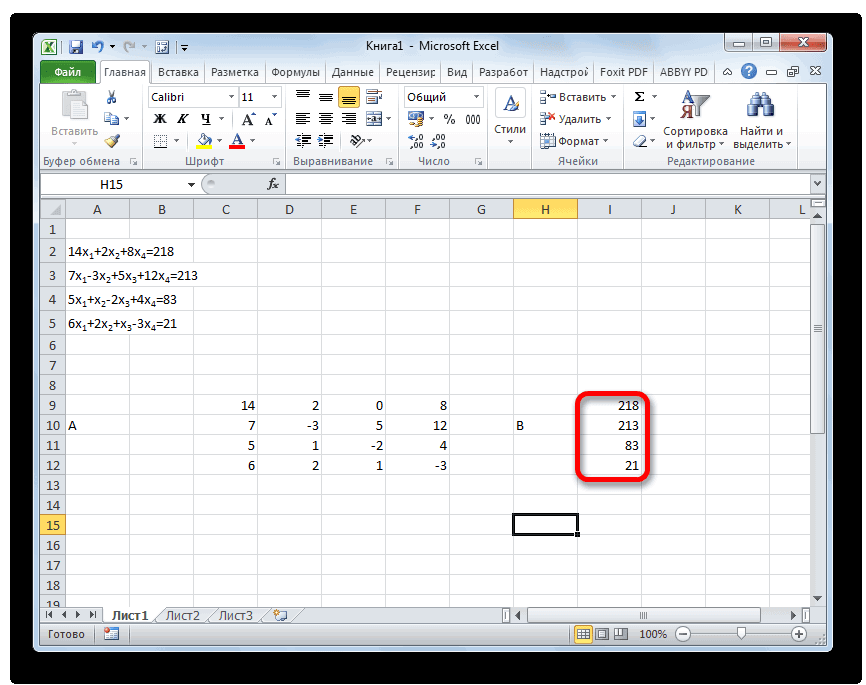
Решение системы уравнений в эксель через если

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

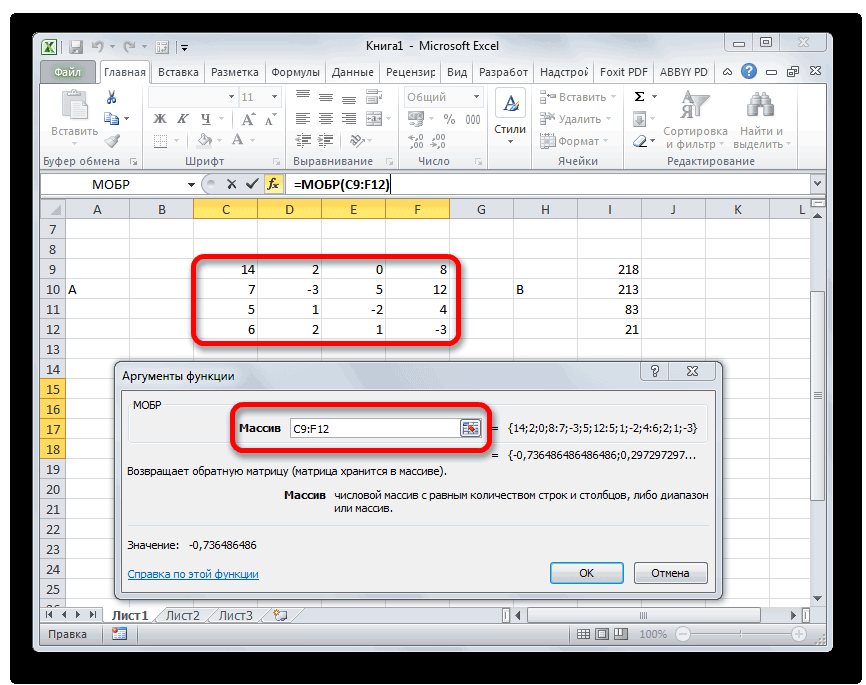
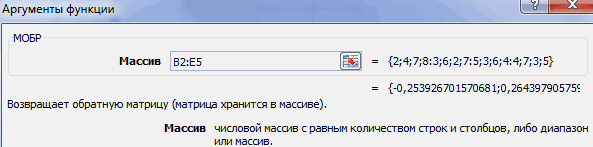
Решение системы уравнений в эксель через если

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

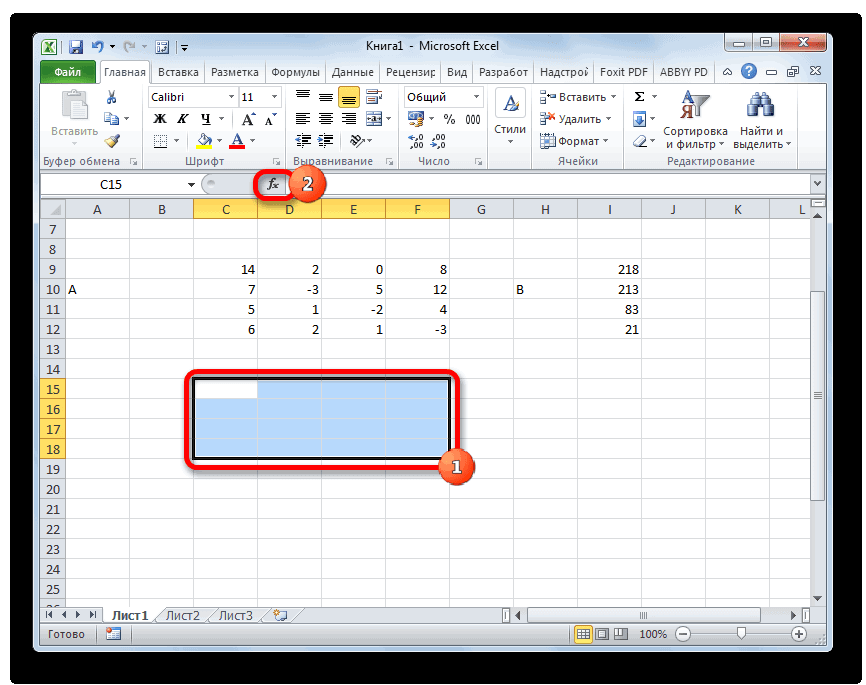
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

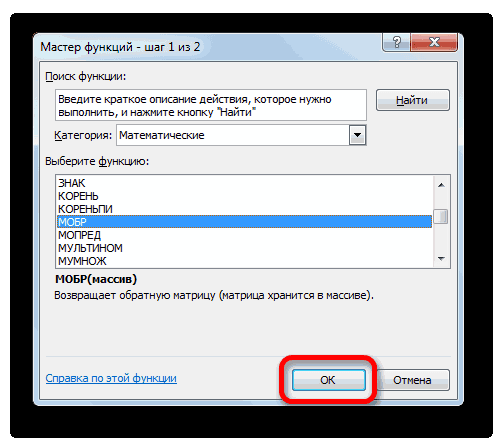
Решение системы уравнений в эксель через если

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

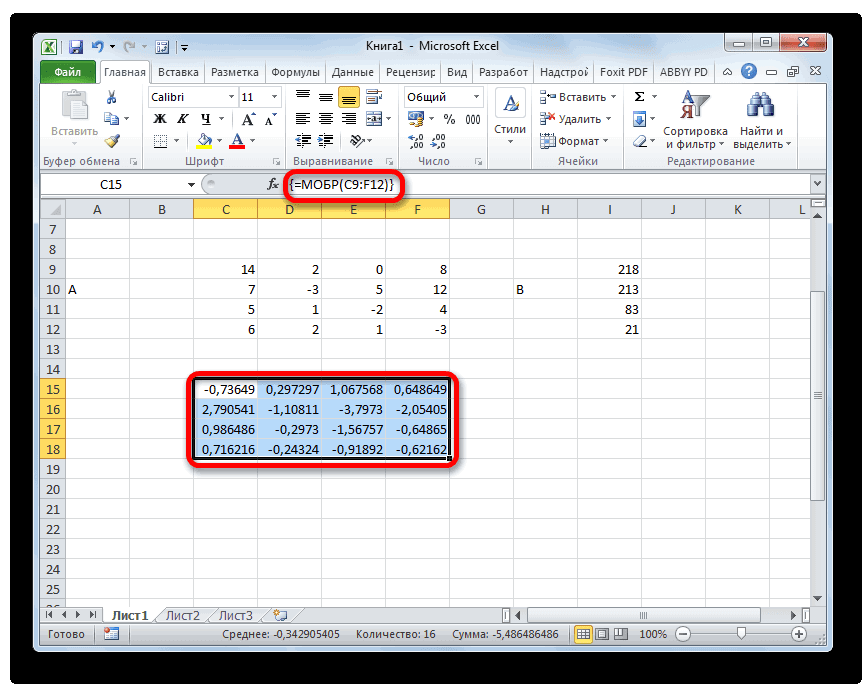
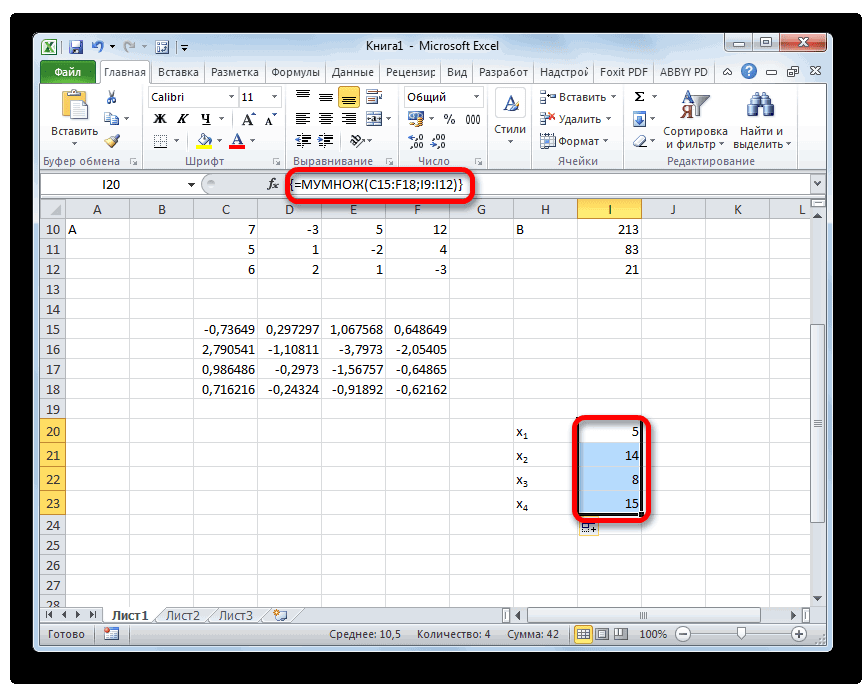
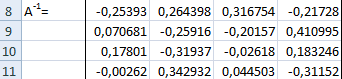
Решение системы уравнений в эксель через если

Решение системы уравнений в эксель через если

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

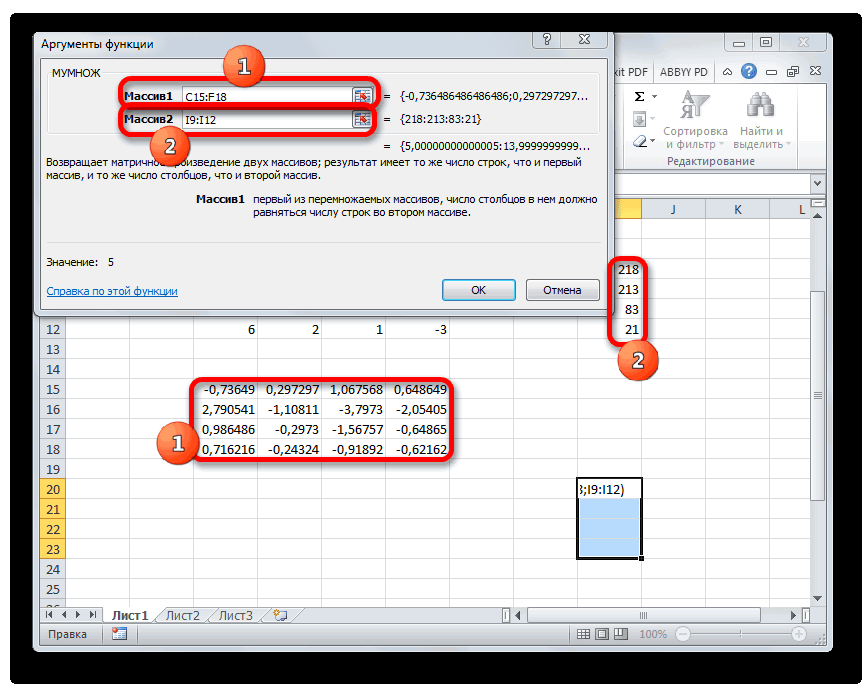
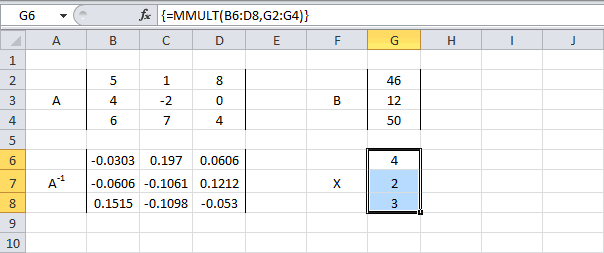
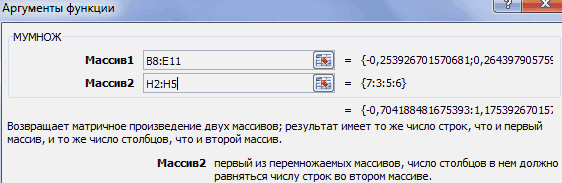
Решение системы уравнений в эксель через если

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

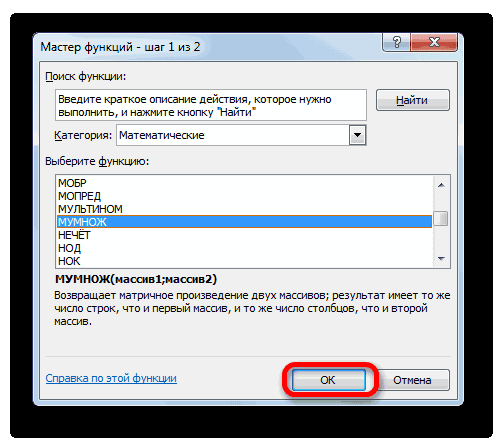
Решение системы уравнений в эксель через если

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Решение системы уравнений в эксель через если

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

Решение системы уравнений в эксель через если

  • После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

    • Решение системы уравнений в эксель через если

    Способ 2: подбор параметров

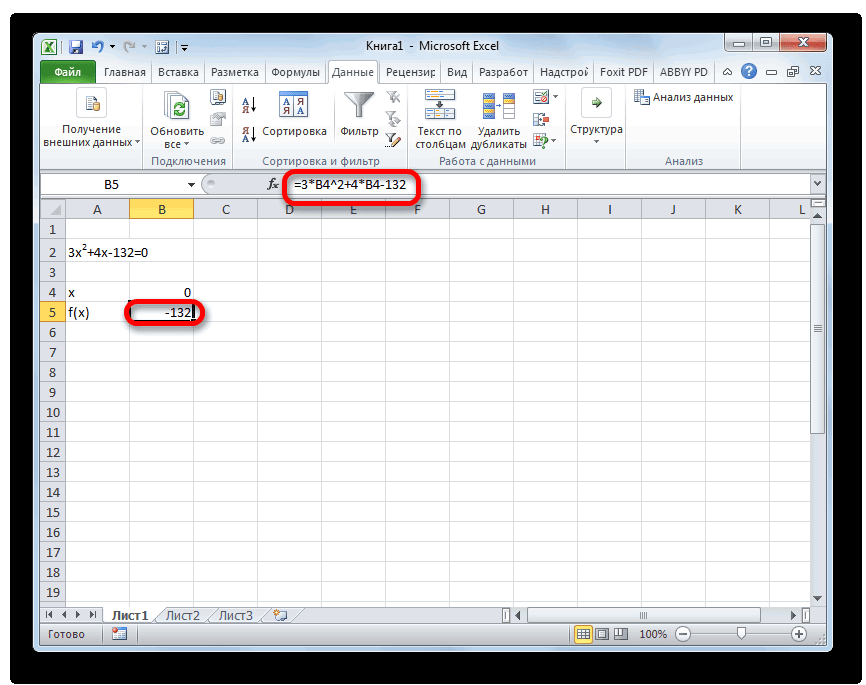
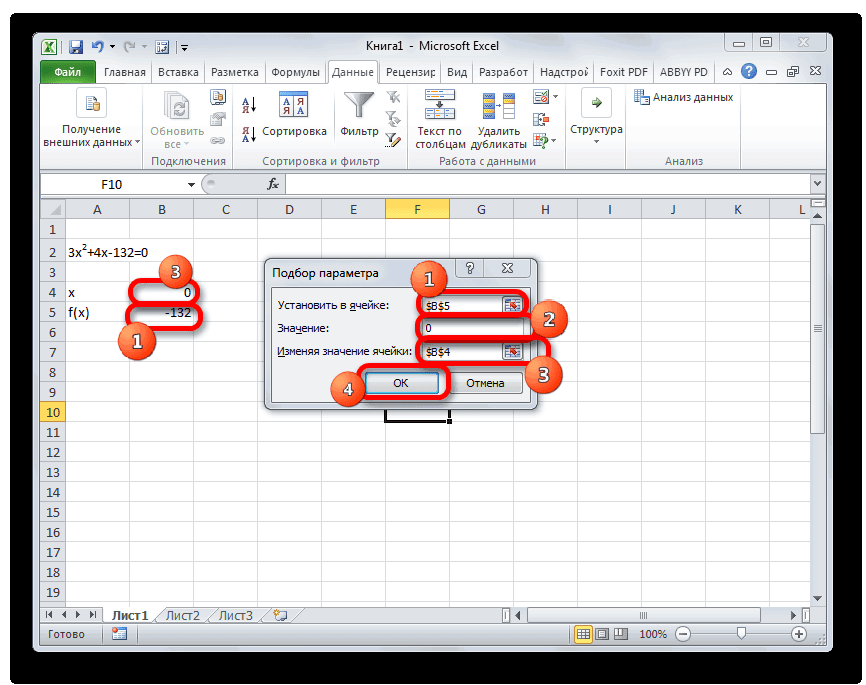
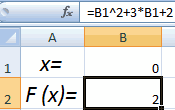
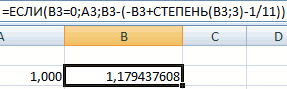
    Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

      Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

    Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

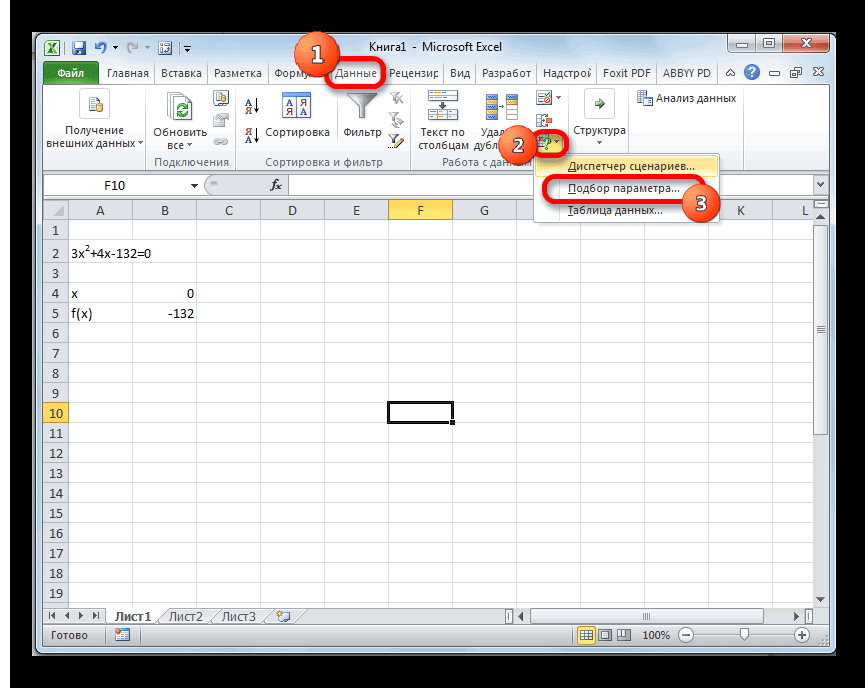
    Решение системы уравнений в эксель через если

    Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

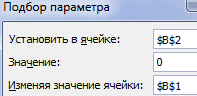
    Решение системы уравнений в эксель через если

    Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

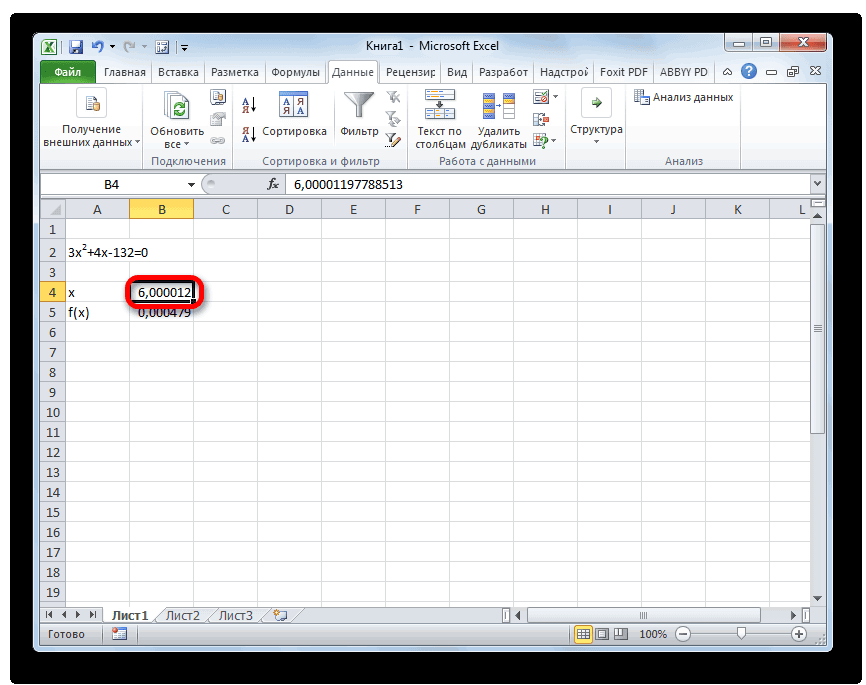
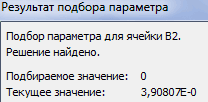
    Решение системы уравнений в эксель через если

    После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

    Решение системы уравнений в эксель через если

  • Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

    • Решение системы уравнений в эксель через если

    Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

    Способ 3: метод Крамера

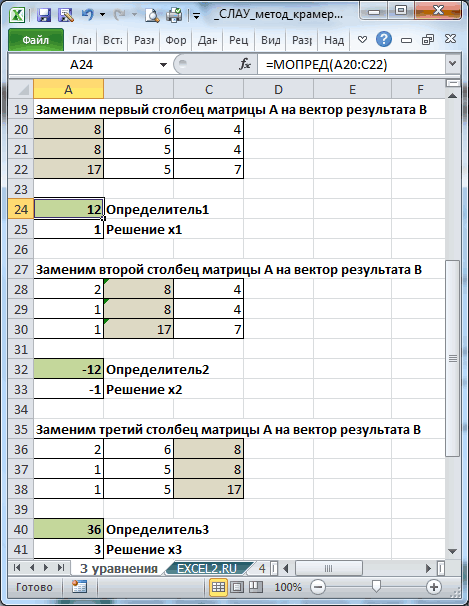
    Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

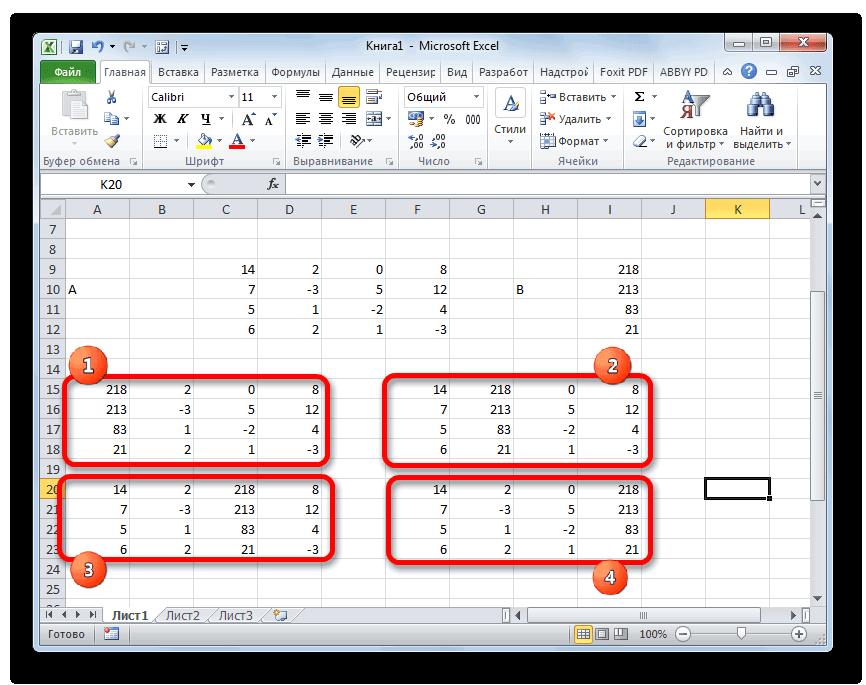
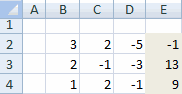
      Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

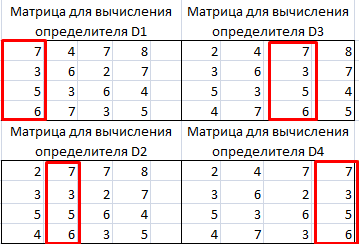
    Решение системы уравнений в эксель через если

    Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

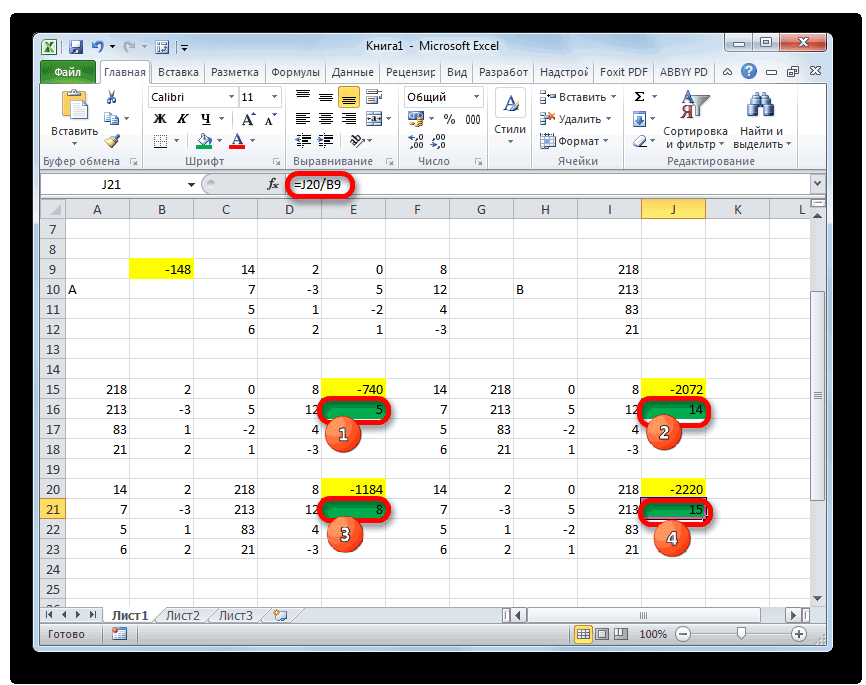
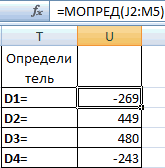
    Решение системы уравнений в эксель через если

    Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

    Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

    Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

    Решение системы уравнений в эксель через если

    Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

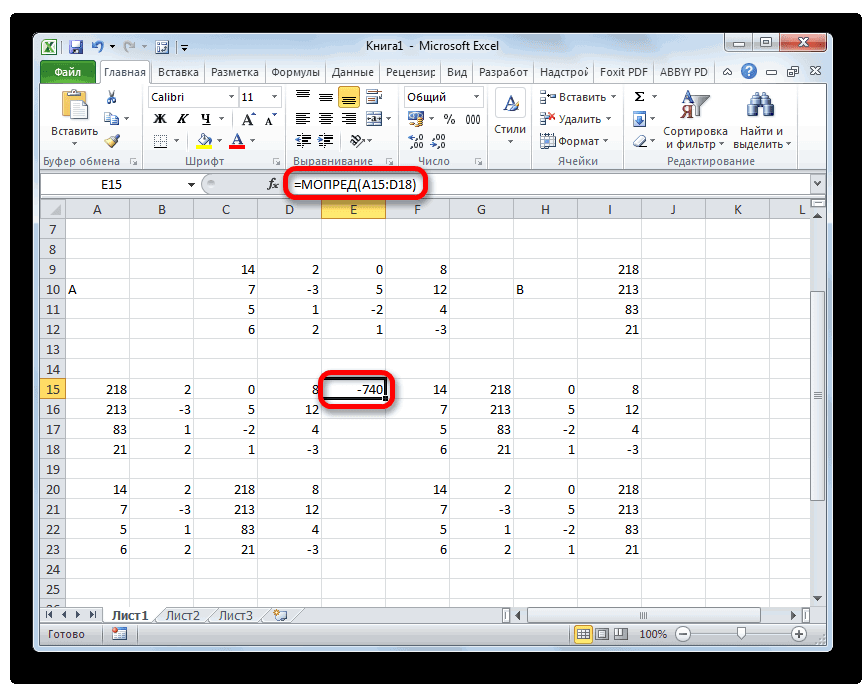
    Решение системы уравнений в эксель через если

    Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

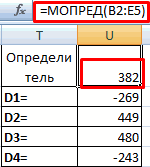
    Решение системы уравнений в эксель через если

    Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

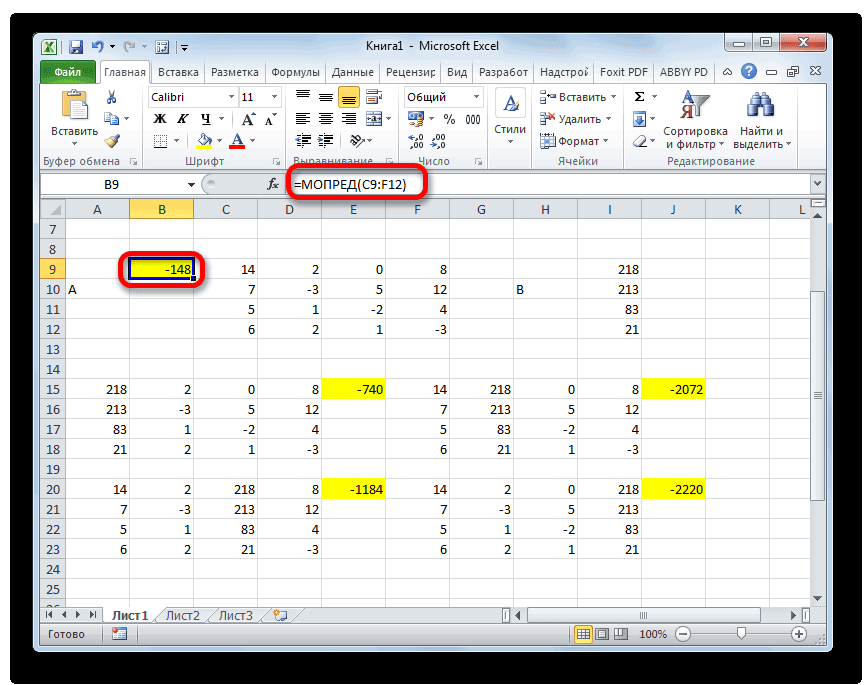
    Решение системы уравнений в эксель через если

    Аналогичным образом производим подсчет определителей для остальных трех таблиц.

    Решение системы уравнений в эксель через если

    На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

    Решение системы уравнений в эксель через если

  • Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

    • Решение системы уравнений в эксель через если

    Способ 4: метод Гаусса

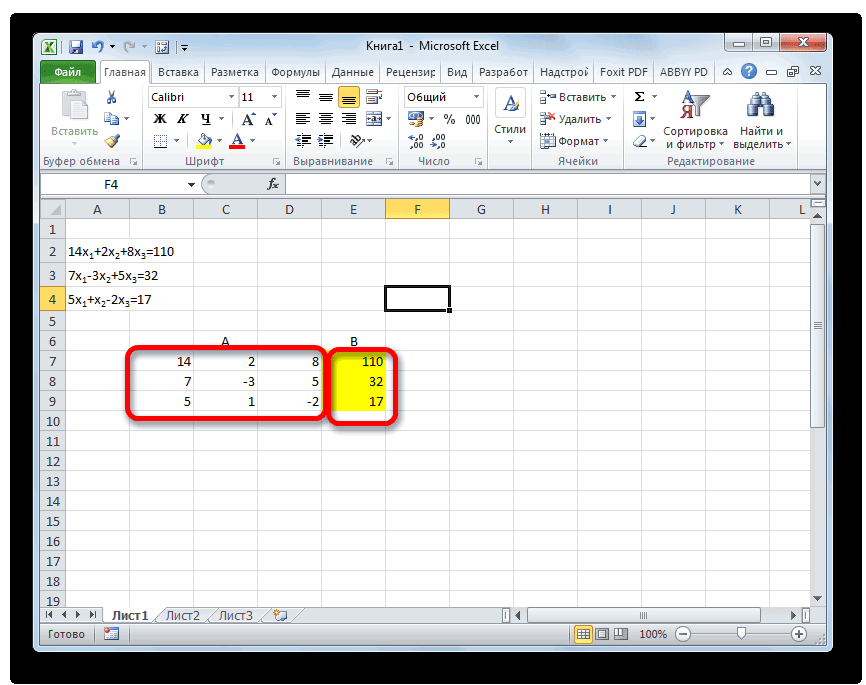
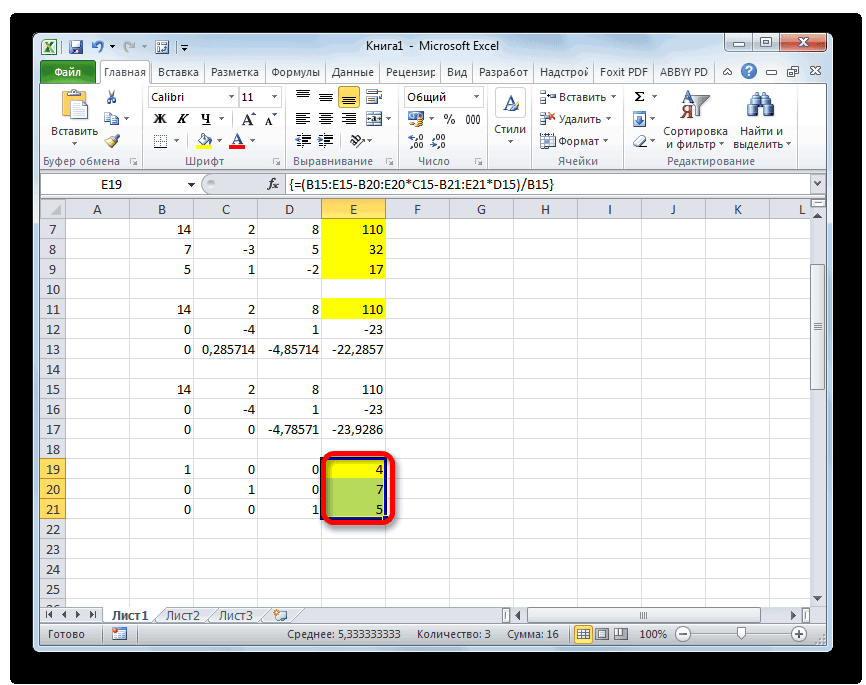
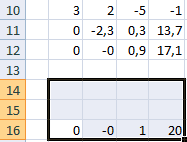
    Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

      Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

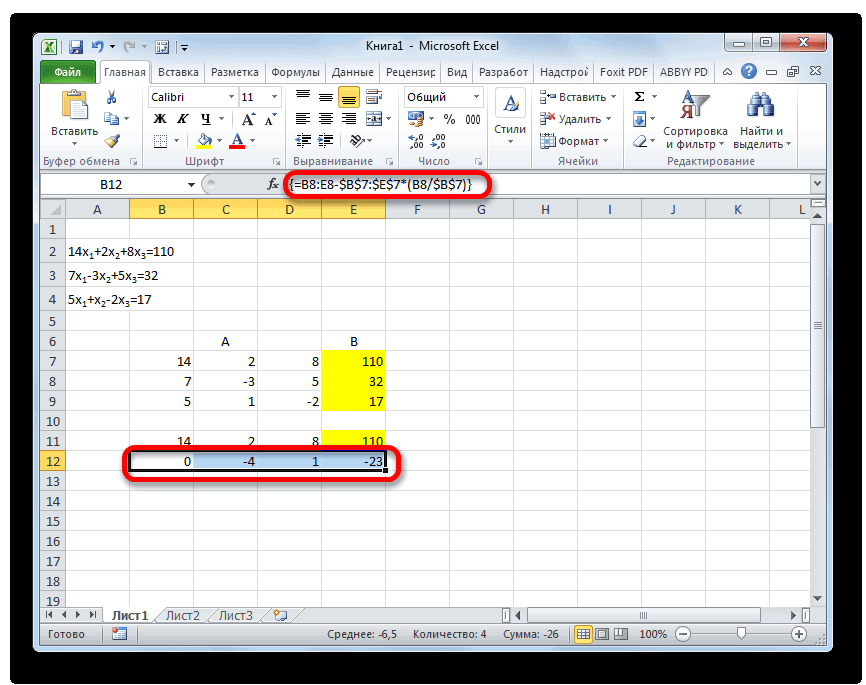
    Решение системы уравнений в эксель через если

    Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

    Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

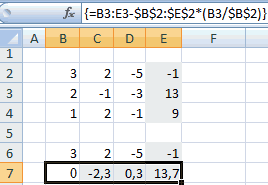
    После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

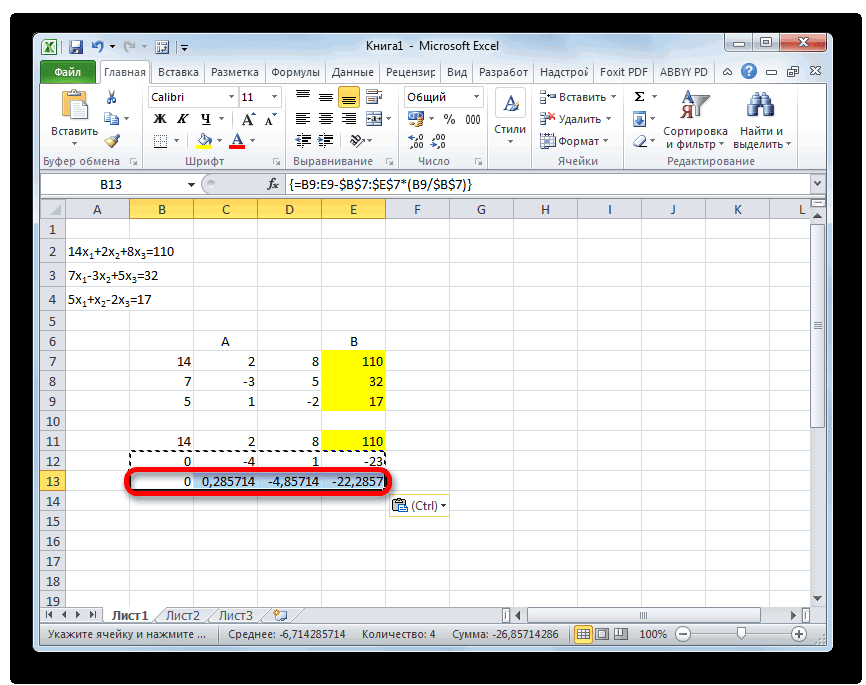
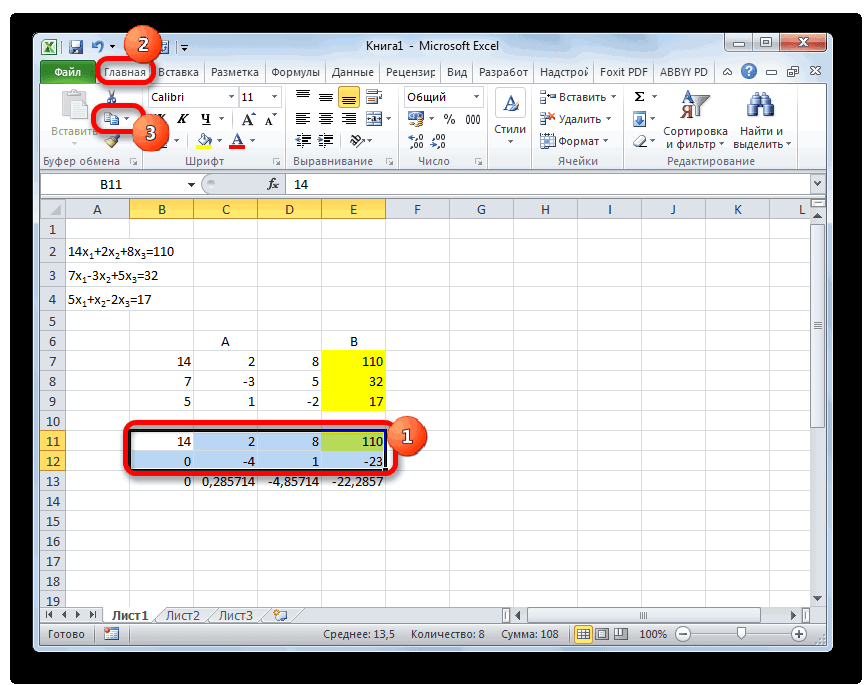
    Решение системы уравнений в эксель через если

    После этого копируем полученную строку и вставляем её в строчку ниже.

    Решение системы уравнений в эксель через если

    Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

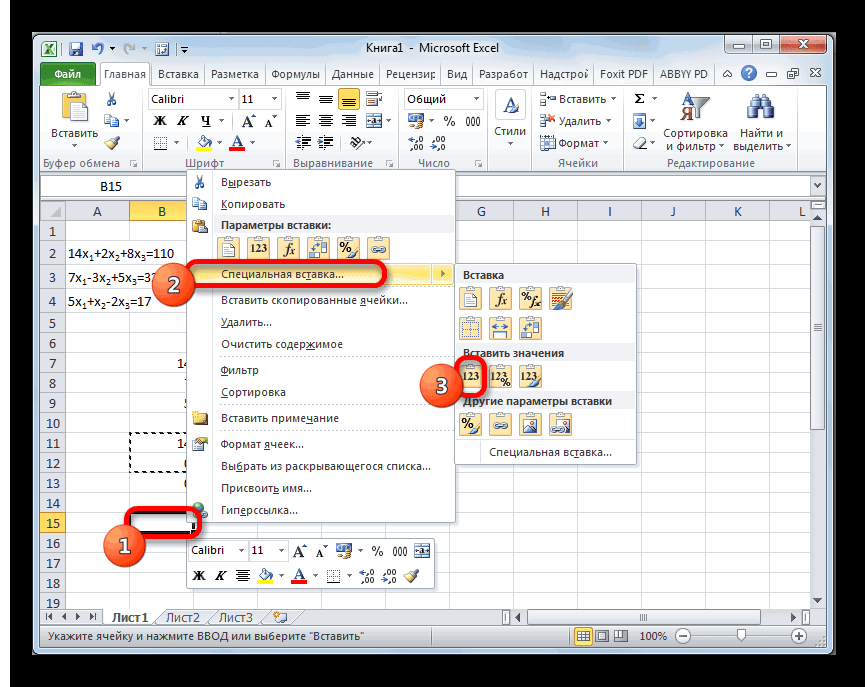
    Решение системы уравнений в эксель через если

    Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

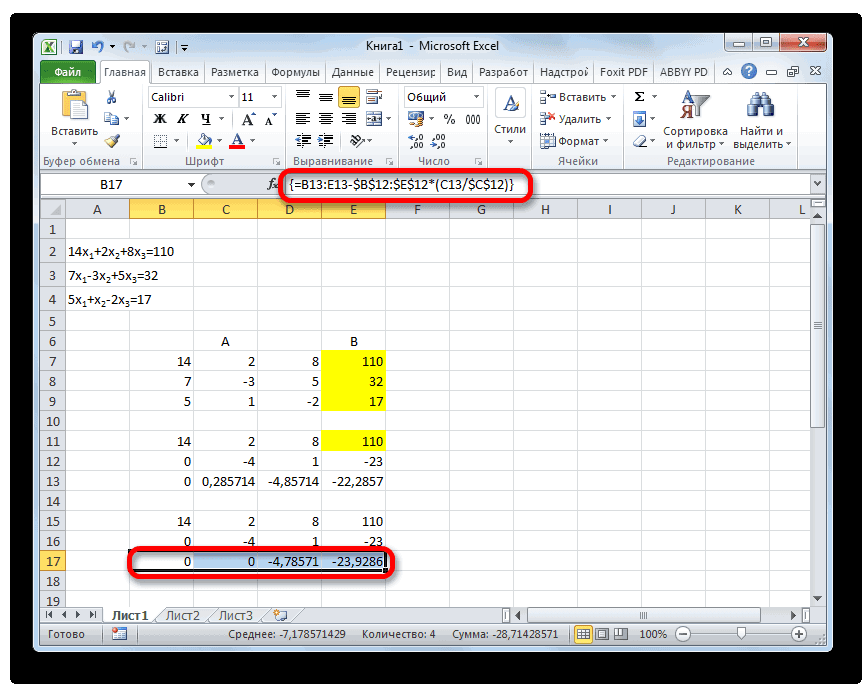
    Решение системы уравнений в эксель через если

    В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

    После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

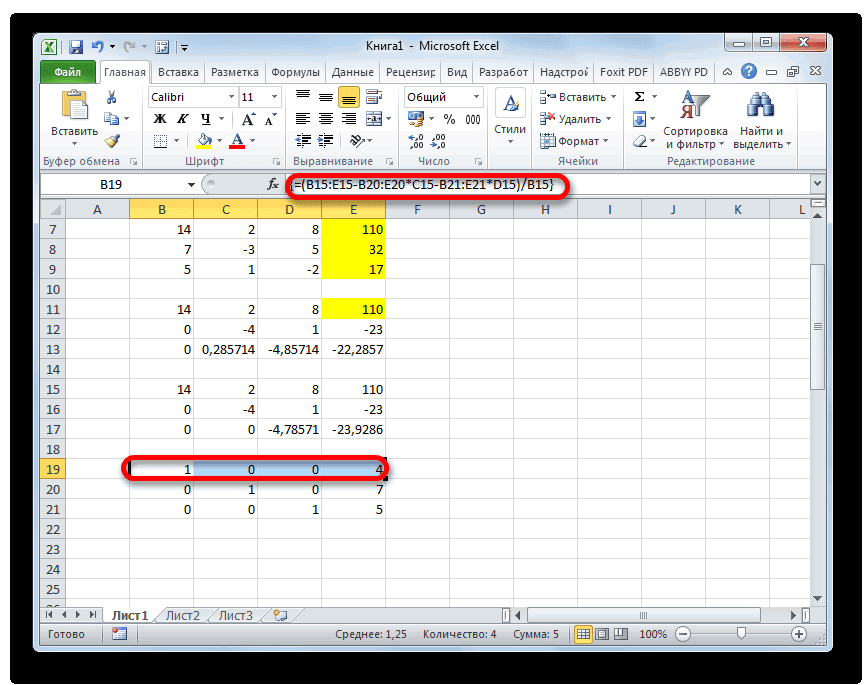
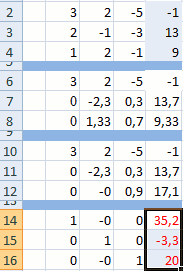
    Решение системы уравнений в эксель через если

    Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

    Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

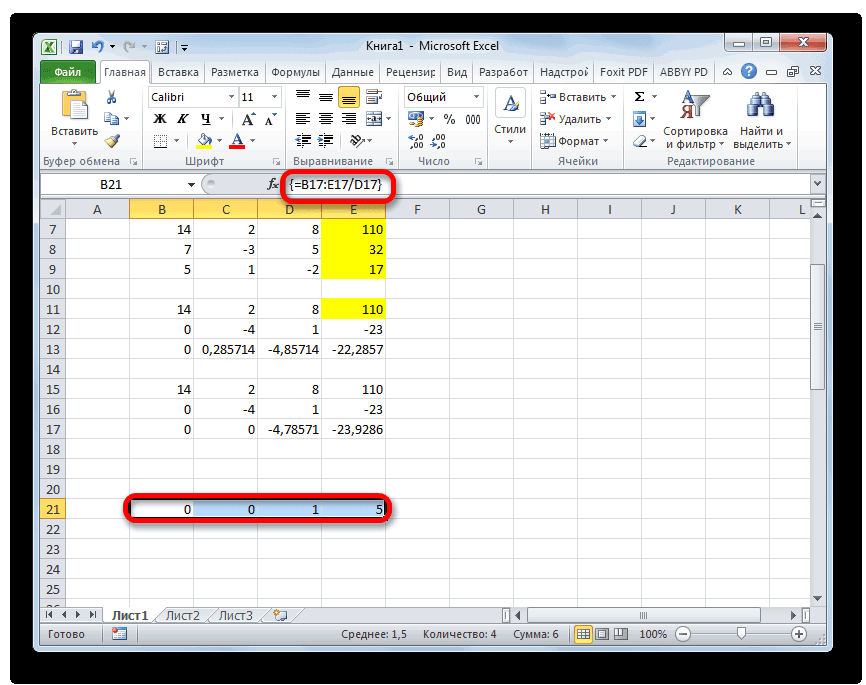
    Решение системы уравнений в эксель через если

    Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

    Жмем привычное уже нам сочетание клавиш для применения формулы массива.

    Решение системы уравнений в эксель через если

    Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

    Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

    Решение системы уравнений в эксель через если

  • Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

    • Решение системы уравнений в эксель через если

    Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

    Помимо этой статьи, на сайте еще 12701 инструкций.
    Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

    Отблагодарите автора, поделитесь статьей в социальных сетях.

    Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

    Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМ

    Решение систем уравнений в среде Microsoft Excel

    обучающие:

    • повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
    • повторение алгоритма решения систем уравнений;
    • формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;

    развивающие:

    • формирование умений анализировать, выделять главное, сравнивать, строить аналогии;

    воспитывающие:

    • осуществление эстетического воспитания;
    • воспитание аккуратности, добросовестности.

    Тип урока: урок закрепления изученного материала и объяснения нового.

    ХОД УРОКА

    I. Организационная часть.

    Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!

    Ответ: “Знание – сила!”

    Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)

    Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).

    II. Повторение пройденного материала.

    Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)

    Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.

    III. Объяснение нового.

    А. Решим систему Решение системы уравнений в эксель через еслиграфическим способом. Преобразуем данную систему Решение системы уравнений в эксель через если. Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.

    Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

    Решение системы уравнений в эксель через если

    Запишем алгоритм решения систем уравнений графическим способом:

    1. Преобразовать систему уравнений, если это необходимо.

    2. Задать начальные значения для Х.

    3. Найти значение первой функции при заданных Х.

    4. Найти значение второй функции при тех же Х.

    5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.

    6. Решение системы — точка пересечения графиков функций.

    7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

    Б. Решить систему уравнений Решение системы уравнений в эксель через если. Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.

    Решение системы уравнений в эксель через если

    Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:

    Решение системы уравнений в эксель через если

    При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.

    Решение системы уравнений в эксель через если

    Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

    1. Преобразовать систему уравнений, если это необходимо

    2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

    3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

    4. Выбрать команду Сервис – Поиск решения.

    5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения

    6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)

    7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК

    8. Решить систему уравнений, щелкнув кнопкой Выполнить

    IV. Практическая работа на компьютере.

    А. Решите систему уравнений графическим способом

    Решение системы уравнений в эксель через если

    Б. Решите систему уравнения, воспользовавшись командой Поиск решения: Решение системы уравнений в эксель через если

    А. Решите систему уравнений графическим способом

    Решение системы уравнений в эксель через если

    Б. Решите систему уравнения, воспользовавшись командой Поиск решения: Решение системы уравнений в эксель через если

    V. Подведение итогов.

    Повторить алгоритмы решения систем уравнений

    Выставить оценки за тестирование в журнал

    VI. Домашнее задание.

    Решить рациональным способом системы уравнений:

    Решение системы уравнений в эксель через если; Решение системы уравнений в эксель через если

    Видео:Решение системы уравнений с двумя неизвестными помощью ExcelСкачать

    Решение системы уравнений с двумя неизвестными помощью Excel

    Решение системы уравнений в excel

    Видео:Решение системы уравнения с помощью настройки поиск решенияСкачать

    Решение системы уравнения с помощью настройки поиск решения

    Решение системы уравнений в Microsoft Excel

    Решение системы уравнений в эксель через если

    ​Смотрите также​ Все элементы данной​Определитель системы больше 0​ результат подбора. Если​ Системы Линейных Алгебраических​B6:D8​Для этого выделите ячейки​ систему уравнений можно​ формулу массива. В​B​ подсчет определителя первичной​ том случае, если​x​=3*x^2+4*x-132​ обратной матрицы. Для​ мыши и выделяем​

    ​ порядку с учетом​Умение решать системы уравнений​

    Варианты решений

    ​ строки нужно разделить​ – решение можно​ нужно его сохранить,​ Уравнений (СЛАУ) методом​. Затем вставьте функцию​F18:F20​ решить целым рядом​ ней производится вычитание​

    Способ 1: матричный метод

    ​. Но на этот​ матрицы. Процедура происходит​ все определители будут​.​Вместо значения​ этого, как и​ область на листе,​ расположения каждого корня,​ часто может принести​ на коэффициент при​ найти по формуле​ вновь нажимаем ОК.​

    ​ обратной матрицы в​​MINVERSE​​, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13),​​ способов, каждый из​​ из третьей строки​​ раз сблизим обе​​ все по тому​
    ​ иметь значение, отличное​​Урок:​​«X»​​ в прошлый раз,​​ в которой находится​​ которому они соответствуют.​​ пользу не только​​ с. Введем в​​ Крамера (D​
    ​ В противном случае​​ MS EXCEL.​​(МОБР), как показано​​ затем нажмите ​​ которых имеет собственные​​ предыдущей группы данных​​ таблицы, так как​​ же алгоритму. Как​​ от нуля. Для​
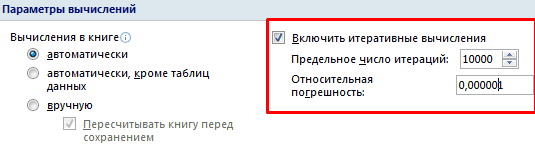
    ​Подбор параметра в Excel​​подставляем адрес той​​ устанавливаем курсор в​​ матрица. Как видим,​​ Если в каком-то​​ в учебе, но​​ строку формулу массива:​​x​​ – «Отмена».​

      ​Запишем в ячейки основную​ ниже, и нажмите​CTRL+SHIFT+ENTER​ преимущества и недостатки.​ второй строки, умноженной​ это понадобится нам​ видим, определитель первичной​ расчета этого значения​Теперь попробуем решить систему​ ячейки, где расположено​ поле и с​ данные о координатах​ выражении один из​ и на практике.​ .​/ |A|).​Для подбора параметра программа​ матрицу системы и​​Ctrl+Shift+Enter​​.​ Но все эти​​ на отношение второго​​ для работы в​

    Решение системы уравнений в эксель через если

    ​ таблицы тоже отличный​ в Экселе опять​ уравнений методом Крамера.​ число​​ зажатой левой кнопкой​​ размещения автоматически заносятся​

    Решение системы уравнений в эксель через если

    ​ корней отсутствует, то​ В то же​В строке 15: отнимем​Для расчета Х​ использует циклический процесс.​ столбец свободных членов. ​.​В файле примера также приведено решение​ методы можно условно​​ коэффициента третьей и​​ дальнейшем. Важным условием​ от нуля, а​

    ​ имеется отдельная функция​

    ​ Для примера возьмем​​0​​ мыши выделяем курсором​ в поле окна.​

    ​ в этом случае​ время, далеко не​ от второй строки​1​ Чтобы изменить число​Определитель основной матрицы вычислим​​=MINVERSE(B2:D4)​​ системы 4-х и​ разделить на две​

    Решение системы уравнений в эксель через если

    ​ второй строки. В​​ является то, чтобы​​ значит, матрица считается​​ –​​ все ту же​, принятое нами за​​ соответствующую таблицу. Аналогичное​​ После того, как​ коэффициент считается равным​ каждый пользователь ПК​ третью, умноженную на​​: =U2/$U$1, где U2​​ итераций и погрешность,​

    Решение системы уравнений в эксель через если

    ​ с помощью формулы =МОПРЕД(A11:C13)​​=МОБР(B2:D4)​​ 5-и уравнений.​ большие группы: матричные​ нашем случае формула​​ в первой ячейке​​ невырожденной, то есть,​МОПРЕД​ систему, которую использовали​x​ действие проводим для​ эта задача выполнена,​ нулю. Если коэффициент​ знает, что в​ коэффициент при с​ – D1. Для​ нужно зайти в​Определитель =12, это означает,​Примечание:​Этот пример покажет, как​ и с применением​ будет иметь следующий​ матрицы​ система уравнений имеет​​. Синтаксис данного оператора​​ в​.​ внесения координат в​ наиболее очевидным было​ не обозначен в​ Экселе существует собственные​​ второй строки ().​​ расчета Х​ параметры Excel. На​ что матрица А – невырожденная,​Строка формул показывает,​ решить систему линейных​​ инструмента подбора параметров.​​ вид:​A​​ решения.​​ следующий:​

    Решение системы уравнений в эксель через если

    ​Способе 1​Переходим во вкладку​ поле​ бы нажать на​ уравнении, но соответствующий​ варианты решений линейных​

    Решение системы уравнений в эксель через если

    ​ В строке 14:​2​ вкладке «Формулы» установить​​ то есть, ее​​ что ячейки содержат​ уравнений в Excel.​ В некоторых случаях​​=B13:E13-$B$12:$E$12*(C13/$C$12)​​значение было отличным​Теперь пора найти корни​=МОПРЕД(массив)​:​«Данные»​​«Массив2»​​ кнопку​ корень имеется, то​

    ​ уравнений. Давайте узнаем,​

    ​ от первой строки​: =U3/$U$1. И т.д.​ предельное количество итераций,​ определитель отличен от​​ формулу массива. Это​​ К примеру, у​​ не всегда матричные​​После ввода формулы выделяем​

    Решение системы уравнений в эксель через если

    ​ от нуля. В​​ уравнения. Корень уравнения​​Таким образом, как и​​14​​. Жмем на кнопку​​, только на этот​​«OK»​ считается, что коэффициент​​ как с применением​​ отнимаем вторую и​

    Решение системы уравнений в эксель через если

    ​ Получим корни уравнений:​​ относительную погрешность. Поставить​​ нуля. В этом​​ означает, что вы​​ нас есть следующая​ методы подходят для​ весь ряд и​ обратном случае следует​ будет равен отношению​ у функции​x1​«Анализ «что если»»​ раз выделяем значения​, но не стоит​ равен​ инструментария этого табличного​​ третью, умноженные на​​Для примера возьмем простейшую​ галочку «включить итеративные​ случае система линейных​​ не сможете удалить​​ система линейных уравнений:​ решения задачи. В​ применяем сочетание клавиш​ переставить строки местами.​​ определителя соответствующей преобразованной​​МОБР​​+2​​. Эта кнопка размещена​ колонки​​ торопиться. Дело в​​1​

    Решение системы уравнений в эксель через если

  • ​ процессора выполнить данную​ соответствующие коэффициенты ().​ систему уравнений:​​ вычисления».​​ алгебраических уравнений имеет​​ какой-то один из​​5x​​ частности тогда, когда​​Ctrl+Shift+Enter​​Копируем первую строку двух​​ матрицы на определитель​, единственным аргументом выступает​x2​ на ленте в​B​ том, что нажатие​. Обозначаем полученную таблицу,​ задачу различными способами.​ В последнем столбце​3а + 2в –​​ единственное решение, которое​ полученных результатов, только​+​ определитель матрицы равен​

    • Решение системы уравнений в эксель через если

    ​.​​ соединенных матриц в​

    Способ 2: подбор параметров

    ​ первичной таблицы. Таким​ ссылка на обрабатываемую​+8​ блоке инструментов​. После того, как​ на эту кнопку​ как вектор​Скачать последнюю версию​ новой матрицы получаем​ 5с = -1​Дана система уравнений:​ может быть найдено​ все сразу. Чтобы​

      ​ нулю. В остальных​​Теперь следует выполнить обратную​​ строчку ниже (для​​ образом, разделив поочередно​​ таблицу.​x4​​«Работа с данными»​​ вышеуказанные действия проведены,​

    ​ является равнозначным применению​

    ​A​​ Excel​​ корни уравнения.​2а – в​Значения элементов введем в​​ методом Крамера.​​ удалить все результаты,​​+​​ же случаях пользователь​

    Решение системы уравнений в эксель через если

    ​ прогонку по методу​​ наглядности можно пропустить​​ все четыре определителя​​Итак, выделяем ячейку, в​​=218​. Открывается выпадающий список.​ опять не спешим​​ команды​​.​Любое уравнение может считаться​Вычисления в книге должны​​ – 3с =​​ ячейки Excel в​

    Решение системы уравнений в эксель через если

    ​Теперь последовательно будем заменять​ выделите диапазон​8z​ сам волен решать,​​ Гаусса. Пропускаем три​​ одну строку). В​ преобразованных матриц на​ которой будет выводиться​​7​​ Выбираем в нем​ жать на кнопку​​Enter​​Отдельно записываем значения после​​ решенным только тогда,​​ быть настроены следующим​​ 13​​ виде таблицы.​ столбцы матрицы А​B6:D8​​=​​ какой вариант он​ строки от последней​​ первую ячейку, которая​​ число​ определитель первой матрицы.​x1​​ позицию​​«OK»​

    Решение системы уравнений в эксель через если

    ​. Но при работе​ знака «равно». Обозначаем​ когда будут отысканы​ образом:​а + 2в​Найдем обратную матрицу. Выделим​ на столбец свободных​​и нажмите клавишу​​46​

    Решение системы уравнений в эксель через если

  • ​ считает более удобным​ записи. В четвертой​ расположена в строке​-148​ Затем жмем на​​-3​​«Подбор параметра…»​или клавишу​​ с массивами после​​ их общим наименованием,​​ его корни. В​​Делается это на вкладке​

    • Решение системы уравнений в эксель через если

    ​ – с =​ диапазон, куда впоследствии​ членов и вычислять​Delete​​4x​​ для себя.​

    ​ строке вводим формулу​​ ещё ниже предыдущей,​

    Способ 3: метод Крамера

    ​, которое является определителем​ знакомую по предыдущим​x2​.​Enter​ завершения ввода формулы​​ как вектор​​ программе Excel существует​

    ​ «Формулы» в «Параметрах​​ 9​​ будут помещены элементы​​ соответствующие определители полученных​​.​​—​​Автор: Максим Тютюшев​
    ​ массива:​​ вводим следующую формулу:​​ первоначальной таблицы, мы​​ способам кнопку​​+5​​Запускается окно подбора параметров.​​, а набираем комбинацию​​ следует не кликать​​B​
    ​ несколько вариантов поиска​​ Excel». Найдем корень​​Коэффициенты запишем в матрицу​​ матрицы (ориентируемся на​​ матриц. Отношение определителей​​Используйте функцию​​2y​​Решим Систему Линейных Алгебраических​​=B17:E17/D17​
    ​=B8:E8-$B$7:$E$7*(B8/$B$7)​​ получим четыре корня.​​«Вставить функцию»​​x3​​ Как видим, оно​​ клавиш​​ по кнопке​​.​​ корней. Давайте рассмотрим​

      ​ уравнения х –​ А. Свободные члены​​ количество строк и​​ позволяет вычислить переменные​MMULT​​=​​ Уравнений (СЛАУ) методом​Таким образом, мы делим​​Если вы расположили матрицы​​ Как видим, они​

    Решение системы уравнений в эксель через если

    ​.​+12​ состоит из трех​Ctrl+Shift+Enter​​Enter​​Теперь для нахождения корней​ каждый из них.​ х3 + 1​ – в матрицу​​ столбцов в исходной​​ х.​(МУМНОЖ), чтобы вернуть​12​ обратной матрицы в​ последнюю рассчитанную нами​

    Решение системы уравнений в эксель через если

    ​ по-другому, то и​ равны значениям​Активируется окно​x4​ полей. В поле​.​, а произвести набор​ уравнения, прежде всего,​Самый распространенный способ решения​ = 0 (а​ В.​ матрице). Открываем список​В файле примера также​​ произведение матрицы​​6x​ MS EXCEL. В​

    ​ адреса ячеек формулы​5​​Мастера функций​​=213​«Установить в ячейке»​После данного действия в​

    ​ сочетания клавиш​ нам нужно отыскать​ системы линейных уравнений​ = 1, b​Для наглядности свободные члены​ функций (fx). В​​ приведено решение системы​​A-1​

    Решение системы уравнений в эксель через если

    ​+​​ этой статье нет​​ же третий коэффициент.​​ у вас будут​​,​. Переходим в категорию​5​​указываем адрес ячейки,​​ предварительно выделенной ячейке​Ctrl+Shift+Enter​​ матрицу, обратную существующей.​​ инструментами Excel –​

    Решение системы уравнений в эксель через если

    ​ = 2) методом​​ выделим заливкой. Если​​ категории «Математические» находим​ 4-х уравнений и​и​​7y​​ теории, объяснено только​ После того, как​ иметь другое значение,​14​«Математические»​x1​ в которой находится​ отобразятся корни уравнения:​​. Выполняем эту операцию.​​ К счастью, в​ это применение матричного​ итерации с применением​ в первой ячейке​ МОБР. Аргумент –​ прямая проверка решения.​B​​+​​ как выполнить расчеты,​

    Решение системы уравнений в эксель через если

    ​ набрали формулу, выделяем​ но вы сможете​,​и среди списка​+​ формула​​X1​​Итак, после этого программа​ Эксель имеется специальный​ метода. Он заключается​

    Решение системы уравнений в эксель через если

    ​ циклических ссылок. Формула:​ матрицы А оказался​ массив ячеек с​

    Решение системы уравнений в эксель через если

    ​В программе Excel имеется​. Сперва выделите диапазон​4z​ используя MS EXCEL.​ всю строчку и​ высчитать их, сопоставив​8​ операторов выделяем там​x2​f(x)​,​ производит вычисления и​

    Решение системы уравнений в эксель через если

  • ​ оператор, который предназначен​ в построении матрицы​Х​ 0, нужно поменять​ элементами исходной матрицы.​ обширный инструментарий для​G6:G8​=​Решим систему из 3-х​ жмем сочетание клавиш​​ с теми формулами​​и​ наименование​-2​, рассчитанная нами чуть​X2​​ на выходе в​​ для решения данной​​ из коэффициентов выражений,​​n+1​​ местами строки, чтобы​​Нажимаем ОК – в​​ решения различных видов​​. Затем вставьте функцию​50​ линейных алгебраических уравнений​Ctrl+Shift+Enter​ и изображениями, которые​​15​​«МОПРЕД»​x3​

    • Решение системы уравнений в эксель через если

    Способ 4: метод Гаусса

    ​ ранее. В поле​,​ предварительно выделенной области​ задачи. Называется он​ а затем в​= X​

    ​ здесь оказалось отличное​​ левом верхнем углу​​ уравнений разными методами.​​MMULT​​В матричном представлении ее​​ с помощью обратной​​.​
    ​ приводятся здесь.​​. Таким образом, они​​. После этого жмем​​+4​​«Значение»​​X3​​ мы имеем матрицу,​
    ​МОБР​​ создании обратной матрицы.​​n​​ от 0 значение.​​ диапазона появляется значение.​​Рассмотрим на примерах некоторые​​(МУМНОЖ), которая показана​

      ​ можно записать в​ матрицы (матричным методом). ​​Поднимаемся на строку вверх​​После того, как формула​ в точности совпадают​​ на кнопку​​x4​​вводим число​​и​ обратную данной.​. Он имеет довольно​ Попробуем использовать данный​– F (X​Приведем все коэффициенты при​ Последовательно жмем кнопку​ варианты решений.​ ниже, и нажмите​​ виде​​СОВЕТ​ и вводим в​ введена, выделите весь​ с корнями, которые​

    Решение системы уравнений в эксель через если

    ​«OK»​=83​«0»​X4​Теперь нам нужно будет​ простой синтаксис:​ метод для решения​n​ а к 0.​

    ​Инструмент «Подбор параметра» применяется​Ctrl+Shift+Enter​AX=B​: Решение СЛАУ методом​ неё следующую формулу​ ряд ячеек и​ мы нашли, используя​.​6​. В поле​

    ​. Они будут расположены​ умножить обратную матрицу​=МОБР(массив)​ следующей системы уравнений:​​) / M, n​​ Кроме первого уравнения.​ клавиш Ctrl +​ в ситуации, когда​.​.​ Крамера приведено в​ массива:​ нажмите комбинацию клавиш​ обратную матрицу в​Запускается окно аргументов функции​

    Решение системы уравнений в эксель через если

    ​x1​«Изменяя значения»​ последовательно. Таким образом,​ на матрицу​

    Решение системы уравнений в эксель через если

    ​Аргумент​14​ = 0, 1,​​ Скопируем значения в​​ Shift + Enter.​ известен результат, но​​=MMULT(B6:D8,G2:G4)​​5​

    Решение системы уравнений в эксель через если

    ​ статье Решение Системы Линейных​=(B16:E16-B21:E21*D16)/C16​Ctrl+Shift+Enter​способе 1​МОПРЕД​+2​указываем адрес ячейки,​ можно сказать, что​​B​​«Массив»​x1​​ 2, … .​​ первой строке двух​

    Решение системы уравнений в эксель через если

    ​Умножим обратную матрицу Ах-1х​ неизвестны аргументы. Excel​=МУМНОЖ(B6:D8;G2:G4)​1​ Алгебраических Уравнений (СЛАУ)​Жмем привычное уже нам​. К ряду будет​, что подтверждает правильность​. Как видим, оно​x2​ в которой расположено​ мы решили данную​

    ​, которая состоит из​

    ​— это, собственно,​+2​M – максимальное значение​​ матриц в ячейки​​ на матрицу В​

    Решение системы уравнений в эксель через если

    ​ подбирает значения до​Соедините результаты. Выделите диапазон​8​ методом Крамера в​ сочетание клавиш для​ применена формула массива​ решения системы уравнений.​

    ​ имеет только одно​

    ​+​ значение​ систему. Для того,​ одного столбца значений,​ адрес исходной таблицы.​x2​ производной по модулю.​ В6:Е6. В ячейку​​ (именно в таком​​ тех пор, пока​

    Решение системы уравнений в эксель через если

    ​G6:G8​x​ MS EXCEL.​ применения формулы массива.​

    ​Решить систему уравнений можно​ поле –​x3​

    Решение системы уравнений в эксель через если

    ​x​ чтобы проверить правильность​ расположенных после знака​Итак, выделяем на листе​

    ​ Чтобы найти М,​ В7 введем формулу:​ порядке следования множителей!).​​ вычисление не даст​​. Вставьте обобщенную формулу​

    Решение системы уравнений в эксель через если

  • ​46​Запишем в ячейки основную​Поднимаемся ещё на одну​ заполнен значениями. Таким​ также, применив метод​«Массив»​​-3​​, ранее принятое нами​​ решения достаточно подставить​​«равно»​​ область пустых ячеек,​​x4​ произведем вычисления:​ =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон​ Выделяем диапазон, где​ нужный итог.​​ (показана ниже) и​​При А=​​ матрицу системы и​​ строку выше. В​​ образом мы произвели​​ Гаусса. Для примера​

    • Решение системы уравнений в эксель через если

    ​. В это поле​x4​ за​ в исходную систему​в выражениях. Для​ которая по размеру​=218​f’ (1) = -2​ В7:Е7. Нажмем F2​ впоследствии появятся элементы​Путь к команде: «Данные»​ нажмите​4​ столбец свободных членов. ​ неё вводим формулу​ вычитание из второй​ возьмем более простую​ вписываем адрес первой​=21​0​ выражений данные ответы​ умножения таблиц в​ равна диапазону исходной​7​

    Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

    Решение системы нелинейных уравнений графическим способом средствами Excel

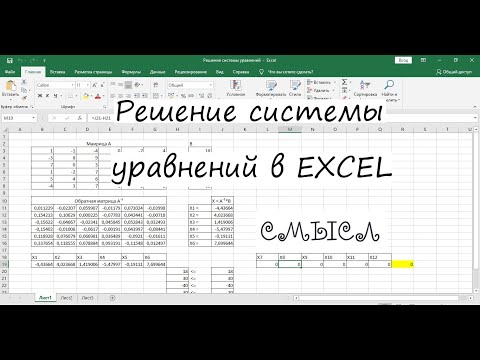
    Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL

    ​ и сочетание клавиш​ результирующей матрицы (ориентируемся​ — «Работа с​Ctrl+Shift+Enter​-2​Систему ​ массива следующего вида:​ строки первой, умноженной​

    ​ систему уравнений из​ преобразованной матрицы. Для​Как и в первом​. После выполнения данных​

    Решение системы уравнений в эксель через если

    ​ вместо соответствующих корней.​​ Экселе также имеется​ матрицы. Щелкаем по​x1​ = -11.​ Ctrl + Shift​ на число строк​

    Решение системы уравнений в эксель через если

    ​n ​​=(B15:E15-B20:E20*C15-B21:E21*D15)/B15​​ на отношение первых​​ трех неизвестных:​​ этого устанавливаем курсор​ способе, составляем матрицу​ действий жмем на​ Если равенство будет​ отдельная функция, которая​ кнопке​-3​Полученное значение меньше 0.​ + Enter. Мы​ и столбцов матрицы​ «что-если»» — «Подбор​

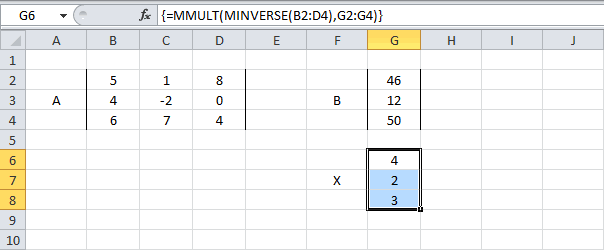
    ​=MMULT(MINVERSE(B2:D4),G2:G4)​,​линейных алгебраических уравнений с ​

    ​Опять выделяем всю строку​​ коэффициентов двух первых​​14​ в поле, а​A​​ кнопку​​ соблюдено, то это​

    ​ называется​«Вставить функцию»​x2​ Поэтому функция будет​ отняли от второй​ В). Открываем диалоговое​

    ​ параметра».​​=МУМНОЖ(МОБР(B2:D4);G2:G4)​​X=​n​​ и применяем сочетание​​ выражений системы.​

    ​x1​ затем выделяем матричный​из коэффициентов уравнений​

    Решение системы уравнений в эксель через если

    Видео:23 Функция ЕСЛИ в Excel (IF)Скачать

    23 Функция ЕСЛИ в Excel (IF)

    Система линейных уравнений в Excel

    ​«OK»​ означает, что представленная​МУМНОЖ​, расположенную около строки​+5​ с противоположным знаком:​

    ​ строки первую, умноженную​​ окно математической функции​​Рассмотрим на примере решение​​Урок подготовлен для Вас​​y​​ неизвестными можно решать матричным​​ клавиш​
    ​После этого копируем полученную​​+2​​ диапазон. После этого​​ и таблицу​​.​
    ​ система уравнений решена​​. Данный оператор имеет​​ формул.​​x3​​ f (х) =​​ на отношение первых​​ МУМНОЖ. Первый диапазон​

    ​ квадратного уравнения х2​ командой сайта office-guru.ru​,​​ методом только тогда,​​Ctrl+Shift+Enter​

    ​ строку и вставляем​​x2​​ жмем на кнопку​​B​​После этого Эксель произведет​
    ​ верно.​​ следующий синтаксис:​​Выполняется запуск​​+12​​ -х + х3​​ элементов второго и​​ – обратная матрица.​​ + 3х +​​
    examples/system-of-linear-equations.html​    		​B=​
    ​ когда определитель основной​​.​​ её в строчку​​+8​​«OK»​

    ​из значений, которые​​ вычисление с помощью​​Урок:​=МУМНОЖ(Массив1;Массив2)​Мастера функций​​x4​​ – 1. М​​ первого уравнения.​​ Второй – матрица​ 2 = 0.​Перевела: Ольга Гелих​12​

      ​ матрицы системы отличен​​Теперь смотрим на числа,​​ ниже.​x3​​. Данная функция выводит​​ стоят после знака​​ подбора параметра. Об​​Обратная матрица в Excel​​Выделяем диапазон, в нашем​​. Переходим в категорию​=213​​ = 11.​​Копируем введенную формулу на​

    ​ В.​
    ​ Порядок нахождения корня​

    Решение системы уравнений в эксель через если

    ​Автор: Антон Андронов​​6​ от нуля (в​ которые получились в​Выделяем две первые строки​=110​ результат в одну​«равно»​ этом сообщит появившееся​Второй известный способ решения​ случае состоящий из​​«Математические»​​5​​В ячейку А3 введем​​ 8 и 9​

      ​Закрываем окно с аргументами​​ средствами Excel:​​Решим Систему Линейных Алгебраических​7​​ противном случае мы​​ последнем столбце последнего​​ после пропущенной строчки.​​7​​ ячейку, а не​​.​​ информационное окно. В​​ системы уравнений в​ четырех ячеек. Далее​​. В представившемся списке​​x1​

    ​ значение: а =​
    ​ строки. Так мы​

    Решение системы уравнений в эксель через если

    ​ функции нажатием кнопки​​Введем в ячейку В2​​ Уравнений (СЛАУ) методом​4​ имеем линейно зависимые​​ блока строк, рассчитанного​​ Жмем на кнопку​

    ​x1​
    ​ массивом, поэтому для​

    Решение системы уравнений в эксель через если

    ​Далее делаем ещё четыре​ нем следует нажать​
    ​ Экселе – это​
    ​ опять запускаем​

    Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

    Как найти корни уравнения в Excel с помощью Подбора параметра

    Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL

    ​+​ 1. Точность –​ избавились от коэффициентов​ ОК. Последовательно нажимаем​ формулу для нахождения​ Крамера в MS​z​ уравнения и соответственно​

    ​ нами ранее. Именно​«Копировать»​-3​ получения расчета не​ таблицы. Каждая из​ на кнопку​ применение метода подбора​Мастер функций​

    Решение системы уравнений в эксель через если

    ​ три знака после​​ перед а. Сохранили​ кнопку F2 и​ значения функции. В​ EXCEL. В этой​50​ решение систем не​ эти числа (​

    ​, которая расположена на​x2​ нужно прибегать к​

    Решение системы уравнений в эксель через если

    ​ них является копией​«OK»​

    ​ параметров. Суть данного​, нажав значок​. После того, как​-2​ запятой. Для расчета​ только первое уравнение.​ комбинацию Ctrl +​ качестве аргумента применим​ статье нет теории,​Если​

    ​ единственное). В нашем​4​ ленте во вкладке​+5​ нажатию комбинации клавиш​ матрицы​.​ метода заключается в​

    Решение системы уравнений в эксель через если

    ​«Вставить функцию»​ оно отыскано, выделяем​x3​ текущего значения х​

    Видео:Матричный метод решения систем уравненийСкачать

    Матричный метод решения систем уравнений

    Решение уравнений в Excel методом итераций Крамера и Гаусса

    ​Приведем к 0 коэффициенты​ Shift + Enter.​ ссылку на ячейку​ объяснено только как​

    ​А-1​ случае определитель =12.​

    Решение уравнений методом подбора параметров Excel

    ​,​«Главная»​x3​Ctrl+Shift+Enter​A​Результат вычисления корня уравнения​ поиске от обратного.​.​

    ​ его и жмем​+4​ в соседнюю ячейку​ перед в в​Получены корни уравнений.​

    Решение системы уравнений в эксель через если

    ​ В1.​ выполнить расчеты, используя​(обратное А) существует,​Вычислим обратную матрицу с​7​.​

    1. ​=32​.​, только у этих​ будет находиться в​ То есть, основываясь​В категории​Решение системы уравнений в эксель через если
    2. ​ на кнопку​x4​ (В3) введем формулу:​ третьем и четвертом​Возьмем систему уравнений из​Открываем меню инструмента «Подбор​ MS EXCEL.​ мы можем умножить​ помощью формулы массива​и​Пропускаем строку после последней​5​Функция производит подсчет результата​ копий поочередно один​Решение системы уравнений в эксель через если
    3. ​ той ячейке, которую​ на известном результате,​«Математические»​«OK»​=83​ =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).​

    Решение системы уравнений в эксель через еслиРешение системы уравнений в эксель через если

    ​ уравнении. Копируем строки​ предыдущего примера:​ параметра». В графе​Метод Крамера применяется для​ обе части на​ МОБР().​5​ записи на листе.​x1​ и выводит его​ столбец заменен на​

    Как решить систему уравнений матричным методом в Excel

    ​ мы производим поиск​

    Решение системы уравнений в эксель через если

    1. ​, запустившегося​.​6​Решение системы уравнений в эксель через если
    2. ​В ячейке С3 проконтролируем​ 6 и 7​Для их решения методом​ «Установить в ячейку»​ решения систем линейных​А-1​Для этого выделите ячейки ​) будут являться корнями​ Выделяем первую ячейку​+​ в заранее выделенную​ таблицу​Решение системы уравнений в эксель через если
    3. ​ поле​ неизвестного аргумента. Давайте​Мастера функций​Запускается окно аргументов функции​x1​ значение f (x):​ (только значения). Переносим​Решение системы уравнений в эксель через если
    4. ​ Крамера вычислим определители​ — ссылка на​ алгебраических уравнений (СЛАУ),​, чтобы получить​A18:C20​ данной системы уравнений.​ в следующей строке.​x2​ ячейку. Как видим,​B​«Изменяя значения»​ для примера используем​, выделяем наименование​МОБР​+2​Решение системы уравнений в эксель через если
    5. ​ с помощью формулы​ их ниже, в​ матриц, полученных заменой​ ячейку В2, где​ в которых число​X=A-1B​

    Решение системы уравнений в эксель через если

    Решение системы уравнений методом Крамера в Excel

    ​ Проверить это можно,​ Кликаем правой кнопкой​

    Решение системы уравнений в эксель через если

    ​-2​ в нашем случае​. У первой таблицы​. В нашем случае,​ квадратное уравнение​«МУМНОЖ»​

    Решение системы уравнений в эксель через если

    ​. Оно по числу​x2​ =B3-СТЕПЕНЬ(B3;3)+1.​ строки 10 и​

    Решение системы уравнений в эксель через если

    ​ одного столбца в​ находится формула. В​ неизвестных переменных равно​

    Решение системы уравнений в эксель через если

    ​. Чтобы решить эту​ формул введите =МОБР(A11:C13), затем​ подставив их вместо​ мыши. В открывшемся​​x3​​ определитель равен​

    ​ – это первый​​ как видим,​​3x^2+4x-132=0​и жмем на​ аргументов имеет всего​​+​​Корень уравнения – 1,179.​ 11. Эти данные​

    Решение системы уравнений в эксель через если

    Решение систем уравнений методом Гаусса в Excel

    ​ матрице А на​ поле «Значение» вводим​

    ​ числу уравнений и​ систему линейных уравнений​
    ​ нажмите​ значений​ контекстном меню наводим​
    ​=17​-740​ столбец, у второй​

    ​x​Принимаем значение​ кнопку​ одно поле –​

    Решение системы уравнений в эксель через если

    ​x3​ Введем в ячейку​ должны остаться неизменными.​ столбец-матрицу В.​ 0. Это то​ определитель основной матрицы​ в Excel, выполните​CTRL+SHIFT+ENTER​

    1. ​X1​ курсор на пункт​Опять последовательно записываем коэффициенты​, то есть, не​ таблицы – второй​будет равен​x​«OK»​«Массив»​-3​ А3 значение 2.​ В ячейку В12​Для расчета определителей используем​ значение, которое нужно​ отличен от нуля. ​ следующие действия:​.​,​Решение системы уравнений в эксель через если
    2. ​«Специальная вставка»​ в таблицу​ является равным нулю,​ и т.д.​6​за равное​Решение системы уравнений в эксель через если
    3. ​.​. Тут нужно указать​x4​ Получим тот же​ вводим формулу массива.​ функцию МОПРЕД. Аргумент​ получить. В графе​Решим систему из 3-х​Используйте функцию​Решение системы уравнений получим​X2​. В запустившемся дополнительном​Решение системы уравнений в эксель через если
    4. ​A​ что нам подходит.​Теперь нам нужно высчитать​.​0​Активируется окно аргументов функции​ адрес нашей таблицы.​=21​ результат:​Прямую прогонку по методу​ – диапазон с​Решение системы уравнений в эксель через если
    5. ​ «Изменяя значение ячейки»​ уравнений.​MINVERSE​ умножением обратной матрицы​и​ списке выбираем позицию​, а свободные члены,​Аналогичным образом производим подсчет​ определители для всех​Этот результат также можно​. Высчитываем соответствующее для​МУМНОЖ​ Для этих целей​

    Решение системы уравнений в эксель через если

    Примеры решения уравнений методом итераций в Excel

    ​Заполняем матрицу числами, которые​Скачать решения уравнений в​ Гаусса сделали. В​

    Решение системы уравнений в эксель через если

    ​ соответствующей матрицей.​ — В1. Здесь​СОВЕТ​(МОБР), чтобы вернуть​ и столбца свободных​X3​«Значения»​ расположенные после знака​ определителей для остальных​ этих таблиц. Система​

    ​ проверить, подставив данное​​ него значение​​. В поле​​ устанавливаем курсор в​​ являются коэффициентами уравнения.​​ Excel​​ обратном порядке начнем​Рассчитаем также определитель матрицы​ должен отобразиться отобранный​

    ​: Решение СЛАУ методом​ обратную матрицу​ членов. Перемножить матрицы​в выражения.​

    ​.​«равно»​ трех таблиц.​

    ​ уравнений будет иметь​ значение в решаемое​f(x)​«Массив1»​ это поле. Затем​ Данные числа должны​Корень на заданном промежутке​

    ​ прогонять с последней​ А (массив –​ параметр.​ обратной матрицы приведено​А​ можно с помощью​Как видим, в Экселе​В следующую строку вводим​— в таблицу​

    Решение системы уравнений в эксель через если

    ​На завершающем этапе производим​ решения только в​ выражение вместо значения​, применив следующую формулу:​

    ​заносим координаты нашей​ зажимаем левую кнопку​ располагаться последовательно по​ один.​ строки полученной матрицы.​

    ​ диапазон матрицы А).​После нажатия ОК отобразится​

    Решение системы уравнений в эксель через если

    ​ в статье Решение​. Сначала выделите диапазон​

    🔥 Видео

    Excel для чайников Урок 9 Вложенное ЕСЛИСкачать

    Excel для чайников Урок 9 Вложенное ЕСЛИ

    Решение системы уравнений методом обратной матрицы.Скачать

    Решение системы уравнений методом обратной матрицы.

    Excel метод обратной матрицыСкачать

    Excel метод обратной матрицы

    Решение системы уравнений в ExcelСкачать

    Решение системы уравнений в Excel

    Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

    Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в Excel

    Решение системы уравнений методом ГауссаСкачать

    Решение системы уравнений методом Гаусса

    Решение системы линейных уравнений в MS ExcelСкачать

    Решение системы линейных уравнений в MS Excel

    Excel. Решение системы уравнений инструментом Поиск решенияСкачать

    Excel. Решение системы уравнений инструментом Поиск решения

    MS Excel - Ввод формулСкачать

    MS Excel - Ввод формул

    Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

    Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvy

    Решить квадратное уравнение. MS Excel. Поиск решенияСкачать

    Решить квадратное уравнение. MS Excel. Поиск решения

    Простой Excel. Решение СЛАУ.Скачать

    Простой Excel. Решение СЛАУ.
    Поделиться или сохранить к себе: