Решение системы уравнений с пятью неизвестными (3 видео)

Решение систем линейных уравнений

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).

Содержание

Метод Гаусса онлайн
Предупреждение
Метод Гаусса
Примеры решения системы линейных уравнений методом Гаусса
Решение системы M линейных уравнений с N неизвестными (СЛУ) методом Гаусса — OnLine Калкулятор
🔍 Видео

Видео:Решение системы уравнений методом ГауссаСкачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Система с тремя переменнымиСкачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

перемена местами двух уравнений в системе,
умножение какого-либо уравнения в системе на ненулевое действительное число,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

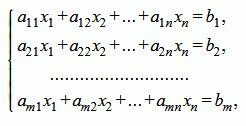Решение системы уравнений с пятью неизвестными

(1)

Запишем систему (1) в матричном виде:

Ax=b

(2)

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

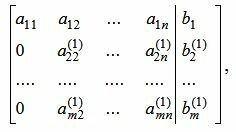(5)

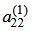
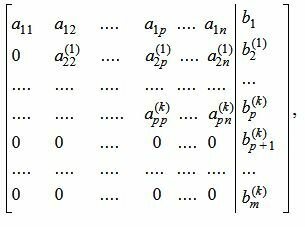На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 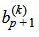. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

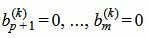
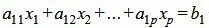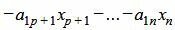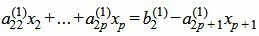Пусть . Тогда

(7)

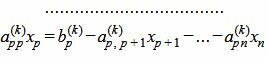Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

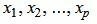
Видео:Решение системы уравнений с тремя переменнымиСкачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

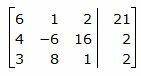Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

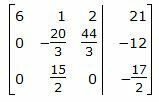Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

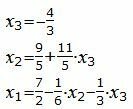Подставив верхние выражения в нижние, получим решение.

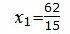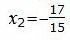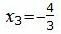Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

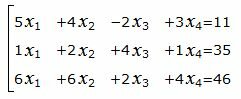Матричный вид записи: Ax=b, где

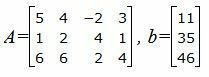Для решения системы, построим расширенную матрицу:

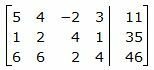Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

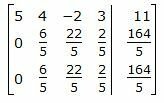Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

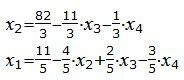где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

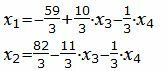где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

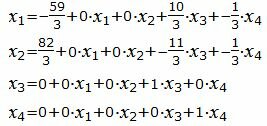Тогда векторное решение можно представить так:

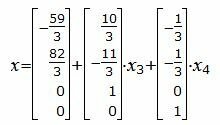где x₃, x₄− произвольные действительные числа.

Видео:Решение системы уравнений методом Крамера.Скачать

Решение системы M линейных уравнений с N неизвестными (СЛУ) методом Гаусса — OnLine Калкулятор

Система уравнений (СЛУ) будет решена методом Гаусса, прямо на сайте, с выводом всех промежуточных результатов и комментариями, вам необходимо только заполнить предлагаемые формы и нажать кнопку [Дальше—>]. Процесс вычисления будет представлен максимально подробно. Если вы используете наш сервис в первый раз, рекомендуем ознакомиться с правилами записи чисел в поля формы.

Смотри также :	подробности о сервисе.
Решение системы линейных уравнений метод Крамера (определителей).
Решение СЛУ матричный метод (обратной матрицы).

Для решения системы укажите ее параметры и способ представления чисел.