Решение системы уравнений с комплексными числами в маткаде (7 видео)

Решение системы уравнений с комплексными числами в маткаде

Глава 3. Работа с векторами и матрицами

3 . 12 Работа с комплексными числами

MathCAD с одинаковым успехом вычисляет выражения с действительными и комплексными числами.

Комплексные числа можно записывать в любой принятой в математике форме:

– обычной (в виде суммы действительной и мнимой частей числа) – с=а+ b · i ;

– в тригонометрической форме – c = A ·( sin ( φ )+ i · cos (φ));

– в экспоненциальной форме – c = A · e i ·φ .

Для ввода мнимой единицы надо набрать с клавиатуры 1 i или 1 j и ввести число. При выведении курсора из области числа символ 1 исчезает, остается комплексное число в привычном виде (рис. 3.23 ).

расчет токов в цепи по уравнениям Кирхгофа ORIGIN:=1

Рис. 3. 23 Ввод комплексных чисел

В качестве примера рассмотрим расчет токов и напряжений в цепи переменного тока по законам Кирхгофа. В этом случае ЭДС в цепи Е, напряжение U , токи J , сопротивление Z – комплексные числа. ЭДС Е задана в экспоненциальной форме, но при нажатии клавиши=выводится в обычном виде. После ввода констант в комплексной форме все формулы записываются также, как и для действительных чисел. При расчете вектора напряжений на различных участках цепи по закону Ома использован оператор векторизации для расчета попарных произведений (рис. 3.24 ).

Расчет напряжений по закону Ома

без оператора векторизации выведено скалярное произведение векторов

это не аргумент функции—без вывод комплексно-сопряженных чисел

оператора векторизации не обойтись

Рис. 3. 24 Расчеты с векторами комплексных чисел

В MathCAD есть оператор преобразования комплексного числа в комплексно – сопряженное. Он не представлен на математической панели, а вызывается с помощью символа “ .

Модуль комплексного числа вычисляется оператором || вводимым с панелей Calculator (Калькулятор) или Matrix (Матрица). Тот же оператор позволяет вычислить модуль вектора или определитель матрицы.

Аргумент комплексного числа вычисляется по формуле встроенной функцией arg ( A ), которая выдает угол поворота вектора в системе координат Re – Im (рис. 3.25 ).

модуль комплексного числа. необходим оператор векторизации

аргумент комплексного числа

угол в радианах угол в градусах

Рис. 3. 25 Вычисление модуля и аргумента комплексных чисел

Содержание

Решение систем уравнений в MathCad
Использование метода Given — Find:
Использование метода Solve:
MathCAD — это просто! Часть 19. Немного о работе с комплексными числами
📽️ Видео

Видео:Комплексные числа в MathCAD 14 (24/34)Скачать

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Видео:Приближенное решение систем уравнений в MathCAD 14 (30/34)Скачать

Использование метода Given — Find:

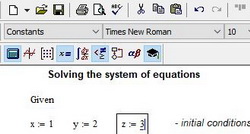
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

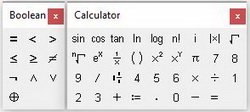
Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

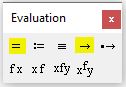
Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Видео:Системы комплексных уравненийСкачать

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

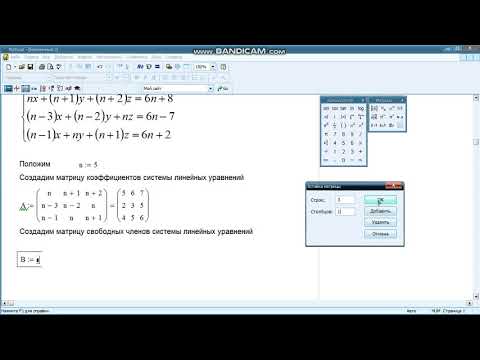
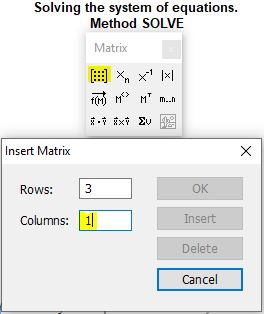
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

MathCAD — это просто! Часть 19. Немного о работе с комплексными числами

Комплексные числа — одна из важнейших математических абстракций, очень часто используемая в реальных расчетах инженерами, физиками, электронщиками и другими специалистами. Само собой, настолько важная часть математики, как работа с комплексными числами, не могла остаться вне поля зрения разработчиков MathCAD’а. Сегодня мы с вами как раз и поговорим о том, как можно работать в MathCAD’е с ними — вы сможете самостоятельно убедиться в том, что это, в общем-то, не представляет каких-либо особых сложностей для пользователя этого мощнейшего математического пакета.

Суть теории комплексных чисел заключается, по существу, в том, что множество действительных чисел можно расширить до другого, нового, множества (оно как раз таки и имеет название множества комплексных чисел), в котором каждое число представимо в виде z = a + b*i, где i — мнимая единица (корень из числа -1, или, вернее, один из корней). При этом a называется действительной частью комплексного числа (обозначается как Re(z)), а b, соответственно, принято называть его мнимой частью. Обозначается же мнимая часть комплексного числа как Im(z). Стоит отметить тот факт, что нередко даже образованные люди теряются, когда им нужно произнести вслух термин «комплексное число». На какую букву ставить ударение в слове «комплексный» — на «о» или «е»? Честно говоря, правильного ответа на этот вопрос я не знаю. Даже в математических словарях и справочниках нет единодушия: в некоторых ударение ставят на одну букву, в некоторых — на другую. Традиционно используют, впрочем, ударение на букву «е» (есть даже шутка такая: «комплексными бывают обеды, а числа — только комплексные»). Но если вы где-то скажете «комплексные числа», то в тюрьму вас за это, конечно же, никто не посадит. Фактически же комплексное число является упорядоченной парой действительных чисел, и часто даже вместо a + b*i записывают комплексные числа в виде (a; b). В ряде практических вычислений нужно оперировать именно такими упорядоченными парами чисел — например, в той же радиоэлектронике такой парой могут служить амплитуда и частота сигнала. Чем же в таком случае комплексное исчисление так принципиально отличается от векторного? В первую очередь, своим математическим аппаратом, позволяющим осуществлять с довольно большой степенью удобства некоторые преобразования над ними.

Существуют различные формы представления комплексного числа, каждая из которых удобна в своем виде операций над этими числами. Та форма, с которой мы с вами уже успели познакомиться, называется алгебраической формой, или алгебраическим представлением комплексного числа. Она удобна для того, чтобы такие числа суммировать (ну, и вычитать, конечно же, тоже). Действительная часть складывается с действительной, мнимая с мнимой, и все получается хорошо. Но вот умножать или возводить в степень комплексные числа в алгебраической форме уже, мягко говоря, не так удобно. Для этого используют тригонометрическую или экспоненциальную формы записи комплексных чисел. В общем-то, эти две формы фактически представляют собой одну и ту же форму записи, которую чаще все же называют тригонометрической. Получается она из алгебраической формы довольно-таки просто. Для начала нужно получить два параметра, с помощью которых комплексное число представляется в тригонометрической форме. Первый параметр называется модулем числа и вычисляется как корень из суммы квадратов a и b. Второй параметр принято называть аргументом комплексного числа z, и вычисляется он как арктангенс выражения b/a. Для любого из комплексных чисел переход от алгебраической формы к тригонометрической не представляет никакой сложности, поскольку формулы, по которым вычисляются и модуль, и аргумент, очень просты и для понимания, и для запоминания, и для применения. Само же комплексное число z записывается в тригонометрической форме следующим образом: z = r (cos? + i*sin?). Здесь r — это модуль комплексного числа z, а ? — соответственно, как вы уже навреняка успели догадаться, его же аргумент. Экспоненциальная форма записи комплексного числа — это, как я уже говорил, по сути, та же тригонометрическая, поскольку на множестве комплексных чисел экспонента ведет себя совсем не так, как на множестве чисел действительных. Фактически та формула для тригонометрической записи числа, которую я только что показал вам, с помощью экспоненты может быть записана гораздо короче: z = r*ei*?. Как видите, с использованием экспоненциального представления становится особенно просто умножать комплексные числа друг на друга, а также возводить их в степень. Для того, чтобы возводить в степень числа в тригонометрическом их представлении, можно воспользоваться формулой Муавра, которая безо всяких сложностей отыщется в любом справочнике по высшей математике.

Комплексные числа в MathCAD: основы

Весь тот небольшой экскурс в работу с комплексными числами, который я привел выше, нужен только для того, чтобы напомнить (или, если кто-то не знал этого, то разъяснить), что же такое комплексные числа, и как именно с ними нужно работать. При работе в MathCAD’е, само собой, вам не понадобится собственноручно вычислять модуль и аргумент комплексного числа, не надо будет самостоятельно высчитывать степень экспоненты при перемножении комплексных чисел и даже не понадобится самому складывать действительную часть с действительной, а мнимую — с мнимой. Все за вас сделает этот мощный математический пакет. То есть, конечно, не все, а только черновую, вычислительную работу — постановка задачи и интерпретация результатов вычислений все равно останется за вами. Хорошая новость состоит в том, что для работы с комплексными числами не нужно как-то по- особенному настраивать среду MathCAD или применять какие-то новые арифметические операторы. Среда точно так же работает с комплексными числами, как и с действительными. Простой пример — сложение комплексных чисел. Попробуйте сложить два комплексных числа — например, 1+2i и 7-15i. Здесь, правда, стоит отдельно сказать пару слов относительно ввода в MathCAD’е мнимой единицы. Дело в том, что, если вы просто напишете ее как i, нажав на клавиатуре соответствующую клавишу, то система MathCAD посчитает, что вы ввели имя какой-либо переменной. Поэтому можно либо воспользоваться панелью инструментов Calculator (см. иллюстрацию, на которой нужная кнопка обведена кружком), либо вводить с клавиатуры комбинацию 1i.

После того, как вы попробуете складывать комплексные числа, можно попробовать их перемножать, чтобы убедиться в том, что MathCAD умеет делать и это. Можете попробовать возводить комплексные числа в какую-либо степень, а также любым другим образом поиздеваться над ними. Как и следовало ожидать, MathCAD с легкостью справляется с подобными заданиями. Поэтому вы можете работать с комплексными числами фактически точно так же, как и с действительными.

Комплексные числа в MathCAD: подробности и тонкости

Впрочем, конечно же, есть и некоторые тонкие моменты, связанные с отличиями в работе с комплексными и действительными числами. Самое главное из подобного рода отличий состоит, собственно говоря, в том, что операция извлечения корня с ними работает не совсем так, как надо — как, впрочем, и операция возведения в дробную степень, хотя для действительных чисел данные операции и абсолютно корректны. Дело в том, что на множестве комплексных чисел мы рассматриваем корень p n-й степени из числа z как множество решений уравнения pn = z. Если вы попробуете решить это уравнение с помощью оператора solve (хоть о нем мы говорили уже достаточно давно — думаю, вы еще не до конца забыли, как им пользоваться), то увидите, что для n-й степени это уравнение, согласно основной теореме алгебры, будет иметь ровно n решений. Если же для вычисления корня комплексного числа вы воспользуетесь операторами извлечения корня или возведения комплексного числа в дробную степень, то увидите, что подобные вычисления дадут вам только один корень из всех возможных, что не вполне корректно. Впрочем, в ряде практических задач вам будет нужен только один корень, но все равно его лучше получать с помощью solve, а затем уже выбирать среди результатов.

Ну, и напоследок такой вопрос: а как лучше обозначать мнимую единицу? Дело в том, что в литературе встречается два варианта ее обозначения: i и j. Первый более характерен для советских и постсоветских источников, второй — для зарубежных. Вполне может случиться так, что вам потребуется в вашем проекте использовать второе, а не первое, которое используется в MathCAD по умолчанию. Конечно же, эта мощная математическая среда позволяет нам изменить обозначение мнимой единицы на то, которое будет для нас наиболее удобным. Для того, чтобы поменять обозначение, нужно в меню Format выбрать пункт Result, а в появившемся окне на вкладке Display Options заменить параметр Imaginary Value. Вариантов этого параметра, конечно, не много — собственно, их всего два: либо i, либо j. Но больше вариантов, собственно говоря, и нету.

Итак, мы с вами познакомились с комплексными числами, а также с тем, как именно работать с ними в MathCAD’е. Вы смогли сами убедиться, что это совсем несложно, хотя, конечно, некоторые вычисления и имеют свои тонкости. Но тонкости есть везде, и главное — быть заранее готовым к тому, что есть немалый шанс с ними столкнуться. Поэтому, если вы внимательно читаете статьи серии «MathCAD — это просто», то будете хорошо подготовлены к встречам с различными неожиданностями в среде MathCAD. Успехов вам в работе с этим мощным математическим пакетом и интересных вычислений!

Компьютерная газета. Статья была опубликована в номере 33 за 2008 год в рубрике soft