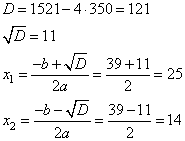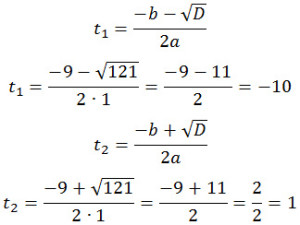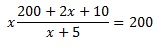Про уравнения - легко » Статьи

Решение системы уравнений огэ 21 задание

Обновлено
Разбор задания №21 ОГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Для решения данной системы можно вычесть второе уравнение из первого, это позволит избавиться от переменной y, получим:

Решение системы уравнений огэ 21 задание

Решаем квадратное уравнение через дискриминант, имеем два корня:

Решение системы уравнений огэ 21 задание

Для каждого из найденных корней найдем соответствующее значение y, подставив Решение системы уравнений огэ 21 заданиево второе уравнение:

Решение системы уравнений огэ 21 заданиеи Решение системы уравнений огэ 21 задание

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Так как оба уравнения равны одному и тому же значению y, то их можно приравнять, получим:

Решение системы уравнений огэ 21 задание,

Решение системы уравнений огэ 21 задание

Полученное выражение будет равно 0, если

Решение системы уравнений огэ 21 заданиеили Решение системы уравнений огэ 21 задание

Найдем теперь значения y для каждого x, имеем:

Решение системы уравнений огэ 21 заданиеи Решение системы уравнений огэ 21 задание

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Разделим первое уравнение на 2, а второе – на 4, получим:

Решение системы уравнений огэ 21 задание

Видим, что у обоих уравнений есть слагаемое Решение системы уравнений огэ 21 задание. Чтобы избавиться от него, вычтем из первого уравнения второе:

Решение системы уравнений огэ 21 задание

Теперь вычислим значение y при x=2, подставив x в первое уравнение, имеем:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание.

Таким образом, имеем решение (2, -2), (2,2).

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Разделим второе уравнение на 2, получим систему

Решение системы уравнений огэ 21 задание

и вычтем из первого уравнения второе:

Решение системы уравнений огэ 21 задание

Для значения x=2 найдем соответствующие значения y, подставив x в первое уравнение:

Решение системы уравнений огэ 21 задание

То есть имеем два решения: (2;-3) и (2;3).

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание

Преобразуем уравнение, приведем его к следующему виду:

Решение системы уравнений огэ 21 задание

Полученное выражение будет равно 0, если

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Таким образом, получили следующие корни: -4; -3; 2.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Упростим выражение, перепишем его в следующем виде:

Решение системы уравнений огэ 21 задание

Полученное выражение будет равно 0, если

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Получили три корня: -5; -4; 3.

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Сложим оба уравнения, получим:

Решение системы уравнений огэ 21 задание

Для найденных корней x вычислим из первой формулы соответствующие значения y, имеем:

— для Решение системы уравнений огэ 21 задание: Решение системы уравнений огэ 21 задание;

— для Решение системы уравнений огэ 21 задание: Решение системы уравнений огэ 21 задание.

Получили два решения: (-1;5), (1;5).

Задание 21. Решите систему уравнений Решение системы уравнений огэ 21 задание

Сложим оба уравнения, получим:

Решение системы уравнений огэ 21 задание

Вычислим соответствующие значения y при x=-2 и 2, подставив эти значения в первую формулу системы:

— при x=-2: Решение системы уравнений огэ 21 задание;

— при x=2: Решение системы уравнений огэ 21 задание.

Имеем следующие решения: (-2; 3) и (2; 3).

Задание 21. Решите неравенство Решение системы уравнений огэ 21 задание.

Можно заметить, что данное неравенство будет больше либо равно 0, если

Решение системы уравнений огэ 21 задание.

Преобразуем данное выражение, перепишем его в виде:

Решение системы уравнений огэ 21 задание

Из последнего выражения имеем две точки, делящие числовую ось:

Решение системы уравнений огэ 21 заданиеи Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание.

Ответ: Решение системы уравнений огэ 21 задание.

Задание 21. Решите неравенство Решение системы уравнений огэ 21 задание

Сложим оба уравнения системы, избавимся таким образом от переменной y, получим:

Решение системы уравнений огэ 21 задание

Теперь, для каждого из найденных x, вычислим y из первого уравнения:

Решение системы уравнений огэ 21 задание

Получаем решения: (-1; 8), (1; 8).

Задание 21. Решите неравенство Решение системы уравнений огэ 21 задание

Сложим оба уравнения системы, избавимся от переменной y, получим:

Решение системы уравнений огэ 21 задание

Для каждого найденного корня x вычислим соответствующее значение y из первого уравнения, имеем:

Решение системы уравнений огэ 21 задание

То есть получили следующие решения: (-2; 1), (2; 1).

Задание 21. Найдите значение выражения 28a-7b+40, если Решение системы уравнений огэ 21 задание.

Приведем выражение Решение системы уравнений огэ 21 заданиек виду Решение системы уравнений огэ 21 задание, получим:

Решение системы уравнений огэ 21 задание

Задание 21. Найдите значение выражения 33a-23b+71, если Решение системы уравнений огэ 21 задание.

Приведем выражение Решение системы уравнений огэ 21 заданиек выражению Решение системы уравнений огэ 21 задание, получим:

Решение системы уравнений огэ 21 задание

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Учитывая, что слагаемые в уравнении всегда больше либо равны 0, то уравнение будет равно нулю, если каждое из слагаемых равно нулю. Соответственно, получаем следующую систему уравнений:

Решение системы уравнений огэ 21 задание

Из первого уравнения имеем корни

Решение системы уравнений огэ 21 задание

Из второго уравнения, получаем следующие два корня:

Решение системы уравнений огэ 21 задание

Из полученных значений видно, что оба уравнения одновременно будут принимать значение 0 при x=-5.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Любое число в квадрате всегда больше 0, следовательно, уравнение будет равно 0, если оба слагаемых равны 0. Это условие можно записать в виде следующей системы:

Решение системы уравнений огэ 21 задание

Из первого уравнения получаем два корня:

Решение системы уравнений огэ 21 задание

Из второго уравнения, имеем корни:

Решение системы уравнений огэ 21 задание

Общий корень, при котором оба уравнения переходят в 0, равен -4.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Упростим уравнение, приведем его к следующему виду:

Решение системы уравнений огэ 21 задание

Данное уравнение будет равно 0, если

Решение системы уравнений огэ 21 задание

Решаем первое квадратное уравнение, получаем корни:

Решение системы уравнений огэ 21 задание

Оба корня удовлетворяют неравенству Решение системы уравнений огэ 21 задание, следовательно, они являются решениями уравнения.

Ответ: Решение системы уравнений огэ 21 задание.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Преобразуем уравнение к виду

Решение системы уравнений огэ 21 задание

Данное уравнение будет равно 0, если

Решение системы уравнений огэ 21 задание

Найдем корни уравнения из квадратного уравнения:

Решение системы уравнений огэ 21 задание

Оба корня не равны 0, следовательно, являются решениями уравнения.

Ответ: Решение системы уравнений огэ 21 задание.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Сначала преобразуем выражение, получим:

Решение системы уравнений огэ 21 задание

Последнее выражение показывает, что уравнение будет равно 0, если хотя бы один из множителей будет равен 0, то есть имеем 3 уравнения и 3 корня:

Решение системы уравнений огэ 21 задание

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Сначала выполним преобразование уравнения, получим:

Решение системы уравнений огэ 21 задание

Последнее выражение показывает, что уравнение будет равно, если хотя бы один из множителей равен 0, то есть имеем следующие три уравнения:

Решение системы уравнений огэ 21 задание

Задание 21. Решите неравенство Решение системы уравнений огэ 21 задание.

Преобразуем неравенство, приведем его к виду:

Решение системы уравнений огэ 21 задание

Полученное выражение дает две точки, делящие числовую ось:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание.

Ответ: Решение системы уравнений огэ 21 задание.

Задание 21. Решите неравенство Решение системы уравнений огэ 21 задание.

Перепишем неравенство в следующем виде:

Решение системы уравнений огэ 21 задание

Из последнего выражения имеем две точки, делящие числовую ось:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание.

Ответ: Решение системы уравнений огэ 21 задание.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Выполним следующее преобразование уравнения:

Решение системы уравнений огэ 21 задание

Полученное выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем три уравнения и три корня:

Решение системы уравнений огэ 21 задание

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Перепишем уравнение в следующем виде:

Решение системы уравнений огэ 21 задание

Последнее выражение принимает нулевое значение, когда хотя бы один из множителей равен 0, то есть имеем три следующих корня:

Решение системы уравнений огэ 21 задание

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Решим уравнение при условии, что Решение системы уравнений огэ 21 задание, получим:

Решение системы уравнений огэ 21 задание

Решим квадратное уравнение с помощью дискриминанта, имеем:

Решение системы уравнений огэ 21 задание

Значение 7 не входит в диапазон Решение системы уравнений огэ 21 задание, остается только один корень -5.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

1. Запишем ОДЗ уравнения:

Решение системы уравнений огэ 21 задание

2. Упростим уравнение, приведем его к виду:

Решение системы уравнений огэ 21 задание

Решаем квадратное уравнение, имеем два корня:

Решение системы уравнений огэ 21 задание

Из двух корней только второй Решение системы уравнений огэ 21 заданиепринадлежит ОДЗ.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Так как каждое из слагаемых всегда больше либо равно 0, то уравнение будет равно нулю только если оба слагаемых равны 0, то есть данное уравнение можно записать в виде следующей системы:

Решение системы уравнений огэ 21 задание

Упрощаем данные выражения, имеем:

Решение системы уравнений огэ 21 задание

Имеем один общий корень -3, при котором оба уравнения одновременно равны 0, то есть этот корень есть решение уравнения.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Каждое из слагаемых уравнения всегда больше либо равно 0, следовательно, уравнение будет равно 0, только если оба слагаемых равны 0. Запишем это положение в следующем виде:

Решение системы уравнений огэ 21 задание

Упростим выражения, получим:

Решение системы уравнений огэ 21 задание

Первое уравнение дает два корня

Решение системы уравнений огэ 21 задание

Второе уравнение также дает два корня:

Решение системы уравнений огэ 21 задание

В результате получаем один общий корень Решение системы уравнений огэ 21 задание, при котором оба уравнения одновременно равны 0.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Упростим выражение, запишем его в виде:

Решение системы уравнений огэ 21 задание

Последнее выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем два уравнения:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Таким образом, получили три корня уравнения -2; -1; 1.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

Перепишем уравнение в следующем виде:

Решение системы уравнений огэ 21 задание

Последнее выражение будет равно 0, если хотя бы одна из скобок будет равна 0, то есть имеем следующие два уравнения:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Таким образом, получили три корня уравнения -5; -2; 2.

Задание 21. Найдите значение выражения 61a-11b+50, если Решение системы уравнений огэ 21 задание.

Упростим выражение Решение системы уравнений огэ 21 задание, перепишем его в следующем виде:

Решение системы уравнений огэ 21 задание

Чтобы привести выражение к виду Решение системы уравнений огэ 21 задание, прибавим к левой и правой части уравнения 10, получим:

Решение системы уравнений огэ 21 задание

То есть получили значение 10.

Задание 21. Найдите значение выражения 39a-15b+25, если Решение системы уравнений огэ 21 задание.

Преобразуем выражение Решение системы уравнений огэ 21 заданиек виду

Решение системы уравнений огэ 21 задание

Чтобы получить выражение вида Решение системы уравнений огэ 21 заданиеприбавим к левой и правой части уравнения 1, получим:

Решение системы уравнений огэ 21 задание

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

1. Запишем ОДЗ уравнения

Решение системы уравнений огэ 21 задание

2. Упростим уравнение, получим:

Решение системы уравнений огэ 21 задание

Решаем квадратное уравнение, имеем два корня:

Решение системы уравнений огэ 21 задание

ОДЗ удовлетворяет только один корень -3.

Задание 21. Решите уравнение Решение системы уравнений огэ 21 задание.

1. ОДЗ уравнения

Решение системы уравнений огэ 21 задание

2. Упростим уравнение, получим:

Решение системы уравнений огэ 21 задание

Решаем квадратное уравнение, имеем два корня:

Решение системы уравнений огэ 21 задание

ОДЗ принадлежит только один корень уравнения -3.

Задание 21. Найдите значение выражения 19a-7b+12, если Решение системы уравнений огэ 21 задание.

Перепишем выражение Решение системы уравнений огэ 21 заданиев виде:

Решение системы уравнений огэ 21 задание

Приведем последнее выражение к виду Решение системы уравнений огэ 21 задание, получим:

Решение системы уравнений огэ 21 задание

Задание 21. Найдите значение выражения 25a-5b+22, если Решение системы уравнений огэ 21 задание.

Упростим выражение Решение системы уравнений огэ 21 задание, получим:

Решение системы уравнений огэ 21 задание

Чтобы привести последнее выражение к виду Решение системы уравнений огэ 21 задание, добавим к выражению 4:

Решение системы уравнений огэ 21 задание

Решение системы уравнений огэ 21 задание

Курс повышения квалификации

Содержание
  1. Дистанционное обучение как современный формат преподавания
  2. Математика: теория и методика преподавания в образовательной организации
  3. Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
  4. Дистанционные курсы для педагогов
  5. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  6. Другие материалы
  7. Вам будут интересны эти курсы:
  8. Оставьте свой комментарий
  9. Автор материала
  10. Дистанционные курсы для педагогов
  11. Подарочные сертификаты
  12. ЗАДАЧА 21 огэ
  13. Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ЕГЭ, более сложные встретятся если «не повезло».
  14. Сложность 1 (легкие задачи)
  15. Сложность 2 (средние по сложности задачи)
  16. Сложность 3 (более сложные задачи)
  17. Задание №21 ОГЭ по математике
  18. 💡 Видео

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 949 человек из 80 регионов

Решение системы уравнений огэ 21 задание

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 681 человек из 75 регионов

Решение системы уравнений огэ 21 задание

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

  • Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:ОГЭ задача 21 (системы уравнений) #3Скачать

ОГЭ задача 21 (системы уравнений) #3

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 566 193 материала в базе

Другие материалы

  • 26.09.2019
  • 132
  • 0

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 187
  • 0

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 261
  • 11

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 539
  • 28

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 157
  • 0
  • 26.09.2019
  • 211
  • 1

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 691
  • 7

Решение системы уравнений огэ 21 задание

  • 26.09.2019
  • 152
  • 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 26.09.2019 2078
  • DOCX 138.9 кбайт
  • 97 скачиваний
  • Рейтинг: 5 из 5
  • Оцените материал:

Настоящий материал опубликован пользователем Шамченко Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Решение системы уравнений огэ 21 задание

  • На сайте: 2 года и 4 месяца
  • Подписчики: 1
  • Всего просмотров: 24962
  • Всего материалов: 31

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:21 задание из ОГЭ по математике 2024. Текстовые задачиСкачать

21 задание из ОГЭ по математике 2024. Текстовые задачи

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Решение системы уравнений огэ 21 задание

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Решение системы уравнений огэ 21 задание

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Решение системы уравнений огэ 21 задание

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Решение системы уравнений огэ 21 задание

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Решение системы уравнений огэ 21 задание

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Решение системы уравнений огэ 21 задание

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Решение системы уравнений огэ 21 задание

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | Математика

ЗАДАЧА 21
огэ

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ЕГЭ, более сложные встретятся если «не повезло».

Сложность 1 (легкие задачи)

    Мастер выполняет заказ на детали за 4 часа. Ученик мастера выполняет такой же заказ за 5 часов. За сколько часов выполнят девять таких заказов мастер и ученик, работая вместе?

Моторная лодка проплыла против течения реки 20 км. После этого мотор вышел из строя, и лодку отнесло течением реки на место старта. На весь путь туда и обратно лодка затратила 6 часов. Найдите скорость лодки в стоячей воде, если скорость течения реки 5 км/ч. Ответ дайте в км/ч.

В 5% раствор кислоты объемом 6 литров добавили 2 литра воды и 4 литра 9% раствора. Сколько процентов составляет концентрация кислоты в получившемся растворе?

Рубашка после двух подорожаний стала стоить 660 рублей, причем первый раз она подорожала на 10%, а второй раз — на 20%. Сколько стоила рубашка до первого подорожания?

Моторная лодка отчалила от пристани и проплыла против течения реки 40 км. После остановки на 30 минут лодка повернула обратно. В пункт отправления лодка приплыла через шесть с половиной часов после отплытия. Найдите скорость лодки в стоячей воде, если скорость течения реки 5 км/ч. Ответ дайте в км/ч.

Пуля, вылетев из ружья, пролетела 30 метров с постоянной скоростью и попала в мишень. Пробив мишень насквозь, пуля потеряла две трети своей скорости и, пролетев еще 10 метров, врезалась в отбойник. Найти начальную скорость пули в м/с, если время полета пули из ружья до отбойника составило 0,1 с.

Грузовая машина выехала из пункта А и должна доехать до пункта В в назначенное время. Однако ровно на середине пути ей пришлось остановиться на 25 минут из-за поломки. Чтобы прибыть в пункт В в назначенное время, машине пришлось увеличить скорость на 10 км/ч. Найдите скорость машины до поломки, если расстояние между А и В составляет 100 км.

В банке находится 5 литров 20-ти процентного раствора вещества. Сколько литров 50-ти процентного раствора того же вещества надо долить в банку, чтобы получился 44-х процентный раствор?

В начальный момент времени часы со стрелками показывают 8 часов 20 минут. Сколько раз до 12 часов 30 минут этого же дня минутная стрелка поравняется с часовой?

Моторная лодка проплыла по течению реки 10 км. После этого мотор вышел из строя, и лодку несло течением еще 2 километра. На весь путь лодка затратила 1,5 часа. Найдите скорость течения реки, если скорость лодки по течению реки 20 км/ч. Ответ дайте в км/ч.

Два друга Андрей и Сергей отвечают на одинаковые вопросы тестового экзамена. Андрей отвечает на 8 вопросов в час, Сергей на 6 вопросов в час. Экзамен они начали одновременно. Андрей ответил на все вопросы экзамена раньше Сергея на 40 минут. Сколько вопросов было в тестовом экзамене?

Весь путь путешественника разбит на три равных по длине отрезка. Первый отрезок пути путешественник прошел пешком со скоростью 5 км/ч. Второй отрезок пути проехал на лошади со скоростью 10 км/ч. Третий участок пути путешественник должен проплыть на плоту по реке. Какова скорость плота, если средняя скорость путешественника на всем пути оказалась равной 3,75 км/ч.

Пуля после попадания в мишень теряет две трети своей скорости и пролетев некоторое расстояние врезается в отбойник. В начальный момент выстрела расстояние от пули до отбойника составляет 200 метров, от мишени до отбойника – 50 метров. Какой должна быть начальная скорость пули в м/с, если средняя скорость пули на всем пути до отбойника оказалась равной 300 м/с.

При сушке абрикосов на солнце 85% первоначального веса испаряется и получается курага. Сколько килограммов абрикосов надо взять для получения 9 килограммов кураги?

Семь чисел образуют арифметическую прогрессию. Сумма первого и последнего равна 6, а сумма второго и третьего равна 0. Найдите пятое число.

Маша путь от своего дома до дома Мишки прошла со скоростью 100 метров/минуту, а обратно она ехала на велосипеде со скоростью 150 метров/минуту. Найдите среднюю скорость Маши на всем пути. Ответ дайте в метрах в минуту.

Пуля после попадания в мишень теряет две трети своей скорости и пролетев некоторое расстояние врезается в отбойник. В начальный момент выстрела расстояние от пули до отбойника составляет 100 метров. Начальная скорость пули – 800 м/с. На каком расстоянии (в метрах) от отбойника была установлена мишень, если средняя скорость пули на всем пути до отбойника оказалась равной 500 м/с.

Турист прошел четверть пути со скоростью 5 км/ч, потом по холмам он прошел еще четверть путь со скоростью 4 км/ч, затем еще четверть пути проехал на велосипеде со скоростью 20 км/ч и последнюю четверть пути проехал на попутном автобусе со скоростью 30 км/ч. Найдите среднюю скорость туриста на всем пути. Ответ дайте в км/ч.

Сложность 2 (средние по сложности задачи)

    Винни-Пух съедает банку меда за 4 часа. Его друг Пятачок съедает половину такой же банки меда за 8 часов. За сколько минут они съедят банку меда вместе?

Винни-Пух съел половину горшочка меда за 40 минут, после чего к нему зашел его друг Пятачок и оставшиеся полгоршочка они доели за 30 минут вместе. Винни-Пух подарил Пятачку на день рождение такой же горшочек меда. За сколько часов может съесть один Пятачок этот горшочек?

Прямолинейный путь букашки разбит на пять равных по длине частей. Скорость букашки на первом участке равна 0,25 м/с. Скорость на втором участке в два раза больше. Скорость букашки на каждом следующем участке в два раза больше чем на предыдущем. Найдите среднюю скорость букашки на всем пути. Ответ дайте в м/с и округлите до десятых.

Цена брюк на 20% больше цены джинсовой рубашки. Джинсовая рубашка стоит 750 рублей. Определите, на сколько процентов трое брюк дешевле четырех рубашек.

Первая труба наполняла бассейн в одиночку два часа. Затем включилась вторая и, проработав вместе еще 4 часа, они наполнили бассейн. Первая труба в одиночку наполняет бассейн в полтора раза быстрее чем вторая, также работающая одна. За сколько часов две трубы вместе наполнят бассейн?

Два велосипедиста одновременно стартуют из диаметрально противоположных точек круговой трассы и двигаются в одном направлении. Скорость первого в полтора раза больше скорости второго. Через сколько минут первый велосипедист догонит второго, если длина трассы 10 километров, а скорость второго велосипедиста равна 20 км/ч?

Первую половину пути катер прошел по течению узкой части реки с большой скоростью течения. После излучины русло реки расширилось, и течение стало в два раза медленнее. Найдите скорость течения в начале пути, если на первую половину потребовалось в 1,2 раза меньше времени. Скорость катера в стоячей воде 20 км/ч. Ответ дайте в км/ч.

Винни-Пух и Кролик должны съесть на время одинаковое количество горшочков с медом. Винни-Пух съедает 4 горшочка за 45 минут. Кролик съедает 6 горшочков за полтора часа. Винни-Пух съел все свои горшочки раньше Кролика на 1 час 15 минут. Сколько горшочков было у каждого?

Пароход длиной 100 метров и баржа длиной 200 метров двигаются по озеру параллельными курсами и в одном направлении. В начальный момент пароход находится позади баржи и расстояние от его носовой части до кормы баржи составляет 5 км. Корма парохода поравняется с носом баржи через 30 минут. Найти скорость баржи, если скорость парохода 25 км/ч. Ответ дайте в км/ч.

В емкости находится 5 литров 20% раствора соли. Какой объем сухой соли (в литрах) необходимо засыпать в емкость, чтобы концентрация соли в емкости стала 84%? Дайте ответ с учетом того, что при засыпании сухой соли в емкость 20% соли просыпается мимо.

В некотором магазине рубашка дорожала дважды, первый раз на 12%, а второй раз — на 20%. Сколько рублей стоила рубашка до первого подорожания, если в общей сложности она подорожала на 86 рублей?

Из пунктов A и B, расстояние между которыми 87,5 км, одновременно навстречу друг другу выехали два автомобиля. Первый ехал со скоростью 50 км/ч. Каждый из автомобилей, повстречав друг друга первый раз, не останавливаясь, поехал дальше. Первый автомобиль, доехав до пункта В, развернулся и поехал обратно. Второй автомобиль, доехав до пункта А, остановился на полчаса и также поехал обратно. Второй раз автомобили повстречались через 3 часа после отправления из начальных пунктов. Найдите скорость (в км/ч) второго автомобиля.

Машина с почтой выехала из пункта А и должна доехать до пункта В в назначенное время. Однако, проехав 5,5 километров, машина была вынуждена вернуться обратно, чтобы взять позабытую посылку. Чтобы прибыть в пункт В в назначенное время, машине пришлось увеличить скорость на 5 км/ч. Найдите запланированную скорость машины, если расстояние между А и В составляет 132 км.

В первой банке объемом 5 литров находится раствор некторого вещества. Во второй банке объемом 8 литров находится другой раствор того же вещества. Если слить вместе обе банки, то в получившимся растворе концентрация вещества будет 12%. Если бы в первой банке было 10 литров такого же раствора что был в ней изначально, а во второй банке ничего не изменилось, то в результате получился бы раствор с концентрацией 10%. Найдите концентрацию вещества во второй банке. Ответ дайте в процентах.

В первом и во втором баках одинакового объема находится 15% растворы некоторого вещества. В третьем баке находится 30% раствор этого же вещества. Если слить вместе все три бака, то концентрация вещества будет 25%. Во сколько раз объем первого бака меньше объема третьего?

Сухогруз с собственной скоростью 15 км/ч отплыл от причала А и плыл по течению реки два часа, после чего сообщил о поломке двигателя. От причала А сразу отплыл буксир длиной 100 метров и с собственной скоростью 20 км/ч. Через час после отплытия буксир еще не догнал сухогруз, и расстояние между его носом и кормой сухогруза составляло 16 км. Найдите скорость течения реки, если сухогруз после поломки дрейфовал со скоростью течения. Ответ выразите в км/ч. (В момент отплытия обоих судов у причала находится корма (задняя часть судна).

Пешеход прошел четверть пути со скоростью 6 км/ч, потом по неровной дороге он прошел еще четверть путь со скоростью 4 км/ч, затем еще четверть пути проехал на велосипеде со скоростью 15 км/ч и последнюю четверть пути проехал на маршрутке со скоростью 60 км/ч. Найдите, на сколько км/ч средняя скорость на первом и втором участках (рассматриваются как один путь) меньше средней скорости на всем пути.

Два пешехода вышли навстречу друг другу из пунктов А и В, расстояние между которыми 10 км. Через два часа они встретились, потратили на разговор 15 минут и пошли дальше каждый в своем старом направлении. Найдите скорость второго пешехода, если первый прибыл в пункт В через 2 часа 55 минут после выхода из А. Ответ дайте в в км/ч.

В первом сосуде находится 25% раствор спирта. Во втором сосуде находится 20% раствор спирта. Если слить вместе эти два раствора и добавить 2 литра чистого спирта, то полученная концентрация будет 26%. Если же слить вместе в два раза больший объем 25% раствора тот же объем 20% и добавить 2 литра чистой волы, то концентрация спирта будет такой же, как во втором сосуде. Найдите объем меньшего сосуда. Ответ дайте в литрах.

Моторная лодка отчалила от пристани и проплыла по течению реки 61,5 км. После остановки на 30 минут лодка повернула обратно. Через 5,5 часов после начала движения от пристани лодке оставалось плыть до нее 30,5 километров. Скорость лодки в стоячей воде 18 км/ч. Найти скорость течения реки, если известно, что она менее 3 км/ч. Ответ дайте в км/ч.

В первом баке находится 10% раствор некоторого вещества. Во втором баке находится 30% раствор этого же вещества. Если слить вместе два бака 10% раствора, один бак 30% раствора и добавить еще два литра воды, то концентрация вещества будет 20%. На сколько литров объем первого бака меньше объема второго?

Если моторная лодка движется против течения реки от пристани А до пристани В, то она преодолевает этот путь за 8 часов. Отплыв от пристани А к пристани В, лодка не доплыла до В 20 км и повернула обратно, и через 11 часов 5 минут вернулась в пункт А. Найти скорость лодки в стоячей воде, если скорость течения реки 2 км/ч.

Один мальчик красит картинку за 4 мин, а второй мальчик – за 6 мин. Они решили вместе покрасить картинку. Есть два способа покрасить картинку вдвоем: первый способ – каждый красит ровно половину картинки (и закончивший красить свою половину просто ждет другого), второй способ – красить всю картинку вместе от начала до конца. Насколько больше минут потребуется для покраски картинки первым способом?

Два соседних эскалатора одинаковой длины движутся один вверх, другой вниз с одинаковыми скоростями. Человек, стоя неподвижно, поднимается вверх по одному эскалатору за 12 секунд. Если человек идет вниз по второму (который двигается вниз) эскалатору, то это занимает 8 секунд. Сколько секунд потратил бы этот же человек, если бы поднимался вверх по неподвижному эскалатору? Скорость человека считается постоянной.

Четыре числа образуют возрастающую геометрическую прогрессию. Сумма первого и четвертого равна 56. Сумма второго и третьего равна 24. Найдите сумму первых двух.

Несколько чисел образуют арифметическую прогрессию. Разность прогрессии равна 2, а сумма всех членов прогрессии равна 108. Сколько членов в этой прогрессии, если сумма первого и пятого равна 16?

Первый конвейер выпускает в полтора раза больше упаковок орехов в час, чем второй. Работая вместе, эти два конвейера выполнили половину некоторого заказа, затем первый аппарат сломался и работу над заказом продолжил один второй. Из скольких упаковок орехов состоял весь заказ, если известно, что второй аппарат в итоге изготовил на 840 упаковок больше первого?

Две команды велосипедистов, состоящие каждая из двух человек, стартуют одновременно и в одном направлении из одной точки круговой трассы. Скорость первого номера первой команды больше скорости первого номера второй команды на 2 км/ч. Проехав по 45 минут каждый, первые номера каждой команды сменились вторыми. Найдите на сколько км/ч скорость второго номера второй команды больше скорости второго номера первой команды, если до финиша оба вторых номера доехали одновременно и ехали 30 минут.

Цена трех кепок меньше цены двух футболок на 45%. Разница в стоимости между тремя футболками и двумя кепками составляет 1020 рублей. Найдите на сколько рублей футболка дороже кепки.

Сложность 3 (более сложные задачи)

    Из пунктов A и B, расстояние между которыми 140 километров, одновременно навстречу друг другу выехали два автомобиля. Первый ехал со скоростью 30 км/ч, второй — со скоростью 40 км/ч. Каждый из автомобилей, повстречав друг друга первый раз, не останавливаясь, поехал дальше. Доехав до пунктов В и А соответственно, они развернулись и поехали обратно. На каком расстоянии от пункта В они встретятся второй раз?

Человек поднимается по стоящему эскалатору за 12 секунд. Если человек стоит на поднимающемся вверх эскалаторе, то он поднимется за 8 секунд. За сколько секунд этот же человек поднимется, если будет идти по движущемуся вверх эскалатору?

Два велосипедиста стартуют одновременно и в одном направлении из одной точки круговой трассы длины 10 км. Скорость первого из них на 3 км/ч больше скорости второго. Через какое время первый велосипедист обгонит второго на полтора круга? Ответ дайте в минутах.

Два велосипедиста стартуют одновременно и в одном направлении из одной точки круговой трассы длины 10 км. Первый велосипедист проезжает круг на 6 минут быстрее второго. Найдите скорость первого велосипедиста в км/ч, если он обгоняет второго на круг за 2 часа.

В гости к Кролику пришли Пятачок и Винни-Пух. Кролик планирует угощать гостей медом. Винни за минуту съедает 0,2 горшочка с медом, Кролик – 1/8 горшочка, а Пятачок – всего 1/40. Кролик уже знает, что если Винни-Пух съест хоть немного больше 4-х горшочков меда, то застрянет. Какое максимальное количество горшочков может поставить на стол Кролик, если он не хочет, чтобы Винни-Пух застрял? В задаче предполагается, что все трое начинают есть одновременно. Каждый берет себе по горшочку и ест только из него, а как только горшочек у кого-то заканчивается, тот берет себе следующий при его наличии.

Четыре мастера выкладывают стену за 4 часа. Если работают первый, второй и третий мастера, то они сделают эту работу за 6 часов, а второй, третий и четвертый мастера выполнят тот же объем работы за 5 часов. За сколько часов справятся с работой первый и четвертый мастера?

При старте из одной точки и в одном направлении по круговой трассе первый велосипедист обгоняет второго каждые два часа. Через сколько минут первый велосипедист второй раз обгонит второго, если они стартовали из диаметрально противоположных точек в одном направлении?

Пароход длиной 80 метров и баржа длиной 120 метров двигаются по озеру параллельными курсами и в одном направлении. В начальный момент пароход находится позади баржи и расстояние от его носовой части до кормы баржи составляет 9 километров 800 метров. Если пароход будет двигаться с той же скоростью, то его корма поравняется с носом баржи через 2 часа. Если же пароход увеличит скорость в полтора раза, то его нос поправляется с кормой сухогруза через 39,2 минуты. Найдите скорость баржи. Ответ дайте в км/ч.

Два пешехода вышли навстречу друг другу из пунктов А и В, расстояние между которыми 10 км. Через два часа они встретились, второй сразу пошел дальше, а первый потратил 10 минут на разговор по телефону и также отправился в своем старом направлении. Найдите скорость второго пешехода, если он прибыл в пункт А на 1 час 30 минут позже, чем первый прибыл в В. Ответ дайте в в км/ч.

Первый и второй велосипедисты выехали навстречу друг другу из различных пунктов А и В соответственно. Они встретились на расстоянии 18 км от В и, не останавливаясь, поехали дальше. Доехав до пунктов В и А соответственно, они развернулись и поехали обратно. Второй раз они встретились на расстоянии 24 км от А. Найти расстояние между пунктами А и В.

Пуля, вылетев из ружья, пролетела 28 метров с постоянной скоростью и попала в мишень. Пробив мишень насквозь, пуля потеряла часть своей скорости и, пролетев еще 15 метров, врезалась в отбойник. Время полета пули из ружья до отбойника составило 0,08 секунды. Если бы от мишени до отбойника было бы не 15, а 6 метров, то общее время полета пули составило 0,06 секунды. Найти отношение скорости пули после мишени к ее скорости до мишени (считается, что эта величина постоянна).

В гости к Кролику пришли Пятачок и Винни-Пух. Винни за минуту съедает 0,2 горшочка с медом, Пятачок – 1/9 горшочка, а Кролик – всего 1/45. Кролик уже знает, что если Винни-Пух съест больше 4-х горшочков меда, то застрянет. Какое максимальное количество горшочков может поставить на стол Кролик, если он не хочет, чтобы Винни-Пух застрял? В задаче предполагается, что все трое начинают есть одновременно и едет все вместе из одного горшочка, а как только он заканчивается – берут следующий.

Доход некоторой семьи складывается из зарплаты мужа, жены и сына-студента. Если зарплату мужа увеличить на 50%, то общий доход семьи увеличится на 32%. Если же зарплату жены уменьшить вдвое, а зарплату мужа уменьшить на 25%, то доход семьи уменьшится на 32%. Во сколько раз зарплата мужа больше зарплаты жены.

Доход некоторой семьи складывается из зарплаты мужа, жены и дочери-студентки. Если зарплату мужа увеличить в полтора раза, а стипендию дочери увеличить в 6 раз, то общий доход семьи увеличится на 52%. Если же зарплату жены уменьшить вдвое, а зарплату мужа уменьшить на 50%, то доход семьи уменьшится на 48%. Какой процент в общем доходе семьи составляет зарплата жены.

Первая бригада рабочих прокладывает дорогу за 3 часа. Если к этой бригаде присоединить вторую бригаду, то вместе они прокладывают дорогу в полтора раза длиннее за 2 часа. Теперь эти бригады с разных сторон начинают строить дорогу длиной 225 км. Сколько километров дороги придется построить второй бригаде?

В одной емкости находится 90 мл кофе, в другой емкости 80 мл молока. Из второй емкости 60 мл молока перелили в первую. Затем из первой емкости 80 мл смеси молока и кофе перелили во вторую. Что больше: концентрация молока в первой емкости или кофе во второй емкости? В ответе запишите большую концентрацию, выраженную в процентах.

Для изготовления изюма взяли некоторое количество винограда и высушили на солнце. Известно, что при сушке на солнце виноград теряет 80% первоначального веса. Половину полученной партии изюма поместили в герметичную упаковку и подготовили к транспортировке. Во время транспортировки упаковка была повреждена, и изюм вобрал в себя влагу из воздуха. В результате его масса увеличилась на 10%. После транспортировки изюм взвесили и получили 8,8 кг. Сколько килограмм винограда изначально высушили на солнце?

Два соседних эскалатора одинаковой длины движутся один вверх, другой вниз с одинаковыми скоростями. Человек, стоя неподвижно, поднимается вверх по одному эскалатору за 12 секунд. Если человек идет вниз по второму (который двигается также вниз) эскалатору, то это занимает 8 секунд. В некоторый день скорость эскалатора уменьшили в два раза; сколько секунд потратит человек в этот день при подъеме вверх по движущемуся вверх эскалатору? Скорость человека считается постоянной.

Несколько чисел образуют арифметическую прогрессию. Сумма первого и пятого членов прогрессии равна 18, а сумма второго и восьмого 46. Сколько членов в этой прогрессии, если сумма всех членов прогрессии равна 265?

Баржа длиной 80 метров и пароход идут параллельными курсами в одном направлении. Капитан парохода издал три гудка с интервалом в 5 минут между каждым гудком. Известно, что в момент первого гудка пароход отстает от баржи и расстояние между его носом и кормой баржи равно 120 метров. В момент второго гудка нос парохода поравнялся с носом баржи. А в момент третьего гудка расстояние между носом баржи и кормой парохода равно 150 метров. Найдите длину парохода. Ответ укажите в метрах.

Первый аппарат изготавливает в час в два раза больше кексов, чем второй. Работая вместе, эти два аппарата выполнили половину заказа, а затем первый аппарат сломался, и работу над заказом продолжил только второй. Известно, что второй аппарат в итоге изготовил на 700 кексов больше первого. Общее время выполнения заказа составило 20 часов. На сколько кексов больше в час изготавливал первый аппарат по сравнению со вторым?

Скорость парохода (длиной 100 метров) больше скорости баржи (длиной 250 метров) на 2,5 км/ч. В начальный момент времени пароход и баржа двигаются параллельными курсами навстречу друг другу, и расстояние между их носовыми частями – 800 метров. Какова скорость баржи, если через полчаса расстояние между их кормовыми частями (крайняя задняя точка) частями составило 18,1 км. Ответ дайте в км/ч.

Две команды велосипедистов, состоящие каждая из двух человек, стартуют одновременно и в одном направлении из одной точки круговой трассы. Скорость первого номера первой команды больше скорости первого номера второй команды на 2 км/ч. Через 90 минут первый номер догнал второго и, проехав еще 15 минут после этого, первые номера каждой команды сменились вторыми. Найдите на сколько км/ч скорость второго номера второй команды больше скорости второго номера первой команды, если до финиша оба вторых номера доехали одновременно и ехали 1,5 часа.

Если два велосипедиста стартуют одновременно и в одном направлении из диаметрально противоположных точек круговой трассы длиной 10 км, то один догоняет другого за 20 минут. Если же они стартуют одновременно и в разных направлениях из диаметрально противоположных точек этой же трассы, то они встречаются пятый раз через 50 минут. Найдите скорости велосипедистов. В ответе укажите большую из них, ответ дайте в км/ч.

Первый велосипедист стартовал из точки А круговой трассы длиной 24 км. Через 10 минут из точки В, диаметрально противоположной точке А, в том же направлении выехал второй велосипедист. Найдите скорость (в км/ч) первого велосипедиста, если известно, что он догнал второго через 15 минут после начала движения второго и прибыл в точку А раньше второго велосипедиста на 30 минут.

Первый велосипедист стартовал из точки А круговой трассы длиной 20 км. Через 5 минут из точки В, диаметрально противоположной точке А, навстречу первому выехал второй велосипедист. Найдите скорость (в км/ч) второго велосипедиста, если известно, что велосипедисты встретились первый через 10 минут после выезда второго, а второй раз – через 39 минут после выезда первого.

Имеется некоторый раствор соли в воде. Вес раствора 5 кг и концентрация соли в нем равна 20%. Сколько килограмм соли необходимо засыпать в емкость, чтобы концентрация соли стала 65%? Дайте ответ с учетом того, что при засыпании соли в емкость 10% соли просыпается мимо, и, кроме этого, засыпаемая соль уже имеет в себе 10% воды.

Обычно Иван Иванович проходит треть своего пути со скоростью 5 км/ч; далее дорога идет в гору, и следующую треть Иван Иванович проходит со
скоростью 3 км/ч. Последнюю треть пути Иван Иванович шел со своей обычной скоростью 6 км/ч, однако на середине этого участка полил дождь и Иван Иванович сел на автобус и за 9 минут доехал до конечной точки маршрута. Найдите среднюю скорость Ивана Ивановича на всем пути, если обычно (с такой же скоростью на каждом участке, но без проезда на автобусе) время в пути составляет 2,1 часа. Ответ укажите в км/ч.

Видео:Задание 21. Уравнения и системы уравнений. Подготовка к ОГЭ 2020. Вебинар | МатематикаСкачать

Задание 21. Уравнения и системы уравнений. Подготовка к ОГЭ 2020. Вебинар | Математика

Задание №21 ОГЭ по математике

В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.

Алгоритм решения:
  1. Введем неизвестную величину: скорость третьего.
  2. Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
  3. Выясняем, на какой

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение:

1. Обозначим через x км/ч скорость третьего велосипедиста. 2. Составим таблицу их краткого условия:

v, км/чt, чS, км
1 велосипедист21На 2 ч раньше всех
2 велосипедист15На 1 ч раньше третьего
3 велосипедистх

3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.

4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя 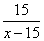Решение системы уравнений огэ 21 заданиеч после своего выезда.

Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через 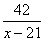Решение системы уравнений огэ 21 заданиеч после своего выезда из поселка.

По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.

5. Исходя из этого, составим равенство:

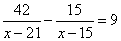
Решение системы уравнений огэ 21 задание,

Преобразуем полученное уравнение: Решение системы уравнений огэ 21 задание

6. Получили квадратное уравнение. Решим его:

Решение системы уравнений огэ 21 задание

По условию скорость третьего велосипедиста была наибольшей, значит, второй

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:
  1. Введем неизвестные величины: скорость третьего и время его движения.
  2. Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
  3. Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
  4. Исходя из условия, составляем равенства.
  5. Составляем и решаем систему уравнений.
  6. Определяем величины, которые еще нужно найти.
  7. Записываем ответ.
Решение:

1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.

2. Составим таблицу данных условия:

v, км/чt, чs, км
1 велосипедист15t +7
2 велосипедист10t +1
3 велосипедистхt

3. До места встречи со вторым велосипедистом третий проехал x·t км.

Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).

Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.

Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.

Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)

4. Составляем систему уравнений:

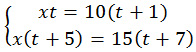
Решение системы уравнений огэ 21 задание5. Решаем полученную систему, преобразовав каждое из уравнений: Решение системы уравнений огэ 21 заданиеВычитаем из второго уравнение первое, получаем

Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.

(t + 19)·t = 10t + 10

t 2 + 19t = 10t + 10

По формуле дискриминанта и корней:

D = 9 2 — 4·1·(-10) = 81 + 40 = 121

Решение системы уравнений огэ 21 задание

Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,

x = t + 19 = 1 + 19 = 20

Скорость третьего велосипедиста 20 км/ч.

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:
  1. Введем неизвестные величины: скорость третьего и время его движения.
  2. Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
  3. Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
  4. Исходя из условия, составляем равенства.
  5. Составляем и решаем систему уравнений.
  6. Определяем величины, которые еще нужно найти.
  7. Записываем ответ.
Решение:

1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста. 2. Составим таблицу данных условия:

v, км/чt, чs, км
1 велосипедист24t +9
2 велосипедист21t +1
3 велосипедистхt

3. До места встречи со вторым велосипедистом третий проехал x·t км. Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км. Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1). Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км. Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км. Расстояния одинаковы. 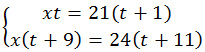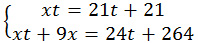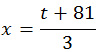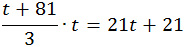Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11) Составим систему уравнений для решения задачи: Решение системы уравнений огэ 21 заданиеРешим ее, раскрыв скобки и преобразовав каждое уравнение: Решение системы уравнений огэ 21 заданиеДалее используем метод вычитания, откуда получим:

Решение системы уравнений огэ 21 заданиеПодставив выражение для x в первое уравнение: Решение системы уравнений огэ 21 заданиеПолучили квадратное уравнение.

t 2 + 81t = 63t + 63

t 2 + 18t – 63 = 0

D = 18 2 — 4·1·(-63) = 324 + 252 = 576

Решение системы уравнений огэ 21 задание

Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит, 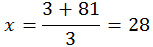Решение системы уравнений огэ 21 заданиеТаким образом, скорость третьего велосипедиста 28 км/ч.Ответ: 28

pазбирался: Даниил Романович | обсудить разбор | оценить

Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно

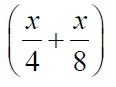
Решение системы уравнений огэ 21 заданиечаса.

Из условия задачи следует, что это время равно 3 часам. Составим уравнение:

Решение системы уравнений огэ 21 задание

Решая уравнение, получаем x = 8.

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:
  1. Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
  2. Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
  3. Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:

В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.

Тогда обозначим искомую массу через Х и составим пропорцию: 4,2 кг – 70% Х – 100%

Решим эту пропорцию:

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:
  1. Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
  2. Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
  3. Решаем систему.
Решение:

Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).

Через каждую из труб должно пройти 200 л воды. Для 1-й трубы получим:

Аналогично для 2-й трубы:

Из уравнения для 2-й трубы выразим t через х:

Подставим полученное для t выражение в уравнение для 1-й трубы: Решение системы уравнений огэ 21 заданиеРешим это уравнение и найдем искомую величину: Решение системы уравнений огэ 21 задание

Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).

Значит, искомая скорость наполнения равна 20 л/мин.

pазбирался: Даниил Романович | обсудить разбор | оценить

Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:

СкоростьВремяРасстояние
1 автомобильх800 х . .800
2 автомобильх – 36800 х − 36 . .800

Пояснения к заполнению таблицы:

Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.

Расстояние у каждого авто будет 800 км.

Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.

Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:

800 х − 36 . . − 800 х . . = 5

Приведем к общему знаменателю х(х-36) наше уравнение и решим его:

800х – 800х+28800=5х 2 – 180

5х 2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:

Решим полученное квадратное уравнение

D=b 2 – 4ac=36 2 – 4 ∙ ( − 5760 ) =24336

х1,2= − b ± √ D 2 a . . = 36 ± 156 2 . .

Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.

Значит, скорость первого автомобиля 36 км/ч

pазбирался: Даниил Романович | обсудить разбор | оценить

💡 Видео

ОГЭ Задание 21 | Сухофрукты | Самое быстрое решение | +2 балла к ОГЭ 2023Скачать

ОГЭ Задание 21 | Сухофрукты | Самое быстрое решение | +2 балла к ОГЭ 2023

Задачи на движение из второй части. Задание 21 | Математика ОГЭ 2023 | УмскулСкачать

Задачи на движение из второй части. Задание 21 | Математика ОГЭ 2023 | Умскул

21 задание ОГЭ математика | Задачи на процентыСкачать

21 задание ОГЭ математика | Задачи на проценты

ОГЭ Задание 21 Системы уравненийСкачать

ОГЭ Задание 21 Системы уравнений

ОГЭ Задание 21 Система уравнений Метод заменыСкачать

ОГЭ Задание 21 Система уравнений Метод замены

ОГЭ Задание 21 Система уравнений Метод заменыСкачать

ОГЭ Задание 21 Система уравнений Метод замены

ОГЭ Задание 21 Система уравненийСкачать

ОГЭ Задание 21 Система уравнений

ОГЭ задание 21 Системы уравнений 3Скачать

ОГЭ задание 21 Системы уравнений 3

ОГЭ Задание 21 Системы уравнений 1Скачать

ОГЭ Задание 21 Системы уравнений 1

ОГЭ Задание 21 Системы уравнений (4)Скачать

ОГЭ Задание 21 Системы уравнений (4)

ОГЭ Задание 21 Система уравнений Разделим первое уравнение системы на второе уравнениеСкачать

ОГЭ Задание 21 Система уравнений Разделим первое уравнение системы на второе уравнение

ОГЭ 21 ЗАДАНИЕ. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ. 3 ВАРИАНТ ЯЩЕНКО 2020Скачать

ОГЭ 21 ЗАДАНИЕ. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ. 3 ВАРИАНТ ЯЩЕНКО 2020

Как решить систему уравнений на ОГЭ 2021? / Полный разбор задачи №20 ОГЭ по математикеСкачать

Как решить систему уравнений на ОГЭ 2021? / Полный разбор задачи №20 ОГЭ по математике

ОГЭ Задание 21 Система уравненийСкачать

ОГЭ Задание 21 Система уравнений

ОГЭ Задание 21 Симметрическая система уравненийСкачать

ОГЭ Задание 21 Симметрическая система уравнений

Задание 21 ОГЭ по математике #16Скачать

Задание 21 ОГЭ по математике #16
Поделиться или сохранить к себе: