Решение системы уравнений над полем вычетов (8 видео)

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 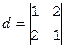, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

В дальнейшем станем действовать аналогично, к тому же не будем педантично ставить индекс +_n, ×_n около символов операций, обозначая их просто + и
× , если значение индекса n ясно из контекста.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре определителя:

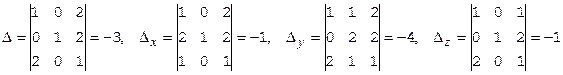
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

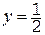
Сделаем проверку (символом Þ обозначен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найденные значения вычетов удовлетворяют системе уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

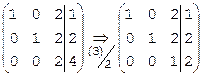
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .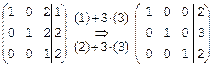

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Помогите с алгеброй. Поле вычетов по модулю

Здесь на сайте как-то кто-то писал решение к вот такой задачке

Решить систему уравнений в поле вычетов по модулю 7.

x + y + z = 1
4x + 2y + 3z = 1
x + 4y + 4z = 2

Вот собственно решение:

Значит, так. Поле вычетов по модулю 7 состоит всего из семи элементов:

При этом противоположные элементы будут выглядеть так:
-1 = 6
-2 = 5
-3 = 4
-4 = 3
-5 = 2
-6 = 1

Обратные элементы, соответственно, будут выглядеть так:
1/2 = 4
1/3 = 5
1/4 = 2
1/5 = 3
1/6 = 6

Разнообразные арифметические аксиомы ассоциативности, коммутативности и дистрибутивности сохраняются в неизменном виде.

Теперь можно решать исходную систему.

Из первого уравнения получаем:
x = 1-y-z = 1+6y+6z
Подставляем это в третье уравнение:
(1+6y+6z) + 4y + 4z = 2
1 + (6+4)y + (6+4)z = 2
1 + 3y + 3z = 2
1 + 3y + 3z + 6 = 2 + 6
3y + 3z = 1
y + z = 5
Подставляем это в первое уравнение:
x + 5 = 1
x + 5 + 2 = 1 + 2
x = 3
Подставляем это во второе уравнение:
4*3 + 2y + 3z = 1
5 + 2(y+z) + z = 1
5 + 2*5 + z = 1
5 + 3 + z = 1
1 + z = 1
z = 0
Тогда y = 5

Получаем ответ: x = 3, y = 5, z = 0

Подскажите пожалуйста, откуда взялось вот это :

Видео:Основы алгебры вычетовСкачать

Алгоритм решения систем линейных уравнений в кольцах вычетов

Алевтина Шахова 6 лет назад Просмотров:

1 Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов [], эквивалентный по сложности известному алгоритму решения систем в полях Галуа ([2], [4]). Приведены результаты сравнительного анализа предложенного алгоритма и существующих аналогов ([3], [0], [8]) на основе асимптотической оценки их временной сложности. Показано, что разработанный метод является корректным и существенно снижает трудоемкость алгоритмов дискретного логарифмирования. Введение Объектом исследования данной работы являются методы решения систем линейных уравнений в кольцах вычетов. Такие системы возникают в алгоритмах факторизации и дискретного логарифмирования (см., например, метод Диксона, алгоритм Копперсмита-Одлыжко-Шреппеля «COS» и алгоритм решета числового поля в [3]). Частным случаем колец вычетов являются поля Галуа, т.е. кольца вычетов по модулю простых чисел. Методы решения систем в таких полях известны (см., например, метод Гаусса (последовательного исключения) в [2, с.89], [4, с.42]). Модификацией метода Гаусса является метод Жордана. Однако для решения систем линейных уравнений в кольцах вычетов эти методы, вообще говоря, неприменимы. Проиллюстрируем сказанное. Рассмотрим систему линейных уравнений: 26x+ 3y = 4 () 9x+ 34y = в поле Галуа Z 37 и в кольце вычетов Z 36. В соответствии с методом Жордана требуется с помощью элементарных преобразований над строками привести матрицу к единичной. Для получения единичного элемента на диагонали в поле действительных чисел используется деление на число a, равное ведущему элементу; аналогом этой операции в кольце вычетов является умножение на элемент, обратный к a. Обратный элемент по модулю можно найти как решение уравнения: ax (mod ) (2) Для его вычисления используется расширенный алгоритм Евклида (см. [7, с. 744], [0, с.227]). На рис. приведено описание этого алгоритма. Если a и — взаимно простые числа, т.е. НОД( a, ) = = ax + y, то 2 ; в противном случае коэффициент Безу x является решением уравнения ( ) уравнение ( ) 2 не имеет решения и элемент a необратим в кольце Z. Как показано в [7, с.743], время работы алгоритма Евклида при вычислении НОД ( ab, ), где a > b 0, составляет O(log b ). Тогда

2 сложность операции вычисления обратного элемента в кольце Z можно оценить как O(log ). Метод Жордана с учетом алгоритма Евклида имеет временную сложность O( n ( n m+ log ) ) для системы n уравнений с m неизвестными в Z. Евклид( ab, ). d x y a 0 n r s b 0 2. c d / n 3. d x y 0 d x y n r s c n r s 4. ЕСЛИ n > 0 5. ТО перейти к шагу 2; 6. ИНАЧЕ вернуть( d, x, y, r, s ) Рис. В результате вычислений, приведенных ниже, получаем решение системы в поле Галуа Z 37 : x = 6, y = 23. [] [] ( 26 = 0 ) 30 3 [2] [] [2] [] 30 3 [2] ( 23 = 29 ) 30 3 [] [2] [2] Однако в кольце вычетов по модулю = 36 система () не может быть решена ни с помощью метода Жордана, ни с помощью метода Гаусса, поскольку все коэффициенты при неизвестных являются делителями нуля ([9, с.75]) и, следовательно, не является обратимыми. Таким образом, получить единичный элемент на диагонали умножением на какой-либо элемент кольца невозможно. Тем не менее, конечность области определения позволяет убедиться в том, что решение данной системы в Z 36 существует ( x = 7, y = 22), и притом единственно. Для решения систем линейных уравнений в кольцах вычетов необходимы специальные методы. Обзор существующих методов Анализ методов решения систем линейных уравнений в кольцах вычетов, описанных в современной литературе, выявил ряд недостатков, которые затрудняют использование этих алгоритмов на практике. В монографии [3] задача сводится к решению систем линейных уравнений над полями Галуа. Пусть

3 где систем t q α = m = ( ) ax b(mod ), i=, n 3 i i =, тогда решение системы ( ) m = 3 сводится к решению семейства ( ) ax b(mod q α ), i=, n, =, t 4 i i где неизвестные значения x (mod q α ) для фиксированного представляются в виде α α x x + x q x q (mod q ), 5 0, α Здесь 0 xl q, l = 0, α. Редуцируя систему ( 4 ) к модулю q, получаем систему уравнений: над полем Галуа виде ( ) q m = 5 с известными i0 поделив на i 0 ax b(mod q), i=, n ( ) Z. Если мы найдем все x,, 0 = m, то, подставляя x в x в систему ( ) 4, редуцируя ее к модулю q, мы получим систему линейных уравнений над полем 2 q и затем относительно неизвестных x,, = m, и т.д. В конечном счете, найдя значение x (mod q α ) для всех, мы восстановим x (mod ) по китайской теореме об остатках (см. [0, с.420]). 2 2 В нашем примере = 36 = 2 3, т.е. для решения одной системы в кольце вычетов придется решить 4 системы над полями Галуа. Но основным недостатком метода является необходимость разложения на множители числа : вопрос о существовании алгоритма факторизации с полиномиальной сложностью является одной из открытых проблем современной теории чисел. Другой метод предполагает сведение системы линейных уравнений в кольце вычетов к системе линейных диофантовых уравнений. При помощи одного из известных алгоритмов (см. [3] или [0]) расширенная матрица системы ( A b ) приводится к ступенчатому виду ( A b ) и вычисляется правая матрица перехода R размером ( m+ ) ( m+ ), такая, что: ( A b) R = ( A b ). На основании матрицы R можно получить общее решение системы. Проиллюстрируем применение данного способа на примере. Система линейных диофантовых уравнений, соответствующая системе ( ) в Z 36, имеет вид: 26x+ 3y+ 36v = 4. 9x+ 34y + 36v2 = Ее общее решение в кольце целых чисел: Z q

4 x = t t (-2492) y = t0 (-324) + t 5688, t0, t Z v = t0 (-857) + t 5048 v2 = 0 + t0 0 + t Редуцируя результат к модулю 36, получаем: x = 7, y = 22. Однако при решении систем линейных уравнений в кольцах вычетов наблюдается экспоненциальный рост длины коэффициентов. Так, в нашем примере коэффициенты исходной матрицы ограничены числом 36, тогда как в 6 целых числах мы получили общее решение с коэффициентами

0. Заметим, что этот результат соответствует системе в кольце вычетов, состоящей всего лишь из двух уравнений с двумя неизвестными. Для того, чтобы избежать экспоненциального роста длины коэффициентов, разработаны специальные методы решения систем линейных алгебраических уравнений над кольцом целых чисел, такие как модификация метода Гаусса и построение нормальной диагональной формы Смита (см. [8, с. 8]). Несмотря на то, что эти алгоритмы являются полиномиальными, их сложность существенно превышает сложность алгоритма Гаусса при решении систем в полях Галуа. Так, для системы из n уравнений с n неизвестными, коэффициенты которой по абсолютной величине не превосходят α, временная сложность модифицированного алгоритма Гаусса при использовании самого быстрого алгоритма умножения составляет O( n 4 (log α + log n ) ). Трудоемкость построения нормальной диагональной формы Смита матрицы 2 O n m 2 logα. A, где a α, i, n,, m n m i = =, ограничена величиной ( ) Метод решения систем линейных уравнений в кольцах вычетов, предлагаемый в данной работе, лишен недостатков вышеописанных алгоритмов и показал свою эффективность при программной реализации. Описание метода В основе разработанного метода лежит преобразование строк матрицы с использованием коэффициентов Безу, которые позволяет вычислить расширенный алгоритм Евклида (см. рис.). В результате работы алгоритма получаем: НОД ( ab, ) = d= a x+ b y, 0 = n = a r+ b s. a = 26 = a, b= 9 = a : НОД (26, 9) = = 26 ( ) + 9 (3), 0= 26 (9) + 9 ( 26). При 2 Применяя к -й и 2-й строке расширенной матрицы системы () преобразования, соответствующие преобразованиям алгоритма Евклида над поступающими на его вход коэффициентами a = 26 и a 2 = 9, в результате мы получаем матрицу, строчно эквивалентную исходной (см. [5, с.27]):

5 [] [] [2] [] [2] 9 34 [2] [] 9 34 [] [2] [] [2] [2] [] [] [2] [] [2] [2] В полученной матрице: A(, ) x y A(, ) = A(2, ) r s A(2, ), где x, y, r, s удовлетворяют условию: НОД ( a, a2) = a x + a2 y, 0 = a r + a2 s (запись A(, ) используется для обозначения -й строки расширенной матрицы A). Коэффициенты Безу x =, y = 3, r = 9, s = 26 можно получить, оперируя лишь коэффициентами a и a 2. Тогда цепь преобразований ( 6 ) сводится к одному преобразованию следующего вида: [] [] =[] 35 + [2] [2] =[] 9 + [2] 0 [2] С учетом того, что коэффициент a 22 = 7 обратим в Z 36 : 7 3(mod36), преобразуем матрицу к единичной и получаем решение: [] [] =[] + [2] [2] =[2] 3 [2] В общем виде алгоритм решения систем линейных уравнений в кольцах вычетов, представляющий собой модификацию метода Жордана, описан на рис.2. Доказательство корректности Предложенный алгоритм является корректным, т.е. полученная в результате преобразований система равносильна исходной (иначе говоря, решения системы не теряются и новые решения не появляются). 3 в матричном виде: Запишем систему уравнений ( ) Ax = b ( 7) Тогда по теореме о равносильности систем линейных уравнений: Если U — обратимая ( n n) коммутативное кольцо с единицей), тогда система уравнений ( ) системе ( UA) x = Ub. (Доказательство см. в [5, с.58]). Следствие из этой теоремы: ( 6) -матрица над R (R — произвольное 7 равносильна Если матрицы ( A, b ) и ( C, δ ) строчно эквивалентны, то система уравнений ( 7 ) равносильна системе Cx = δ.

6 Поскольку преобразования матрицы в описанном модифицированном методе Жордана базируются на элементарных преобразованиях строк (элементарными преобразованиями строк матрицы с элементами из коммутативного кольца с единицей называют (см. [6, с.85]) умножение любой ее строки на обратимый элемент кольца; прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца; транспозицию строк), то полученная на выходе алгоритма матрица строчно эквивалентна исходной (см. Модиф _ Жордан( A ). n Число _ Строк( A) 2. i 3. ДЛЯ = i+, n ЦИКЛ 4. НОД ( aii, ai ) = aii x + ai y ВЫЧИСЛИТЬ x, y, r, s : 0 = aii r + ai s 5. Ai (, ) x y Ai (, ) A(, ) r s A(, ) 6. ЕСЛИ коэффициент a ii необратим в Z 7. ТО выйти из алгоритма 8. ИНАЧЕ 9. A(, i ) A(, i ) a ii 0. A(, ) A(, ) A( i, ) ai, =, i. i i+ 2. ЕСЛИ i n 3. ТО перейти к шагу 2; 4. ИНАЧЕ вернуть( A) [5, с.27]). Тогда приведенному выше следствию соответствующие системы уравнений являются равносильными. Что и требовалось доказать. Оценка сложности Предложенный алгоритм обладает временной сложностью ( ( log )) Рис.2 O n nm+ для системы в кольце вычетов по модулю, в которой n — число уравнений системы, m — число неизвестных. Для получения этой формулы воспользуемся оценкой временной b сложности алгоритма Евклида T( a, b) = O + logϕ НОД ( a, b), где a > b 0, ϕ = ( + 5) 2 (доказательство этой оценки предлагается в [7, с.745], в качестве упражнения). На каждом -м шаге процедура, реализующая алгоритм Евклида, вызывается раз: первым параметром является текущее значение ведущего

7 элемента, в качестве второго на вход последовательно подаются ai ( i = +, n) и. Пусть di — значение ведущего элемента на i -й итерации цикла: d0 = a, d = НОД ( a, a+, ) = НОД ( d0, a+, ). d = НОД ( d, a ). d = НОД ( d, a ). +, n n n, Тогда число операций оценивается неравенством: n min, + log ( n ) + log НОД ( d, a ). i= i i, Помимо этого, на каждом -м шаге над элементами матрицы производится порядка 2( n )( m+ ) 2nm операций. Число шагов алгоритма для системы равно n. Получаем временную сложность алгоритма: n ( ) ( ). Tn (, ) = 2 nm+ ( n ) + log On ( nm+ log ) = Заключение В заключение приведем сравнительный анализ временной сложности предложенного алгоритма и алгоритмов, описанных в современной литературе, для системы n уравнений с m неизвестными в кольце вычетов Z ( t q α = = ). Алгоритм Модифицированный метод Жордана Метод сведения к полям Галуа* Метод сведения к диофантовым уравнениям (с построением матрицы Смита) Временная сложность ( ( + log )) O n nm t O n ( n m α + log ) + ln lnln e = 2 O n m 2 log р ( ) ln ln ln *Оценка временной сложности этого метода дана при условии использования для разложения на множители числа наиболее эффективного на сегодняшний день (см. [7, c.779]) алгоритма «квадратичного решета» () Померанца, имеющего временную сложность L ( ) + o ln ln ln, где L ( ) e =.

8 Список литературы. Авдошин С.М., Савельева А.А. Свидетельство об официальной регистрации программы для ЭВМ : «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ Ван дер Варден Б.Л. Алгебра. — М.: Наука, с. 3. Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, с. 4. Гантмахер Ф.Р. Теория матриц. Гостехиздат, с. 5. Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра: Учебник. В 2-х т. Т. I — М.: Гелиос АРВ, с. 6. Джекобсон Н. Теория колец (Перевод с английского Н. Я. Виленкина). М.: Государственное издательство иностранной литературы, с. 7. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, с. 8. Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. Нижегородский Государственный Университет им. Н.И. Лобачевского. htt:// с. 9. Курош А.Г. Теория групп (Издание третье, дополненное). М.: «НАУКА», Главная редакция физико-математической литературы, с. 0. Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. — М.: Мир, с.