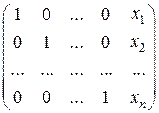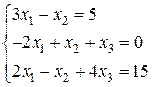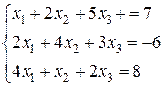Решение системы уравнений методом зейделя в маткаде

Видео:Метод_Зейделя_ExcelСкачать

Последовательность выполнения работы. Решение систем линейных уравнений

Лабораторная работа №4

Решение систем линейных уравнений

Теоретические сведения

Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами.

Методы решения СЛАУ

(4.1)

или в векторном виде

(4.2)

можно разделить на две основные группы: прямые методы и итерационные. Прямые методы дают точное решение за конечное число операций. Итерационные методы дают решение системы уравнений как предел последовательных приближений. Для итерационных методов необходимо выполнение условий сходимости и дополнительных преобразований системы в эквивалентную систему.

Метод матричных преобразований

Пусть требуется найти решение (СЛАУ) вида (4.1).

Введем следующие обозначения:

где – матрица коэффициентов;

– вектор свободных членов;

– вектор неизвестных.

Из линейной алгебры известно, что система (4.2) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.

Применив к уравнению (4.2) аппарат матричных преобразований, получим «матричную» формулу для вычисления :

1. Помножим уравнение (4.2) слева на матрицу, обратную к матрице :

(4.3)

2. Воспользуемся тем свойством, что , где – единична матрица. Тогда уравнение (4.3) примет вид:

(4.4)

3. Воспользуемся тем свойством, что . Тогда уравнение (4.4) примет вид:

(4.5)

где (4.5) – решение системы (4.2).

Метод Жордана-Гаусса

Метод Жордана-Гаусса, или метод последовательных исключений состоит в том, что систему (4.1) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей:

(4.6)

решение которой находят по рекуррентным формулам:

В матричной записи это означает, что сначала элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду (метод Гаусса):

,

а затем эту ступенчатую матрицу преобразуют так, чтобы в первых столбцах получилась единичная матрица (метод Жордана-Гаусса).

Последний, столбец этой матрицы содержит решение системы (4.1).

Метод простых итераций

При решении системы (4.1) методом простой итерации предполагают, что матрица – квадратная и невырожденная.

Предварительно приводят систему (4.2) к итерационному виду:

(4.8) (4.8)

Для произвольного начального вектора итерационный процесс

(4.9)

сходится, если выполнено одно из условий [4.9]

Процесс вычислений заканчивается при выполнении условия

где — одна из метрик, определяемая левой частью (4.10) – (4.12), по которой была установлена сходимость, — заданная точность.

Метод Зейделя.

Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для , он на следующем шаге использует его для отыскания следующего значения . Вычисления ведутся по реккурентной формуле:

Каждое из условий (4.10) – (4.12) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (4.2). Домножая обе части (4.2) на , получим эквивалентную ей систему

где и .

Далее, поделив каждое уравнение на , приведем систему к виду (4.14). Подобное преобразование также гарантирует сходимость итерационного процесса.

Последовательность выполнения работы

Работа с матрицами в пакете Mathcad организована с помощью панели инструментов Matrix (см. рис. 4.1). Кроме этого, система Mathcad представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций .

Рис. 4.1. Назначение некоторых команд,
расположенных на панели инструментов «Matrix»

Задание 1. Найти решение системы линейных уравнений, пользуясь матричными преобразованиями:

Решение. Решение приведено на рис. 4.2.

Рис. 4.2. Решение СЛАУ в пакете MathCAD матричнм способом.

Задание 2.Найти решение системы средствами Mathcad.

Решение. Систему линейных уравнений средствами Mathcad решают:

1) с помощью функции lsolve(A,b) (см. рис. 4.3).

Lsolve(А, b)

Возвращается вектор решения такой, что

– квадратная, не сингулярная матрица.

– вектор, имеющий столько же строк, сколько строк в матрице .

Рис. 4.3. Решение системы уравнений с помощью функции lsolve(A,b).

2) с помощью конструкции Given…Find (см. рис. 4.4). Для этого в рабочий документ нужно записать сужебное слово Given. Далее ниже и правее этого слова записывают левую часть первого уравнения системы и символьный знак равно «Ctrl+=» и правую часть. Аналогично записываются все уравнения системы. Правее и ниже последнего уравнения системы записывается имя функции Find и в скобках перечисляются имена переменных, значения которых необходимо найти. С помощью операции → из панели символьных операций получаем ответ в виде матрицы, каждый столбец которой содержит решение – один из решени системы.

Рис. 4.4. Решение системы уравнений с помощью конструкции Given…Find

Задание 3.Решить СЛАУметодом Жордана-Гаусса.

Решение. Решение приведено на рис. 4.5.

Rref(А)

Возвращается ступенчатая форма матрицы

Augment(А,B)

Возвращается массив, сформированный расположением массивов и «бок о бок». Массивы и должны иметь одинаковое число строк

Submatrix(А,ir,jr,ic,jc)

Возвращается подматрица, состоящая из всех элементов с ir по jr и столбцов с ic по jc. Убедитесь, что ir ≤ jr и ic ≤ jc, иначе порядок строк и (или столбцов) будет обращен.

Рис. 4.5. Решение СЛАУ методом Жордана-Гаусса

Задание 4.Решить СЛАУ методом простой итерации c точностью

Решение. порядок выполнения задания:

1. Введите матрицы 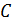и .

2. Преобразуйте исходную систему к виду .

3. Определите нулевое приближение решения.

4. Задайте количество итераций.

5. Вычислите последовательные приближения.

Решение приведено на рис. 4.6.

Рис. 4.6. Решение СЛАУ методом простых итераций

Задание 5.Решить СЛАУ методом Зейделя c точностью

Решение: порядок выполнения задания

1. Введите матрицы и .

2. Преобразуйте исходную систему к виду .

3. Определите нулевое приближение решения.

4. Задайте количество итераций.

5. Вычислите последовательные приближения.

Решение приведено на рис. 4.7.

Рис. 4.7. Решение СЛАУ методом Зейделя

Контрольные вопросы

1. К какому типу – прямому или итерационному – относится метод Жордана-Гаусса?

2. Как организуется контроль над вычислениями в прямом и обратном ходе метода Жордана-Гаусса?

3. Как строится итерационная последовательность для нахождения решения системы линейных уравнений в методе простых итераций?

4. Как формулируется достаточные условия сходимости итерационного процесса в методе простых итераций?

5. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?

Варианты задания к лабораторной работе №4

Задание. Решить СЛАУ следующими методами :

– методом простых итераций;

Найденное решение проверить с помощью встроенных функцй Mathcad. Варианты заданий заданы в табл. 4.1.

Таблица 4.1 – Варианты коэффициентов матриц левой и правой части

Видео:Метод Зейделя Пример РешенияСкачать

Численные методы решения инженерных задач в пакете MathCAD (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

.

Можно применить способ, связанный с вычислением вектора невязки : , показывающий, насколько полученное приближение отличается от точного решения. Затем вычисляется норма вектора невязки . Если она мала, т. е. , то итерационный процесс останавливается.

Рассмотрим несколько способов построения МПИ.

Предположим, что диагональные элементы матрицы A исходной системы (2.1¢) не равны 0 (aii ¹ 0, i = 1, 2, …, n). Разрешим первое уравнение системы (2.1) относительно x1, второе относительно x2 и т. д. Получим систему в виде (2.8):

,

.

Метод, основанный на таком приведении СЛАУ к виду (2.8), называют методом Якоби. Теперь, задав нулевое приближение, по рекуррентным соотношениям (2.9) можем выполнять итерационный процесс. Сформулированное выше условие сходимости в методе Якоби равносильно условию диагонального преобладания:

Действительно, если это условие выполняется, то и суммы модулей элементов строк матрицы a меньше 1.

На рис. 2.2 приведен пример решения в MathCAD методом Якоби системы с матрицей A и вектором правых частей b:

Легко убедиться, что для исходной матрицы A выполняются условия диагонального преобладания, а для матрицы a – условия (2.11), что обеспечивает сходимость итерационного процесса.

Рис. 2.2. Решение СЛАУ

Под методом Зейделя обычно понимается такое видоизменение МПИ (2.10) решения СЛАУ (2.8), в котором для подсчета i-й компоненты (k+1)-го приближения к искомому вектору используются уже вычисленные на этом, т. е. (k+1)-м шаге, новые значения первых i–1 компонент. Это означает, что если система (2.8) тем или иным способом сведена (например, с помощью метода Якоби) к системе (2.9) с матрицей коэффициентов a и вектором свободных членов то ее приближение к решению по методу Зейделя определяется системой равенств

. (2.11)

С точки зрения компьютерной реализации МПИ, использование метода Зейделя означает, что элементы массива будут постепенно замещаться новыми элементами. В связи с такой интерпретацией метод Зейделя иногда называют методом последовательных смещений.

Иногда исходную систему (2.8) не удается привести к виду (2.9), выполняя при этом условие сходимости (2.11). В этом случае можно воспользоваться методом релаксации, который основывается на соотношении , откуда , где t – параметр релаксации. Скалярные формулы метода релаксации имеют следующий вид:

. (2.12)

Раскрыв скобки, можно привести (2.12) к виду (2.10), где коэффициенты матрицы a и вектор свободных членов будут иметь вид: . Подбором параметра t можно добиться сходимости метода релаксации.

2.4. Стандартные функции пакета MathCAD

В MathCAD СЛАУ можно решить как в развернутой форме (2.1), так и в более компактной форме (2.2). Для первого способа следует использовать вычислительный блок Given/Find, состоящий из трех последовательных частей:

– Given – ключевое слово;

– система, записанная логическими операторами в виде равенств и, возможно, неравенств;

– Find(x1, … , xM) – встроенная функция для решения системы относительно переменных x1, … , xM.

Перед вызовом вычислительного блока всем неизвестным присвоены начальные значения. Они могут быть произвольными, т. к. решение СЛАУ с невырожденной матрицей единственно.

Для второй формы записи системы используют встроенную функцию lsolve:

lsolve(A, b) – решение системы линейных уравнений;

A – матрица коэффициентов системы;

b – вектор правых частей.

На рис. 2.3–2.5 приведены примеры решения СЛАУ с помощью стандартных функций MathCAD.

Рис. 2.3. Решение СЛАУ

с помощью вычислительного

Рис. 2.4. Решение СЛАУ
в форме (2.2)

Рис. 2.5. Символьное решение СЛАУ

3. Интерполяция и приближение функций

Слово «интерполяция» в переводе с латыни означает «между точками». Задачи интерполяции часто возникают в инженерных и других практических приложениях. Допустим, что в результате экспериментальных измерений получена таблица значений некоторой функции. Требуется найти промежуточные значения этой функции, а также производные, определяющие скорость ее изменения. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции). Интерполяцию используют для приближенного вычисления интегралов (построение квадратурных формул). Из математического анализа известны, например, многочлены (ряды) Тейлора, которые применяют для вычисления значений гладких (т. е. достаточное число раз дифференцируемых) функций. В точных науках часто используют разложение функций в тригонометрические ряды. Каждый метод имеет свою погрешность, определяемую тем, насколько различаются значения исходной и интерполирующей функций. Существуют ли другие способы интерполяции и приближения функций? Когда и какой способ лучше применять? Какова точность (погрешность) используемых методов интерполяции? Об этом мы узнаем, изучив следующую тему и выполнив соответствующую лабораторную работу.

3.1. Постановка задачи интерполяции

На интервале [a, b] задана система узлов интерполяции
xi, i = 0, 1. N, a £ x i £ b, и значения неизвестной функции в этих узлах fi, i = 0, 1. N. Могут быть поставлены задачи:

1. Найти функцию F(x), принимающую в точках xi заданные значения: F(xi) = fi, i = 0, 1,…, N (условия интерполяции).

Задача имеет много решений: через заданные точки (xi, fi), i = 0, 1. N, можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Если известна исходная функция g(x), то можно оценить погрешность метода в произвольной точке z Î [a, b]: r(z) = |g(z) – F(z)|. Кроме того, можно оценивать равномерную r1 и среднеквадратичную r2 погрешности:

, .

Нас будет интересовать поведение погрешности метода при увеличении числа узлов интерполяции. Будем говорить, что метод сходится, если при N® погрешность r ® 0.

Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале [xi–1, xi] строится своя (локальная) функция. В случае глобальной интерполяции отыскивается одна (глобальная) функция на всем интервале [a, b]. Далее приведены примеры различных способов интерполяции.

Видео:6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

Решение системы линейных алгебраических уравнений

Главная > Решение

Лабораторная работа 3. Решение системы линейных алгебраических уравнений

Цель: Освоить технологию решения систем линейных алгебраических уравнений в интегрированной среде MathCad.

Задание: Решить систему линейных алгебраических уравнений

используя функцию lsolve;

методом простой итерации;

Методика выполнения задания:

Чтобы решить систему линейных алгебраических уравнений можно использовать несколько способов, причем технология нахождения параметров заданной системы линейных алгебраических уравнений на первых этапах аналогична, а именно, пусть задана система трех линейных алгебраических уравнений с тремя неизвестными, найдем ее решение. Для этого присвоим некоторой переменной М матрицу значений коэффициентов при неизвестных, воспользуемся динамической кнопкой , расположенной на панели инструментов Матрица, входящей в Математическую палитру интегрированной среды MathCad. Некоторой переменной V присвоим матрицу – столбец значений, расположенных в правой части системы алгебраических уравнений (то есть после знака =).

Определение решения системы матричным методом .

Используем представление системы линейных алгебраических уравнений в векторной форме, то есть A*X=B, где A – матрица значений при неизвестных, B – вектор свободных членов, а Х – вектор неизвестных, тогда исходя из этого уравнения Х=A -1 *B, задав последнюю формулу получим решение системы линейных алгебраических уравнений.

Видео:9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Определение решения методом Гаусса.

Сформируем расширенную матрицу системы Mr добавлением к матрице М справа матрицу V, используя встроенную функцию augment . Приведем расширенную матрицу к ступенчатому виду Mg, с помощью функции rref и выделим из нее блок матрицы – ее последний столбец, содержащий решение системы, с помощью функции submatrix .

Определение решения системы с помощью встроенной функции lsolve .

Активизируем кнопку Мастер функций на панели инструментов Стандартная и в категории Solving выберем встроенную функцию lsolve (M, V);

Результаты решения заданной системы линейных алгебраических уравнений отображены на рис. ().

l

Рис. Пример решения системы линейных уравнений

4. Решение системы линейных алгебраических уравнений методом простой итераций .

Видео:Решение СЛАУ в пакете MathCadСкачать

Введем переменную ORIGIN = 1 для нумерации столбцов и строк матрицы с 1 (по умолчанию ORIGIN=0). Сформируем матрицы α и β эквивалентной системы х= β + αх.

Для описания i и j воспользуемся кнопкой на панели Калькулятор, для нижних индексов – кнопкой на панели Матрицы.

Определим нормы матрицы α с помощью встроенных функций, используя кнопку на панели инструментов Стандартная.

Зададим начальное приближение, используя кнопку на панели Матрицы.

Вычислим 10 последовательных приближений и погрешности каждого из них.

Фрагмент рабочего документа MathCAD с соответствующими вычислениями приведен ниже на рис ().

Рис. Пример решения системы линейных уравнений методом простой итерации

5. Решение системы линейных уравнений методом Зейделя .

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Сформируем матрицы α и β преобразованной системы х= β + α1х+ α2х и матрицу α= α1+ α2.

Фрагмент рабочего документа MathCAD с соответствующими вычислениями по методу Зейделя приведен ниже на рис ().

Рис. Пример решения системы линейных уравнений методом Зейделя

📸 Видео

Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Метод простой итерации Пример РешенияСкачать

4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать

Неоднородные системы линейных уравненийСкачать

MathCAD Решение системы линейных уравнений матричным методомСкачать

14. Операционное исчисление. Система ДУСкачать

Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Метод наименьших квадратов. ТемаСкачать

2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Mathcad-09. Пример: уравненияСкачать

Метод Гуасса Зейделя, градиентный методСкачать