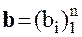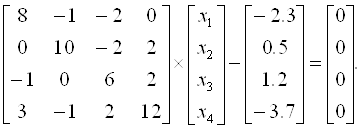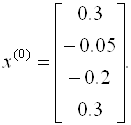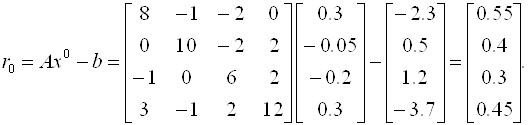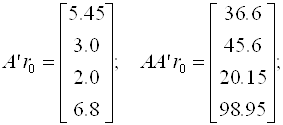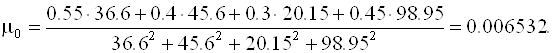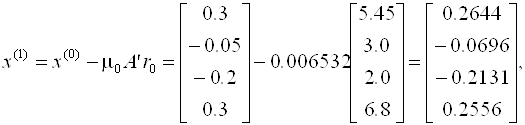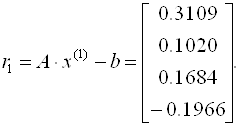Страницы работы
Содержание работы
Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Решить систему линейных алгебраических уравнений (САУ)
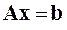
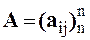
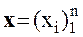
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на 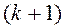
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
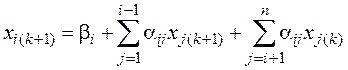
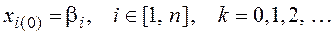
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
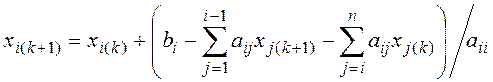
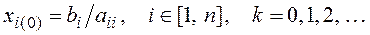
Если матрица 
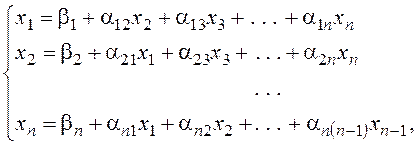
где 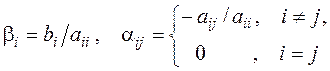


Из неособенной матрицы 

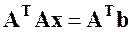
Метод наискорейшего спуска. Данный метод относится к группе нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в которых осуществлялось по отдельным координатам, предполагают траекторию движения к истинному решению сразу по всем координатам по линии наискорейшего спуска в направлении, противоположном вектору градиента функционала, связанного с ошибкой между истинным решением и решением на 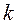
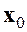
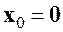
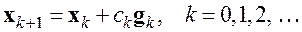
где 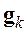
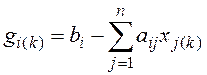
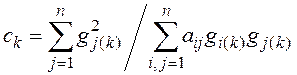
Чтобы упростить процедуру определения вектора невязки, особенно при больших порядках 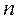
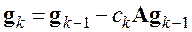
Однако из-за наличия вычислительных погрешностей векторы 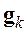
Если матрица 
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) — (N ´ N)-мерная матрица САУ;
B(N) — N-мерный вектор правой части САУ;
N — мерность САУ;
G(N) — N-мерный вектор невязки (g = b — Ax);
X(N) — N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) — N-мерный вектор уточненных значений решения САУ.
Окончание итерационной процедуры производиться при выполнении условия 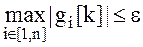
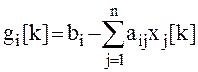
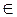
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
Видео:Метод покоординатного спускаСкачать

3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).
Представим систему линейных уравнений в следующем виде:
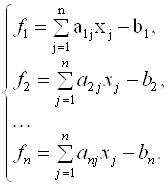
Запишем выражение (3.38) в операторной форме:
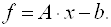
Здесь приняты следующие обозначения:
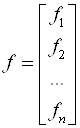
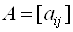

В методе скорейшего спуска решение ищут в виде
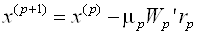
Где 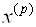
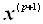
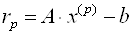
А 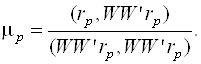
В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:
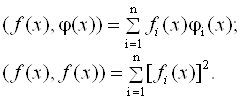
В формуле (3.43) 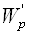

Нетрудно убедиться, что для системы (3.39) матрица Якоби равна

Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять 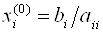
· Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации.
· Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.
· В методе градиента итерационный процесс естественно закончить при достижении 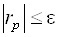
· В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.
· Итерационный процесс можно прервать на любом K–ом шаге и продолжить позднее, введя в качестве нулевого шага значения X(K).
· В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.
Пример 3.7. Методом скорейшего спуска решим систему уравнений
Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:
Следовательно, вектор невязок на нулевом шаге равен
Далее последовательно вычисляем
Отсюда
Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).
Вопросы для самопроверки
· Назовите известные вам методы решения СЛАУ.
· Чем точные методы отличаются от приближенных?
· Что такое прямой и обратный ход в методе Гаусса?
· Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя?
· Что такое невязка?
· Сравните достоинства и недостатки точных и приближенных методов.
· Что такое матрица Якоби?
· Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента?
· Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения
А) начального приближения (нулевой итерации);
Б) первой итерации?
· При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Итерационные методы решения систем линейных алгебраических уравнений
Видео:Решение системы уравнений методом ГауссаСкачать

Стандартные итерационные методы
В разделах Метод исключения Гаусса и Методы решения систем с симметричными матрицами процедуры решения систем алгебраических уравнений были связаны с разложением матрицы коэффициентов ( A ). Методы такого типа называются прямыми методами. Противоположностью прямым методам являются итерационные методы. Эти методы порождают последовательность приближенных решений ( < x^> ). При оценивании качества итерационных методов в центре внимания вопрос от том, как быстро сходятся итерации ( x^ ).
Итерации Якоби и Гаусса — Зейделя
Простейшей итерационной схемой, возможно, являются итерации Якоби. Они определяются для матриц с ненулевыми диагональными элементами. Идею метода можно представить, используя запись ( 3 times 3 )-системы ( Ax = b ) в следующем виде: $$ begin x_1 &= (b_1 — a_x_2 — a_x_3) / a_, \ x_2 &= (b_2 — a_x_1 — a_x_3) / a_, \ x_3 &= (b_3 — a_x_1 — a_x_2) / a_. \ end $$ Предположим, что ( x^ ) — какое-то приближение к ( x = A^b ). Чтобы получить новое приближение ( x^ ), естественно взять: $$ begin x_1^ &= (b_1 — a_x_2^ — a_x_3^) / a_, \ x_2^ &= (b_2 — a_x_1^ — a_x_3^) / a_, \ x_3^ &= (b_3 — a_x_1^ — a_x_2^) / a_. \ end $$
Эти формулы и определяют итерации Якоби в случае ( n = 3 ). Для произвольных ( n ) мы имеем $$ begin tag x_i^ = left( b_i — sum_^ a_x_j^ — sum_^ a_x_j^ right)/a_, quad i = 1, 2, ldots, n. end $$
Заметим, что в итерациях Якоби при вычислении ( x_i^ ) не используется информация, полученная в самый последний момент. Например, при вычислении ( x_2^ ) используется ( x_1^ ), хотя уже известна компонента ( x_1^ ). Если мы пересмотрим итерации Якоби с тем, чтобы всегда использовать самые последние оценки для ( x_i ), то получим: $$ begin tag x_i^ = left( b_i — sum_^ a_x_j^ — sum_^ a_x_j^ right)/a_, quad i = 1, 2, ldots, n. end $$ Так определяется то, что называется итерациями Гаусса — Зейделя.
Для итераций Якоби и Гаусса — Зейделя переход от ( x^ ) к ( x^ ) в сжатой форме описывается в терминах матриц ( L, D ) и ( U ), определяемых следующим образом: $$ begin L &= begin 0 & 0 &cdots & cdots & 0 \ a_ & 0 &cdots & cdots & 0 \ a_ & a_ & 0 & cdots & 0 \ vdots & vdots & vdots & ddots &vdots\ a_ & a_ & cdots & a_ & 0 end, \ D &= mathrm(a_, a_, ldots, a_), \ U &= begin 0 & a_ &a_ & cdots & a_ \ 0 & 0 & a_ & cdots & a_ \ vdots & vdots & ddots & ddots &vdots\ 0 & 0 & cdots & 0 & a_ \ 0 & 0 & cdots & 0 & 0 end. end $$ Шаг Якоби имеет вид ( M_J x^ = N_J x^ + b ), где ( M_J = D ) и ( N_J = -(L+U) ). С другой стороны, шаг Гаусса — Зейделя определяется как ( M_G x^ = N_G x^ + b ), где ( M_G = (D+L) ) и ( N_G = -U ).
Процедуры Якоби и Гаусса — Зейделя — это типичные представители большого семейства итерационных методов, имеющих вид $$ begin tag M x^ = N x^ + b, end $$ где ( A = M-N ) — расщепление матрицы ( A ). Для практического применения итераций (9) должна «легко» решаться система с матрицей ( M ). Заметим, что для итераций Якоби и Гаусса — Зейделя матрица ( M ) соответственно диагональная и нижняя треугольная.
Сходятся ли итерации (9) к ( x = A^b ), зависит от собственных значений матрицы ( M^N ). Определим спектральный радиус произвольной ( n times n )-матрицы ( G ) как $$ rho(G) = max , $$ тогда если матрица ( M ) невырожденная и ( rho(M^N) —>
🎥 Видео
Решение систем уравнений методом подстановкиСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение систем уравнений методом сложенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Система с тремя переменнымиСкачать

Градиентный метод | метод скорейшего спуска + примерСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение систем уравнений методом сложенияСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы уравнений методом Гаусса 4x4Скачать

ЦОС Python #2: Метод градиентного спускаСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать