Решение системы уравнений методом простой итерации в mathcad (3 видео)

Метод простых итераций

Дата добавления: 2015-07-23 ; просмотров: 7484 ; Нарушение авторских прав

Лабораторная работа №5

Тема: Решение СЛАУ итерационным методом в MathCAD.

Цель: изучение приемов численного решения систем линейных уравнений с помощью функций MathCAD.

Порядок выполнения работы

1. Ознакомиться с теоретическими положениями.

2. Рассмотреть пример решения СЛАУ итерационным методом в MathCAD.

3. Выполнить практическое задание.

4. Ответить на контрольные вопросы.

Содержание отчета

1. Тема, цель работы.

2. Практическое задание:

2.1. Постановка задачи.

2.2. Результаты выполнения.

3. Ответы на контрольные вопросы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Итерационные методы – это методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.

Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

Метод простых итераций

Пусть дана линейная система (1).

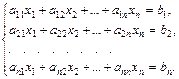Решение системы уравнений методом простой итерации в mathcad

(1)

Систему (1) коротко можно записать в виде матричного уравнения:

Ах = b,

(2)

Предполагая, что диагональные коэффициенты

разрешим первое уравнение системы (1) относительно х₁, второе – относительно х₂ и т. д. Тогда получим эквивалентную систему

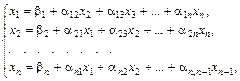(3)

при i ¹ j

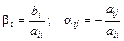
Систему (3) можно записать в матричной форме

x = b + ax,

а любое (k + 1) приближение вычисляется по формуле

x (k+1) = b + ax (k) .

(4)

Напишем формулы приближений в развернутом виде:

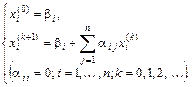(4¢)

Приведем достаточное условие сходимости метода итераций.

Теорема:Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть

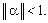(5)

Следствие 1. Процесс итерации для системы (3) сходится, если:

1) (k +1) .

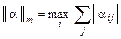
Пример решения СЛАУ итерационным методом в MathCAD.

Решить систему методом простых итераций:

Результат на экране:

Видео:Метод простой итерации Пример РешенияСкачать

MathCAD — это просто! Часть 4. Системы линейных алгебраических уравнений

Итак, мы с вами продолжаем изучать MathCAD — самую дружелюбную к пользователю математическую среду из существующих в настоящее время. Пока мы занимались тем, что изучали способы решения уравнений — трансцендентных и алгебраических, и теперь вы знаете, как их решать с помощью MathCAD’а в общем виде или численно. Как вы могли убедиться из материала третьей части, численное решение уравнений — не такая простая задача, как может показаться с первого взгляда, однако и не такая сложная, если построить график уравнения. Но просто уравнения — это, согласитесь, довольно скучно, потому что в жизни, как правило, уравнения по одиночке не встречаются. Поэтому сегодня мы перейдем к более сложной, а значит, и более интересной, теме — попробуем решать системы уравнений. Я сказал «попробуем»? Простите, пожалуйста — я, наверное, оговорился. Конечно, не попробуем, а научимся — потому что благодаря MathCAD’у можно быть уверенным в том, что подобные попытки увенчаются успехом. Готовы? Ну что же, тогда вперед.

Решение систем с помощью функции lsolve

Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.

Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0
k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0

Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0

Здесь K — матрица (kij), составленная из коэффициентов при переменных величинах, где i — номер строки матрицы, а j — номер столбца. X и L — это, соответственно, векторы, составленные из переменных и свободных членов. Собственно, при решении СЛАУ с помощью MathCAD мы будем записывать СЛАУ именно в таком виде, потому что решение СЛАУ в MathCAD реализовано именно с помощью матричных методов. Возможно, вы что-нибудь слышали о методах решения СЛАУ Гаусса и Крамера, но даже если и нет, ничего страшного в этом нет — MathCAD тем и удобен, что с его помощью можно решать уравнения, не задумываясь над тем, каким именно алгоритмом пользуется математическая система при их решении.

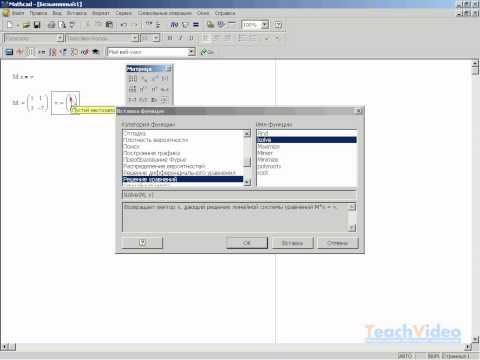
Итак, для начала давайте посмотрим, каким именно образом в MathCAD’е нужно задавать матрицы. Для этого на панели инструментов Matrix нажмите кнопку Matrix or Vector, а в появившемся окне задайте количество столбцов и строк в матрице. Мы с вами попробуем решать для начала СЛАУ из четырех уравнений, и, соответственно, нам нужна будет матрица размером четыре на четыре элемента. Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать «K_:=», а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете
воспользоваться теми, которые приведены на скриншоте — с ними цифры в ответе получаются довольно ровными и красивыми), нужно для решения СЛАУ использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать:
lsolve(K_, L_) =

Ну, а после знака равенства MathCAD нам уже нарисует результат.

С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, «а». Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак «равно» в MathCAD’е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.

Решение с помощью solve

В общем-то, решать такую систему можно было бы и используя уже знакомый нам с вами оператор solve. Для этого достаточно записать уравнения в виде матрицы, а затем применить к ней оператор solve точно так же, как если бы мы с вами решали не целую систему, а всего лишь одно- единственное уравнение. «Записать уравнения в виде матрицы» в данном случае означает не запись матричного уравнения KX + L = 0, а просто запись в каждой строке одностолбцовой матрицы (т.е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу «=», а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.

Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи. Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.

Численное решение СЛАУ

Что ж, давайте теперь посмотрим, как решать СЛАУ с использованием численных методов их решения. Это тоже вовсе не так сложно, как может с самого начала показаться, поскольку MathCAD имеет в своем арсенале ряд средств и на этот случай. Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово «Given» (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово «Given» и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.

Теперь, когда вы знаете уже столько разных способов решения СЛАУ, вполне логично было бы задаться вопросом: а какой из них лучше при прочих равных условиях? В литературе, как правило, рекомендуется использовать функции lsolve или find, дающие точность до 15 знаков после запятой — однако на самом деле, учитывая тот факт, что такая точность бывает нужна не так уж часто, данным советом можно пренебречь, потому что точность решения системы намного больше зависит от нее самой, нежели от используемого метода ее решения в MathCAD’е. Так что используйте пока что смело тот, который показался вам наиболее удобным, а о погрешностях при решении СЛАУ мы с вами еще поговорим, но только, пожалуй, немного попозже.

Компьютерная газета. Статья была опубликована в номере 16 за 2008 год в рубрике soft

Видео:Решение СЛАУ в пакете MathCadСкачать

Численные методы решения инженерных задач в пакете MathCAD (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Рис. 2.1. Решение СЛАУ методом обратной матрицы

Наиболее известным и популярным точным способом решения линейных систем вида (2.1) является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке.

Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

Из нее в обратном порядке находим все значения xi:

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие-либо ведущие элементы малы, то это приводит к увеличению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

, i, j = 1, 2, …, m,

т. е. осуществляется выбор первого главного элемента. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т. д.

Часто возникает необходимость в решении СЛАУ, матрицы которых являются слабо заполненными, т. е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы.

Рассмотрим наиболее простой случай: систему с трехдиагональной матрицей коэффициентов, к которой сводится решение ряда численных задач (сплайн-интерполяция таблично заданной функции, дискретизация краевых задач для дифференциальных уравнений методами конечных разностей и др.). Тогда СЛАУ можно записать в упрощенном виде:

, (2.2)

где i = 1, 2, …, m. Схема (2.2) имеет трехдиагональную структуру, что хорошо видно из следующего, эквивалентного (2.2), векторно-матричного представления:

Если при этом выполняется условие , то говорят, что матрица этой системы имеет диагональное преобладание.

Предположим, что существуют такие наборы чисел ai и bi
(i = 1, 2, …, m–1), при которых

. (2.3)

Уменьшим в (2.3) индекс на единицу:
и подставим полученное выражение в (2.2)

откуда . Данное равенство в точности совпадает с (2.3), если при всех i = 1, 2, …, m–1 выполняются рекуррентные соотношения

, . (2.4)

Процесс вычисления ai и bi можно начать со значений

, . (2.4¢)

Далее продолжаем по формулам (2.4) последовательно при
i = 1, 2, …, m–1. При i = m из (2.2) имеем

. (2.5)

В то же время при i = m–1 из (2.3) получаем

. (2.6)

Подставляя выражение для xm–1 из (2.6) в (2.5) и решая полученное выражение относительно xm, получаем:

, (2.7)

где am и bm известны из предыдущего шага. Далее по формулам (2.3) последовательно находятся xm–1, xm–2, …, x1.

Данный способ решения системы уравнений вида (2.2) называется методом прогонки. Исходя из вышеизложенного, можно выделить три этапа метода прогонки. На первом этапе по формулам (2.4¢), (2.4) определяются так называемые прогоночные коэффициенты ai и bi при i = 2, 3, …, m (прямая прогонка). Затем по формуле (2.7) находится xm. На последнем этапе по формуле (2.3) определяются xi при i = m–1, m–2, …, 1 (обратная прогонка).

Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при больших размерностях систем не должно быть быстрого роста погрешностей округления.