Содержание:
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Решение систем линейных уравнений
- Решение СЛАУ
- Методы Гаусса и Крамера
- Действия над матрицами. Матричный способ решения СЛАУ
- 💥 Видео
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Решение системы уравнений методом Крамера.Скачать

Решение систем линейных уравнений
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
Видео:10. Метод Крамера решения систем линейных уравнений.Скачать

Решение СЛАУ
Содержание:
Определители, их свойства
Квадратной матрицей n-го порядка называется таблица чисел
Числа 


Определителем (детерминантом) II порядка, соответствующим квадратной матрице II порядка, называется число, обозначаемое символом 
Определителем III порядка, соответствующим квадратной матрице III порядка, называется число, вычисляемое по правилу 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры №1:
Минором 





Например, для определителя III порядка (1.1)
Свойства определителей следуют из определения (1.1).
1°. Транспонирование: определитель не изменится, если все его строки заменить на соответствующие столбцы:
2°. Разложение определителя по любому ряду (строке или столбцу):
определитель равен сумме произведения элементов любого ряда на их алгебраические дополнения. Например, для определителя (1.1) разложение по второму столбцу:
3°. Перестановка двух строк (столбцов) определителя равносильна умножению его на (-1).
4°. Определитель
1) все элементы какого-нибудь ряда равны нулю;
2) соответствующие элементы двух строк (столбцов) пропорциональны (в частности, равны).
5°. Общий множитель всех элементов ряда можно вынести за знак определителя. 6°. Определитель не изменится, если к элементам одной его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Возможно вам будут полезны данные страницы:
Аналогично определению определителя III порядка вводится определение определителя
n-го порядка, соответствующего квадратной матрице n-го порядка.
Например, определителем IV порядка называется число, вычисляемое по правилу
Свойства 1°—6° сохраняются для определителей любого порядка. При вычислении определителей IV и выше порядков удобно, используя свойство 6°, преобразовать его так, чтобы все элементы (кроме одного) какого-нибудь ряда были нулями, затем разложить его по этому ряду.
Пример 1:
Здесь вторую строку последовательно умножаем на 2, 3, 5 и складываем соответственно с 1-й, 3-й, 4-й строками. Системы линейных алгебраических уравнений их совместность, определенность.
Методы Гаусса и Крамера
Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными будем называть следующую систему:
где 






СЛАУ называется совместной, если она имеет решение, несовместной — если решения нет.
Однородная система всегда совместна, так как имеет нулевое решение.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений бесконечное множество.
Две совместные системы называются равносильными, если все их решения совпадают.
Система (1.2) переходит в равносильную, если:
- а) поменять местами два уравнения;
- б) умножить любое уравнение на число
- в) прибавить к обеим частям одного уравнения соответствующие части другого, умноженные на любое число.
Назовем такие преобразования системы элементарными. Коэффициенты при неизвестных в системе составляют прямоугольную таблицу — матрицу из m строк и n столбцов:
Она называется основной матрицей системы, а матрица 
Преобразования со строками расширенной матрицы системы, соответствующие элементарным преобразованиям системы, будем тоже называть элементарными, а матрицы, полученные при элементарных преобразованиях, — эквивалентными.
Обозначим i-ю строку матрицы А через
Строки 


Рангом матрицы А (обозначается rang А) называется максимальное число линейно независимых строк матрицы. Ранг матрицы не меняется при элементарных преобразованиях.
Т: (Кронекера—Капелл и) Система (1.2) совместна тогда, когда rang А = rang (A | В) Доказательство см. в [1. С.97]. Для решения системы (1.2) применяется метод Гаусса — метод последовательного исключения неизвестных из уравнений системы путем элементарных преобразований.
Все преобразования проводятся с расширенной матрицей. Пусть 




Возможны три случая:
1) Получилась строка 


2) Число ненулевых строк г меньше числа неизвестных, тогда система имеет бесчисленное множество решений. Последней ненулевой строке соответствует уравнение
из которого находим неизвестное хг через и — г так называемых свободных неизвестных: 

3) Если 


Пример 2:

Второй строке соответствует уравнение 






При 




Выведем формулы Крамера, например, для системы трех уравнений с тремя неизвестными. Для этого умножаем 1-е, 2-е и 3-е уравнения системы соответственно на алгебраические дополнения 







Пример 3:


Действия над матрицами. Матричный способ решения СЛАУ
Матрица (1.3) кратко записывается в виде 




Сложение матриц. Суммой матриц 


Сложение матриц подчиняется переместительному и сочетательному законам:
Матрица, все элементы которой нули, называется нуль-матри-цей, обозначается 0;
Умножение матрицы на число.
Произведением матрицы А на число 
Умножение матриц. Произведением матрицы 



Произведение матриц в общем случае не подчиняется переместительному закону:
Сочетательный и распределительный законы справедливы:
Примеры №2:


Если матрица С — АВ для квадратных матриц А и В, то 
Матрица 


Доказательство см. в [1. С.76]. В процессе доказательства получен вид матрицы 



Пример 3:









Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
💥 Видео
Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Решение системы трех уравнений по формулам КрамераСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Решение системы уравнений методом Крамера 4x4Скачать

2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать

Решение СЛАУ методом Крамера. Линейная алгебраСкачать

Линейная алгебра, 8 урок, Метод КрамераСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать







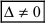 ), то система имеет единственное решение;
), то система имеет единственное решение;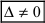 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 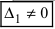 или
или 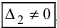 , или, . или
, или, . или 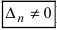 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);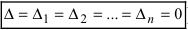 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.














































