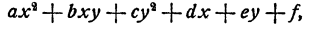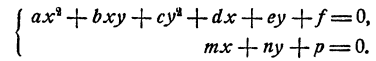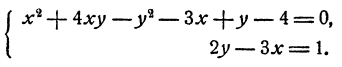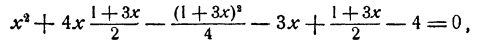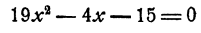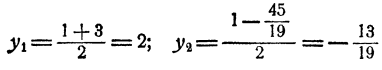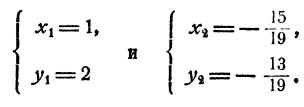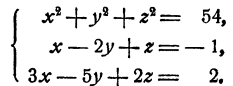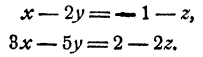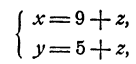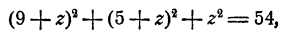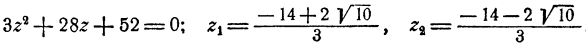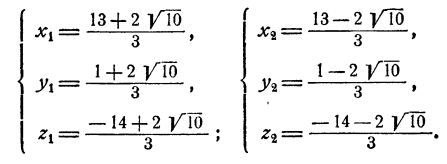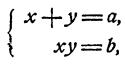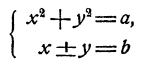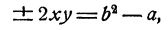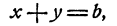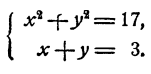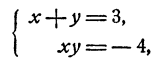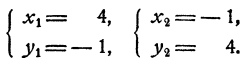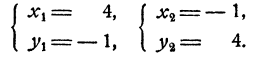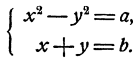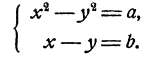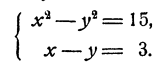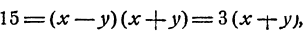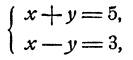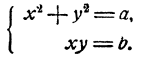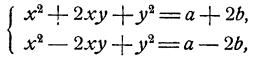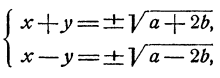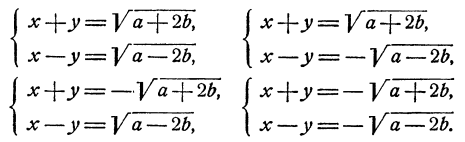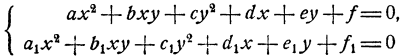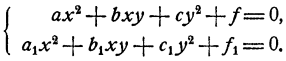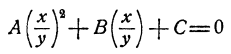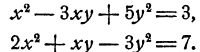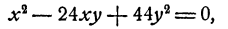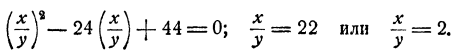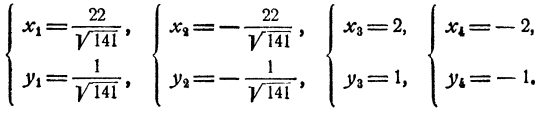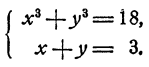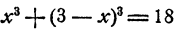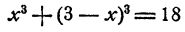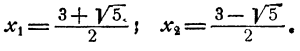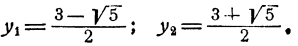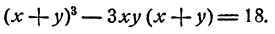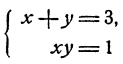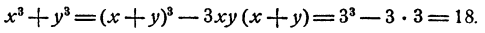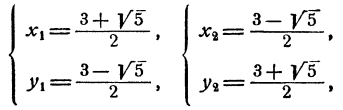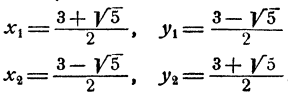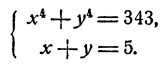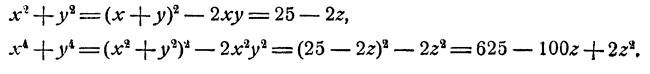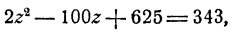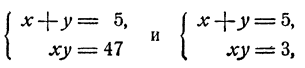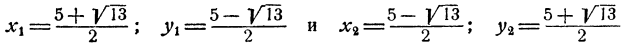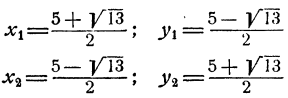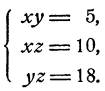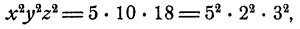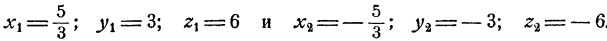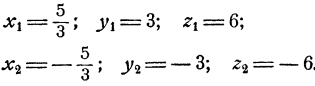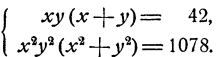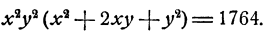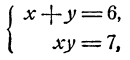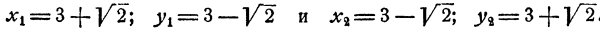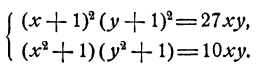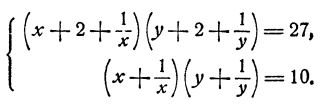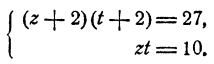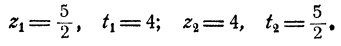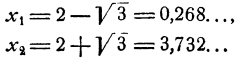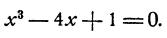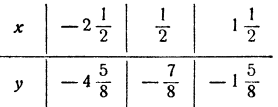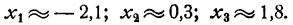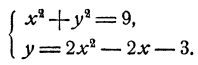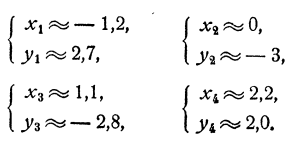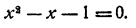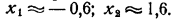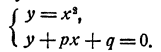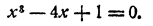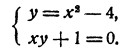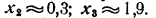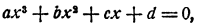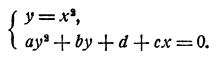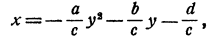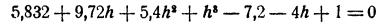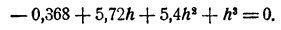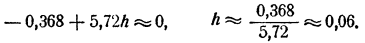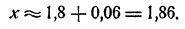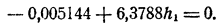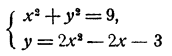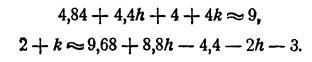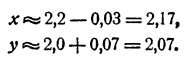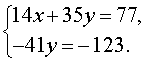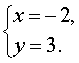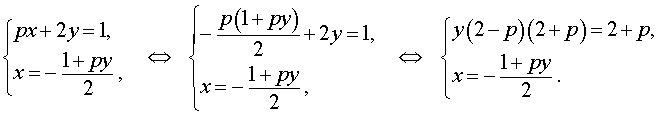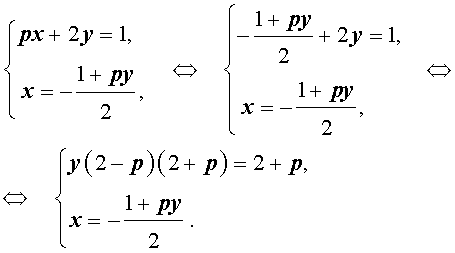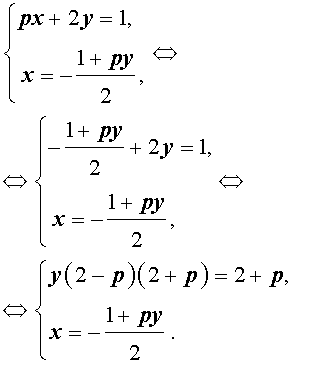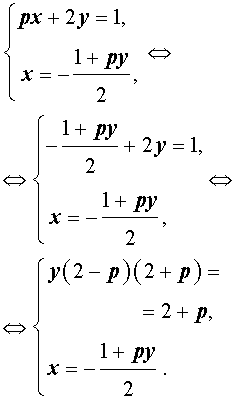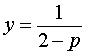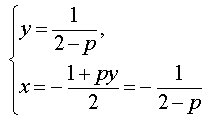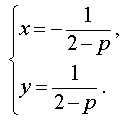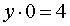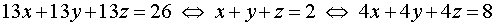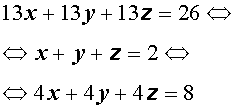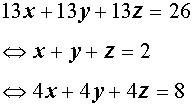- Система уравнений второй степени. Способы решения
- Системы уравнений высших степеней в математике с примерами решения и образцами выполнения
- Системы уравнений, решаемые особыми приемами
- Системы двух уравнений второй степени, не содержащие линейных членов
- Решение систем уравнений высших степеней
- Графическое решение уравнений с одним неизвестным
- Графическое решение систем двух уравнений с двумя неизвестными
- Уточнение корня уравнения или решения системы нелинейных уравнений, исходя из грубого приближения
- Системы линейных уравнений
- Линейные уравнения (уравнения первой степени) с двумя неизвестными
- Системы из двух линейных уравнений с двумя неизвестными
- Системы из трех линейных уравнений с тремя неизвестными
- 📺 Видео
Система уравнений второй степени. Способы решения
Система уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени.
Систему из двух уравнений, в которой одно уравнение второй степени, а второе уравнение первой степени, решают следующим образом:
1) в уравнении первой степени одну переменную выражают через другую;
2) подставляют полученное выражение в уравнение второй степени, благодаря чему получается уравнение с одной переменной;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующие значения второй переменной.
Пример : Решим систему уравнений
1) Второе уравнение является уравнением первой степени. В ней выражаем переменную x через y:
2) в первом уравнении вместо x подставляем полученное выражение 1 – 2y:
Раскрываем скобки и упрощаем:
Приравниваем уравнение к нулю и решаем получившееся квадратное уравнение:
3) Решив квадратное уравнение, найдем его корни:
4) Осталось найти значения x. Для этого в одно из двух уравнений системы просто подставляем значение y. Второе уравнение проще, поэтому выберем его.
Итак, подставляем значения y в уравнение x + 2y = 1 и получаем:
1) х + 2(-0,125) = 1
х – 0,25 = 1
х = 1 + 0,25
х1 = 1,25.
Способы решения системы уравнений с двумя уравнениями второй степени.
1. Замена системы уравнений равносильной совокупностью двух систем.
Пример : Решим систему уравнений
Здесь нет уравнений первой степени, поэтому решать их вроде бы сложнее. Но в первом уравнении многочлен можно разложить на линейные множители и применить метод группировки:
(Пояснение-напоминание: x – 3y встречается в выражении дважды и является общим множителем в многочлене (x – 3y)(x + 3y) – 1(x – 3y). По правилу группировки, мы умножили его на сумму вторых множителей и получили равносильное уравнение).
В результате наша система уравнений обретает иной вид:
Первое уравнение равно нулю только в том случае, если x – 3y = 0 или x + 3y – 1 = 0.
Значит, нашу систему уравнений мы можем записать в виде двух систем следующего вида:
Мы получили две системы, где первые уравнения являются уравнениями первой степени. Мы уже можем легко решить их. Понятно, что решив их и объединив затем множество решений этих двух систем, мы получим множество решений исходной системы. Говоря иначе, данная система равносильна совокупности двух систем уравнений.
Итак, решаем эти две системы уравнений. Очевидно, что здесь мы применим метод подстановки, подробно изложенный в предыдущем разделе.
Обратимся сначала к первой системе.
В уравнении первой степени выразим х через у:
Подставим это значение во второе уравнение и преобразим его в квадратное уравнение:
Как решается квадратное – см.раздел «Квадратное уравнение». Здесь мы сразу напишем ответ:
Теперь подставим полученные значения у в первое уравнение первой системы и решим его:
Итак, у нас есть первые ответы:
Переходим ко второй системе. Не будем производить вычисления – их порядок точно такой же, что и в случае с уравнениями первой системы. Поэтому сразу напишем результаты вычислений:
Таким образом, исходная система уравнений решена.
1 1
(–3 — ; –1 — ), (3; 1), (2,5; –0,5), (–2; 1).
2 6
2. Решение способом сложения.
Пример 2 : Решим систему уравнений
Второе уравнение умножим на 3:
Зачем мы умножили уравнение на 3? Благодаря этому мы получили равносильное уравнение с числом -3y, которое встречается и в первом уравнении, но с противоположным знаком. Это поможет нам буквально при следующем шаге получить упрощенное уравнение (они будут взаимно сокращены).
Сложим почленно левые и правые части первого уравнения системы и нашего нового уравнения:
Сводим подобные члены и получаем уравнение следующего вида:
Упростим уравнение еще, для этого сокращаем обе части уравнения на 5 и получаем:
Приравняем уравнение к нулю:
Это уравнение можно представить в виде x(x – 2y) = 0.
Здесь мы получаем ситуацию, с которой уже сталкивались в предыдущем примере: уравнение верно только в том случае, если x = 0 или x – 2y = 0.
Значит, исходную систему опять-таки можно заменить равносильной ей совокупностью двух систем:
Обратите внимание: во второй системе уравнение x – 2y = 0 мы преобразовали в x = 2y.
Итак, в первой системе мы уже знаем значение x. Это ноль. То есть x1 = 0. Легко вычислить и значение y: это тоже ноль. Таким образом, первая система имеет единственное решение: (0; 0).
Решив вторую систему, мы увидим, что она имеет два решения: (0; 0) и (–1; –0,5).
Таким образом, исходная система имеет следующие решения: (0; 0) и (–1; –0,5).
3. Решение методом подстановки.
Этот метод был применен в начале раздела. Здесь мы выделяем его в качестве одного из способов решения. Приведем еще один пример.
Пример . Решить систему уравнений
│х + у = 9
│у 2 + х = 29
Первое уравнение проще, поэтому выразим в нем х через у:
Теперь произведем подстановку. Подставим это значение х во второе уравнение, получим квадратное уравнение и решим его:
у 2 + 9 – у = 29
у 2 – у – 20 = 0
D = b 2 – 4ас = 1 – 4 · 1 · (–20) = 81
Осталось найти значения х. Первое уравнение проще, поэтому им и воспользуемся:
1) х + 5 = 9
х = 9 – 5
х1 = 4
2) х – 4 = 9
х = 9 + 4
х2 = 13
Видео:Решение систем уравнений второй степениСкачать

Системы уравнений высших степеней в математике с примерами решения и образцами выполнения
Системы двух уравнений первой и второй степени с двумя неизвестными:
Общий вид многочлена второй степени от двух переменных у и x, очевидно, следующий:
где а, b, с, d, е, f—данные числа. Общий вид системы уравнений с двумя неизвестными, состоящей из одного уравнения первой степени и одного уравнения второй степени, следующий:
Система такого вида легко решается способом подстановки. Именно, из второго уравнения можно выразить одно из неизвестных через другое и затем подставить в первое уравнение. В результате этого первое уравнение превратится в уравнение с одним неизвестным, вообще говоря, квадратное. Решив это уравнение, мы сможем определить затем и значения нового неизвестного.
При этом способе решения систем проверка полученных решений посредством подстановки в уравнение системы не обязательна и производится только для контроля правильности вычислений, ибо можно доказать, что при исключении одного неизвестного указанным способом лишних решений возникнуть не может.
Пример:
Решение:
Исключим из системы неизвестное у. С этой целью решим второе уравнение относительно у. Получим 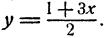
откуда после преобразований
и, следовательно, 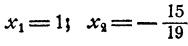
Ответ. Система имеет два решения
Тот же прием исключения следует применять при решении систем трех уравнений с тремя неизвестными, если два уравнения имеют первую степень, третье квадратное. При этом из двух уравнений первой степени нужно выразить два неизвестных через третье неизвестное, и полученные выражения подставить в уравнение второй степени.
Таким же образом можно поступать при решении систем я уравнений с п неизвестными при любом я, если все уравнения, кроме одного квадратного, имеют первую степень.
Пример:
Решение:
Перепишем два последних уравнения системы в виде
Решая эту систему относительно х и у по обычным правилам, получим
Подставив эти выражения в первое уравнение, получим
Остается определить соответствующие значения для х и у, что делается подстановкой значений z₁, и z₂ в выражении х и у через z. Мы получим два решения системы:
Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Системы уравнений, решаемые особыми приемами
В гл. II, § 9 мы рассматривали системы уравнений вида
которые легко решаются при помощи формул Виета. Но, конечно, можно решать такие системы и способом исключения, описанным в предыдущем параграфе.
Часто встречающиеся системы уравнений вида
легко решаются методом исключения, но их можно решать и иначе. Именно, возведя в квадрат второе уравнение и вычитая из него первое, мы получим новое уравнение
которое является следствием данной системы. Объединив его с уравнением
мы получим систему, решаемую при помощи формул Виета.
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то 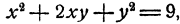
для которой получаем два решения
Оба они удовлетворяют уравнениям исходной системы.
Еще проще решаются системы вида
Действительно, х² — y² = (x — у)(х + у), и потому если допустить, что х и у удовлетворяют обоим уравнениям системы, то (х—у) b = а, и следовательно, 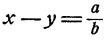
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то
и следовательно, х + у =b. Решая систему
получим х = 4; v = 1.
Ответ. х = 4; v = 1.
Наконец отметим системы вида
Такие системы уравнений можно решить способом исключения, именно, в силу второго уравнения 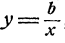
Однако здесь следует рекомендовать другой прием. Именно, если к первому уравнению добавить, а затем вычесть удвоенное второе, то мы получим новую систему
являющуюся следствием исходной.
Но новая система легко решается, ибо из нее следует, что
и система распадается на 4 системы уравнений первой степени
Следует отметить, что сопоставление результатов решения рассмотренной системы по способу исключения и при помощи указанного искусственного приема приводит к тем же соотношениям, которые были получены из сопоставления двух способов решения биквадратного уравнения.
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Системы двух уравнений второй степени, не содержащие линейных членов
Решение системы двух уравнений второй степени с двумя неизвестными общего вида
представляет значительные трудности. Именно, можно доказать, что решение такой системы зачастую сводится к решению уравнения четвертой степени, а нахождение решения общего уравнения четвертой степени представляет довольно сложную задачу, не входящую в рамки курса элементарной алгебры.
Для некоторых систем частного вида возможно элементарное решение. Важным примером таких систем являются системы двух квадратных уравнений, каждое из которых не содержит членов первой степени относительно неизвестных, т. е. системы вида
В этом случае система решается посредством уничтожения свободных членов. Это делается так. Первое уравнение умножается на f₁ второе на f и полученные уравнения вычитаются. Составленное так новое уравнение является следствием исходной системы и имеет вид Ах²+Вху+Су² =0, из которого следует, что
(если только у ≠ 0), откуда мы можем определить отношение
Найдя это отношение, мы можем выразить х через у и затем подставить в одно из уравнений исходной системы. Получившееся в результате неполное квадратное уравнение относительно у легко решается.
Нетрудно видеть, что если А ≠ 0 и хотя бы один из свободных членов в исходных уравнениях отличен от 0, то сделанное выше предположение у ≠ 0 не нарушает общности.
Действительно, если в уравнении Ах² + Вху + Су² == 0 при А ≠ 0 положим у = 0, то и х = 0. Но x = 0; y = 0 не может быть решением исходной системы, если хотя бы один из ее свободных членов отличен от нуля.
Если же коэффициент А = 0, то решение вспомогательного уравнения Вху + Су² = 0 только упрощается, для решения достаточно вынести за скобку у и приравнять к нулю каждый множитель.
Пример:
Решение:
Умножив первое уравнение на 7 и второе на 3, получим после вычитания
Таким образом, х = 22у или х = 2у. Дальнейшее очевидно. Доведя решение до конца, получим четыре решения системы
Видео:Решение систем уравнений второй степени | Алгебра 9 класс #19 | ИнфоурокСкачать

Решение систем уравнений высших степеней
Задача о решении системы уравнений высших степеней с несколькими неизвестными в общем случае является очень трудной, часто не допускающей решения средствами элементарной алгебры. Однако во многих случаях, комбинируя известные методы решения уравнений и систем уравнений — метод сложения и вычитания, исключения неизвестного с помощью подстановки, введения нового неизвестного— удается найти путь к решению системы. Но в каждой отдельной задаче приходится использовать ее частные особенности для того, чтобы найти удачный метод решения. Рассмотрим несколько примеров.
Пример:
Решить систему уравнений.
Решение:
Способ 1. Из второго уравнения находим, что у = 3 — х. Подставив в первое уравнение, получаем
и, после упрощений,
Соответствующие значения для у будут такими:
Система имеет два решения.
Способ 2. Представим х³ + y³ = 18 как
Принимая во внимание второе уравнение, получим 27 — 9xy = 18, откуда ху = 1. Система
есть следствие исходной, но и исходная есть следствие преобразованной, ибо если х + у = 3; ху = 1, то
Решая преобразованную систему при помощи формул Виета, получим те же два решения:
Пример:
Решение:
Исключение одной из неизвестных величин приводит к решению уравнения четвертой степени, в котором все коэффициенты отличны от нуля. Поэтому лучше избежать этого пути. Это легко сделать, введя новую неизвестную z = xy. Тогда
Таким образом, для z получаем уравнение
откуда z₁ = 47; z₂ = 3.
Итак, данная система расщепилась на две системы:
первая из которых не имеет действительных решений, а вторая имеет следующие решения:
Указанный прием удобно применять к системам двух уравнений с двумя неизвестными, в случае если каждое из уравнений симметрично относительно х и у, т. е. если уравнения не изменяются при перемене х и у местами.
Пример:
Решить систему уравнений:
Решение:
Перемножив уравнения системы, получим
откуда xyz = ±30. Но так как ху = 5, то отсюда следует, что =5z±30 и z = ±6. Теперь х и у легко определить из второго и третьего уравнений системы. Мы приходим к двум решениям:
Пример:
Решить систему уравнений
Решение:
Возвысив обе части первого уравнения в квадрат, получим
Вычитая из этого уравнения второе уравнение данной системы, получим 2x³y³ = 686, откуда (xy)³ = 343; ху = 7. Теперь из первого уравнения данной системы находим, что 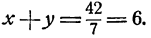
Пример:
Решить систему уравнений
Решение:
В первом уравнении раскроем скобки в каждом множителе. Затем поделим обе части обоих уравнений на ху. Получим
Теперь введем новые неизвестные 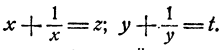
Эта система легко решается. Получаем:
Далее находим значения для х и у из уравнений
Всего получим восемь решений:
Многообразие приемов, которые могут применяться при решении систем уравнений высших степеней, неисчерпаемо, и тем не менее найти путь к решению данной системы удается далеко не всегда. Важно проявлять изобретательность при решении системы в тех случаях, когда это возможно.
Видео:СИСТЕМА УРАВНЕНИЙ второй степени 8 классСкачать

Графическое решение уравнений с одним неизвестным
Как уже было сказано, алгебраические методы решения систем уравнений далеко не всегда применимы. Но для целей практики бывает важно находить решения систем уравнений хотя бы приближенно. Эта цель хорошо достигается применением графических методов. Сначала рассмотрим применение графиков к приближенному решению одного уравнения с одним неизвестным.
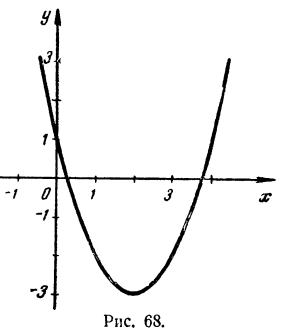
Пусть дано уравнение х²- 4x+1 = 0. Для того чтобы графически решить такое уравнение, рассматриваем неизвестное х как независимое переменное, а левую часть уравнения как функцию этой переменной, т. е. введем в рассмотрение функцию y = x²-4x+1
Решить предложенное уравнение — значит узнать, при каких значениях независимой переменной х функция у обращается в нуль.
Точки графика, соответствующие таким значениям независимой переменной, лежат на оси абсцисс, ибо ордината каждой такой точки равна нулю. Следовательно, интересующие нас точки графика являются точками пересечения графика с осью абсцисс, а корни уравнения x²-4x+1=0 являются абсциссами этих точек пересечения. При этом абсцисса каждой точки пересечения графика с осью абсцисс является корнем уравнения x²-4x+1=0
Строим график функции y = x²-4x+1 Он имеет вид параболы с вершиной в точке (2,-3) (рис. 68). По чертежу находим, что 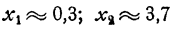
Совершенно такие же рассуждения можно применить к любому уравнению .у —0, где у есть алгебраическое выражение от неизвестной х. Именно, для графического решения такого уравнения нужно построить график выражения у, рассматриваемого как функция от переменной х, и найти точки пересечения этого графика с осью абсцисс. Абсциссы точек пересечения будут корнями уравнения. Конечно, при графическом решении уравнений корни получаются приближенно и довольно грубо, так как на чертеже произвести измерение абсцисс с высокой степенью точности невозможно.
Пример:
Решение:
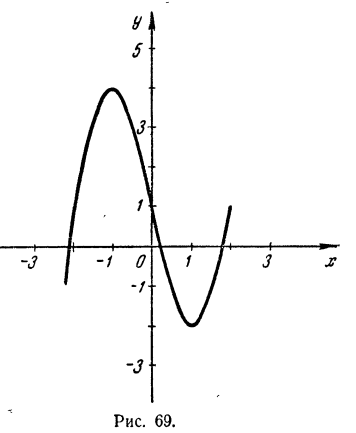
Строим график функции у = x³ — 4x + 1, вычислив предварительно таблицу значений:
По результатам этих вычислений мы видим, что при изменении х от —3 до —2 функция переходит от отрицательных значений к положительным, на участке от 0 до 1 переходит от положительных значений к отрицательным и на участке от 1 до 2 снова от отри-
нательных значений к положительным. На этих участках и следует ожидать, что график пересечет ось абсцисс.
Проводим вычисления для некоторых промежуточных значений х, взятых на этих участках с целью уточнения хода функции:
Теперь построим график по всем вычисленным точкам, соединив их плавной линией (рис. 69).
Из этого чертежа мы получаем:
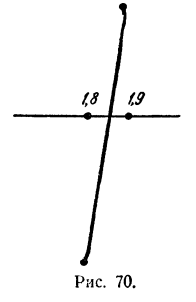
Для того чтобы уточнить значения корней, следует построить в бoльшем масштабе участки графика, примыкающие к корням, вычислив дополнительно значения функции на этих участках. Например, для уточнения корня х₃ проведем следующее вычисление:
Изобразим эти точки на чертеже, приняв большую единицу масштаба (рис. 70).
На таком малом участке изменения х мы вправе считать, что график очень близок к прямой линии. Исходя из этого предположения, получим
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Графическое решение систем двух уравнений с двумя неизвестными
Пусть дана система уравнений с двумя неизвестными х и у. Каждое из этих уравнений, взятое отдельно, определяет зависимость между величинами х и у.
Построим на одном чертеже графики этих зависимостей. Числа (x₀y₀), образующие решение системы, должны удовлетворять обоим уравнениям системы, а следовательно, точка с координатами (х₀ у₀) должна лежать на графиках обеих зависимостей, т. е. должна являться точкой пересечения этих графиков.
Обратно, координаты (x₀у₀) любой точки пересечения построенных графиков удовлетворяют обоим уравнениям системы, т. е. образуют решение системы.
Таким образом, для того чтобы графически решить систему двух уравнений с двумя неизвестными, нужно построить график для каждого из уравнений и найти точки пересечения этих графиков. Координаты каждой точки пересечения образуют решение системы.
Пример:
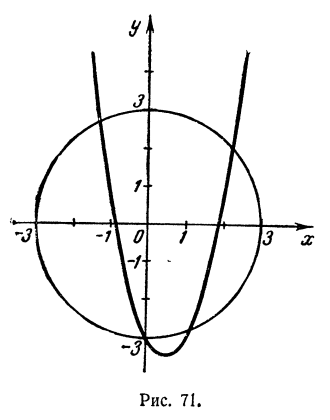
Решить графически систему уравнений
Решение:
Алгебраическое решение этой системы затруднительно. Хотя неизвестное у и легко исключается посредством подстановки в первое уравнение его выражения через дг из второго уравнения, но в результате такого исключения получается уравнение четвертой степени относительно х, решение которого выходит за рамки элементарного курса алгебры.
Обратимся к построению графиков. Графиком зависимости х² + у² = 9 является, как мы видели (гл. III, § 3, третий пример), окружность с центром в начале координат и радиусом, равным 3. Графиком зависимости у= 2х² — 2х — 3 является парабола, которую легко построить по таблице значений (рис. 71). Графики пересекаются в четырех точках, координаты которых суть приближенно (—1,2; 2,7); (0; —3); (1,1; —2,8) и (2,2: 2,0).
Следовательно, данная система имеет четыре решения
Второе решение оказывается точным. Остальные три — приближенные.
Графическое решение системы двух уравнений с двумя неизвестными почти не сложнее графического решения одного уравнения с одним неизвестным, а иногда даже проще.
Поэтому часто бывает полезно преобразовать посредством введения нового неизвестного одно уравнение с одним неизвестным в систему двух уравнений с двумя неизвестными, а затем решать эту систему графически. При таком преобразовании следует заботиться о том, чтобы построение графиков обоих уравнений полученной системы было как можно проще.
Рассмотрим несколько примеров на применение этого приема.
Пример:
Решить графически уравнение
Решение:
Представим предложенное уравнение в виде x²=x+1. Мы видим, что в левой и правой частях уравнения находятся некоторые функции от х. Решить уравнение — значит найти, при каких значениях независимого параметра обе функции принимают равные значения. Графически это означает, что нужно найти абсциссы точек пересечения графиков функций у = х² и у =х 1.
Действительно, если при х = а а² = а + 1, то это значит, что точка (а, а²) совпадает с точкой (a, a+1) и, следовательно, принадлежит как графику функции у = х², так и графику функции у = х + 1.
Очевидно и обратное. Если графики функций у = х² и у = x + 1 пересекаются в точке (а, b), то b = a² = a + 1 и, следовательно, при х = а обе функции принимают равные значения. Все сказанное можно коротко изложить так.
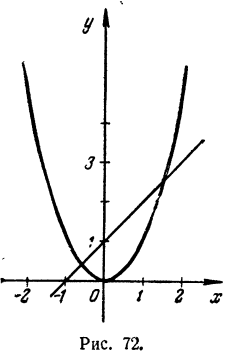
Вводим новую неизвестную y = х². Тогда данное уравнение переходит в уравнение у — х—1= 0, которое вместе с введенной зависимостью дает систему
Графиком зависимости у = х² является .парабола, графиком зависимости у = х + 1— прямая линия (рис. 72). Решение задачи дают абсциссы точек пересечения. Они равны приближенно:
Любое приведенное квадратное уравнение х² + рх + q = 0 может быть решено тем же образом, посредством преобразования в систему
Это удобно тем, что графиком первой зависимости является одна и та же парабола, а графиком второй зависимости является прямая линия, которую очень легко построить в каждом частном случае по двум точкам. Поэтому, тщательно построив в большом масштабе параболу у=х3, мы получаем возможность быстро решать любое приведенное квадратное уравнение.
Подобным образом для решения кубического уравнения, имеющего вид х³ + рх + q = 0, достаточно заготовить график функции у = х³. Абсциссы точек пересечения этого графика с прямой у + рх + q = 0 дают корни уравнения x³ + + q = 0.
Пример:
Превратив в систему, решить графически уравнение
Решение:
Это делают приемом, указанным выше. Однако это можно сделать и иначе. Именно, перепишем уравнение в виде х(х² — 4)+1=0
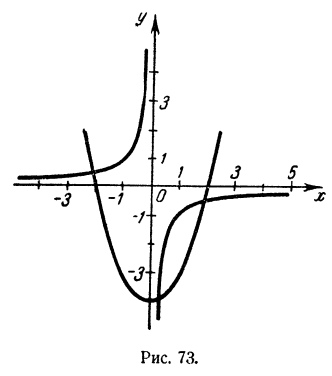
и положим х² — 4 = у. Уравнение заменится системой
Графиком первого уравнения системы является парабола, графиком второго — гипербола (рис. 73). Абсциссы точек пересечения суть
Этим приемом можно решить любое кубическое уравнение
Графиком первого уравнения является парабола, графиком второго — гипербола.
Решение уравнения четвертой степени ах⁴ + bх² + сх + d = 0 при с ≠ 0 легко сводится к определению точки пересечения двух парабол.
Для этого вводим новое неизвестное у = х² У и уравнение заменяем системой
Графиком первого уравнения является парабола с вершиной в начале координат и осью, совпадающей с осью ординат. Графиком второго уравнения тоже является парабола, но только ее ось параллельна оси абсцисс. Действительно, решив второе уравнение относительно х, мы получим
т. с. х является квадратичной функцией от у, графиком которой является парабола с осью, параллельной оси абсцисс.
Из рассмотренных примеров ясно, что каждое данное уравнение с одним неизвестным можно преобразовать а систему двух уравнений с двумя неизвестными многими способами и при выборе какого-нибудь способа следует заботиться о наиболее выгодном расположении графиков на чертеже.
Видео:Решение систем уравнений методом подстановкиСкачать

Уточнение корня уравнения или решения системы нелинейных уравнений, исходя из грубого приближения
При графическом решении корень уравнения или решение системы уравнение определяется лишь грубо приближенно. Уточнение результата за счет увеличения масштаба не очень эффективно, так как повышение точности требует пропорционального увеличения масштаба. Например, чтобы определить новую значащую цифру после занятой в десятичном разложении корня, т. е. увеличить точность в 10 раз, нужно и масштаб увеличить в 10 раз.
Однако существует весьма хорошо действующий алгебраический способ для подобного рода уточнения. Мы не будем излагать его в общем виде, а ограничимся только рассмотрением примеров его применения.
Пример:
Для уравнения x³ — 4x + 1= 0 известно приближенное значение одного из корней х ≈1,8. Требуется вычислить этот корень с большей точностью.
Решение:
Поступаем так. Положим x =1,8 + h, где h — новая неизвестная. Мы можем быть уверены, что h есть маленькое число, во всяком случае меньшее, чем 0,1. Подставив в уравнение вместо х его выражение через h, получим
Так как h² меньше h во столько же раз, во сколько h меньше единицы, для приближенного вычисления h отбросим в полученном уравнении члены с h² и h³. Получим
Для дальнейшего уточнения мы можем еще раз применить тот лее прием. Положим x≈1,86 + h₁,. Для h₁ получим, отбрасывая члены, содержащие h₁² и h₁³, приближенное уравнение
(При этом нет надобности вычислять коэффициенты при h₁² и h₁³ , ибо соответствующие члены мы все равно отбрасываем.) Отсюда h≈ 0,0008 и, следовательно,x ≈ 1,8608.
Продолжая этот прием, мы можем получить значение корня уравнения с любой степенью точности.
В общем виде идея метода такова. Если х₀ есть приближенное значение корня данного уравнения, мы полагаем в уравнении x= x₀ + h и в полученном уравнении относительно h отбрасываем члены, содержащие h выше, чем в первой степени, и решаем приближенно получившееся уравнение первой степени относительно h. Тогда число x₁ = x₀ + h оказывается, вообще говоря, значительно лучшим приближением к корню, чем исходное приближение х₀. В случае надобности процесс можно повторить.
Пример:
Для одного решения системы уравнений
известны приближенные значения х ≈ 2,2, у ≈ 2,0. Найти решение с большей точностью.
Решение:
Будем действовать тем же способом, как при уточнении корня одного уравнения с одним неизвестным. Именно, положим x = 2,2 + h; .у = 2,0 + к и, подставив в уравнение, отбросим все члены, содержащие h², k², hk, так как эти величины значительно меньше самих h и k. Получим
Решив эту систему, получим h ≈ — 0,03, k ≈ 0,07. Таким образом, уточненными значениями для х и у являются значения
Для дальнейшего уточнения можно повторить тот же процесс.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Алгебра 9 класс (Урок№25 - Решение систем уравнений второй степени.)Скачать

Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
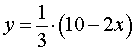 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
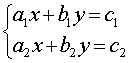 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
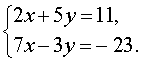 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
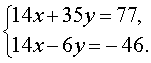 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
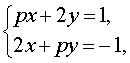 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
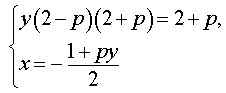 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
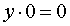
и его решением является любое число 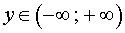
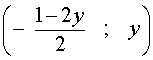
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:П.23 Некоторые приемы решения систем уравнений второй степени - Алгебра 9 класс МакарычевСкачать

Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
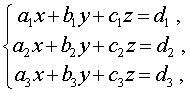 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
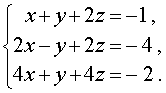 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
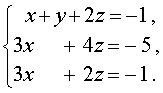 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
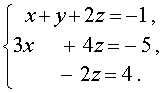 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
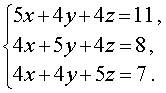 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
📺 Видео
Решение системы уравнений методом Крамера 2x2Скачать

Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Алгебра 9 класс (Урок№29 - Приёмы решения систем уравнений второй степени с двумя переменными.)Скачать

Алгебра 9 класс. Решение систем уравнений через подстановку.Скачать

Система с тремя переменнымиСкачать

Решение систем уравнений второй степени. Видеоурок 16. Алгебра 9 классСкачать

Приёмы решения систем уравнений второй степени с двумя переменными | Алгебра 9 класс #23 | ИнфоурокСкачать

Решение систем уравнений второго порядка. Практическая часть. 8 класс.Скачать

Решение систем уравнений второй степени. Видеоурок 16. Алгебра 9 класс.Скачать