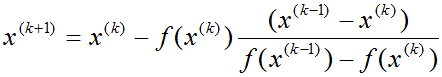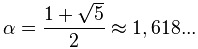Решение системы нелинейных уравнений на си

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

Определим матрицу Якоби:

(4)

Запишем(3) в виде:

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Решение для n=100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Решение для n=100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds

Решение для n=200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Программирование на C, C# и Java

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

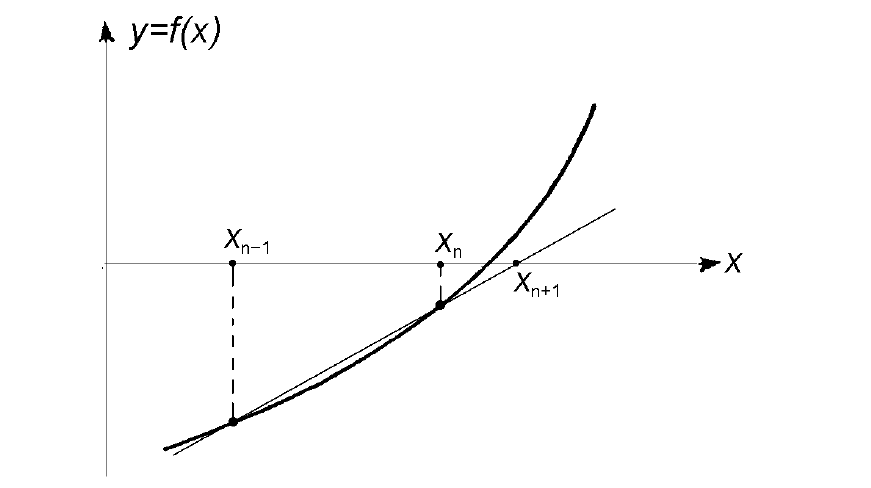
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Какие хорошие библиотеки существуют для решения системы нелинейных уравнений на C++?

в приложении C++, которое я кодирую, мне нужно решить систему non — линейные уравнения (N уравнений, N неизвестных).

системы, которые я решаю, будут довольно маленькими (до 10 уравнений/неизвестных), поэтому производительность не будет реальной проблемой. Я немного искал в интернете нелинейную библиотеку решателей, и я не мог добраться до чего-то, что выглядит простым в использовании (got to NOX и C / C++ Minpack, но оба кажутся излишним для моего потребность.)

любые мысли и идеи простых в использовании библиотек для этой цели?

Видео:Решение слау методом итераций. Метод простых итераций c++.Скачать

8 ответов

есть два варианта для вас, вы можете использовать пакеты солнечных часов, которые включают нелинейный решатель, написанный на C, я думаю. Единственная проблема, которую я нашел, заключается в том, что вам нужно дать ему хорошие начальные оценки. Второй вариант-использовать NLEQ или NLEQ2, которые, я думаю, превосходят (writtein в FORTRAN, но легко связать с C, как langages. Однако у меня были некоторые проблемы с его обнаружением. Есть хороший веб-сайт со списком возможных вариантов: http://plato.asu.edu/sub/zero.html

одна вещь должна быть ясна: нелинейное решение уравнения не легко. Это не то же самое, что решать линейные уравнения. Вы не всегда гарантированно получите решение. И ваш выбор начального условия и стратегии приращения может оказать глубокое влияние на решение, которое вы получите.

с учетом сказанного, я не могу рекомендовать конкретную библиотеку, но вы должны быть в поиске пакета линейной алгебры, который включает итерацию Ньютона-Рафсона в своем меню выбор.

численные рецепты имеет процедуру, которая будет делать работу за вас.

Это зависит от того, как нелинейные уравнения. Если они обладают некоторыми «хорошими» свойствами. наиболее очевидным является положительная полуопределенная матрица или выпуклость, могут быть специализированные алгоритмы. Я использую IBM / ILOG CPLEX для большинства моих потребностей линейного программирования. Предоставляются библиотеки, которые можно использовать в приложениях C++. Хотя я не использовал их квадратичный модуль программирования, это действительно современное состояние в высокой мощности линейной и (хорошо себя ведет) нелинейной программирование.

всегда есть GSL, но все комментарии, сделанные в других ответах, относятся и к этому:

вы смотрели МОНЕТА-ИЛИ? Это может помочь, если вы отправите свой вопрос или обмена.

Это не бесплатно, но решатель будет работать здесь.

🎬 Видео

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Уроки C++. Простые линейные уравненияСкачать

Матричный метод решения систем уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

СИСТЕМА УРАВНЕНИЙ нелинейных 9 класс алгебраСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать