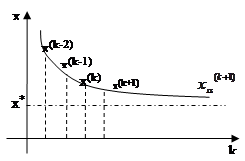
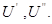Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Гаусса–Зейделя.
Проиллюстрируем сначала этот метод па примере решения системы

Предположим, что диагональные элементы а11, а22, а33отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х1, х2и х3 соответственно из первого, второго и третьего уравнений системы (2.27):



Зададим некоторые начальные (нулевые) приближения значений неизвестных: 


Используя это значение для x1 и приближение 
И наконец, используя вычисленные значения 
На этом заканчивается первая итерация решения системы (2.28) — (2.30). Теперь с помощью значений х1(1), х2(1)и х3(1)можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению: х1 = х1 (2), х2 = х2(2)и х3 = х3(2)и т.д.
Приближение с номером kможно вычислить, зная приближение с номером k– 1, как
Итерационный процесс продолжается до тех пор, пока значения х1(k), х2(k)и х3(k)не станут близкими с заданной погрешностью к значениям х1(k-1), х2(k-1)и х3(k-1).
Пример. Решить с помощью метода Гаусса – Зейделя следующую систему уравнений:
Легко проверить, что решение данной системы следующее: х1 = х2 = х3 = 1.
Решение. Выразим неизвестные х1, х2и х3соответственно из первого, второго и третьего уравнений:
В качестве начального приближения (как это обычно делается) примем х1= 0, х2 = 0, х3 = 0. Найдем новые приближения неизвестных:
Аналогично вычислим следующие приближения:
Итерационный процесс можно продолжать до получения малой разности между значениями неизвестных в двух последовательных итерациях.
Рассмотрим теперь систему п линейных уравнений с п неизвестными. Запишем ее в виде
Здесь также будем предполагать, что все диагональные элементы отличны от нуля. Тогда в соответствии с методом Гаусса – Зейделя k-e приближение к решению можно представить в виде

Итерационный процесс продолжается до тех пор, пока все значения 

Для сходимости итерационного процесса (2.31) достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных элементов):

При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т.е. для некоторых систем итерации сходятся и при нарушении условий (2.32).
Алгоритм решения системы п линейных уравнений методом Гаусса – Зейделя представлен на рис.2.6. В качестве исходных данных вводят п, коэффициенты и правые части уравнений системы, погрешность ε, максимально допустимое число итераций М, а также начальные приближения переменных xi(i=1,2,…,n).Отметим, что начальные приближения можно не вводить в компьютер, а полагать их равными некоторым значениям (например, нулю). Критерием завершения итераций выбрано условие (2.22), в котором через δобозначена максимальная абсолютная величина разности 

Для удобства чтения структурограммы объясним другие обозначения: k— порядковый номер итерации; i– номер уравнения, а также переменного, которое вычисляется в соответствующем цикле; j– номер члена вида 

- Численные методы решения систем нелинейных уравнений
- Введение
- Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
- Методы решения систем нелинейных уравнений
- Выбор модельной функции
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
- Решение систем нелинейных уравнений установившегося режима методом Зейделя
- 📹 Видео
Видео:Метод Зейделя Пример РешенияСкачать

Численные методы решения систем нелинейных уравнений
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

Обозначим через 


Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

Определим матрицу Якоби:

Запишем(3) в виде:

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

где 

При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Решение систем нелинейных уравнений установившегося режима методом Зейделя
Суть метода — найденное на текущей (k+1)-й итерации приближение напряжения узла номер (i-1) 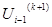
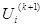
Нелинейное уравнение установившегося режима в форме баланса токов для i-го узла имеет вид:
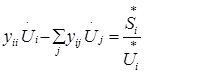
Левая часть уравнения – линейна, правая – не линейна. Т.е. уравнение нели-нейно.
Преобразуем это уравнение к виду, удобному для решения итераци-онными методами, т.е. решим его относительно Ui :
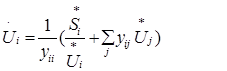
Запишем это уравнение в итерационной форме, т.е. с указанием номеров при-ближений:
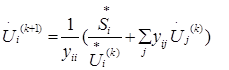
Уравнение (3) соответствует вычислительной схеме метода простой итера-ции.
Если при вычислении Ui (к+1) в правую часть выражения (3) подставлять найденные на текущей итерации приближения 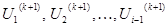
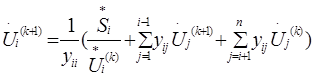
Для сети, состоящей из n узлов, нужно записать систему n таких уравне-ний, которая в итерационной форме, соответствующей методу Зейделя, имеет вид:
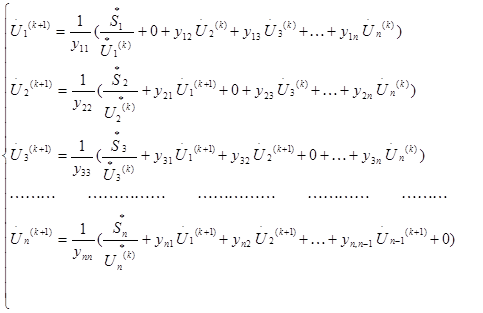
Алгоритм решения СНАУ установившегося режима методом
1. Задание условий и параметров расчета:
точность расчета E, предельное количество итераций nпр, счетчик
2. Задание начальных приближений неизвестных:
принимаем напряжение U (0) =Uном.
3. Выполнение итерации расчета для всех узлов, кроме опорного, в соот-
При расчете U1 (к+1) в правую часть 1-го уравнения подставляем к-е
приближения всех неизвестных. При расчете U2 (к+1) в правую часть
2-го уравнения подставляем только что найденное значение U1 (к+1) и
к-е приближения остальных неизвестных и т.д. При расчёте послед-
него напряжения Un (к+1) в правую часть последнего уравнения подстав
ляем найденные ранее на этой итерации (к+1)-е приближения осталь-
4. Проверка завершения итерационного процесса в соответствии с усло-
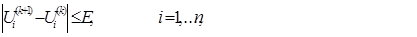
Если это условие не выполняется – возврат к п.3. и повторение расчета
при новых приближениях неизвестных.
В модели реальной электрической сети могут присутствовать специ-альные узлы, например, узлы с заданным модулем напряжения (узлы с фик-сацией модуля напряжения ФМ). В таких узлах заданными параметрами яв-ляются Uз (модуль напряжения) и Pз (активная мощность). Искомыми явля-ются 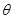
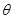
Для обеспечения фиксации модуля напряжения в ходе расчета можно выполнить следующее: переводим на каждом шаге итерационного процесса, узлы ФМ в состав нагрузочных узлов с использованием уравнений устано-вившегося режима, записанных для Q:
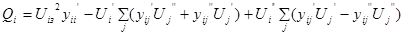
где Uiз —заданный модуль напряжения в i-ом узле,
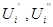
При этом должно выполняться условие:

Для того чтобы это условие выполнялось на каждом шаге итерационно-го процесса, составляющие напряжения корректируют в соответствии со следующими формулами:
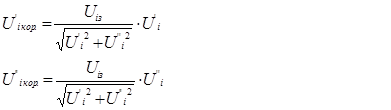
Итерационный процесс заканчивается, когда выполняется условие (6) для всех узлов:
Более точным и надежным критерием завершения итерационного про-цесса является анализ невязок уравнений.
Сходимость метода Зейделя
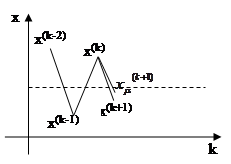
Анализируя сходимость итерационного метода – рассматриваем, прежде всего, скорость сходимости (необходимое количество итераций) и характер сходимости (колебательная или экспоненциальная).
Экспериментально выявлен ряд факторов, влияющих на скорость сходи-мости. Сходимость улучшается при:
1) более точном задании начальных приближений по напряжению;
1)2) разгрузке сильно загруженных линий;
1)3) увеличении числа генерирующих узлов с заданным модулем напря-жения (узлы ФМ) и широким диапазоном изменения реактивной мощности;
1)4) увеличение числа контуров в сети;
1)5) увеличение числа связей БП с остальными узлами;
Т.е. улучшение режима работы электрической сети – разгрузка ЛЭП, повы-шение уровней напряжений и т.д. – улучшает сходимость итерационного процесса. И наоборот – утяжеление режима, приводит к ухудшению сходи-мости и развалу итерационного процесса. Т.о. рассчитываемый режим рабо-ты электрической сети влияет на характеристики итерационного процесса.
Сходимость метода Зейделя для СНАУ установившегося режима до-вольно медленная (для сети 100-200 узлов требуется около 300-500 итера-ций).
Сходимость может быть улучшена с помощью коэффициентов ускоре-ния (метод неполной релаксации).
Пусть 
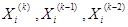
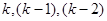
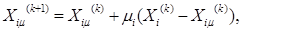
где 
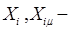


При 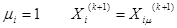
Значения коэффициента 
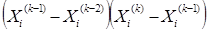
Если сходимость монотонная, то принимают 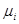

Дата добавления: 2016-05-16 ; просмотров: 366 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📹 Видео
9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Метод_Зейделя_ExcelСкачать

Метод простой итерации Пример РешенияСкачать

6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Метод ЗейделяСкачать

Численные методы. Вебинар. ( 24.12.21 ) Решение систем нелинейных уравнений.Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Зейделя в ExcelСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Метод Гуасса Зейделя, градиентный методСкачать

Решение систем линейных алгебраических уравнений методом Зейделя (устар.)Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать