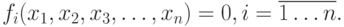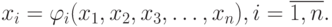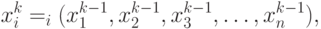Многие практические задачи сводятся к решению системы нелинейных уравнений [2, 6, 10, 12].
Пусть для вычисления неизвестных Х, х2, . х„ требуется решить систему п нелинейных уравнений:
В отличие от систем линейных уравнений не существует прямых методов решения нелинейных систем общего вида. Лишь в некоторых случаях систему (4.1) можно решить непосредственно. Например, для случая двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Для решения систем нелинейных уравнений обычно используют итерационные методы. Рассмотрим два из них — метод простой итерации и метод Ньютона.
- Метод простой итерации
- Численные методы решения систем нелинейных уравнений
- Введение
- Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
- Методы решения систем нелинейных уравнений
- Выбор модельной функции
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
- Моделирование многомерных нелинейных систем.
- Решение систем нелинейных уравнений
- Метод простых итераций
- 💡 Видео
Видео:Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Метод простой итерации
Систему уравнений (4.1) представим в следующем виде:
Запишем систему (4.2) в векторной форме: 
Для нахождения вектора корня х* = (х*,х*. х*) уравнения (4.3) часто удобно использовать метод итерации:
где начальное приближение х (0) * х*. Это грубое значение искомого корня. Заметим, что если процесс итерации (4.5) сходится, то предельное значение
обязательно является корнем уравнения (4.3). Действительно, предполагая, что соотношение (4.6) выполнено, и переходя к пределу в равенстве (4.5) прир—>оо, в силу непрерывности функции ф(х) будем иметь:
Таким образом, ?> есть корень векторного уравнения (4.3).
Рассмотрим метод простой итерации на примере системы двух нелинейных уравнений с двумя неизвестными:
Решением системы (4.7) для хе [о, Ь] и ye [с, d будут такие значения х* и у*, которые обращают эту систему в тождество. Необходимо найти х* и у* с заданной степенью точности е.
Запишем систему (4.7) в эквивалентной форме:
Последовательные приближения будут вычисляться по формулам:
где х0, уо — начальные приближения значения искомого корня.
Итерационный процесс можно считать законченным, как только выполнится неравенство
Для определения сходимости процесса имеет место следующая теорема.
Теорема. Пусть в некоторой заданной области хе[а, Ь] и ye[c,d] имеется единственное решение х*, у* системы (4.8) тогда, если:
- • ф)(х,у) и ф2(х, у) определены и непрерывно дифференцируемы в заданной области;
- • начальные приближения х0, у0и все последующие приближения х,„у„ принадлежат заданной области;
- • в рассматриваемой области выполняются неравенства:
то процесс последовательных приближений (4.9) сходится к решению системы уравнений (4.11).
Пр имер 4.1. Методом итерации приближенно решить систему 
Из графического построения (см. рис. 4.1) видно, что система имеет два решения, отличающиеся только знаком.
Ограничимся нахождением положительного решения. Из чертежа видим, что за начальное приближение положительного решения системы можно принять

Рис. 4.1. Отделение корней системы нелинейных уравнений Полагая
Аналогично,
Точное решение системы Х = 0,8261, х2 = 0,5636.
Блок-схема метода итераций приведена на рис. 4.2. Имеют место следующие обозначения неравенств (4.11):
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Численные методы решения систем нелинейных уравнений
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

Обозначим через 


Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

Определим матрицу Якоби:

Запишем(3) в виде:

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

где 

При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Моделирование многомерных нелинейных систем.
В задачах проектирования и исследования поведения реальных объектов, процессов и систем (ОПС) математические модели должны отображать реальные физические нелинейные процессы. При этом эти процессы зависят, как правило, от многих переменных.
В результате математические модели реальных ОПС описываются системами нелинейных уравнений .
Решение систем нелинейных уравнений
Дана система нелинейных уравнений
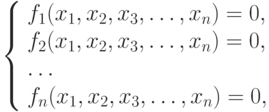 | ( 10.1) |
Необходимо решить эту систему, т.е. найти вектор 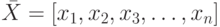

Вектор 

В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора 
Область, в которой начальное приближение 

Выбор начальной точки 
Метод простых итераций
Для применения этого метода исходная система (10.1) должна быть преобразована к виду
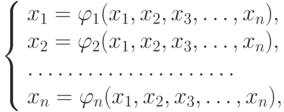 | ( 10.2) |
Далее, выбрав начальное приближение 
т.е. на каждом k-ом шаге поиска вектор переменных 
Итерационный процесс поиска прекращается как только выполнится условие
 | ( 10.3) |
При этом условие (10.3) должно выполняться одновременно по всем переменным.
Метод простых итераций используется для решения таких систем линейных уравнений, в которых выполняется условие сходимости итерационного процесса поиска, а именно:
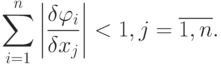 | ( 10.4) |
т.е. сумма абсолютных величин частных производных всех преобразованных уравнений системы (10.2) по j-ой переменной меньше единицы.
На рисунке 10.1 представлена схема алгоритма решения систем нелинейных уравнений методом простых итераций .
💡 Видео
Метод простой итерации Пример РешенияСкачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

10 Численные методы решения нелинейных уравненийСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Решение слау методом итераций. Метод простых итераций c++.Скачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Метод итерацийСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

5 Метод простой итерации Calc Excel Решение системы линейных уравнений СЛАУСкачать

Метод Зейделя Пример РешенияСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Решение системы линейных уравнений методом итерацийСкачать

Решение систем уравнений методом подстановкиСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать