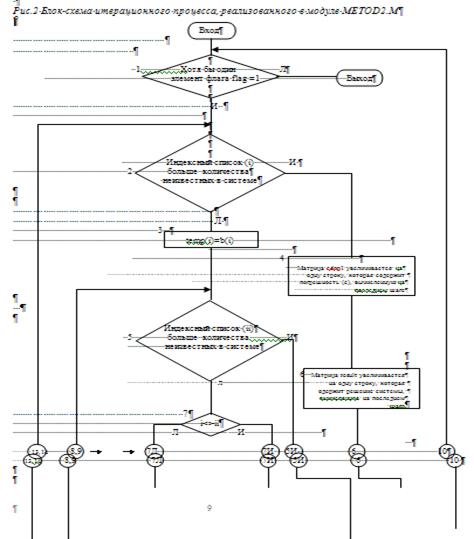
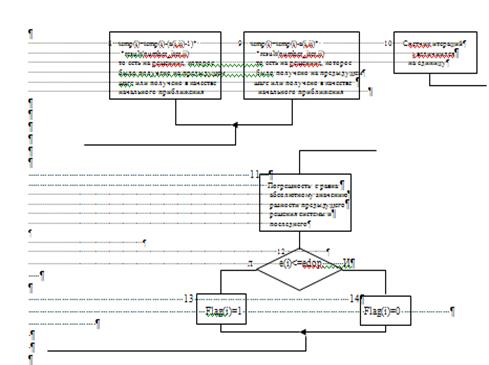
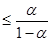Данная курсовая работа включает в себя три итерационных метода решения систем линейных алгебраических уравнений (СЛАУ):
1. Метод Якоби (метод итераций).
2. Метод Холецкого.
3. Метод верхней релаксации.
Также данная курсовая работа включает в себя: описание метода, применение метода к конкретной задаче (анализ), код программы решения вышеперечисленных методов на языке программирования BorlandC++ Builder 6.
Метод решения задачи называют итерационным , если в результате получают бесконечную последовательность приближений к решению. Основное достоинство итерационных методов состоит в том, что точность искомого решения задается. Число итераций, которое необходимо выполнить для получения заданной точности 
, является основной оценкой качества метода. По этому числу проводится сравнение различных методов.
Главным недостатком этих методов является то, что вопрос сходимости итерационного процесса требует отдельного исследования. Примером обычных итерационных методов служат: метод итераций (метод Якоби), метод Зейделя, метод верхних релаксаций.
Начнем с метода итераций или как его ещё называют метода Якоби.
Существует сиcтема A·x = f (1), где матрица A = [aij ] (i, j = 1, 2, …m ) имеет обратную матрицу; x = (x1 , x2 , x3 ,… xm ) – вектор неизвестных, f – вектор свободных членов. Систему (1) нужно преобразовать к следующему виду: 
(2) i=1, 2,…, m, где 
, 
, при этом aii
0.
Значение суммы считается равным 0, если верхний предел суммирования меньше нижнего. Тогда при i=1 уравнение имеет вид: 
(3). В методе Якоби исходят из записи системы в виде (2), итерации при этом определяют следующим образом: 
, (n=0, 1, …, n0, i=1, 2, …, m) (4).
Начальные значения 
– (i=0, 1, …, m ) задаются произвольно (в программе мы это проделываем, вводя функцию по генерации случайных чисел – «random»). Окончание итерационного процесса определяют либо заданием максимального числа итераций n0 , либо следующим условием: 
, где >0. В качестве нулевого приближения в системе (4) примем 
.
Если последовательность приближений x1 (0) , x2 (0) ,…, xm (0) , x1 (1) , x2 (1) ,…, xm (1) ,…, x1 (k) , x2 (k) ,… , xm (k) имеет предел 
, 
, то этот предел является решением системы (2).
Достаточным условием сходимости решения системы (1) является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть 
, i=1, 2, …, m.
Теперь рассмотрим второй итерационный метод – метод Зейделя , который является модификацией метода Якоби. Основная его идея заключается в том, что при вычислении (k +1) – го приближения неизвестной xi учитываются уже вычисленные ранее (k +1) – е приближения (x1 x2 ,…, xi-1 ).
Пусть дана приведенная линейная система: 
(i = 1, 2, …n ) (5). Выбираются произвольно начальные приближения корней x1 (0) , x2 (0) ,…, x n (0) , чтобы они в какой-то мере соответствовали неизвестным x1 , x2 , x3 ,…, xn .
Предполагается, что k -е приближение 
корней известно, тогда в соответствии с идеей метода строится (k +1) – е приближение по следующим формулам:
|
Если выполняется достаточное условие сходимости для системы (5) – по строкам, то в методе Зейделя выгодно расположить уравнения (6) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов: 
.
Теперь рассмотри 3 метод – метод верхних релаксаций .
Метод верхней релаксации – это есть метод Зейделя с заданным числовым параметром w.
Одним из наиболее распространенных одношаговых методов является метод верхних релаксаций, который имеет следующий вид 
(7), где w заданный числовой параметр (0 при вычислениях они могут быть записаны в один и тот же массив. При реализации метода верхних релаксаций используется следующая форма записи алгоритма вычислений 
.
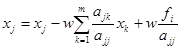
Действительно, при последовательном нахождении элемента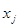 
(i+10 итерации) на каждом шаге будут использоваться найденные ранее значения, которые при k ЧИТАТЬ ПОЛНОСТЬЮ «
- Курсовая работа: Метод простой итерации для решения систем линейных алгебраических уравнений
- Новосибирский государственный технический университет
- Курс: «Численные методы»
- Пояснительная записка к курсовой работе на тему
- «Метод простой итерации для решения систем линейных алгебраических уравнений»
- База знаний студента. Реферат, курсовая, контрольная, диплом на заказ
- Итерационные методы решения систем линейных уравнений с неединственными коэффициентами — Математика
- 📺 Видео
Видео:Решение системы линейных уравнений методом итерацийСкачать
Курсовая работа: Метод простой итерации для решения систем линейных алгебраических уравнений
| Название: Метод простой итерации для решения систем линейных алгебраических уравнений Раздел: Рефераты по математике Тип: курсовая работа Добавлен 07:19:45 30 марта 2011 Похожие работы Просмотров: 4206 Комментариев: 22 Оценило: 5 человек Средний балл: 5 Оценка: неизвестно Скачать |
x 0 1 |
Производя итерации, получим последовательность векторов x ( 1 ) , x ( 2) ,…, x ( k ) ,… Доказано, что если элементы матрицы C удовлетворяют одному из условий
(i=1,2,…,n) (2.2.4)
(j=1,2,…,n) (2.2.5),
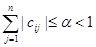
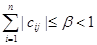
то процесс итерации сходится к точному решению системы x при любом начальном векторе x (0) , то есть
x=
x ( k ) .
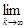
Таким образом, точное решение системы получается лишь в результате бесконечного процесса, и всякий вектор x ( k ) из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения x ( k ) дается одной из следующих формул:
| xi — xi ( k ) |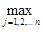 
| xi ( k ) — xi ( k -1 ) |, (2.2.4′)
если выполнено условие (2.2.4), или
| xi — xi ( k ) |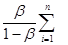 
| xi ( k ) — xi ( k -1 ) |, (2.2.5′)
если выполнено условие (2.2.5). Эти оценки можно еще усилить соответственно так:
max | xi — xi ( k ) |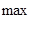 
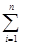
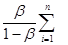
| xi ( k ) — xi ( k -1 ) |, (2.2.4»)
| xi — xi ( k ) | | xi ( k ) — xi ( k -1 ) |. (2.2.5»)
Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности.
Начальный вектор x ( 0 ) может быть выбран, вообще говоря, произвольно. Иногда берут x ( 0 ) =f. Однако, наиболее целесообразно в качестве компонент вектора x ( 0 ) взять приближенные значения неизвестных, полученные грубой прикидкой.
Приведение системы (2.2.1) к виду (2.2.2) можно осуществить различными способами. Важно только, чтобы выполнялось одно из условий (2.2.4) или (2.2.5). Ограничимся рассмотрением двух таких способов.
Первый способ. Если диагональные элементы матрицы А отличны от нуля, то есть
aii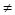
0 ( i=1,2,…,n),
то систему (2.2.1) можно записать в виде
x1 = 
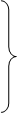
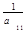
(b1 — a12 x2 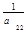— … — a1n xn ),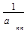
x2 = 
(b2 — a21 x1 — a23 x3 -… — a2n xn ),(2.2.6)
xn = 
(bn — an1 x1 — … — an n-1 xn-1 ).
В этом случае элементы матрицы С определяются следующим образом:
(ij), cii =0,
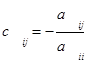
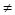
и тогда условия (2.2.4) и (2.2.5) соответственно приобретают вид
(i=1,2,… ,n), (2.2.7)
(j=1,2,… ,n). (2.2.8)
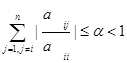
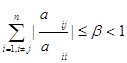
Неравенства (2.2.7), (2.2.8) будут выполнены, если диагональные элементы матрицы А удовлетворяют условию
(i=1,2,… ,n), (2.2.9)
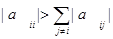
то есть если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Второй способ позволяет записать систему (2.2.1) в виде
x1 = b1 — (a11 -1)x1 — a12 x2 — … — a1n xn ,
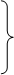
и пояснений не требует.
3. Описание программного обеспечения
3.1 Общие сведения
Данное программное обеспечение представлено в виде двух основных программных модулей (файлы metod1.m и metod2.m) и четырех вспомогательных модулей (файлы system_a.m, system_b.m, x0.m и x_ok.m).
3.2 Функциональное назначение программы
Данное программное обеспечение предназначено для решения систем линейных алгебраических уравнений вида Ax=b методом простой итерации.
Программный модуль metod1.m содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, использующий первый способ перехода от системы вида F(x)=xк системе вида x=
(x) (см. п.2.2.).
Программный модуль metod2.m также содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, но использующий второй способ перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.).
Вспомогательный модуль system_a.m содержит матрицу А исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль system_b.m содержит столбец b исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль x0.m содержит столбец начального приближения к точному решению исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль x_ok.m содержит столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b.
Замечание: модули system_a.m, system_b.m, x0.m всегда описывает сам пользователь, работающий с данным программным обеспечением, в зависимости от решаемой системы линейных алгебраических уравнений.
Модуль x_ok.m также может быть описан пользователем, но он не является обязательным, так как точного решения обычно у пользователя нет. Отсутствие данного модуля не влияет на правильность работы программы, он является вспомогательным и необходим лишь для оценки погрешности полученного решения (как этого требует задание), но что обычно не нужно в прикладном использовании данного программного обеспечения.
3.3 Вызов и загрузка программы
Для вызова программы на выполнение необходимо загрузить программу MatLab 3.5f (и выше), затем в командной строке данной среды набрать имя одного из программных модулей (metod1.m или metod2.m).
3.4 Входные данные
1. system_а — матрица А исходной системы линейных алгебраических уравнений вида Ax=b, считывающаяся из модуля system_а.m;
2. system_b — столбец b исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля system_b.m;
3. x0 — столбец начальных приближений, считывающийся из модуля x0.m;
4. x_ok — столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля x_ok.m.
Замечание: если отсутствует модуль x_ok.m, то переменная x_ok не передается в основные программные модули.
3.5 Выходные данные
Выходными данными программных модулей metod1.m и metod2.m является файл total — файл-отчет, содержащий результаты одного или нескольких итерационных процессов, а именно: полученные решения, погрешности полученного решения, скорость сходимости метода, время счета, число операций.
3.6 Описание алгоритмов
Исходный текст модуля metod1.m представлен в Приложении1.
Сначала производится инициализация переменных result (решение системы линейных алгебраических уравнений), temp (промежуточные значения решения системы линейных алгебраических уравнений на каждом шаге итерации), size_system (размерность системы), flag (флаг для остановки итерационного процесса), edop1 (абсолютное значение k-го и (k+1)-го решения), number_iter (количество итераций), time (время счета), number_oper (количество операций), a (матрица А системы Ax=b), b (столбец b системы Ax=b). После этого на дисплей выводится запрос допустимой погрешности. Когда погрешность введена, происходит очистка экрана, обнуление встроенного в MatLab счетчика операций с плавающей точкой, запоминание текущего момента времени.
Далее после этих приготовлений запускается цикл перехода от системы вида F(x)=xк системе вида x=(x) первым способом (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.1.
Как только заканчивается цикл итераций, происходит повторное запоминание текущего момента времени и количества операций с плавающей точкой. По окончании данных действий происходит подсчет времени счета, как разности ранее запомненных моментов времени. Далее происходит запись полученного решения в файл total.
Далее производится проверка, существует ли файл x_ok.m. Если таковой имеется, то высчитывается погрешность полученного решения и записывается в файл total.
После вышеописанных действий происходит последняя запись в файл total сведений о количестве шагов, необходимых для сходимости метода, времени счета, числе операций.
Затем происходит подготовка масштаба будущего графика итерационного процесса и непосредственно его построение, после которого выполнение программы прерывается до нажатия любой клавиши.
И наконец, когда какая-либо клавиша будет нажата, произойдет очистка экрана и построение графиков зависимости погрешности от шага итерации.
Исходный текст модуля metod2.m представлен в Приложении1.
Алгоритм данного программного модуля аналогичен алгоритму модуля metod1.m. Единственное отличие — реализация цикла перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.2.
3.7 Используемые программные и технические средства
Все модули данного программного обеспечения написаны на языке MatLab в редакторе NortonEditor из комплекса утилит NortonUtilities 8.0.
Для правильной работы программ metod1 и metod2 необходима операционная система MSDOS (любой версии) или операционная система Windows95, программа MatLab 3.5f (или выше), а также персональный компьютер, совместимый с IBMPC 386SX (или выше).
4. Описание тестовых задач
В качестве тестовых задач рассмотрим две системы линейных алгебраических уравнений:
1,02x1 — 0,25x2 — 0,30 x3 =0,515
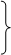
В качестве начального приближения x ( 0 ) возьмем два вектора: x ( 0) =(1000,1000,1000); x ( 0 ) =(1,1,1).
0,22x1 + 0,02x2 + 0,12x3 + 0,13x4 = -3
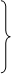
Точного решения нет.
В качестве начального приближения x ( 0 ) возьмем два вектора: x ( 0) =(0,10,20,30); x ( 0 ) =(-270,-503,1260,-653 ).
Все вычисления будем проводить при заданной точности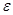 
=0.001 .
5. Анализ результатов счета , выводы
Результаты вычислений тестовых систем линейных алгебраических уравнений представлены в виде файлов-отчетов, которые приведены в Приложении2, а также в виде графиков итерационных процессов и графиков зависимостей погрешностей решений исходных систем линейных алгебраических уравнений от шага итерации, которые приведены в Приложении3.
Анализируя эти результаты, можно сделать следующие выводы.
Во-первых, количество итераций сильно зависит от матрицы А исходной системы уравнений вида Ax=b. Чем ближе диагональные элементы матрицы А к нулю, тем больше итераций требуется для того, чтобы решить исходную систему линейных алгебраических уравнений.
Во-вторых, на количество шагов влияет начальное приближение. Чем оно ближе к точному решению, тем меньше требуется шагов для сходимости метода. Следует отметить, что в рассматриваемых примерах достаточно точное начальное приближение требует количества итераций приблизительно в 1,7-2,0 раза меньше, чем произвольное, достаточно далеко отстоящее от точного решения, приближение.
В-третьих, скорость сходимости метода зависит от того, каким способом реализован переход от системы вида F(x)=xк системе вида x=(x).
Анализ счета показывает, что если диагональные элементы матрицы А не близки к нулю, то при любом приближении (достаточно точном и не очень) количество шагов, требующихся для сходимости метода, практически не зависит от способа перехода от системы вида F(x)=xк системе вида x=(x). А если элементы диагонали матрицы A близки к нулю и приближение недостаточно точное, то метод сходится быстрее, если в нем реализован первый способ перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.).
Число операций для решения исходной системы линейных алгебраических уравнений при использовании первого способа перехода требуется несколько меньше, чем для решения исходной системы линейных алгебраических уравнений при использовании второго способа перехода. Это удалось выяснить при решении системы
(4.1) при приближении x ( 0 ) =(1,1,1), так как в этом случае для обоих способов потребовалось одинаковое количество шагов для сходимости и одинаковое время счета, но различное число операций с плавающей точкой.
Время счета, как видно из результатов решения систем (4.1) и (4.2) линейно зависит от количества шагов и числа операций. Чем показатели последних выше, тем больше время счета.
Наконец, погрешности полученных решений, как видно из файла-отчета, не превышает заданную погрешность .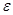
Исходя из тестовых систем линейных алгебраических уравнений и результатов их решения, можно сделать следующие выводы.
Метод простой итерации (при любом способе перехода от системы вида F(x)=xк системе вида x=(x) ) сходится быстро, если диагональные элементы матрицы А системы Ax=b близки к единице, а остальные — близки к нулю, и приближение достаточно близко к точному решению. Но при решении систем Ax=b с матрицей А, отличной от вышеописанной, метод сходится при первом способе перехода более быстро в случае, если начальное приближение далеко отстоит от точного решения, а если приближение достаточно близко лежит к точному решению, то при втором способе перехода метод сходится несколько быстрее, чем при первом.
Итак, можно сказать, что применение в прикладных задачах данного метода оправданно, но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений.
В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=xк системе вида x=(x).
Вообще говоря, метод простой итерации не отличается повышенной сходимостью (может вообще не сойтись), но если он сходится, то этот метод обычно имеет высокую точность счета и достаточно высокую скорость сходимости. Следует отметить, что все вышеперечисленное зависит от самой исходной системы Ax=b и способа перехода к системе вида x=(x). Если метод не сходится, значит не соблюдаются условия сходимости метода или используется неудачный переход к системе x=(x).
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать
База знаний студента. Реферат, курсовая, контрольная, диплом на заказ
Видео:Решение систем линейных уравнений методом простой итерации в ExcelСкачать
Итерационные методы решения систем линейных уравнений с неединственными коэффициентами — Математика
Министерство образования Российской Федерации
Пермский Государственный Технический Университет
Итерационные методы решения линейных систем с неединственными коэффициентами
Елисеев Александр Сергеевич, ММ-05-2
Грайфер Лазарь Борисович
§1. Уточнение решения 4
§2. Метод простых итераций 7
§3. Метод Гаусса – Зейделя 14
§4. Применение итерационных методов 16
Список использованной литературы 19
Все используемые на практике методы решения систем линейных алгебраических уравнений можно разделить на две большие группы: точные методы и итерационные методы.
Под точным методом решения понимается метод, позволяющий теоретически получить точное значение всех неизвестных в результате конечного числа арифметических операций. (метод Крамера)
Итерационные методы позволяют получить решение лишь в виде предела последовательности векторов, построение которого производится единообразным процессом, называется процессом итерации, или последовательных приближений.
Вдобавок, итерационные методы находят широкое применение и при решении еще одной вычислительной задачи линейной алгебры, называемой полной проблемой собственных значений (отыскание всех собственных значений и отвечающих им собственных векторов заданной матрицы), т.к. намного удобнее вычислить предел некоторых числовых последовательностей без предварительного определения коэффициентов характеристического многочлена.
Преимуществом итерационных методов является удобное применение в современной вычислительной технике, т.к. решения, полученные с помощью прямых методов обычно содержат погрешность. Итерационные методы же позволяют получить решение данной системы с заранее определенной погрешностью. Явным преимуществом является значительное превосходство над точные методы по скорости и удобнее реализуются на практике.
§1. Уточнение решения
Полученные с помощью прямых численных методов решения обычно содержат погрешность, вызванную округлениями при выполнении операций над числами с плавающей точкой. В некоторых случаях эти погрешности могут оказаться недопустимо большими. Рассмотрим один из методов уменьшения погрешности численного решения СЛАУ.
Найдем решение системы линейных уравнений
Пусть с помощью некоторого метода получено приближенное решение (начальное приближение к решению). Подставив в (1.1), получим
Обозначим за погрешность полученного решения, — невязка.
Вычитаем (1.2) из (1.1), с учетом введенных обозначений
Решив эту систему получим новое значение погрешности , которое используем в качестве поправки к приближенному решению , получая таким способом новое приближение (следующее приближение к решению):
Таким же способом найдем следующее приближение и следующую поправку к приближению . Подобным образом будем искать очередные значения погрешности и поправки, пока погрешность не станет достаточно малым. Таким образом мы найдем приближенное решение системы с заданной точностью.
Рассмотренный выше процесс фактически является итерационным методом решения системы линейных уравнений, при этом следует отметить небольшой объем вычислений, т.к. на каждой итерации решаются системы уравнений вида (1.3) с одной и той же матрицей, т.е. нет необходимости преобразовывать матрицу. Такой подход позволяет строить экономичные с точки зрения машинного времени алгоритмов.
Следует заметить, что если при увеличении числа итераций приближенное решение стремится к точному:
то итерационный метод называют сходящимся.
Наличие сходимости и достижения заданной точности на практике можно определить (приближенно) несколькими способами. Так, при заданной погрешности
Здесь в (1.4) отличие векторов и на «ε» понимается как малость модуля их разности. В (1.5) – малость разностей всех компонентов вектора, в (1.6) в смысле малости относительных разностей компонент. В случае, когда система не является плохо обусловленной, то в качестве критерия достижения нужной точности можно принять условие малости невязки:
§2. Метод простых итераций (метод Якоби)
Рассмотрим квадратную систему линейных уравнений с вещественными коэффициентами, которую запишем в матричном виде (1.1).
Предполагая однозначную разрешимость системы (1.1), заменим матричное уравнение эквивалентным ему уравнением:
где τ – вещественное число, называемое стационарным параметром. С помощью (2.1) составим итерационную последовательность векторов
при произвольном выборе нулевого приближения.
Таким образом, метод простой итерации сводится к замене точного решения системы (1.1) k – ой итерацией с достаточно большим номером k.
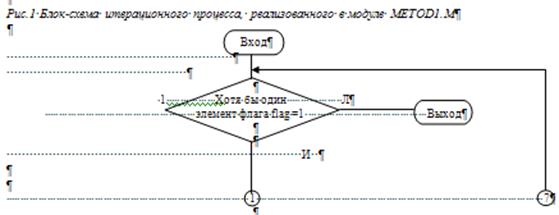
Графически метод Якоби можно представить следующим образом:
Рис. 1. Схема выполнения метода Якоби
где Е – единичная матрица.
Введем в рассмотрение норму вектора в пространстве и операторную норму квадратной матрицы порядка число число на множестве всех ненулевых векторов на множестве всех векторов
Из (2.4) вытекает неравенство, справедливое для любой матрицы и любого вектора
Из матричного уравнения погрешности (2.3) и неравенства (2.5) получаем, что для любого номера
Теорема 2.1. Для того, чтобы итерационная последовательность (2.2) при любом выборе начального приближения и при данном значении параметра сходилась к точному решению системы (1.2), достаточно, чтобы было выполнено условие
При этом итерационная последовательность сходится со скоростью геометрической последовательности со знаменателем
В случае если матрица является симметричной, условие является необходимым условием сходимости итерационной последовательности при любом выборе нулевого приближения.
Для практических же целей недостаточно установить факт сходимости последовательности итераций. Центральным вопросом является оценка скорости сходимости. Очень важно знать, как наилучшим способом распорядиться стационарным параметром для того, чтобы получить наиболее быструю сходимость.
Пусть задана точность — точность, с которой необходимо получить решение системы. Требуется найти итерацию с таким номером
Из (2.6) и Теоремы 2.1 следует, что — точности, следует выбрать параметр так, чтобы получить минимум функции
Считая матрицу симметричной и положительно определенной, мы приходим к следующей задачей оптимизации: найти минимум функции
Теорема 2.2 (Теорема А.А. Самарского). Пусть матрица является симметричной и положительно определенной, а матрица положительно определенной. Тогда для того, чтобы итерационная последовательность
при любом выборе нулевого приближения сходилась к точному решению системы
При дополнительно предположении о том, что матица является симметричной, условие (2.10) не только достаточно, но и необходимо для сходимости указанной итерационной последовательности с любым нулевым приближением
Выражение (2.9), где представляет себя некоторую «легко обратимую» квадратную матрицу — стационарный параметр, получается из выражения (2.2) . Такой метод является более общим методом по сравнению с методом простой итерации и называется «неявным методом простой итерации».
Перейдем теперь к оценке сходимости общего неявного метода простой итерации. Для этого выясним вопрос о выборе стационарного параметра
Предположим, что является симметричной и положительно определенной. С помощью таких матриц естественно ввести так называемое «энергетическое скалярное произведение» двух произвольных векторов и Такое скалярное произведение будем обозначать это скалярное произведение можно записать в виде С помощью последнего равенства легко проверяется справедливость для введенного нами скалярного произведения четырех аксиом скалярного произведения.
Далее естественно ввести «энергетическую норму» вектора
Две различных нормы одной и той же системы векторов и называются эквивалентными, если существуют такие положительные постоянные и
Энергетическая и обычная нормы вектора являются эквивалентными, а это позволяет утверждать, что последовательность
Теорема 2.3 Пусть матрица и симметричны и положительно определены, — погрешность общего неявного метода простой итерации. Тогда для того, чтобы при было справедливо неравенство
Применим Теорему 2.3 для нахождения значения стационарного параметра
Так как обе матрицы и являются симметричными и положительно определенными, то существуют такие постоянные и и в этих неравенствах нам заданы. Сопоставляя это неравенство с условием (2.12), мы получим, что минимальное значение достигается при условии и минимальное значение
Частным случаем приведенного рассмотрения является явный метод простой итерации, для которого справедливы все полученные выше результаты.
§3. Метод Гаусса-Зейделя
Рассмотрим еще один итерационный метод решения систем линейных алгебраических уравнений. Метод Гаусса-Зейделя заключается в последовательном выражении неизвестных. Этот метод является одним из самых распространенных и наиболее легко программируемых.
Пусть задана СЛАУ
Предположим, что диагональные элементы не нулевые (в противном случае можно переставить уравнения). Выразим неизвестные из каждого уравнения:
Зададим некоторые начальные (нулевые) приближения значений неизвестных: и т.д. до
На этом заканчивается первая итерация решения системы. Используя теперь полученные приближения таким же образом проводи вторую итерацию.
Итерационный процесс продолжается до тех пор, пока значения неизвестных не станут отличаться от предыдущих приближений на
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных коэффициентов):
При этом хотя бы для одного уравнения это неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но не являются необходимыми, т.е. для некоторых систем метод сходится и при нарушении условий.
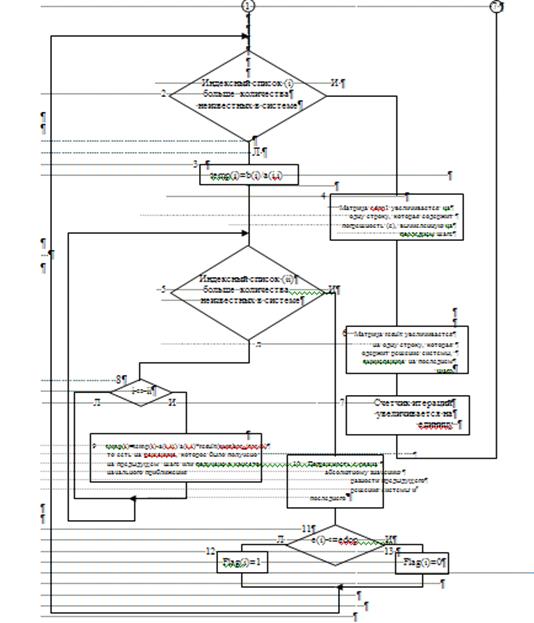
Графически метод Зейделя можно представить следующим образом:
Рис. 2. Схема выполнения метода Гаусса-Зейделя
§4. Применение итерационных методов
Покажем применение итерационных методов на конкретном примере. Для этого, решим систему уравнений вида
Возьмем для удобства матрицу двухдиагональной, и размерностью , и произвольный вектор , т.е. матрицы вида
Так как можно доказать, что все собственные числа матрицы по модулю меньше единицы:
То для решения системы (1.1) с заданными коэффициентами (4.1) можно применить как итерационный метод Якоби, так и метод Гаусса-Зейделя.
Точным решением системы является вектор .
После применения итерационные методы Якоби и Гаусса-Зейделя были получены следующие результаты:
📺 Видео
Метод Ньютона (метод касательных) Пример РешенияСкачать
Решение системы уравнений методом ГауссаСкачать
Метод простой итерации Пример РешенияСкачать
Решение системы линейных уравнений методом простых итераций в MS ExcelСкачать
8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать
Метод_Зейделя_ExcelСкачать
Решение слау методом итераций. Метод простых итераций c++.Скачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Лекция 5, Итерационные методы решения систем линейных уравненийСкачать
1 3 Решение нелинейных уравнений методом простых итерацийСкачать
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать
Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать
2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать
Вычмат. ЛЭТИ. практика. 2 курс. Итерационные методы решения СЛАУ (1)Скачать
Решение системы уравнений методом Гаусса 4x4Скачать
Метод итерацийСкачать
