Решение системы линейных уравнений методом гаусса питон

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Решение систем линейных уравнений с помощью Python’s Numpy

Два или более линейных уравнения с одинаковым набором переменных называются системой линейных уравнений. Мы можем решить эти переменные в Python с помощью Numpy.

• Автор записи

Автор: Guest Contributor
Дата записи

Библиотека Numpy может использоваться для выполнения различных математических/научных операций, таких как матричные кросс-и точечные произведения, поиск значений синуса и косинуса, преобразование Фурье и манипулирование формой и т. Д. Слово Numpy-это сокращенное обозначение “Числового питона”.

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Numpy Python.

Что такое Система линейных уравнений?

В математике система линейных уравнений (или линейная система) представляет собой совокупность двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Чтобы решить приведенную выше систему линейных уравнений, нам нужно найти значения переменных x и y . Существует множество способов решения такой системы, таких как Исключение переменных, Правило Крамера, Метод сокращения строк и Матричное решение. В этой статье мы рассмотрим матричное решение.

В матричном решении система решаемых линейных уравнений представляется в виде матрицы AX . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:

Чтобы найти значение переменных x и y в Уравнение 1 , нам нужно найти значения в матрице X . Для этого мы можем взять точечное произведение обратной матрицы A и матрицы B , как показано ниже:

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричный точечный продукт, ознакомьтесь с этой статьей .

Решение системы линейных уравнений с Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений необходимо выполнить две операции: инверсию матрицы и матричное точечное произведение. Библиотека Numpy из Python поддерживает обе эти операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

Теперь давайте посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv() и dot()

Во-первых, мы найдем обратную матрицу A , которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A в Python. Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list , который далее содержит два списка: [4,3] и [-5,9] . Эти списки являются двумя строками в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу array , как показано ниже:

Чтобы найти обратную матрицу, матрица передается в метод linalg.inv() модуля Numpy:

Следующий шаг-найти точечное произведение между обратной матрицей A и матрицей B . Важно отметить, что матричное точечное произведение возможно только между матрицами , если внутренние размеры матриц равны , то есть количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Для поиска точечного продукта с помощью библиотеки Numpy используется функция linalg.dot () . Следующий скрипт находит точечное произведение между обратной матрицей A и матрицей B , которая является решением уравнения 1 .

Вот, 2 и 4 являются ли соответствующие значения для неизвестных x и y in Уравнение 1 . Для проверки, если вы подключаете 2 на месте неизвестного x и 4 на месте неизвестного y в уравнении 4x + 3y вы увидите , что результат будет равен 20.

Давайте теперь решим систему из трех линейных уравнений, как показано ниже:

Приведенное выше уравнение можно решить с помощью библиотеки Numpy следующим образом:

В приведенном выше скрипте методы linalg.inv() и linalg.dot() соединены вместе. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

Значение для неизвестных x , y и z равно 5, 3 и -2 соответственно. Вы можете подключить эти значения в Уравнение 2 и проверить их правильность.

Использование метода solve()

В предыдущих двух примерах мы использовали методы linalg.inv() и linalg.dot() для нахождения решения системы уравнений. Однако библиотека Numpy содержит метод linalg.dsolve () , который может быть использован для непосредственного нахождения решения системы линейных уравнений:

Вы можете видеть, что выход такой же, как и раньше.

Реальный Пример

Давайте посмотрим, как система линейных уравнений может быть использована для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, то какова была цена одного манго и одного апельсина?

Эта задача легко решается с помощью системы двух линейных уравнений.

Допустим, цена одного манго равна x , а цена одного апельсина равна y . Вышеприведенная проблема может быть преобразована следующим образом:

Решение приведенной выше системы уравнений показано здесь:

Результат показывает, что цена одного манго составляет 10 долларов, а цена одного апельсина-15 долларов.

Видео:Решение системы уравнений методом ГауссаСкачать

Прямые методы линейной алгебры

Одной из основных задач вычислительной математики является проблема решения систем линейных алгебраических уравнений с вещественными ко- эффициентами. Для нахождения приближенного решения систем уравнений используются прямые и итерационные методы. Математический аппарат ли- нейной алгебры базируется на понятиях нормы вектора и матрицы, числа обусловленности. Рассматриваются классические методы исключения неиз- вестных, отмечаются особенности решения задач с симметричной веществен- ной матрицей.

Видео:СЛАУ в PythonСкачать

Метод исключения Гаусса

Начнем с обсуждения того, как можно легко решать треугольные системы. Затем опишем приведение системы общего вида к треугольной форме при помощи преобразований Гаусса. И, наконец, учитывая то, что полученный метод ведет себя очень плохо на нетривиальном классе задач, рассмотрим концепцию выбора ведущих элементов.

Треугольные системы

Рассмотрим следующую треугольную ( 2times 2 )-систему: $$ begin l_ & 0 \ l_ & l_ end begin x_1\ x_2 end = begin b_1\ b_2 end $$

Если ( l_, l_ ne 0 ), то неизвестные могут быть определены последовательно: $$ begin x_1 &= b_1/l_,\ x_2 &= (b_2 — l_x_1)/l_ end $$

Это ( 2times 2 )-версия алгоритма, известного как прямая подстановка. Общую процедуру получаем, разрешая ( i )-е уравнение системы ( Lx = b ) относительно ( x_i ): $$ x_i = left( b_i — sum_^ l_ x_j right)/l_. $$

Если вычисления выполнить для ( i ) от ( 1 ) до ( n ), то будут получены все компоненты вектора ( x ). Заметим, что на ( i )-м шаге необходимо скалярное произведение векторов ( L(i,1:i-1) ) и ( x(1:i-1) ). Так как ( b_i ) содержится только в формуле для ( x_i ), мы можем записать ( x_i ) на месте ( b_i ).

Прямая подстановка

Предположим, что ( L in mathbb^ ) — нижняя треугольная матрица и ( b in mathbb^n ). Следующий код Python заменяет ( b ) на решение системы ( Lx = b ). Матрица ( L ) должна быть невырождена.

Аналогичный алгоритм для верхней треугольной системы ( Ux = b ) называется обратная подстановка. Вот формула для ( x_i ): $$ x_i = left( b_i — sum_^ u_ x_j right)/u_. $$ и снова ( x_i ) можно записать на месте ( b_i ).

Обратная подстановка

Если матрица ( U in mathbb^ ) верхняя треугольная и ( b in mathbb^n ), то следующий код Python заменяет ( b ) на решение системы ( Ux = b ). Матрица ( U ) должна быть невырождена.

Отметим, что при реализации формул прямой и обратной подстановки мы использовали срезы массивов (см. раздел ref). В первом алгоритме L[i,:i] означает, что берется из строки двумерного массива с индексом i все элементы с нулевого до i-1 -го включительно, а b[:i] — элементы массива b с индексами от 0 до i-1 включительно. Во втором алгоритме используются срезы U[i,i+1:] , содержащий от i+1 -го до последнего (включительно) элементы i -той строки, и b[i+1:] с элементами от i+1 -го до последнего (включительно). Кроме того использовалась функция dot модуля numpy , которая вычисляет скалярное произведение двух векторов. Таким образом, мы здесь использовали векторизованные вычисления.

( LU )-разложение

Как мы только что видели, треугольные системы решаются «легко». Идея метода Гаусса — это преобразование системы (1) в эквивалентную треугольную систему. Преобразование достигается соответствующих линейных комбинаций уравнений. Например, в системе $$ begin 3x_1 + 5x_2 &= 9,\ 6x_1 + 7x_2 &= 4, end $$ умножая ее первую строку на 2 и вычитая ее из второй части, мы получим $$ begin 3x_1 + 5x_2 &= 9,\ -3x_2 &= -14. end $$

Это и есть метод исключений Гаусса при ( n=2 ). Дадим полное описание этой важной процедуры, причем опишем ее выполнение на языке матричных разложений. Данный пример показывает, что алгоритм вычисляет нижнюю треугольную матрицу ( L ) и верхнюю треугольную матрицу ( U ) так, что ( A = LU ), т.е. $$ begin 3 & 5 \ 6 & 7 end = begin 1 & 0 \ 2 & 1 end begin 3 & 5 \ 0 & -3 end $$ Решение исходной задачи ( Ax = b ) находится посредством последовательного решения двух треугольных систем: $$ Ly = b, quad Ux = y quad Rightarrow Ax = LUx = Ly = b $$

Матрица преобразования Гаусса.

Чтобы получить разложение, описывающее исключение Гаусса, нам нужно иметь некоторое матричное описание процесса обнуления матрицы. Пусть ( n=2 ), тогда как ( x_1 ne 0 ) и ( tau = x_2/x_1 ), то $$ begin 1 & 0 \ -tau & 1 end begin x_1\ x_2 end = begin x_1\ 0 end $$ В общем случае предположим, что ( x in mathbb^n ) и ( x_k ne 0 ). Если $$ tau^ = [ underbrace_k, tau_, ldots, tau_n ], quad tau_i = frac quad i = k+1, k+2, ldots, n $$ и мы обозначим $$ begin tag M_k = I — tau^ e_k^T, end $$ где $$ begin e_k^T &= [underbrace_, 1, underbrace_],\ I &= [e_1, e_2 ldots, e_n] end $$ то $$ M_k x = begin 1 & dots & 0 & 0 & dots & 0 \ vdots & ddots & vdots & vdots & ddots & vdots \ 0 & dots & 1 & 0 & dots & 0 \ 0 & dots & -tau_ & 1 & dots & 0 \ vdots & ddots & vdots & vdots & ddots & vdots \ 0 & dots & -tau_n & 0 & dots & 1 end begin x_1\ vdots \ x_k \ x_ \ vdots \ x_n end = begin x_1\ vdots \ x_k \ 0\ vdots \ 0 end $$

Матрица ( M_k ) — это матрица преобразования Гаусса. Она является нижней унитреугольной. Компоненты ( tau_, tau_, ldots, tau_n ) — это множители Гаусса. Вектор ( tau^ ) называется вектором Гаусса.

Для реализации данных идей имеется функция, которая вычисляет вектор множителей. Если x — массив из n элементов и x[0] ненулевой, функция gauss возвращает вектор длины ( n-1 ), такой, что если M — матрица преобразования Гаусса, причем M[1:,1] = -gauss(x) и y = dot(M,x) , то y[1:] = 0 :

Применение матриц преобразовния Гаусса.

Умножение на матрицу преобразования Гаусса выполняется достаточно просто. Если матрица ( C in mathbb^ ) и ( M_k = I — tau^ e_k^T ), тогда преобразование вида $$ M_k C = (I — tau^ e_k^T)C = C — tau^ (e_k^T C) $$ осуществляет одноранговую модификацию. Кроме того, поскольку элементы вектора ( tau^ ) равны нулю от первого до ( k )-го равны нулю, то в каждой ( k )-ой строке матрицы ( C ) задействованы лишь элементы, начиная с ( k+1 )-го. Следовательно, если «C« — двумерный массив, задающий матрицу ( C ), и «M« задает ( n times n )-преобразование Гаусса ( M_1 ), причем «M[1:,1] = -t«, «t« — множитель Гаусса, соответствующий ( tau^ ), тогда следующая функция заменяет ( C ) на ( M_1C ):

Отметим, что если матрица M[k+1:,k] = -t , тогда обращение вида C[k. ] = gauss_app(C[k. ], t) заменяет ( C ) на ( M_kC )

Матрицы преобразовния Гаусса ( M_1, M_2, ldots, M_ ), как правило, можно подобрать так, что матрица ( M_M_ldots M_1A = U ) является верхней треугольной. Легко убедиться, что если ( M_k = I — tau^e_k^T ), тогда обратная к ней задается следующим выражением ( M_k^ = I + tau^ e_k^T ) и поэтому $$ begin tag A = LU, end $$ где $$ L = M_1^ M_2^ ldots M_^. $$

Очевидно, что ( L ) — это нижняя унитреугольная матрица. Разложение (3) называется ( LU )-разложением матрицы ( A ). Необходимо проверять ведущие элементы матрицы ( A ) (( a_ )) на нуль, чтобы избежать деления на нуль в функции gauss . Это говорит о том, что ( LU )-разложение может не существовать. Известно, что ( LU )-разложение матрицы ( A ) существует, если главные миноры матрицы ( A ) не равны нулю при этом оно единственно и ( det = u_ u_ cdots u_ ).

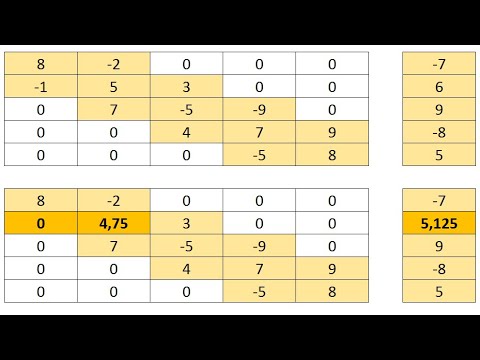
Рассмотрим пример при ( n=3 ):

Функция numpy.dot

Обратите внимание, что в приведенном примере мы использовали функцию dot модуля numpy , которая выполняет умножение матриц в «правильном смысле», в то время как выражение M1*A производит поэлементное умножение.

Обобщение этого примера позволяет представить ( k )-й шаг следующим образом:

• Мы имеем дело с матрицей ( A^ = M_cdots M_1A ), которая с ( 1 )-го по ( (k-1) )-й столбец является верхней треугольной.
• Поскольку мы уже получили нули в столбцах с ( 1 )-го по ( (k-1) )-й, то преобразование Гаусса можно применять только к столбцам с ( k )-го до ( n )-го. На самом деле нет необходимости применять преобразование Гаусса также и ( k )-му столбцу, так как мы знаем результат.
• Множители Гаусса, задающие матрицу ( M_k ) получаются по матрице ( A(k:n,k) ) и могут храниться в позициях, в которых получены нули.

С учетом сказанного выше мы можем написать следующую функцию:

Эта функция возвращает ( LU )-разложение матрицы ( A ). Где же храниться матрица ( L )? Дело в том, что если ( L = M_1^M_2^ ldots M_^ ), то элементы с ( (k+1) )-го до ( n )-го в ( k )-том столбце матрицы ( L ) равны множителям Гаусса ( tau_, tau_, ldots, tau_ ) соответственно. Этот факт очевиден, если посмотреть на произведение, задающее матрицу ( L ): $$ L = (I + tau^e_1^T cdots (I + tau^e_^T)) = I + sum_^ tau^e_k^T. $$ Поэтому элементы ( l_ = lu_ ) для всех ( i > k ). Здесь ( lu_ ) — элементы матрицы возвращаемой функцией lu .

После разложения матрицы ( A ) с помощью функции lu в возвращаемом массивы будут храниться матрицы ( L ) и ( U ). Поэтому мы можем решить систему ( Ax = b ), используя прямую и обратную подстановки описанные в разделе Треугольные системы:

Замечание

Отметим, что во всех представленных функциях мы выполняли явное преобразование входных параметров в массивы NumPy с элементами типа float . Это позволит правильно работать функциям в случае, если мы по ошибке создадим входные параметры не как массивы, а как списки.

Как известно метод Гаусса является прямым, т.е. дает точное решение системы линейных уравнений. Для проверки реализации решения системы линейных уравнений методом Гаусса мы можем написать следующую функцию:

Замечание

Здесь мы задали матрицу A системы и точное решение expected , на основе которых получили вектор правой части b = np.dot(A,x) . Для сравнения численного решения с точным используется функция np.linalg.norm . В случае вызова с одним аргументом вычисляется ( l_2 )-норма: ( | v |_2 = sqrt<sum_^n v_i^2> ).

Выбор ведущего элемента

Как уже упоминалось, ( LU )-разложение может не существовать. В методе Гаусса с выбором ведущего элемента на очередном шаге исключается неизвестное, при котором коэффициент по модулю является наибольшим. В этом случае метод Гаусса применим для любых невырожденных матриц (( det A ne 0 )).

Такая стратегия предполагает переупорядочивание данных в виде перестановки двух матричных строк. Для этого используются понятие перестановочной матрицы. Перестановочная матрица (или матрица перестановок) — это матрица, отличающаяся от единичной лишь перестановкой строк, например $$ P = begin 0 & 0 & 0 & 1\ 1 & 0 & 0 & 0\ 0 & 0 & 1 & 0\ 0 & 1 & 0 & 0 end. $$

Перестановочную матрицу нет необходимости хранить полностью. Гораздо более эффективно перестановочную матрицу можно представить в виде целочисленного вектора ( p ) длины ( n ). Один из возможных способов такого представления — это держать в ( p_k ) индекс столбца в ( k )-й строке, содержащий единственный элемент равный ( 1 ). Так вектор ( p = [4, 1, 3, 2] ) соответствует кодировке приведенной выше матрицы ( P ). Также возможно закодировать ( P ) указанием индекса строки в ( k )-ом столбце, содержащего ( 1 ), например, ( p = [2, 4, 3, 1] ).

Если ( P ) — это матрица перестановок, а ( A ) — некоторая матрица, тогда матрица ( AP ) является вариантом матрицы ( A ) с переставленными столбцами, а ( PA ) — вариантом матрицы ( A ) с переставленными строками.

Перестановочные матрицы ортогональны, и поэтому если ( P ) — перестановочная матрица, то ( P^ = P^T ).

В этом разделе особый интерес представляют взаимные перестановки. Такие перестановки осуществляют матрицы, получаемые простой переменой мест двух строк единичной матрицы, например $$ E = begin 0 & 0 & 0 & 1\ 0 & 1 & 0 & 0\ 0 & 0 & 1 & 0\ 1 & 0 & 0 & 0 end. $$

Взаимные перестановки могут использоваться для описания перестановок строк и столбцов матрицы. В приведенном примере порядка ( 4 times 4 ) матрица ( EA ) отличается от матрицы ( A ) перестановкой ( 1 )-й и ( 4 )-й строк. Аналогично матрица ( AE ) отличается от матрицы ( A ) перестановкой ( 1 )-го и ( 4 )-го столбцов.

Если ( P = E_n E_ cdots E_1 ) и каждая матрица ( E_k ) является единичной с переставленными ( k )-й и ( p_k )-й строками, то вектор ( p = [p_1, p_2, ldots, p_n] ) содержит всю необходимую информацию о матрице ( P ). Действительно, вектор ( x ) может быть замещен на вектор ( Px ) следующим образом: $$ begin mathbf & k = 1:n\ & x_k leftrightarrow x_

end $$ Здесь символ ( leftrightarrow ) обозначает «выполнение перестановки»: $$ x_k leftrightarrow x_

Leftrightarrow r = x_k, x_k = x_

, x_

= r. $$

Поскольку каждая матрица ( E_k ) является симметричной и ( P^T = E_1 E_2 cdots E_n ), то также можно выполнить замещение вектора ( x ) на вектор ( P^Tx ): $$ begin mathbf & k = n:1:-1\ & x_k leftrightarrow x_

end $$

Существуют разные стратегии выбора ведущего элемента. Мы остановимся на стратегии частичного выбора. Пусть матрица $$ A = begin 3 & 17 & 10 \ 2 & 4 & -2 \ 6 & 18 & -12 end. $$ Чтобы добиться наименьших множителей в первой матрице разложения по Гауссу с помощью взаимных перестановок строк, надо сделать элемент ( a_ ) наибольшим в первом столбце. Если ( E_1 ) — матрица взаимных перестановок, тогда $$ E_1 = begin 0 & 0 & 1 \ 0 & 1 & 0 \ 1 & 0 & 0 end. $$

Поэтому $$ E_1A = begin 6 & 18 & -12 \ 2 & 4 & -2 \ 3 & 17 & 10 end $$ и $$ M_1 = begin 1 & 0 & 0 \ -1/3 & 1 & 0 \ -1/2 & 0 & 1 end Rightarrow M_1E_1A = begin 6 & 18 & -12 \ 0 & -2 & 2 \ 0 & 8 & 16 end. $$

Теперь, чтобы получить наименьший множитель в матрице ( M_2 ), необходимо переставить ( 2 )-ю и ( 3 )-ю строки и т.д.

Пример иллюстрирует общую идею, основанную на перестановке строк. Обобщая эту идею, получим следующий алгоритм:

( LU )-разложение с частичным выбором

Если матрица ( E in mathbb^ ), то данный алгоритм вычисляет матрицы преобразования Гаусса ( M_1, M_2 ldots, M_ ) и матрицы взаимных перестановок ( E_1, E_2, ldots, E_ ), такие что матрица ( M_E_ cdots M_1E_1A = U ) является верхней треугольной. При этом нет множителей, превосходящих ( 1 ) по абсолютной величине. Подматрица ( [a_]_^k ) замещается на матрицу ( [u_]_^k ), ( k = 1, 2, ldots, n ). Подматрица ( [a_]_^n ) замещается на матрицу ( [m_]_^ ), ( k = 1, 2, ldots , n-1 ). Целочисленный вектор ( piv ) размера ( n-1 ) задает взаимные перестановки. В частности, матрица ( E_k ) переставляет строки ( k ) и ( piv_k ), ( k = 1, 2, ldots, n-1 ).

for ( k = 1:n )

1. Зададим ( mu ), такое что ( k leq mu leq n ) и ( |a_| = max_|a_| )
2. ( a_ leftrightarrow a_ ); ( piv_k = mu )

if ( a_ ne 0 )

Чтобы решить линейную систему ( Ax = b ) после вызова последнего алгоритма, мы должны

1. Вычислить вектор ( y = M_E_ cdots M_1E_1 b ). 2. Решить верхнюю треугольную систему ( Ux = y ).

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Линейная алгебра — программируем с Numpy(ч .2)

Здравствуйте. Сегодня речь пойдёт об очень интересных вещах, поэтому не вижу надобности задерживать ваше внимание. Продолжаем изучать линейную алгебру и сразу переходим к минорам.

Миноры порядка k

Дана матрица размером .

Def. Зафиксируем : и столбцов: . Определитель матрицы, которая является пересечением выбранных строк и столбцов называется минором порядка : .

Пример.

Минор, который является определителем матрицы, состоящей из пересечения всех остальных строк и столбцов, является дополняющей минором минором.

Def. Алгебраическим дополнением минора называют

Теорема Лапласа

Th Лапласа. Фиксируем строк матрицы. Тогда определитель этой матрицы равен сумме всех возможных произведений миноров порядка на этих строках с их алгебраическими дополнениями.

Пример.

Метод Гаусса вычисления определителя

Последней темой, которую мы затронем в этой статье, станет метод Гаусса вычисления определителя.

Основной идеей, которую нам следует запомнить, является тот факт, что определитель треугольной матрицы равен произведению элементов главной диагонали.

Сразу стоит отметить, что если , то определитель матрицы равен нулю. Далее мы производим следующую операцию:

1)]» title=»Rendered by QuickLaTeX.com»/>

В следствии, становится равен нулю. Таким же образом далее выполняем операцию для 2″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»38″ style=»vertical-align: -2px;»/>, только вместо выбираем . Если же равен нулю, мы меняем местами строки и меняем знак определителя.

После выполнения необходимого кол-ва итераций мы получаем треугольную матрицу, вычисление определителя которой не вызывает ровно никаких трудностей.

Пример.

Программируем на Python

Реализуем функционал вычисления определителя квадратной матрицы, используя Python.

Разберём, что поэтапно выполняется в функции. Сначала мы копируем исходную матрицу и приводим её к типу ‘float32’ . Далее следует проверка, является ли матрица квадратной. После мы выполняем алгоритм, при чём при при смене строк местами меняем знак определителя.

После нам остается всего лишь вычислить произведение элементов главной диагонали и выбрать корректный знак.

Протестируем на матрице из примера выше.

Всё работает прекрасно. На этом наш очередной шаг в мир линейной алгебры подходит к концу.

Заключение

Сегодня мы разобрали такие понятия из раздела «Линейная алгебра», как минор, алгебраическое дополнение и метод Гаусса вычисления определителя квадратной матрицы. Далее на изучение следует ещё очень много вещей, и со всем мы разберёмся.

Советую прочитать статью про нашу авторскую разработку: «Анализ данных групп во Вконтакте»,

А также подписывайтесь на группу ВКонтакте, Telegram и YouTube-канал. Там еще больше полезного и интересного для программистов.

🌟 Видео

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Решение систем линейных матричных уравнений через формулы Крамера в PythonСкачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Решение системы уравнений методом Гаусса 4x4Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Математика это не ИсламСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Решения системы линейных уравнений на Python (Sympy).Скачать

Метод Гаусса решения систем линейных уравненийСкачать

VB.net Vs С++. СЛАУ Метод ГауссаСкачать