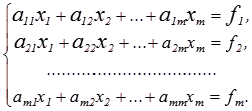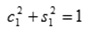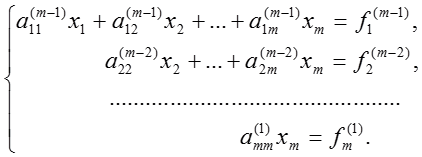Решение системы линейных алгебраических уравнений методом вращений

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Г. И. НОСОВА»

Кафедра вычислительной техники и прикладной математики

по дисциплине: «Вычислительная математика»

на тему: «Метод вращений решения СЛАУ»

Исполнитель: Сысоев Н.В,, студент 2 курса, АВ-09-1.

Руководитель: Филиппов Е. Г.

1 Теоретический обзор

1.1 Прямые методы

1.2 Метод Гаусса

1.2.1 Описание метода

1.2.2 Сходимость метода простой итерации

1.2.3 Апостериорная оценка погрешности

1.3 Метод вращений линейных систем

1.3.1 Описание метода

1.3.2 Контроль точности и уточнение приближенного решения в рамках прямого метода

1.3.3 Апостериорная оценка погрешности

1.4 Метод релаксации

2 Практическая часть

2.1 Таблица идентификаторов

2.2 Листинг программы

2.4 Сравнительная таблица

Как утверждается в книге известного американского математика Валяха, 75% всех расчетных математических задач приходится на решение СЛАУ. Это не удивительно, так как математические модели тех или иных явлений или процессов либо сразу строятся как линейные алгебраические, либо сводятся к таковым посредством дискретизации и/или линеаризации. Поэтому трудно переоценить роль, которую играет выбор эффективного способа решения СЛАУ. Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ – многими пакетами прикладных программ, позволяющих решать различные возникающие на практике линейные системы. Чтобы ориентироваться среди методов и программ и в нужный момент сделать оптимальный выбор нужно разбираться в основе построений методов и алгоритмов, учитывающих специфику постановок задач, знать их сильные и слабые стороны и границы применимости.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

1 Теоретический обзор

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

1.1 Прямые методы

математический модель итерация погрешность

Все методы решения линейных алгебраических задач можно разбить на два класса: прямые и итерационные. Прямые методы – это такие методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (в связи с чем к классу прямых методов применяют название точные методы). Итерационные методы – это методы в которых точное решение может быть получено лишь в результате бесконечного повторения единообразных действий.

Эффективность способов решения системы

или

иначе, векторно-матричных уравнений Ах=f, где f=(f1, f2, …,fn)T – вектор свободных членов и

х=( х1, х2, …,хn)T – вектор неизвестных, а – вещественная n×n-матрица коэффициентов данной системы, во многом зависит от структуры и свойств матрицы А : размера, обусловленности, симметричности, заполненности и др.

Так размерность системы (т.е число n) является главным фактором, заставляющим вычислителей отвернуться от весьма привлекательных в теоретическом плане и приемлемых на практике при небольших n формул Крамера.

Видео:Решение системы уравнений методом Крамера.Скачать

1.2 Метод Гаусса

1.2.1 Описание метода

Рассмотрим один из самых распространенных методов решения СЛАУ – метод Гаусса. Этот метод (который называют также методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым ходом и обратным ходом. Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы (1):

для преобразования её к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.

1.2.2 Алгоритм.

1.2.3 Апостериорная оценка погрешности.

1.2.4 Пример

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

1.3 Метод вращений линейных систем

1.3.1 Описание метода.

Как и в методе Гаусса, цель прямого хода преобразований в этом методе – приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.

Пусть с1 и s1 – некоторые отличные от нуля числа. Умножим первое уравнение исходной системы (1) на с1, второе на s1 и сложим их; полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножаем на –s1, второе – на c1 и результатом их сложения заменим второе уравнение. Таким образом, первые два уравнения (1) заменяются уравнениями

Отсюда .

Эти числа можно интерпретировать как косинус и синус некоторого угла (отсюда название метод вращений, каждый шаг такого преобразования можно рассматривать как вращение расширенной матрицы системы в плоскости обнуляемого индекса).

В результате преобразований получим систему

Далее первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений соотведлтственно на

а третье – уравнением, полученным при сложении результатов умножения тех же уравнений соответственно на –s2 и с2. Получим систему

Выполнив преобразование m-1 раз, придем к системе

Вид полученной системы такой же, как после первого этапа преобразований методом Гаусса. Эта система обладает следующим свойством: длина любого вектора-столбца (эвклидова норма) расширенной матрицы остается такой же, как у исходной матрицы. Следовательно, при выполнении преобразований не наблюдается рост элементов.

Далее по этому же алгоритму преобразуется матрица

В результате m-1 этапов прямого хода система будет приведена к треугольному виду.

Нахождение неизвестных не отличается от обратного хода метода Гаусса.

Треугольная, точнее, трапециевидная структура последней системы позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего:

1.3.2 Контроль точности и уточнение приближенного решения в рамках прямого метода

Прямые методы часто приводят к точному решению СЛАУ при точном выполнении предусматриваемых соответствующими алгоритмами арифметических операций (без округлений).

Реальные же вычисления базируются на арифметике машинных (т.е. усеченных до определенного количества разрядов) чисел. Как отражается на результате решения системы подмена арифметики действительных чисел машинной арифметикой, зависит от самой решаемой системы, параметров применяемого компьютера и системы представления данных, способов реализации алгоритмов. В любом случае, практически вместо точного решения СЛАУ прямой метод дает приближенное решение*) (обозначим его х(0)). Подставив х(0) в выражение ξ:=f-Ax, называемое невязкой, по малости полученного вектора значения ξ(0)=f-Ax(0) можно с осторожностью судить о близости найденого решения x(0) к точному решению x. Если, напимер,

|| ξ(0)|| — недостаточно малая величина, то следует искать вектор-поправку p такой, что x(0)+р=х есть точное решение системы

т.е. А(х(0)+р)=f.

Последнее равносильно векторно матричному уравнению

Таким образом, нахождение поправки сводится к решению такой же системы, как и

,

где в качестве вектора свободных членов должен быть взят вектор невязок.

1.3.3 Апостериорная оценка погрешности.

1.3.4 Пример

Видео:Решение системы уравнений методом ГауссаСкачать

1.4 Метод релаксации

1.4.1 Пример

Видео:Решение системы уравнений методом Крамера 2x2Скачать

2 Практическая часть

Видео:Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

2.1 Таблица идентификаторов

Видео:Решение системы уравнений методом обратной матрицы.Скачать

2.2 Листинг программы

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

2.3 Пример.

Подсчитаем матрицу неизвестных(Otvet1) и матрицу поправок(Otvet2)

Для сравнения, погрешность метода Гаусса:

Таким образом, можно говорить о том, что, действительно, метод вращений более точен.

Видео:Матричный метод решения систем уравненийСкачать

2.4 Сравнительная таблица

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Заключение

В данной работе был рассмотрен метод релаксации решения систем линейных алгебраических уравнений. Была подробно рассмотрена теоретическая часть, из которой выводятся различные формулы для реализации данного метода. А также было выполнено сравнение метода релаксации с методами простой итерации и Зейделя. Программная реализация выше описанных методов представлена в приложении А.

По результатам работы можно сделать следующие выводы. Во-первых, скорость сходимости метода релаксации превышает скорости сходимости методов простой итерации и Зейделя. Во-вторых, скорость сходимости напрямую зависит от выбора параметра релаксации. Таким образом, данный метод удобен для решения СЛАУ средней размерности.

Еще одно достоинство итерационного метода верхних релаксаций состоит в том, что при его реализации на ЭВМ алгоритм вычислений имеет простой вид и позволяет использовать всего один массив для неизвестного вектора.

Видео:Решение систем уравнений методом сложенияСкачать

Библиографический список

1) Вержбицкий В. М. Основы численных методов: Учеб. пособие для вузов / В. М. Вержбицкий. — М. : Высш. шк. , 2002. — 840 с.

2) И.Г. Серебренникова, Г.М. Коринченко, Вычислительная математика. МГТУ им Г.И. Носова 2003г. 146с

3) Е. Волков.Численные методы. М.,1987, 248 с.

4) А. И. Плис, Н. А. Сливина. Лабораторный практикум по высшей математике. — М.: «Высшая школа», 1983.

5) Калиткин Н.Н. Численные методы. М.: Наука, 1978, 512 с.

6) Демидович Б.П., Марон И.А. Основы вычислительной математики. -М.: Наука, 1966 г., 664 стр.

7) Фадеев Д.К., Фадеева В.Н. Вычислительные методы линейной алгебры. М. Физматлит, 1960.

8) Воеводин В.В. Вычислительные основы линейной алгебры. — М.: Наука, 1977. — 304 с.

9) А. Самарский. Введение в численные методы. М.,1988, 270 с.

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Линейные уравнения. Решение систем линейных уравнений. Метод вращения.

Метод вращений. Как и в методе Гаусса, целью прямого хода преобразований в методе вращений является приведение системы линейных уравнений к треугольному виду методичным обнулением поддиагональных элементов сначала 1-го столбца, далее 2-го и так далее.

Допустим с₁ и s₁ – ненулевые числа. Умножаем 1-е уравнение системы на с₁, 2-е на s₁ и складываем их; уравнением, которое мы получили, заменяем 1-е уравнение системы. Далее 1-е уравнение начальной системы нужно умножить на – s₁, 2-е – на c₁ и итогом этого заменяем 2-е уравнение. Т.о., первые 2 уравнения заменяем уравнениями:

— условие исключения х₁ из второго уравнения и

Эти числа можно истолковать как cos и sin некоторого угла α₁ (поэтому метод так и называется — все шаги этого преобразования рассматриваются как вращение расширенной матрицы системы в плоскости индекса, который обнуляется).

После преобразований получаем систему:

Теперь 1-е уравнение системы заменяем полученным, результатом сложения итогов умножения 1-го и 3-го уравнений соответственно на:

а 3-е – уравнением, которое получим после сложения результатов умножения уравнений соответственно на – s₂ и с₂. Получаем систему:

Выполняя преобразование m-1 раз, приходим к системе:

Вид системы, которую мы получили, такой же, как и после 1-го этапа преобразований методом Гаусса. У этой системы следующие свойства: длина всех векторов-столбцов расширенной матрицы остается такая же, как у исходной матрицы. То есть, при выполнении преобразований не роста элементов нет.

Далее, по этому же алгоритму преобразуем матрицу:

В итоге m-1 этапов прямого хода система приведется к треугольному виду:

Определение неизвестных такое же как и в обратном ходе метода Гаусса.

Треугольная, или, трапециевидная структура последней системы дает нам поочередно 1 за другим вычислить значения неизвестных, начиная с последнего:

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Метод вращений

Одним из эффективных методов, позволяющих привести исходную симметрическую матрицу n-го порядка к трехдиагональному виду, является метод вращений. Он основан на специально подбираемом вращении системы координат в n-мерном пространстве. Поскольку любое вращение можно заменить последовательностью элементарных (плоских) вращений, то решение задачи можно разбить на ряд шагов, на каждом из которых осуществляется плоское вращение. Таким образом, на каждом шаге выбираются две оси – i-я и j-я (i≠ j),и поворот на угол φ производится в плоскости, проходящей через эти оси; остальные оси координат на данном шаге неподвижны. Матрица вращения при этом имеет вид

(3.8)

Здесь мы рассматриваем матрицы с вещественными элементами. В случае комплексных векторов для использования этого метода нужно изменить формулы (3.8).

Для осуществления преобразования подобия (3.7) необходимо найти обратную матрицу . Можно показать, что она равна в рассматриваемом случае транспонированной матрице . Для получения обратной матрицы достаточно провести зеркальное отражение всех элементов исходной матрицы относительно ее диагонали. Другими словами, нужно поменять местами строки и столбцы исходной матрицы; элементы pijи pjiпри этом поменяются местами.

Угол поворота φ на каждом шаге выбирают таким, чтобы в преобразованной матрице обратился в нуль один элемент (в симметрической матрице – два). Процесс преобразования исходной матрицы путем элементарного вращения на любом k—мшаге можно представить в виде рекуррентных соотношений:

(3.9)

Здесь матрицы вращений Р и значения i,jзависят от номера шага k.

Рассмотрим первый шаг преобразования. Сначала вычисляют произведение матриц (здесь А(0) – исходная матрица А).Как видно из (3.8), в полученной матрице отличными от исходных являются элементы, стоящие в i-м и j—мстолбцах; остальные элементы совпадают с элементами матрицы A(0) т.е.

(3.10)

Затем находят преобразованную матрицу . Элементы полученной матрицы отличаются от элементов матрицы В только i-й и j—йстроками. Они связаны соотношениями:

(3.11)

Таким образом, преобразованная матрица отличается от элементами строк и столбцов с номерами iи j. Эти элементы пересчитывают по формулам (3.10), (3.11). В данных формулах пока не определенными остались параметры р и q; при этом лишь один из них свободный, поскольку они подчиняются тождеству:

(3.12)

Недостающее одно уравнение для определения этих параметров получают из условия обращения в нуль некоторого элемента новой матрицы А(1)В зависимости от выбора этого элемента строят различные алгоритмы метода вращений.

Одним из таких алгоритмов является последовательное обращение в нуль всех ненулевых элементов, лежащих вне трех диагоналей исходной симметрической матрицы. Это так называемый прямой метод вращений. В соответствии с этим методом обращение в нуль элементов матрицы осуществляют последовательно, начиная с элементов первой строки (и первого столбца, так как матрица симметрическая).

Процесс вычислений поясним с использованием схематического изображения матрицы (рис. 3.1). Точками отмечены элементы матрицы. Наклонные линии указывают три диагонали матрицы, элементы на которых после окончания расчета отличны от нуля. Алгоритм решения задачи нужно построить таким образом, чтобы все элементы по одну сторону от этих трех диагоналей обратились в нуль; тогда симметрично расположенные элементы также станут нулевыми. Обращение элементов в нуль можно выполнять, например, в следующей последовательности: a13, a14, … , a1n, a24, a25, …, a2n, …, an-2, n.

Рассмотрим сначала первый шаг данного метода, состоящий в обращении в нуль элемента а13 (и автоматически a31). Для осуществления элементарного вращения нужно выбрать две оси — i-ю и j—ю,так чтобы элемент а13 оказался в строке или столбце с номером i или j. Положим i = 2, j= 3 и умножим матрицу А(0)справа на матрицу вращения Р23 и слева на транспонированную матрицу Р23T. Получим новые значения элементов матрицы, которые вычисляем по формулам (3.10), (3.11). Полагая в них l=1 и т = 3, находим

Учитывая тождество (3.12), получаем систему уравнений для определения параметров р, q:

Рис. 3.1. Схематическое изображение матрицы к иллюстрации метода вращений

Решая эту систему, находим

Используя эти параметры р, q, можно по формулам (3.10), (3.11) вычислить значения элементов, стоящих в строках и столбцах с номерами i — 2, 3; j — 2, 3(остальные элементы исходной матрицы не изменились).

Аналогично, выбирая для элементарного вращения i-ю и j-ю оси, можно добиться нулевого значения любого элемента на k—мшаге. В этом случае строят матрицу вращения Рij, параметры которой вычисляют по формулам, полученным из условия равенства нулю элемента и (3.12). Эти формулы имеют вид

С учетом найденных значений параметров р, qможно по формулам (3.10), (3.11) найти элементы преобразованной матрицы. Для иллюстрации вновь обратимся к рис. 3.1. Вертикальными линиями показаны столбцы с номерами iи j, соответствующими осям элементарного вращения, горизонтальными – строки с теми же номерами. На рассматриваемом шаге матрица преобразуется таким образом, чтобы отмеченные крестиками элементы обратились в нуль. Элементарное вращение (3.9) на каждом шаге требует пересчета всех элементов отмеченных столбцов и строк. С учетом симметрии можно вычислить лишь все элементы столбцов, а элементы получаются из условий симметрии. Исключение составляют лишь элементы, расположенные на пересечениях этих строк и столбцов. Они изменяются на каждом из двух этапов выполняемого шага.

Таким образом, на каждом шаге преобразования симметрической матрицы для вычисления элементов столбцов используют формулы (3.10), а элементы, находящиеся на пересечениях изменяемых строк и столбцов, пересчитывают еще по формулам (3.11). При этом полученные ранее нулевые элементы не изменяются. Алгоритм приведения симметрической матрицы к трехдиагональному виду с помощью прямого метода вращений представлен на рис. 3.2.

Рис. 3.2. Алгоритм приведения симметрической матрицы к трехдиагональному виду с помощью прямого метода вращений

Собственные значения полученной трехдиагональной матрицы будут также собственными значениями исходной матрицы. Собственные векторы xi исходной матрицы не равны непосредственно собственным векторам yiтрехдиагональной матрицы, а вычисляют их с помощью соотношений

💡 Видео

Решение системы трех уравнений по формулам КрамераСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение системы уравнений методом Гаусса 4x4Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать