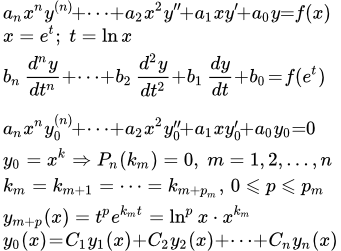Решение системы дифференциальных уравнений методом эйлера комплексные корни

Видео:Системы дифференциальных уравнений.Метод исключения.Метод Эйлера.Скачать

Интегрирование однородных линейных систем ДУ
с постоянными коэффициентами. Метод Эйлера

Линейной однородной системой с постоянными коэффициентами называется система дифференциальных уравнений вида

где коэффициенты — постоянные, а — искомые функции от .

Систему (1) можно коротко записать в виде одного матричного уравнения

называется частным решением уравнения (2) в интервале , если выполняется тождество

Система частных решений

(здесь в записи нижний индекс указывает номер решения, а верхний — номер функции в решении) называется фундаментальной на интервале , если ее определитель Вронского

Теорема. Если система частных решений однородного уравнения (2) является фундаментальной, то общее решение этого уравнения имеет вид

где — произвольные постоянные.

Линейные системы можно интегрировать различными способами, рассмотренными ранее, например методом исключения, путем нахождения интегрируемых комбинаций и т.д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также метод Эйлера .

Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:

Решение системы (3) ищем в виде

Подставляя (4) в (3) и сокращая на , получаем систему уравнений для определения и

Система (5) имеет ненулевое решение, когда ее определитель равен нулю,

Уравнение (6) называется характеристическим .

А. Пусть корни и характеристического уравнения — вещественные и различные . Подставив в (5) вместо число и решив систему (5), получим числа и . Затем положим в (5) и получим числа и, наконец, при получим и . Соответственно трем наборам чисел и получим три частных решения

Общее решение системы (3) имеет вид

Пример 1. Решить систему дифференциальных уравнений

Решение. Составляем характеристическое уравнение

Корням соответствуют числа

Выписываем частные решения

Общее решение системы:

Б. Рассмотрим теперь случай, когда корни характеристического уравнения комплексные .

Пример 2. Решить систему линейных однородных дифференциальных уравнений

Решение. Выпишем систему для определения и

имеет корни . Подставляя в (8), получаем два уравнения для определения и

из которых одно является следствием другого (в силу того, что определитель системы (8) равен нулю).

Возьмем , тогда первое частное решение запишется так:

Аналогично, подставляя в (8) корень , найдем второе частное решение:

Перейдем к новой фундаментальной системе решений:

Пользуясь известной формулой Эйлера , из (9), (10) и (11) получаем

Общим решением системы (7) будет

Замечание. Найдя первое частное решение (9), можно было бы сразу написать общее решение системы (7), пользуясь формулами

где и обозначают соответственно действительную и мнимую части комплексного числа , т. е. если , то , .

В. Случай кратных корней.

Пример 3. Решить систему

Решение. Характеристическое уравнение

Решение следует искать в виде

Подставляя (13) в первое уравнение системы (12), получаем

Приравнивая коэффициенты при одинаковых степенях в левой и правой части (14), получаем:

Величины и остаются произвольными. Обозначая их соответственно через и , получаем общее решение системы (12):

Замечание. Легко проверить, что если (13) подставить во второе уравнение системы (12), то получим тот же результат (15). В самом деле, из равенства

получаем два соотношения для определения и через и

Пример 4. Решить задачу Коши для системы линейных дифференциальных уравнений

с начальными условиями .

Решение. Характеристическое уравнение

Корни уравнения (17): . Действительному корню отвечает решение

Подставляя (18) в систему (16) и сокращая на , получаем

откуда . Полагаем, например, , тогда и частное решение (18):

Комплексному корню отвечает решение

подставив которое в (16) и сокращая на , получим

откуда , так что, например, при имеем и частное решение

Корню соответствует решение, комплексно сопряженное решению (20), т.е.

Учитывая (19), (20), (21), получаем общее решение

Выделим, наконец, решение с начальными условиями . Из (22) при имеем

Воспользовавшись формулами Эйлера , окончательно получим

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение системы дифференциальных уравнений методом эйлера комплексные корни

Системой дифференциальных уравнений называется система вида

где x — независимый аргумент,

y_i — зависимая функция, ,

Функции y_i(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.

Численные методы решения систем дифференциальных уравнений.

Модифицированный метод Эйлера.

Метод Рунге-Кутта четвертого порядка.

Дифференциальным уравнением второго порядка называется уравнение вида

Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Численно ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.

Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводится к машинному виду (3). Для этого вводится новая неизвестная функция , слева в каждом уравнении системы оставляют только первые производные неизвестных функций, а в правых частях производных быть не должно

.

(3)

Функция f₂(x, y₁, y) в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид. Для решения системы из n уравнений расчетные формулы приведены выше. Для решения системы из двух уравнений расчетные формулы удобно записать без двойных индексов в следующем виде:

Метод Рунге-Кутта четвертого порядка.

где h — шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x₀, y₁=y₁₀, y=y₀.

Контрольное задание по зачетной работе.

Колебания с одной степенью свободы

Цель. Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.

Задание. Численно и аналитически найти:

1. закон движения материальной точки на пружинке х(t),
2. закон изменения силы тока I(t) в колебательном контуре (RLC — цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.

Свободные незатухающие колебания

Затухающее колебательное движение

Предельное апериодическое движение

Вынужденное колебание без сопротивления

Вынужденное колебание без сопротивления, явление резонанса

Вынужденное колебание с линейным сопротивлением

Вынужденное колебание с линейным сопротивлением, явление резонанса

Видео:Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Видео:Метод ЭйлераСкачать

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

🔥 Видео

Метод Эйлера. Решение систем ДУСкачать

МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

ДУ Линейные системыСкачать

Системы дифференциальных уравнений. Метод Эйлера.Скачать

Система неоднородных дифференциальных уравненийСкачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Систем линейных дифференциальных уравненийСкачать

Численное решение задачи Коши методом ЭйлераСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 5Скачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Линейные системы дифференциальных уравнений с постоянными коэффициентамиСкачать