Решение системы дифференциальных уравнений excel (8 видео)

Обзор методов решения в Excel

Введение

Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

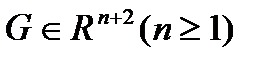
Решением этого уравнения на интервале I=[a,b] называется функция u(x).

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k_-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)

Обзор методов решения в Excel

1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка

Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

Содержание

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Сдвижков О.А.
Похожие темы научных работ по математике , автор научной работы — Сдвижков О.А.
EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM
Текст научной работы на тему «ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА»
Решение системы уравнений в Microsoft Excel
Варианты решений
Способ 1: матричный метод
Способ 2: подбор параметров
Способ 3: метод Крамера
Способ 4: метод Гаусса
📹 Видео

Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА Текст научной статьи по специальности « Математика»

Видео:Решение системы уравнений в ExcelСкачать

Аннотация научной статьи по математике, автор научной работы — Сдвижков О.А.

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1-го порядка и отдельных дифференциальных уравнений 1-го порядка.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

The current study presents program codes of custom VBA Excel functions that implement numerical methods for solving the Cauchy problem for a system of 1st order ordinary differential equations using the Euler and Runge-Kutta 4th order methods. The parameters of the functions are the initial and final values of the independent variable, an array of initial values of the dependent variables, and the number of steps. Program codes use dynamic arrays. Custom functions can be applied to the Cauchy problem and one of the 1st order differential equations. All of the custom functions have descriptions that explain their purpose. The article demonstrates the use of custom functions using specific examples of numerical solutions to the Cauchy problem of 1st order differential equations system and individual 1st-order differential equations.

Видео:Решение системы уравнений с двумя неизвестными помощью ExcelСкачать

Текст научной работы на тему «ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА»

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА

Российский государственный университет туризма и сервиса, Пушкино МО, Россия * Корреспондирующий автор (oasdv[at]yandex.ru)

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1 -го порядка и отдельных дифференциальных уравнений 1 -го порядка.

Ключевые слова: система дифференциальных уравнений, задача Коши, численные методы, код, диалоговое окно.

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

Russian State University of Tourism and Service, Pushkino, Moscow Oblast, Russia * Corresponding author (oasdv[at]yandex.ru)

Keywords: system of differential equations, Cauchy problem, numerical methods, code, dialog box.

Системы обыкновенных дифференциальных уравнений 1-го порядка имеют большое прикладное значение [9]. Однако численные методы решения задачи Коши системы обыкновенных дифференциальных уравнений 1 -го порядка отличаются большой трудоемкостью [1], [2], [6]. Поэтому задача информатизации этих методов, доступной самому широкому кругу пользователей ПК, каким является круг пользователей Microsoft Office, несомненно, является актуальной.

Цель данного исследования — разработка на языке программирования VBA Excel [3], [4], [7] программных кодов пользовательских функций [10], которыми численно решается задача Коши системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта.

Программный код функции VBA Excel для решения методом Рунге-Кутта системы двух дифференциальных уравнений приведен в [5]. Пользовательские функции VBA Excel для численного решения задачи Коши обыкновенного дифференциального уравнения 1-го порядка приведены в [9].

1. Пользовательская функция ЭЙЛЕР

В методе Эйлера численного решения задачи Коши системы дифференциальных уравнений

dyL = f1(Х У1, У 2 Ут ) ах

= Л(Х У1, У 2 Ут ) „ 1Ч

йУт = /т (Х У1, У2 Ут )

У1( Хо) = У°, У2(Хо) = У20,-, Ут (Хо) = У0т (1.2)

на отрезке [хо, xo + n h] применяется формула:

у л = У ji-1 + h • f (хо + (i — 1)h Уи-1> У 2 i-iv, Ут1-1) (1.3)

j = 1, 2, . m; i= 1, 2, . n.

Правые части системы (1.1) в VBA Excel можно задать пользовательской функцией СИСТЕМ, листинг которой имеет вид:

Function СИСТЕМ (Массив As Variant)

‘массив состоит из значений^ — номера уравнения,х,у1,у2. yn Select Case Массив(1) Case 1

СИСТЕМ = /1(Массив(2), Массив(3), . Массив(т)) Case 2

СИСТЕМ = /2(Массив(2), Массив(3), . Массив(т))

СИСТЕМ = /п(Массив(2), Массив(3), . Массив(т)) End Select End Function

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция ЭЙЛЕР, код VBA Excel которой приведен в листинге 1, выполняет вычисления по формуле (1.3). Листинг 1. Код функции ЭЙЛЕР и ее описания Function ЭйЛЕР(Нач_х0, Конеч_х, Нач_у0(), Шагов) As Variant Dim n As Integer, m As Integer, x(), y(), z(), c() n = Шагов:т = иВоиМ(Нач_у0) ReDim z(1 To m, 0 To n):ReDim x(0 To n) ReDim y(1 To m + 2):ReDim c(1 To m) x(0) = Нач_x0:h = (Конеч_x — x(0)) / n For i = 1 To m z(i, 0) = Нач_у0® Next

Forj = 1 To n For i = 1 To m

y(1) = i: y(2) = x(0) + h * (j — 1) For r = 3 To m + 2 y(r) = z(r — 2, j — 1) Next

z(i, j) = z(i, j — 1) + h * СИСТЕМ(Массив)

For i = 1 To m c(i) = z(i, n) Next

ЭЙЛЕР = c End Function Sub InstallFunc2()

Application.MacroOptions Macш:=»ЭИЛЕР», Descriptions _ «Возвращает значения yi, полученные методом Эйлера» End Sub

В листинг 1 входят массивы:

z(1 To m, 0 To n)- двумерный массив значений функцийу1, у2, . ym в точках x0, x0+h, . x0+n h; x(0 To n) — массив значений х0, x0+h, . x0+nh;

y(1 To m + 2) — массив значений (i, x, y1, y2, . ym), где i — номер уравнения системы;

c(1 To m) — массив итоговых значений массива z.

Пример 1.1. Найти приближенные значения решения системы

с начальными условиями у (0) = 0, у2(0) = 1. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant)

Select Case Массив (1) Case 1

СИСТЕМ = Массив (4) Case 2

СИСТЕМ = Массив (3) End Select End Function

2. В диапазон А1:А5 вводятся значения, принимаемые переменной х: 0; 0,1; 0,2; 0,3; 0,4.

3. В диапазон В1:С1 вводятся начальные значения, принимаемые у1 и у2: 0 и 1.

4. Выделяется диапазон В2:С2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.1 — Применение функции ЭЙЛЕР в примере 1.1

5. Команда Ог^Ый +Enter возвращает в диапазоне В2:С2 результаты.

6. Копирование данных диапазона В2:С2 в диапазон В3:С5 завершает решение задачи (рис. 1.2).

Рис. 1.2 — Вид решения примера 1.1 функцией ЭЙЛЕР Пример 1.2. Найти приближенные значения решения системы

с начальными условиями у (0) = 1, у2(0) = 2, у3 (0) = 3. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4; 0,5.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant) Select Case Массив(1) Case 1

СИСТЕМ = Массив(4) + Массив(5) Case 2

СИСТЕМ = Массив(3) + Массив(5) Case 3

СИСТЕМ = Массив(3) + Массив(4)

End Select End Function

2. В диапазон А1:А6 вводятся значения, принимаемые х: 0; 0,1; 0,2; 0,3; 0,4; 0,5.

3. В диапазон B1:D1 вводятся начальные значения, принимаемые yi, у2, у3: 1, 2, 3.

4. Выделяется диапазон B2:D2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.3 — Применение функции ЭЙЛЕР в примере 1.2

5. Команда Ог1+8Ый +Бйег возвращает в диапазоне В2:Б2 результаты.

6. Копирование данных диапазона В2:Б2 в диапазон В3:Б6 завершает решение задачи (рис. 1.4).

J 0,2 2,07 2,88 3,69

4 0,3 2,727 3,456 4,185

5 0,4 3,4911 4,1472 4,8033

Б 0,5 4,38615 4,97664 15,56713

Рис. 1.4 — Вид решения примера 1.2 функцией ЭЙЛЕР

Функция Эйлер применима и к задаче Коши обыкновенного дифференциального уравнения 1 -го порядка. Пример 1.3. Найти приближенные значения решения задачи Коши

на отрезке [0, 1], разбивая отрезок на 10 равных частей. В этом случае код функции СИСТЕМ имеет вид: Function СИСТЕМ(Массив As Variant) СИСТЕМ = Массив(2) + Массив(3) End Function

Применение функции ЭЙЛЕР приводит к результатам, показанным на рисунке 1.3.

В с D Е F G Н 1 J К

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

1,1 1,22 1,362 1,5282 1,72102 1,943122 2,197434 2,487178 2,815895 3,187485]

Рис. 1.5 — Вид решения примера 1.3 функцией ЭЙЛЕР

2. Пользовательская функция РУНГЕ

В методе Рунге-Кутта четвертого порядка точности, которым численно решается задача Коши (1.1, 1.2):

k(2) = fj (x. + h / 2, уи + h ■ С / 2. уш + h • k« /2), (2.2)

k(? = fj (x + h /2, yH + h ■ k^ / 2. у„г + h ■ кП2) / 2), k(4 = fj(x + h,yw + h ■ *£>. уйг + h ■ О.

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция РУНГЕ, программный код VBA Excel которой приведен в листинге 2, выполняет вычисления по формулам (2.1), (2.2). Листинг 2. Код функции РУНГЕ и ее описания Function РУНГЕ(Нач_х, Конеч_х, Нач_у() As Variant, Шагов) _ As Variant

Dim n As Integer, m As Integer, h As Single, x(), y(), z(), c()

n = Шагов:т = иВоиМ(Нач_у)

ReDim z(1 To m, 0 To n):ReDim x(0 To n)

ReDim y(l To m + 2):ReDim c(1 To m)

Dim K(1 To 4) As Double

x(0) = Нач_x:h = (Конеч_х — x(0)) / n

For i = 1 To n Forj = 1 To m

y(1) = j: y(2) = x(0) + h * (i — 1) For r = 3 To m + 2 y(r) = z(r — 2, i — 1) Next

Массив = y:K(1) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(1) / 2 Next

K(2) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(2) / 2 Next

K(3) = h * СИСТЕМ(Массив):y(1) = j: y(2) = x(0) + h * i For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(3) Next

K(4) = h * СИСТЕМ(Массив)

z(j, i) = z(j, i — 1) + (K(1) + 2 * K(2) + 2 * K(3) + K(4)) / 6

For i = 1 To m c(i) = z(i, n) Next

РУНГЕ = c End Function Sub InstallFunc3()

Application.MacroOptions Macro:=»РУНГЕ», Description:= _ «Возвращает значения yi, полученн^1е методом Рунге-Кутта» End Sub

В листинге 2 массивы аналогичные массивам листинга 1, только:

K(1 To 4) — массив значений, вычисляемых по формулам (2.2).

Решение примера 1.1 с помощью функции РУНГЕ показано на рисунке 2.1.

3 0,2 0,210342 1,011061

4 0,3 0,316676 1,033103

5 0,4 0,425336 1,066488

Рис. 2.1 — Вид решения примера 1.1 функцией РУНГЕ Решение примера 1.2 с помощью функции РУНГЕ показано на рисунке 2.2.

Л I=РУН ГЕ(0; А2; [1; 2; 3 А2/0,1)>

2 0,1 1,5535 2,4423 3,3321

3 0,2 2,192731 2,933636 3,77449

4 0,3 2,940906 3,644213 4,34752

5 0,4 3,325591 4,451042 5,076493

6 0,5 4,330289 5,436502 5,992716

Рис. 2.2 — Вид решения примера 1.2 функцией РУНГЕ Решение примера 1.3 с помощью функции РУНГЕ показано на рисунке 2.3.

Рис. 2.3 — Вид решения примера 1.3 функцией РУНГЕ

Пример 2.1. Построить с помощью функции РУНГЕ графики численности популяций, описываемых системой Вольтерра — Лотка

при начальных условиях Х1(0)=3, х2(0)=1; параметр 1 принимает значения от 0 до 3.

Расчетная таблица строится по аналогии с таблицей примера 1.1, значения независимой переменной в диапазоне А1:А31, в ячейку В2 вводится формула =РУНГЕ(0;А2;;А2/0,01). По таблице строятся графики численности популяций (рис. 2.4).

4 3,5 3 2,5 2 1,5 1

0 0,5 1 1,5 2 2,5 3 Рис. 2.4 — Графики численности популяций

1. Программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка, публикуются впервые.

2. Как показывают примеры, применение рассматриваемых функций не вызывает трудностей, избавляет от больших объемов рутинных вычислений, позволяет получать результаты по такому сложному разделу, как численные методы решения систем дифференциальных уравнений, на современном (цифровом) уровне.

3. Рассматриваемые пользовательские функции будут полезны как в научных исследования, связанных с системами обыкновенных дифференциальных уравнений 1 -го порядка, так и в учебном процессе.

Конфликт интересов Conflict of Interest

Не указан. None declared.

Список литературы / References

1. Бахвалов Н.С. Численные методы. / Н. С. Бахвалов — М: Наука, 1975. — 632 с.

2. Березин И.С. Методы вычислений, т. II. / И. С. Березин, Н. П. Жидков — М.: ГИФМЛ, 1959. — 620 с.

3. Гарнаев А.Ю. MS Excel 2002: разработка приложений. / А. Ю. Гарнаев — СПб.: БХВ-Петербург, 2003. — 768 с.

4. Кузьменко В.Г. VBA 2003. / В. Г. Кузьменко — М: ООО «Бином-Пресс», 2004, 432 с.

5. Ларсен Р.У. Инженерные расчеты в Excel: Пер. с англ. / Р. У. Ларсен — М.: Издательский дом «Вильямс», 2002. -544 с.

6. Самарский А.А. Задачи и упражнения по численным методам: Учебное пособие. / А. А. Самарский, П. Н. Вабищевич, Е. А. Самарская — М.: Эдиториал УРСС, 2000. — 208 с.

7. Сдвижков О.А. Excel — VBA. Словарь-справочник пользователя / О. А. Сдвижков. — М.: Эксмо, 2008. — 224 с.

8. Сдвижков О.А. Пользовательские функции VBA Excel для численного решения задачи Коши ОДУ 1-го порядка / Сдвижков О.А. // Международный научно-исследовательский журнал, № 4 (106), 2021, Часть 1, стр. 35 — 40.

9. Эрроусмит Д. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями: Пер. с англ. / Д. Эрроусмит, К. Плейс. — М.: Мир, 1986. — 243 с.

10. Сдвижков О.А. DEcode (пользовательские функции) [Электронный ресурс]. — URL: https://oas.ucoz.com/load/odu_polzovatelskie_funkcii/1-1-0-35 (дата обращения: 20.01.2021)

Список литературы на английском языке / References in English

1. Bakhvalov N. S. Chislennye metody [Numerical Methods] / N. S. Bakhvalov-M: Nauka, 1975 — 632 p. [in Russian]

2. Berezin I. S. Metody vychislenijj, t. II. [Methods of Calculations, vol. 2] / I. S. Berezin, N. P. Zhidkov-M.: GIFML, 1959 — 620 p. [in Russian]

3. Garnaev A. Yu. MS Excel 2002: razrabotka prilozhenijj [MS Excel 2002: Application Development] / A. Yu. Garnaev -St. Petersburg: BKhV-Petersburg, 2003 — 768 p. [in Russian]

4. Kuzmenko V. G. VBA 2003 / V. G. Kuzmenko-M: «Binom-Press» LLC, 2004, 432 p. [in Russian]

5. Larsen R. U. Inzhenernye raschety v Excel: Per. s angl. [Engineering Calculations in Excel: Translation from English] / R. U. Larsen-M.: Publishing house «Vilyams», 2002 — 544 p. [in Russian]

6. Samarsky A. A. Zadachi i uprazhnenija po chislennym metodam: Uchebnoe posobie [Problems and Exercises in Numerical Methods: A Textbook] / A. Samara, P. N. Vabishchevich, E. A. Samarskaya -M.: Ehditorial URSS, 2000 — 208 p. [in Russian]

7. Sdvizhkov O. A. Excel — VBA. Slovar’-spravochnik pol’zovatelja [Excel — VBA. Dictionary-User reference] / O. A. Sdvizhkov. — M.: Eksmo, 2008 — 224 p. [in Russian]

8. Sdvizhkov O. A. Pol’zovatel’skie funkcii VBA Excel dlja chislennogo reshenija zadachi Koshi ODU 1-go porjadka [Custom Excel VBA Functions For Numerical Solution of a First-Order Cauchy Ode] / O. A. Sdvizhkov // Mezhdunarodnyjj nauchno-issledovatel’skijj zhurnal [International Research Journal], No. 4 (106), 2021, Part 1, pp. 35-40 [in Russian]

9. Arrowsmith D. Obyknovennye differencial’nye uravnenija. Kachestvennaja teorija s prilozhenijami [Ordinary Differential Equations: A Qualitative Approach with Applications]: Translation from English / D. Arrowsmith, C. M. Place. — Moscow: Mir, 1986 — 243 p. [in Russian]

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

f(x)

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

«равно»

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

«равно»

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.