Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
- Предупреждение
- Симплекс метод
- Примеры решения ЗЛП симплекс методом
- Примеры решения ЗЛП методом искусственного базиса
- Калькулятор симплекс-метода
- Как пользоваться калькулятором
- Что умеет калькулятор симплекс-метода
- Что такое симплекс-метод
- Алгоритм решения основной задачи ЛП симплекс-методом
- Формирование начального базиса
- Избавляемся от отрицательных свободных коэффициентов
- Онлайн Калькулятор: Симплекс Метод
- Пример решения
- 📸 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Урок 3. Решение задачи симплекс-методом. Для тех, кто не разобрался с алгоритмом симплекс-метода.Скачать

Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Видео:Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать

Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
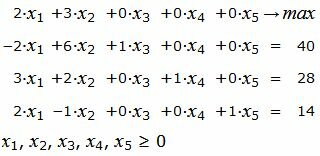 |
Р е ш е н и е. Матрица коэффициентов 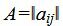
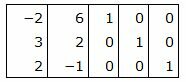 |
Правая часть ограничений системы уравнений имеет вид:
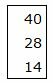 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные 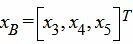
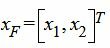
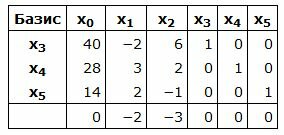 |
Запишем текущий опорный план:
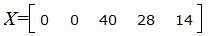 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем 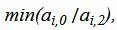
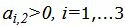
Симплекс таблица примет следующий вид:
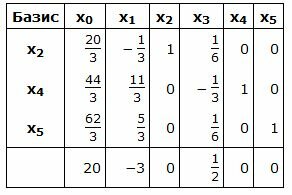 |
Запишем текущий опорный план:
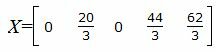 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем 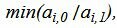
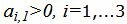
Симплекс таблица примет следующий вид:
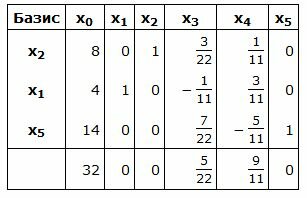 |
Запишем текущий опорный план:
 |
Текущий опорный план является оптимальным, так как в строках 4 под переменными 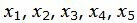
Решение можно записать так: 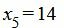
Значение целевой функции в данной точке: F(X)=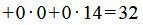
Пример 2. Найти максимум функции
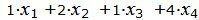 |
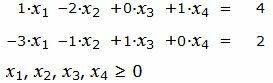 |
Р е ш е н и е. Матрица коэффициентов 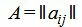
 |
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1:
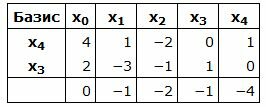 |
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
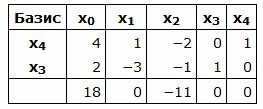 |
Запишем текущий опорный план:
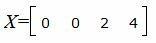 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем 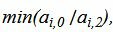
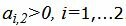
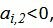
Видео:СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСкачать

Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
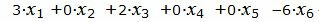 |
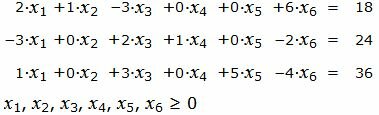 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
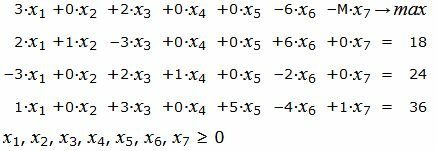 |
Матрица коэффициентов 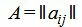
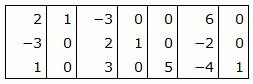 |
Правая часть ограничений системы уравнений имеет вид:
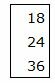 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
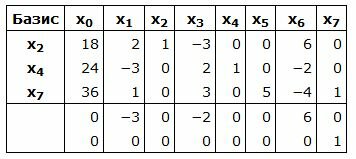 |
Базисные векторы 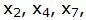
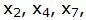
Обнулим все элементы столбца 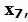
Симплекс таблица примет вид:
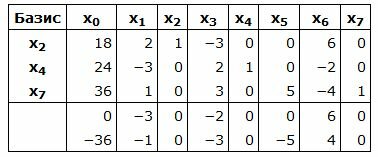 |
Запишем текущий опорный план:
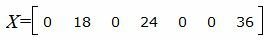 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор 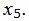
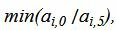
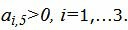
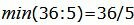
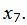
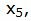
Симплекс таблица примет следующий вид:
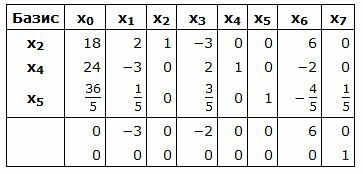 |
Запишем текущий опорный план:
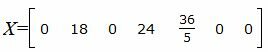 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор 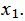

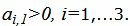
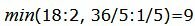
Симплекс таблица примет следующий вид:
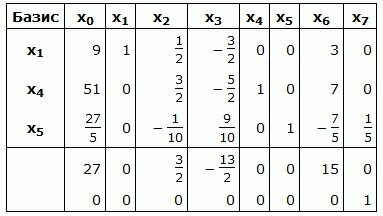 |
Запишем текущий опорный план:
 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем 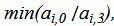
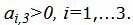
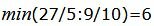
Симплекс таблица примет следующий вид:
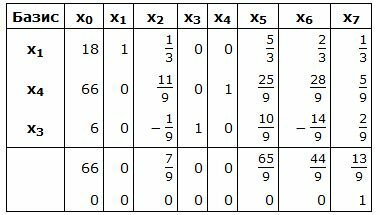 |
Запишем текущий опорный план:
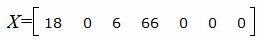 |
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными 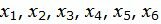
Решение исходной задачи можно записать так:
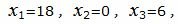 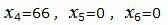 . . |
Значение целевой функции в данной точке:
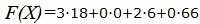 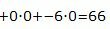 . . |
Пример 2. Найти оптимальный план задачи линейного программирования:
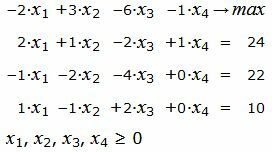 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
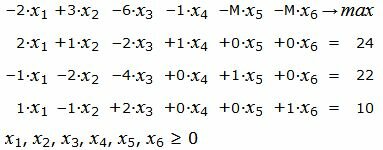 |
Матрица коэффициентов 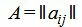
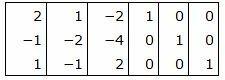 |
Правая часть ограничений системы уравнений имеет вид:
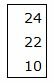 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
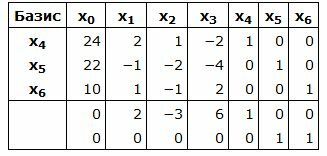 |
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
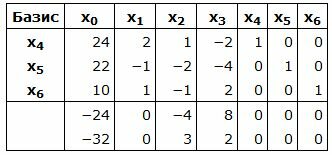 |
Запишем текущий опорный план:
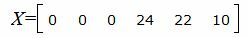 |
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Калькулятор симплекс-метода
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку «Решить»
Видео:Решение системы уравнений методом ГауссаСкачать

Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Видео:Симплекс-метод. Простое объяснение.Скачать

Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + . + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + . + an·xn v b , где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 . xn.
Видео:Cимплекс метод. Подробный разбор задачиСкачать

Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5 , предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 | -2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 | 1 | 0 | 0 | 40 | |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | . | cn | 0 | 0 | . | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | . | xn | xn+1 | xn+2 | . | xn+k | b |
| xe1 | a11 | a12 | . | a1n | a1n+1 | a1n+2 | . | a1n+k | b1 |
| xe2 | a21 | a22 | . | a2n | a2n+1 | a2n+2 | . | a2n+k | b2 |
| . | . | . | . | . | . | . | . | . | . |
| xem | am1 | am2 | . | amn | amn+1 | amn+2 | . | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
— 4·x1 — 3·x2 — 2·x3 + x4 = -33
— 3·x1 — 2·x2 — x3 + x5 = -23
— x1 — x2 — 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Видео:решение общей задачи линейного программирования Симплекс методомСкачать
Онлайн Калькулятор: Симплекс Метод
English
Русский



Решай задачи линейного программирования в режиме offline — без доступа к интернету!
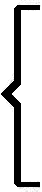 | Видео:Математика это не ИсламСкачать  Пример решения
Далее необходимо избавиться от неравенств, для чего в левую часть неравенств вводим компенсирующие переменные. Если неравенство вида ≤, то компенсирующая переменная имеет знак +, если неравенство вида ≥, то компенсирующая переменная имеет знак -. Компенсирующие переменные входят в целевую функцию задачи с нулевым коэффициентом. Теперь в системе ограничений необходимо найти достаточное количество базисных переменных. В каждом ограничении должна быть одна базисная переменная. Базисной является переменная, которая имеет при себе коэффициент 1 и встречается только в одном ограничении. Если в каком-то ограничении нет базисных переменных, то добавляем их искусственно, причем искусственные переменные входят в целевую функцию с коэффициентом -M, если целевая функция стремится к мах и с М, если целевая функция стремится к min.
Переносим в таблицу базовые элементы, которые мы определили на предварительном этапе: Элементы колонки Cb Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке. Значения упрявляемых переменных и колонки P На данном этапе никаких вычислений не нужно, просто переносим значения из предварительного этапа в соответствующие ячейки таблицы: Значение целевой функции Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений. Оценки управляемых переменных Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной. Max x 1 = ((Cb 1 * x 1,1) + (Cb 2 * x 2,1) + (Cb 3 * x 3,1) + (Cb 4 * x 4,1) + (Cb 5 * x 5,1) ) — k x 1 = ((0 * 2) + (0 * 0) + (0 * 5) + (-M * 0) + (-M * 0) ) — 3 = -3; Max x 2 = ((Cb 1 * x 1,2) + (Cb 2 * x 2,2) + (Cb 3 * x 3,2) + (Cb 4 * x 4,2) + (Cb 5 * x 5,2) ) — k x 2 = ((0 * 1) + (0 * 0) + (0 * 4) + (-M * 2) + (-M * 0) ) — 4 = -2M-4; Max x 3 = ((Cb 1 * x 1,3) + (Cb 2 * x 2,3) + (Cb 3 * x 3,3) + (Cb 4 * x 4,3) + (Cb 5 * x 5,3) ) — k x 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0; Max x 4 = ((Cb 1 * x 1,4) + (Cb 2 * x 2,4) + (Cb 3 * x 3,4) + (Cb 4 * x 4,4) + (Cb 5 * x 5,4) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0; Max x 5 = ((Cb 1 * x 1,5) + (Cb 2 * x 2,5) + (Cb 3 * x 3,5) + (Cb 4 * x 4,5) + (Cb 5 * x 5,5) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-M * 0) ) — 0 = 0; Max x 6 = ((Cb 1 * x 1,6) + (Cb 2 * x 2,6) + (Cb 3 * x 3,6) + (Cb 4 * x 4,6) + (Cb 5 * x 5,6) ) — k x 6 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * -1) + (-M * 0) ) — 0 = M; Max x 7 = ((Cb 1 * x 1,7) + (Cb 2 * x 2,7) + (Cb 3 * x 3,7) + (Cb 4 * x 4,7) + (Cb 5 * x 5,7) ) — k x 7 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * -1) ) — 0 = M; Max x 8 = ((Cb 1 * x 1,8) + (Cb 2 * x 2,8) + (Cb 3 * x 3,8) + (Cb 4 * x 4,8) + (Cb 5 * x 5,8) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 1) + (-M * 0) ) — -M = 0; Max x 9 = ((Cb 1 * x 1,9) + (Cb 2 * x 2,9) + (Cb 3 * x 3,9) + (Cb 4 * x 4,9) + (Cb 5 * x 5,9) ) — k x 9 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 1) ) — -M = 0; Элементы колонки Q Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой. Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q. Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис: Q 1 = P 1 / x 1,2 = 600 / 1 = 600; Q 2 = P 2 / x 2,2 = 225 / 0 = ∞; Q 3 = P 3 / x 3,2 = 1000 / 4 = 250; Q 4 = P 4 / x 4,2 = 150 / 2 = 75; Выводим из базиса переменную с наименьшим положительным значением Q. На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент. Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
За результатами вычислений предыдущей итерации убираем с базиса переменную x 8 и ставим на ее место x 2. Все остальные ячейки остаются без изменений. Элементы колонки Cb Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке. Значения упрявляемых переменных и колонки P (В качестве исходных данных берутся данные из предыдущей итерации) Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис: (Разрешающий элемент остается без изменений) Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент: P 4 = P 4 / x 4,2 = 150 / 2 = 75; x 4,1 = x 4,1 / x 4,2 = 0 / 2 = 0; x 4,2 = x 4,2 / x 4,2 = 2 / 2 = 1; x 4,3 = x 4,3 / x 4,2 = 0 / 2 = 0; x 4,4 = x 4,4 / x 4,2 = 0 / 2 = 0; x 4,5 = x 4,5 / x 4,2 = 0 / 2 = 0; x 4,6 = x 4,6 / x 4,2 = -1 / 2 = -0.5; x 4,7 = x 4,7 / x 4,2 = 0 / 2 = 0; x 4,8 = x 4,8 / x 4,2 = 1 / 2 = 0.5; x 4,9 = x 4,9 / x 4,2 = 0 / 2 = 0; Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента: P 1 = (P 1 * x 4,2) — (x 1,2 * P 4) / x 4,2 = ((600 * 2) — (1 * 150)) / 2 = 525; P 2 = (P 2 * x 4,2) — (x 2,2 * P 4) / x 4,2 = ((225 * 2) — (0 * 150)) / 2 = 225; P 3 = (P 3 * x 4,2) — (x 3,2 * P 4) / x 4,2 = ((1000 * 2) — (4 * 150)) / 2 = 700; P 5 = (P 5 * x 4,2) — (x 5,2 * P 4) / x 4,2 = ((0 * 2) — (0 * 150)) / 2 = 0; x 1,1 = ((x 1,1 * x 4,2) — (x 1,2 * x 4,1)) / x 4,2 = ((2 * 2) — (1 * 0)) / 2 = 2; x 1,2 = ((x 1,2 * x 4,2) — (x 1,2 * x 4,2)) / x 4,2 = ((1 * 2) — (1 * 2)) / 2 = 0; x 1,4 = ((x 1,4 * x 4,2) — (x 1,2 * x 4,4)) / x 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0; x 1,5 = ((x 1,5 * x 4,2) — (x 1,2 * x 4,5)) / x 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0; x 1,6 = ((x 1,6 * x 4,2) — (x 1,2 * x 4,6)) / x 4,2 = ((0 * 2) — (1 * -1)) / 2 = 0.5; x 1,7 = ((x 1,7 * x 4,2) — (x 1,2 * x 4,7)) / x 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0; x 1,8 = ((x 1,8 * x 4,2) — (x 1,2 * x 4,8)) / x 4,2 = ((0 * 2) — (1 * 1)) / 2 = -0.5; x 1,9 = ((x 1,9 * x 4,2) — (x 1,2 * x 4,9)) / x 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0; x 2,1 = ((x 2,1 * x 4,2) — (x 2,2 * x 4,1)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 2,2 = ((x 2,2 * x 4,2) — (x 2,2 * x 4,2)) / x 4,2 = ((0 * 2) — (0 * 2)) / 2 = 0; x 2,4 = ((x 2,4 * x 4,2) — (x 2,2 * x 4,4)) / x 4,2 = ((1 * 2) — (0 * 0)) / 2 = 1; x 2,5 = ((x 2,5 * x 4,2) — (x 2,2 * x 4,5)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 2,6 = ((x 2,6 * x 4,2) — (x 2,2 * x 4,6)) / x 4,2 = ((0 * 2) — (0 * -1)) / 2 = 0; x 2,7 = ((x 2,7 * x 4,2) — (x 2,2 * x 4,7)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 2,8 = ((x 2,8 * x 4,2) — (x 2,2 * x 4,8)) / x 4,2 = ((0 * 2) — (0 * 1)) / 2 = 0; x 2,9 = ((x 2,9 * x 4,2) — (x 2,2 * x 4,9)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 3,1 = ((x 3,1 * x 4,2) — (x 3,2 * x 4,1)) / x 4,2 = ((5 * 2) — (4 * 0)) / 2 = 5; x 3,2 = ((x 3,2 * x 4,2) — (x 3,2 * x 4,2)) / x 4,2 = ((4 * 2) — (4 * 2)) / 2 = 0; x 3,4 = ((x 3,4 * x 4,2) — (x 3,2 * x 4,4)) / x 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0; x 3,5 = ((x 3,5 * x 4,2) — (x 3,2 * x 4,5)) / x 4,2 = ((1 * 2) — (4 * 0)) / 2 = 1; x 3,6 = ((x 3,6 * x 4,2) — (x 3,2 * x 4,6)) / x 4,2 = ((0 * 2) — (4 * -1)) / 2 = 2; x 3,7 = ((x 3,7 * x 4,2) — (x 3,2 * x 4,7)) / x 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0; x 3,8 = ((x 3,8 * x 4,2) — (x 3,2 * x 4,8)) / x 4,2 = ((0 * 2) — (4 * 1)) / 2 = -2; x 3,9 = ((x 3,9 * x 4,2) — (x 3,2 * x 4,9)) / x 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0; x 5,1 = ((x 5,1 * x 4,2) — (x 5,2 * x 4,1)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 5,2 = ((x 5,2 * x 4,2) — (x 5,2 * x 4,2)) / x 4,2 = ((0 * 2) — (0 * 2)) / 2 = 0; x 5,4 = ((x 5,4 * x 4,2) — (x 5,2 * x 4,4)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 5,5 = ((x 5,5 * x 4,2) — (x 5,2 * x 4,5)) / x 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0; x 5,6 = ((x 5,6 * x 4,2) — (x 5,2 * x 4,6)) / x 4,2 = ((0 * 2) — (0 * -1)) / 2 = 0; x 5,7 = ((x 5,7 * x 4,2) — (x 5,2 * x 4,7)) / x 4,2 = ((-1 * 2) — (0 * 0)) / 2 = -1; x 5,8 = ((x 5,8 * x 4,2) — (x 5,2 * x 4,8)) / x 4,2 = ((0 * 2) — (0 * 1)) / 2 = 0; x 5,9 = ((x 5,9 * x 4,2) — (x 5,2 * x 4,9)) / x 4,2 = ((1 * 2) — (0 * 0)) / 2 = 1; Значение целевой функции Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений. Оценки управляемых переменных Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной. Max x 1 = ((Cb 1 * x 1,1) + (Cb 2 * x 2,1) + (Cb 3 * x 3,1) + (Cb 4 * x 4,1) + (Cb 5 * x 5,1) ) — k x 1 = ((0 * 2) + (0 * 0) + (0 * 5) + (4 * 0) + (-M * 0) ) — 3 = -3; Max x 2 = ((Cb 1 * x 1,2) + (Cb 2 * x 2,2) + (Cb 3 * x 3,2) + (Cb 4 * x 4,2) + (Cb 5 * x 5,2) ) — k x 2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0; Max x 3 = ((Cb 1 * x 1,3) + (Cb 2 * x 2,3) + (Cb 3 * x 3,3) + (Cb 4 * x 4,3) + (Cb 5 * x 5,3) ) — k x 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 4 = ((Cb 1 * x 1,4) + (Cb 2 * x 2,4) + (Cb 3 * x 3,4) + (Cb 4 * x 4,4) + (Cb 5 * x 5,4) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 5 = ((Cb 1 * x 1,5) + (Cb 2 * x 2,5) + (Cb 3 * x 3,5) + (Cb 4 * x 4,5) + (Cb 5 * x 5,5) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 6 = ((Cb 1 * x 1,6) + (Cb 2 * x 2,6) + (Cb 3 * x 3,6) + (Cb 4 * x 4,6) + (Cb 5 * x 5,6) ) — k x 6 = ((0 * 0.5) + (0 * 0) + (0 * 2) + (4 * -0.5) + (-M * 0) ) — 0 = -2; Max x 7 = ((Cb 1 * x 1,7) + (Cb 2 * x 2,7) + (Cb 3 * x 3,7) + (Cb 4 * x 4,7) + (Cb 5 * x 5,7) ) — k x 7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M; Max x 8 = ((Cb 1 * x 1,8) + (Cb 2 * x 2,8) + (Cb 3 * x 3,8) + (Cb 4 * x 4,8) + (Cb 5 * x 5,8) ) — k x 8 = ((0 * -0.5) + (0 * 0) + (0 * -2) + (4 * 0.5) + (-M * 0) ) — -M = M+2; Max x 9 = ((Cb 1 * x 1,9) + (Cb 2 * x 2,9) + (Cb 3 * x 3,9) + (Cb 4 * x 4,9) + (Cb 5 * x 5,9) ) — k x 9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0; Элементы колонки Q Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой. Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q. Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис: Q 1 = P 1 / x 1,1 = 525 / 2 = 262.5; Q 2 = P 2 / x 2,1 = 225 / 0 = ∞; Q 3 = P 3 / x 3,1 = 700 / 5 = 140; Выводим из базиса переменную с наименьшим положительным значением Q. На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент. Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
За результатами вычислений предыдущей итерации убираем с базиса переменную x 5 и ставим на ее место x 1. Все остальные ячейки остаются без изменений. Элементы колонки Cb Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке. Значения упрявляемых переменных и колонки P (В качестве исходных данных берутся данные из предыдущей итерации) Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис: (Разрешающий элемент остается без изменений) Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент: P 3 = P 3 / x 3,1 = 700 / 5 = 140; x 3,1 = x 3,1 / x 3,1 = 5 / 5 = 1; x 3,2 = x 3,2 / x 3,1 = 0 / 5 = 0; x 3,3 = x 3,3 / x 3,1 = 0 / 5 = 0; x 3,4 = x 3,4 / x 3,1 = 0 / 5 = 0; x 3,5 = x 3,5 / x 3,1 = 1 / 5 = 0.2; x 3,6 = x 3,6 / x 3,1 = 2 / 5 = 0.4; x 3,7 = x 3,7 / x 3,1 = 0 / 5 = 0; x 3,8 = x 3,8 / x 3,1 = -2 / 5 = -0.4; x 3,9 = x 3,9 / x 3,1 = 0 / 5 = 0; Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента: P 1 = (P 1 * x 3,1) — (x 1,1 * P 3) / x 3,1 = ((525 * 5) — (2 * 700)) / 5 = 245; P 2 = (P 2 * x 3,1) — (x 2,1 * P 3) / x 3,1 = ((225 * 5) — (0 * 700)) / 5 = 225; P 4 = (P 4 * x 3,1) — (x 4,1 * P 3) / x 3,1 = ((75 * 5) — (0 * 700)) / 5 = 75; P 5 = (P 5 * x 3,1) — (x 5,1 * P 3) / x 3,1 = ((0 * 5) — (0 * 700)) / 5 = 0; x 1,1 = ((x 1,1 * x 3,1) — (x 1,1 * x 3,1)) / x 3,1 = ((2 * 5) — (2 * 5)) / 5 = 0; x 1,3 = ((x 1,3 * x 3,1) — (x 1,1 * x 3,3)) / x 3,1 = ((1 * 5) — (2 * 0)) / 5 = 1; x 1,4 = ((x 1,4 * x 3,1) — (x 1,1 * x 3,4)) / x 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0; x 1,5 = ((x 1,5 * x 3,1) — (x 1,1 * x 3,5)) / x 3,1 = ((0 * 5) — (2 * 1)) / 5 = -0.4; x 1,6 = ((x 1,6 * x 3,1) — (x 1,1 * x 3,6)) / x 3,1 = ((0.5 * 5) — (2 * 2)) / 5 = -0.3; x 1,7 = ((x 1,7 * x 3,1) — (x 1,1 * x 3,7)) / x 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0; x 1,8 = ((x 1,8 * x 3,1) — (x 1,1 * x 3,8)) / x 3,1 = ((-0.5 * 5) — (2 * -2)) / 5 = 0.3; x 1,9 = ((x 1,9 * x 3,1) — (x 1,1 * x 3,9)) / x 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0; x 2,1 = ((x 2,1 * x 3,1) — (x 2,1 * x 3,1)) / x 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0; x 2,3 = ((x 2,3 * x 3,1) — (x 2,1 * x 3,3)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 2,4 = ((x 2,4 * x 3,1) — (x 2,1 * x 3,4)) / x 3,1 = ((1 * 5) — (0 * 0)) / 5 = 1; x 2,5 = ((x 2,5 * x 3,1) — (x 2,1 * x 3,5)) / x 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0; x 2,6 = ((x 2,6 * x 3,1) — (x 2,1 * x 3,6)) / x 3,1 = ((0 * 5) — (0 * 2)) / 5 = 0; x 2,7 = ((x 2,7 * x 3,1) — (x 2,1 * x 3,7)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 2,8 = ((x 2,8 * x 3,1) — (x 2,1 * x 3,8)) / x 3,1 = ((0 * 5) — (0 * -2)) / 5 = 0; x 2,9 = ((x 2,9 * x 3,1) — (x 2,1 * x 3,9)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 4,1 = ((x 4,1 * x 3,1) — (x 4,1 * x 3,1)) / x 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0; x 4,3 = ((x 4,3 * x 3,1) — (x 4,1 * x 3,3)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 4,4 = ((x 4,4 * x 3,1) — (x 4,1 * x 3,4)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 4,5 = ((x 4,5 * x 3,1) — (x 4,1 * x 3,5)) / x 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0; x 4,6 = ((x 4,6 * x 3,1) — (x 4,1 * x 3,6)) / x 3,1 = ((-0.5 * 5) — (0 * 2)) / 5 = -0.5; x 4,7 = ((x 4,7 * x 3,1) — (x 4,1 * x 3,7)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 4,8 = ((x 4,8 * x 3,1) — (x 4,1 * x 3,8)) / x 3,1 = ((0.5 * 5) — (0 * -2)) / 5 = 0.5; x 4,9 = ((x 4,9 * x 3,1) — (x 4,1 * x 3,9)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 5,1 = ((x 5,1 * x 3,1) — (x 5,1 * x 3,1)) / x 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0; x 5,3 = ((x 5,3 * x 3,1) — (x 5,1 * x 3,3)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 5,4 = ((x 5,4 * x 3,1) — (x 5,1 * x 3,4)) / x 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0; x 5,5 = ((x 5,5 * x 3,1) — (x 5,1 * x 3,5)) / x 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0; x 5,6 = ((x 5,6 * x 3,1) — (x 5,1 * x 3,6)) / x 3,1 = ((0 * 5) — (0 * 2)) / 5 = 0; x 5,7 = ((x 5,7 * x 3,1) — (x 5,1 * x 3,7)) / x 3,1 = ((-1 * 5) — (0 * 0)) / 5 = -1; x 5,8 = ((x 5,8 * x 3,1) — (x 5,1 * x 3,8)) / x 3,1 = ((0 * 5) — (0 * -2)) / 5 = 0; x 5,9 = ((x 5,9 * x 3,1) — (x 5,1 * x 3,9)) / x 3,1 = ((1 * 5) — (0 * 0)) / 5 = 1; Значение целевой функции Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений. Оценки управляемых переменных Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной. Max x 1 = ((Cb 1 * x 1,1) + (Cb 2 * x 2,1) + (Cb 3 * x 3,1) + (Cb 4 * x 4,1) + (Cb 5 * x 5,1) ) — k x 1 = ((0 * 0) + (0 * 0) + (3 * 1) + (4 * 0) + (-M * 0) ) — 3 = 0; Max x 2 = ((Cb 1 * x 1,2) + (Cb 2 * x 2,2) + (Cb 3 * x 3,2) + (Cb 4 * x 4,2) + (Cb 5 * x 5,2) ) — k x 2 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0; Max x 3 = ((Cb 1 * x 1,3) + (Cb 2 * x 2,3) + (Cb 3 * x 3,3) + (Cb 4 * x 4,3) + (Cb 5 * x 5,3) ) — k x 3 = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 4 = ((Cb 1 * x 1,4) + (Cb 2 * x 2,4) + (Cb 3 * x 3,4) + (Cb 4 * x 4,4) + (Cb 5 * x 5,4) ) — k x 4 = ((0 * 0) + (0 * 1) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 5 = ((Cb 1 * x 1,5) + (Cb 2 * x 2,5) + (Cb 3 * x 3,5) + (Cb 4 * x 4,5) + (Cb 5 * x 5,5) ) — k x 5 = ((0 * -0.4) + (0 * 0) + (3 * 0.2) + (4 * 0) + (-M * 0) ) — 0 = 0.6; Max x 6 = ((Cb 1 * x 1,6) + (Cb 2 * x 2,6) + (Cb 3 * x 3,6) + (Cb 4 * x 4,6) + (Cb 5 * x 5,6) ) — k x 6 = ((0 * -0.3) + (0 * 0) + (3 * 0.4) + (4 * -0.5) + (-M * 0) ) — 0 = -0.8; Max x 7 = ((Cb 1 * x 1,7) + (Cb 2 * x 2,7) + (Cb 3 * x 3,7) + (Cb 4 * x 4,7) + (Cb 5 * x 5,7) ) — k x 7 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * -1) ) — 0 = M; Max x 8 = ((Cb 1 * x 1,8) + (Cb 2 * x 2,8) + (Cb 3 * x 3,8) + (Cb 4 * x 4,8) + (Cb 5 * x 5,8) ) — k x 8 = ((0 * 0.3) + (0 * 0) + (3 * -0.4) + (4 * 0.5) + (-M * 0) ) — -M = M+0.8; Max x 9 = ((Cb 1 * x 1,9) + (Cb 2 * x 2,9) + (Cb 3 * x 3,9) + (Cb 4 * x 4,9) + (Cb 5 * x 5,9) ) — k x 9 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 1) ) — -M = 0; Элементы колонки Q Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой. Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q. Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис: Q 1 = P 1 / x 1,6 = 245 / -0.3 = -816.67; Q 2 = P 2 / x 2,6 = 225 / 0 = ∞; Q 3 = P 3 / x 3,6 = 140 / 0.4 = 350; Q 4 = P 4 / x 4,6 = 75 / -0.5 = -150; Выводим из базиса переменную с наименьшим положительным значением Q. На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент. Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
За результатами вычислений предыдущей итерации убираем с базиса переменную x 1 и ставим на ее место x 6. Все остальные ячейки остаются без изменений. Элементы колонки Cb Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке. Значения упрявляемых переменных и колонки P (В качестве исходных данных берутся данные из предыдущей итерации) Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис: (Разрешающий элемент остается без изменений) Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент: P 3 = P 3 / x 3,6 = 140 / 0.4 = 350; x 3,1 = x 3,1 / x 3,6 = 1 / 0.4 = 2.5; x 3,2 = x 3,2 / x 3,6 = 0 / 0.4 = 0; x 3,3 = x 3,3 / x 3,6 = 0 / 0.4 = 0; x 3,4 = x 3,4 / x 3,6 = 0 / 0.4 = 0; x 3,5 = x 3,5 / x 3,6 = 0.2 / 0.4 = 0.5; x 3,6 = x 3,6 / x 3,6 = 0.4 / 0.4 = 1; x 3,7 = x 3,7 / x 3,6 = 0 / 0.4 = 0; x 3,8 = x 3,8 / x 3,6 = -0.4 / 0.4 = -1; x 3,9 = x 3,9 / x 3,6 = 0 / 0.4 = 0; Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента: P 1 = (P 1 * x 3,6) — (x 1,6 * P 3) / x 3,6 = ((245 * 0.4) — (-0.3 * 140)) / 0.4 = 350; P 2 = (P 2 * x 3,6) — (x 2,6 * P 3) / x 3,6 = ((225 * 0.4) — (0 * 140)) / 0.4 = 225; P 4 = (P 4 * x 3,6) — (x 4,6 * P 3) / x 3,6 = ((75 * 0.4) — (-0.5 * 140)) / 0.4 = 250; P 5 = (P 5 * x 3,6) — (x 5,6 * P 3) / x 3,6 = ((0 * 0.4) — (0 * 140)) / 0.4 = 0; x 1,1 = ((x 1,1 * x 3,6) — (x 1,6 * x 3,1)) / x 3,6 = ((0 * 0.4) — (-0.3 * 1)) / 0.4 = 0.75; x 1,2 = ((x 1,2 * x 3,6) — (x 1,6 * x 3,2)) / x 3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0; x 1,3 = ((x 1,3 * x 3,6) — (x 1,6 * x 3,3)) / x 3,6 = ((1 * 0.4) — (-0.3 * 0)) / 0.4 = 1; x 1,4 = ((x 1,4 * x 3,6) — (x 1,6 * x 3,4)) / x 3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0; x 1,5 = ((x 1,5 * x 3,6) — (x 1,6 * x 3,5)) / x 3,6 = ((-0.4 * 0.4) — (-0.3 * 0.2)) / 0.4 = -0.25; x 1,6 = ((x 1,6 * x 3,6) — (x 1,6 * x 3,6)) / x 3,6 = ((-0.3 * 0.4) — (-0.3 * 0.4)) / 0.4 = 0; x 1,8 = ((x 1,8 * x 3,6) — (x 1,6 * x 3,8)) / x 3,6 = ((0.3 * 0.4) — (-0.3 * -0.4)) / 0.4 = 0; x 1,9 = ((x 1,9 * x 3,6) — (x 1,6 * x 3,9)) / x 3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0; x 2,1 = ((x 2,1 * x 3,6) — (x 2,6 * x 3,1)) / x 3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0; x 2,2 = ((x 2,2 * x 3,6) — (x 2,6 * x 3,2)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 2,3 = ((x 2,3 * x 3,6) — (x 2,6 * x 3,3)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 2,4 = ((x 2,4 * x 3,6) — (x 2,6 * x 3,4)) / x 3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1; x 2,5 = ((x 2,5 * x 3,6) — (x 2,6 * x 3,5)) / x 3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0; x 2,6 = ((x 2,6 * x 3,6) — (x 2,6 * x 3,6)) / x 3,6 = ((0 * 0.4) — (0 * 0.4)) / 0.4 = 0; x 2,8 = ((x 2,8 * x 3,6) — (x 2,6 * x 3,8)) / x 3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0; x 2,9 = ((x 2,9 * x 3,6) — (x 2,6 * x 3,9)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 4,1 = ((x 4,1 * x 3,6) — (x 4,6 * x 3,1)) / x 3,6 = ((0 * 0.4) — (-0.5 * 1)) / 0.4 = 1.25; x 4,2 = ((x 4,2 * x 3,6) — (x 4,6 * x 3,2)) / x 3,6 = ((1 * 0.4) — (-0.5 * 0)) / 0.4 = 1; x 4,3 = ((x 4,3 * x 3,6) — (x 4,6 * x 3,3)) / x 3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0; x 4,4 = ((x 4,4 * x 3,6) — (x 4,6 * x 3,4)) / x 3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0; x 4,5 = ((x 4,5 * x 3,6) — (x 4,6 * x 3,5)) / x 3,6 = ((0 * 0.4) — (-0.5 * 0.2)) / 0.4 = 0.25; x 4,6 = ((x 4,6 * x 3,6) — (x 4,6 * x 3,6)) / x 3,6 = ((-0.5 * 0.4) — (-0.5 * 0.4)) / 0.4 = 0; x 4,8 = ((x 4,8 * x 3,6) — (x 4,6 * x 3,8)) / x 3,6 = ((0.5 * 0.4) — (-0.5 * -0.4)) / 0.4 = 0; x 4,9 = ((x 4,9 * x 3,6) — (x 4,6 * x 3,9)) / x 3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0; x 5,1 = ((x 5,1 * x 3,6) — (x 5,6 * x 3,1)) / x 3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0; x 5,2 = ((x 5,2 * x 3,6) — (x 5,6 * x 3,2)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 5,3 = ((x 5,3 * x 3,6) — (x 5,6 * x 3,3)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 5,4 = ((x 5,4 * x 3,6) — (x 5,6 * x 3,4)) / x 3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0; x 5,5 = ((x 5,5 * x 3,6) — (x 5,6 * x 3,5)) / x 3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0; x 5,6 = ((x 5,6 * x 3,6) — (x 5,6 * x 3,6)) / x 3,6 = ((0 * 0.4) — (0 * 0.4)) / 0.4 = 0; x 5,8 = ((x 5,8 * x 3,6) — (x 5,6 * x 3,8)) / x 3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0; x 5,9 = ((x 5,9 * x 3,6) — (x 5,6 * x 3,9)) / x 3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1; Значение целевой функции Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений. Оценки управляемых переменных Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной. Max x 1 = ((Cb 1 * x 1,1) + (Cb 2 * x 2,1) + (Cb 3 * x 3,1) + (Cb 4 * x 4,1) + (Cb 5 * x 5,1) ) — k x 1 = ((0 * 0.75) + (0 * 0) + (0 * 2.5) + (4 * 1.25) + (-M * 0) ) — 3 = 2; Max x 2 = ((Cb 1 * x 1,2) + (Cb 2 * x 2,2) + (Cb 3 * x 3,2) + (Cb 4 * x 4,2) + (Cb 5 * x 5,2) ) — k x 2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0; Max x 3 = ((Cb 1 * x 1,3) + (Cb 2 * x 2,3) + (Cb 3 * x 3,3) + (Cb 4 * x 4,3) + (Cb 5 * x 5,3) ) — k x 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 4 = ((Cb 1 * x 1,4) + (Cb 2 * x 2,4) + (Cb 3 * x 3,4) + (Cb 4 * x 4,4) + (Cb 5 * x 5,4) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 5 = ((Cb 1 * x 1,5) + (Cb 2 * x 2,5) + (Cb 3 * x 3,5) + (Cb 4 * x 4,5) + (Cb 5 * x 5,5) ) — k x 5 = ((0 * -0.25) + (0 * 0) + (0 * 0.5) + (4 * 0.25) + (-M * 0) ) — 0 = 1; Max x 6 = ((Cb 1 * x 1,6) + (Cb 2 * x 2,6) + (Cb 3 * x 3,6) + (Cb 4 * x 4,6) + (Cb 5 * x 5,6) ) — k x 6 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0; Max x 7 = ((Cb 1 * x 1,7) + (Cb 2 * x 2,7) + (Cb 3 * x 3,7) + (Cb 4 * x 4,7) + (Cb 5 * x 5,7) ) — k x 7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M; Max x 8 = ((Cb 1 * x 1,8) + (Cb 2 * x 2,8) + (Cb 3 * x 3,8) + (Cb 4 * x 4,8) + (Cb 5 * x 5,8) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-M * 0) ) — -M = M; Max x 9 = ((Cb 1 * x 1,9) + (Cb 2 * x 2,9) + (Cb 3 * x 3,9) + (Cb 4 * x 4,9) + (Cb 5 * x 5,9) ) — k x 9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0; Поскольку среди оценок управляемых переменных нет отрицательных значений, текущая таблица имеет оптимальное решение. Значение целевой функции: Переменные которые присутствуют в базисе, равны соответствующим ячейкам колонки P, все остальные переменные равны нулю: 📸 ВидеоРешение задачи линейного программирования при помощи надстройки Поиск решенияСкачать  Симплексный метод (табличный оформление №1) решения задачи линейного программирования.Скачать  Простая задача линейного программирования №1. Симплекс-метод для поиска минимума.Скачать 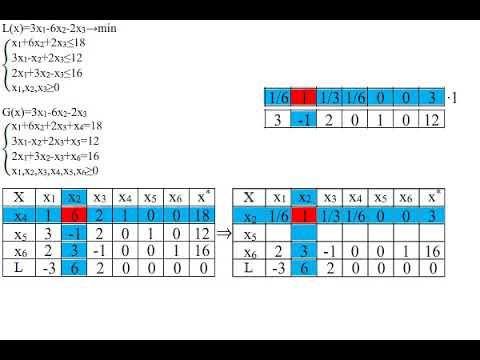 Транспортная задача (Симплекс метод)Скачать  МОР МПУР Симплекс метод решения задач линейного программирования ЗЛП ПримерСкачать  Симплекс-метод (пример)Скачать  Лекция 2 Симплекс-методСкачать  Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать  Урок 1. Решение задачи линейного программирование в Excel с помощью надстройки «Поиск решения»Скачать  Решение системы линейных уравнений методом ГауссаСкачать  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
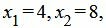
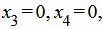

 Русский
Русский