Решение систем уравнений с разреженными матрицами (3 видео)

Решение систем уравнений с разреженными матрицами

Рассматриваются технологические проблемы реализации параллельных алгоритмов решения систем линейных алгебраических уравнений (СЛАУ) с большими разреженными матрицами общего вида, возникающими при построении Марковских моделей. Проводится классификация методов хранения разреженных матриц и методов решения СЛАУ. Описываются сложности и основные пути достижения высокой производительности программного обеспечения при использовании многопроцессорных вычислительных систем с разделяемой памятью на основе применения MPI.

Содержание

Общая постановка проблемы.
Постановка задач исследования.
Выбор метода решения СЛАУ
Схемы хранения разреженных матриц
Выводы.
Книга: Решение систем линейных алгебраических уравнений для больших разреженных матриц
Решение разреженных СЛАУ больших размерностей средствами ManagedCuda в .NET
Постановка задачи
Математическая библиотека Math.Net Numerics
Библиотека ManagedCuda
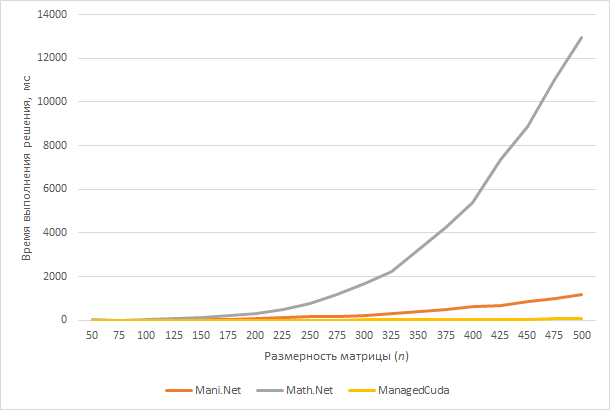
Вычислительный эксперимент: анализ временных затрат на решению СЛАУ различными технологиями
Заключение
🔍 Видео

Общая постановка проблемы.

При численном исследовании стационарных и нестационарных, линейных и нелинейных процессов в задачах математического моделирования, в том числе оптимизационных и междисциплинарных, многократное решение СЛАУ является наиболее ресурсоемким этапом. Матрицы таких задач имеют разреженную структуру и в большинстве случаев могут быть сведены путем оптимизации нумерации неизвестных к ленточным, профильным, блочным и другим.

В научной литературе широко представлены методы решения СЛАУ для матриц особого вида или сводящихся к ним [1,2].

Постановка задач исследования.

В данной работе рассматриваются разреженные матрицы общего вида, получаемые при построении Марковских моделей вычислительных систем. Порядок возникающих матриц – от десятков и сотен тысяч до десятков миллионов. Это вызвано желанием оперировать более точными дискретными моделями, позволяющими получать приближенные решения, более близкие к решениям исходных задач, лучше учитывать локальные особенности рассматриваемого процесса.

Решение таких задач требует значительных вычислительных ресурсов, которые могут быть представлены параллельными компьютерами. Поэтому является актуальной проблема создания параллельных алгоритмов решения данной задачи.

Однако до разработки подобных параллельных алгоритмов следует решить две подзадачи:
1) Выбрать эффективный метод хранения ненулевых элементов
2) Выбрать аналитический метод решения СЛАУ.

Выбор метода решения СЛАУ

Методы решения большинства задач численных методов (в том числе задач решения линейных алгебраических систем) можно разделить на два типа: прямые и итерационные.

Метод решения задачи называется прямым, если он дает ее точное решение за конечное число действий.

Метод решения задачи называется итерационным, если он дает точное решение как предел последовательности приближений , вычисляемых по единообразной схеме, то есть где x — точное решение задачи, x(k) — k-тое приближение (итерация) к решению.

При реализации итерационного метода на ЭВМ его приходится обрывать на каком-то приближении с номером K и полагать x ≈ x (k) . Обычно указывают погрешность (точность) ε, с которой требуется найти решение x и условие окончания итераций задают таким образом, чтобы норма разности точного решения и очередного итерационного приближения не превышала ||x — x(k)|| ≤ ε.

К прямым методам решения СЛАУ относятся известный из алгебры метод Крамера, метод Гаусса и его модификации и другие, к итерационным — метод простой итерации, метод Зейделя и другие.

Стандартные прямые методы, такие как поиск обратной матрицы (численно неустойчив) или метод Гаусса не учитывают разреженность матрицы А и мало подходят для программирования, особенно в нашем конкретном случае – при преобразованиях исходной матрицы А на каждом шаге возникает вычислительная погрешность, связанная с конечным числом разрядов ЭВМ для представления вещественных чисел.

Эффективность применения приближенных методов зависят от выбора начального вектора и быстроты сходимости процесса.

Рассмотрим метод простой итерации (метод последовательных приближений). Пусть дана система n линейных уравнений с n неизвестными:

Обозначим ; , где i = 1, 2, . n; j = 1,2. n. Тогда система (2) запишется таким образом в матричной форме

Решим систему (2) методом последовательных приближений. За нулевое приближение примем столбец свободных членов. Любое (k+1)-е приближение вычисляют по формуле

Если последовательность приближений x(0). x(k) имеет предел , то этот предел является решением системы (1), поскольку в силу свойства предела , т.е. [2].

Метод Зейделя [3] представляет собой модификацию метода последовательных приближений. В методе Зейделя при вычислении (k+1)-го приближения неизвестного xi (i>1) учитываются уже найденные ранее (k+1)-е приближения неизвестных xi-1.

Пусть дана линейная система, приведенная к нормальному виду:

Выбираем произвольно начальные приближения неизвестных и подставляем в первое уравнение системы (3). Полученное первое приближение подставляем во второе уравнение системы и так далее до последнего уравнения. Аналогично строим вторые, третьи и т.д. итерации.

Таким образом, предполагая, что k-е приближения известны, методом Зейделя строим (k+1)-е приближение по следующим формулам: , где k=0,1. n

Представленные методы в их классической постановке не могут использоваться при работе с разреженными матрицами, так как матрица коэффициентов хранится в одной из специальных форм, обзор которых приводится ниже.

Также следует отметить, что при выборе алгоритма должны учитываться вероятные:
— ошибки округления в операциях с плавающей запятой;
— численную устойчивость.

Схемы хранения разреженных матриц

Основной целью является хранение только ненулевых элементов матрицей и возможность производить над ней простейшие матричные операции.

Пусть Nz – количество ненулевых элементов матрицы A. Рассмотрим наиболее распространенные схемы хранения, более подробная информация приводится в [4].

Самой простой схемой хранения разреженных матриц является так называемый «координатный» формат. Структура исходной матрицы отображается на три одномерных массива: (1) – массив, содержащий значения ненулевых элементов матрицы А в произвольном порядке; (2) целочисленный массив, содержащий их строковые индексы; и (3) целочисленный массив, содержащий их столбцовые индексы. Все три вектора имеют длину Nz.

Пример 1. Матрица

Может быть представлена как:

AA	12	9	7	5	1	2	11	3	6	4	8	10
JR	5	3	3	2	1	1	4	2	3	2	3	4
JC	5	5	3	4	1	4	4	1	1	2	4	3

В приведенном примере элементы перечислены в произвольном порядке, однако обычно они перечисляются по строкам или столбцам. Если элементы перечисляются по строкам, то вектор JC, который содержит избыточную информацию, может быть заменен массивом указателей на начало каждой строки. Это даст заметную экономию при хранении. Новая структура данных будет иметь три массива, которые будут выполнять следующие функции:

— массив АА содержит ненулевые значения aij, сохраняемые построчно, от строки 1 до n. Длина массива АА есть Nz.

— целочисленный массив JA содержит столбцовые индексы элементов aij в матрице А. Длина массива JА есть Nz.

— целочисленный массив содержит указатели входа для каждой строки в массивах АА и JА. Таким образом, значение IA(i) показывается позиция, где начинается i-тая строка в массивах АА и JА. Длина IA есть n+1, где IA(n+1) содержит число IA(1)+ Nz, то есть адрес в А и JА начала фиктивной строки с номером n+1.

Таким образом, представленная выше матрица А может быть сохранена как:

AA	1	2	3	4	5	6	7	8	9	10	11	12
JА	1	4	1	2	4	1	3	4	5	3	4	5
IA	1	3	6	10	12	13

Такой формат является наиболее популярным для хранения разреженных матриц общего вида. Он носит название разреженного строчного формата или Compressed Sparse Row (CSR). Эта схема более предпочтительна, чем координатная, так как часто является более удобной для нескольких важных операций над разреженными матрицами: сложения, умножения, перестановок строк и столбцов, транспонирования, решения ли-нейных систем с разреженными матрицами коэффициентов как прямыми, так и итерационными методами. С другой стороны, координатная схема более проста, наглядна и гибка, она часто используется в качестве «входного» формата для вычислительных библиотек, предназначенных для работы с разреженными матрицами.

Существует несколько модификаций данной схемы хранения, наиболее очевидной является разреженная столбцовая схема или Compressed Sparse Column (CSC).

Другая распространенная схема учитывает тот факт, что диагональные элементы большинства матриц ненулевые и/или используются чаще других. Модифицированная строчная схема (Modified Sparse Row, MSR) использует только два массива: массив значении АА и целочисленный массив JА. В первых n позициях АА содержит диагональные элементы исходной матрицы по порядку. Элемент АА(n+1) не заполняется (или же несет дополнительную информацию о матрице). Начиная с позиции n+2 записываются ненулевые элементы исходной матрицы по строкам, исключая диагональные. Для каждого элемента АА(k) элемент JA(k) показывает столбцовый индекс в исходной матрице. На n+1 позициях матрицы JA размещаются указатели входа для каждой строки матрицы АА и JA.

Поэтому для матрицы из примера выше эти два массива будут иметь вид:

AA	1	4	7	11	12	*	2	3	5	6	8	9	10
JА	7	8	10	13	14	14	4	1	4	1	4	5	3

Звездочка указывает на неиспользуемый элемент. Заметим, что JA(n)=JA(n+1)=14, показывая, что последняя строка является нулевой, так как диагональный элемент уже описан ранее.

Диагонально структурированные матрицы – это матрицы, чьи ненулевые элементы расположены вдоль небольшого числа диагоналей. Эти диагонали могут храниться в прямоугольном массиве DIAG(1:n, 1:Nd), где Nd–число диагоналей. Смещение каждой диагонали вычисляется относительно главной диагонали, которая должна быть известна. Смещения хранятся в массиве IOFF(1:Nd). Таким образом, элемент ai,i+ioff(j) исходной матрицы будет храниться в позиции (i,j) в массиве DIAG. Порядок, в каком хранятся диагонали, в общем случае, неважен, особенно если большинство операций сосредоточенно около главной диагонали, ее имеет смысл хранить в первом столбце. Также следует отметить, что все диагонали, кроме главной, имеют менее n элементов, так что не все элементы матрицы DIAG будут использоваться.

Пример 2. Трехдиагональная матрица

может быть сохранена в двух массивах согласно вышеприведенной схеме:
DIAG =

*	1	2
3	4	5
6	7	8
9	10	*
11	12	*

IOFF =

-1

Более общей схемой, популярной для векторных машин является так называемый формат. Эта схема предполагает, что количество диагоналей Nd невелико. Для хранения требуются два прямоугольных массива размером n*Nd каждый.

В первом, COEF, подобном DIAG, хранятся ненулевые элементы матрицы А. Ненулевые элементы каждой строки могут сохраняться в строке массива COEF(1:n,1:Nd), дополняя эту строку нулями, если необходимо. Вместе с COEF, целочисленный массив JCOEF(1:n,1:Nd) должен хранить индекс столбца каждого элемента COEF.

Для матрицы А из примера 2, схема хранения Ellpack-Itpack примет вид:
COEF =

1	2	0
3	4	5
6	7	8
9	10	0
11	12	0

JCOEF =

1	3	1
1	2	4
2	3	5
3	4	4
4	5	5

Выводы.

Приписывание матрице свойства разреженности эквивалентно утверждению о существовании алгоритма, использующего ее разреженность и делающего вычисления с ней дешевле по сравнению со стандартными алгоритмами.

Ввиду трудоемкости решения СЛАУ для разреженных матриц следует направить исследования на разработку эффективных параллельных алгоритмов для разреженных матриц общего вида, получаемых при построении Марковских моделей вычислительных систем. Можно сформулировать три основных требования к алгоритмам, оперирующим разреженными матрицами: хранить только ненулевые элементы, оперировать только с ненулевыми элементами и сохранять разреженность. Многие схемы хранения допускают определенную долю нулей, и алгоритм обрабатывает их, как если бы они не были нулями. Алгоритм, хранящий и обрабатывающий меньшее число нулей, более сложен, труднее программируется и целесообразен только для достаточно больших матриц.

Видео:Матричный метод решения систем уравненийСкачать

Книга: Решение систем линейных алгебраических уравнений для больших разреженных матриц

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГO

“ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ”

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ДЛЯ БОЛЬШИХ РАЗРЕЖЕННЫХ МАТРИЦ

В.А.Еремеев. Решение систем линейных алгебраических уравнений для больших разреженных матриц: Учебно-методическое пособие. – г.Ростов-на-Дону, 2008 г. – 39 с.

В данном пособии в концентрированном виде содержится информация о решении систем линейных алгебраических уравнений для разреженных матриц большой размерности. Пособие состоит из четырех основных модулей:

1. задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона;

2. векторные и матричные нормы;

3. итерационные методы;

4. методы подпространств Крылова.

Пособие предназначено для преподавания дисциплин в рамках магистерской образовательной программы “Математическое моделирование и компьютерная механика”.

Пособие также предназначено для студентов и аспирантов факультета математики, механики и компьютерных наук, специализирующихся в области математического моделирования, вычислительной математики и механики твердого деформируемого тела.

Пособие подготовлено в рамках гранта ЮФУ K-07-T-41.

1 Задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона 4

1.1 Решение уравнения −x 00 = f (t ) . . . . . . . . . . . . . . . 4

1.2 Решение уравнения Пуассона . . . . . . . . . . . . . . . . 6

2 Векторные и матричные нормы 11

2.1 Векторные нормы . . . . . . . . . . . . . . . . . . . . . . 11

2.2 Матричные нормы . . . . . . . . . . . . . . . . . . . . . . 13

2.3 Связь векторных и матричных норм . . . . . . . . . . . 15

3 Итерационные методы 19

3.1 Определения и условия сходимости итерационных методов 19

3.2 Метод простой итерации . . . . . . . . . . . . . . . . . . . 23

3.3 Метод Якоби . . . . . . . . . . . . . . . . . . . . . . . . . 24

3.4 Метод Гаусса-Зейделя . . . . . . . . . . . . . . . . . . . . 25

3.5 Метод последовательной верхней релаксации (SOR) . . . 26

3.6 Метод симметричной последовательной верхней релак-

сации (SSOR) . . . . . . . . . . . . . . . . . . . . . . . . . 27

4 Методы подпространств Крылова 30

4.1 Инвариантные подпространства . . . . . . . . . . . . . . 30

4.2 Степенная последовательность и подпространства Кры-

4.3 Итерационные методы подпространств Крылова . . . . . 33

Дополнительная литература 39

1 Задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона

Основным источником задач линейной алгебры для матриц большой размерности являются задачи, получаемые в результате дискретизации краевых задач математической физики. Далее рассмотрим два примера, иллюстрирующих особенности получаемых матричных задач.

1.1 Решение уравнения −x 00 = f (t )

Рассмотрим простейшую краевую задачу

Для дискретизации этой краевой задачи воспользуемся методом конечных разностей. Введем равномерную сетку на единичном отрезке

так, чтобы t ₀ = 0, t_n ₊₁ = 1. Используем обозначения

Для дискретизации второй производной воспользуемся центральной конечной разностью

которая аппроксимирует x 00 (t_i ) c точностью O (h 2 ). Тогда исходная краевая задача сводится к системе линейных алгебраических уравнений (СЛАУ) относительно

Эту СЛАУ можно записать также в матричном виде

Обратим внимание на следующие свойства матрицы A .

• A – разреженная матрица, она трехдиагональная;

• A – симметричная и, более того, положительно определенная. Это свойство она унаследовала от свойств оператора исходной краевой задачи;

• Структура A достаточно простая, ее элементы вычисляются по простым формулам. Следовательно, для ее хранения в памяти компьютера нет необходимости использовать типы данных, предназначенные для хранения заполненных матриц.

Обсудим размерность полученной СЛАУ. Предположим, что требуемая точность аппроксимации равна ² = 10 −6 . Поскольку ² ∼ h 2 , то

−3 , т.к. h ∼ √² . Т.е. требуемый шаг сетки нужно выбрать порядка 10 мы имеем матрицу размерности 10 3 × 10 3 . На практике, размерность должна быть выше, чтобы удовлетворить большей точности.

Рис. 1: Конечно-разностная сетка. Естественная нумерация узлов.

1.2 Решение уравнения Пуассона Рассмотрим более сложную краевую задачу

где u = u (x,y ) – неизвестная функция, f (x,y ) – известная, заданные на единичном квадрате (x,y ) ∈ Ω = [0, 1]×[0, 1]>, Γ = ∂ Ω – граница Ω. Введем на Ω равномерную сетку, так что координаты узлов даются формулами x_i = hi, y_i = hi, i = 0. N + 1, h = 1/ (N + 1).

Для дискретизации вторых производных в операторе Лапласа ∆ воспользуемся формулами для центральной конечной разности

Таким образом, исходная краевая задача сводится к СЛАУ

−u i −1,j + 4u i,j − u i +1,j − u i,j −1 − u i,j +1 = h 2f i,j (1) относительно u_i,j . Для того, чтобы свести ее к стандартному виду A x = b, необходимо преобразовать u_i,j к выражению с одним индексом, т.е. перенумеровать каким-то образом. Выбор нумерации влияет, вообще говоря, на структуру матрицы A .

Рассмотрим случай N = 3. Соответствующая сетка показана на рис. 1, где использована естественная нумерация внутренних узлов. Полые кружки соответствуют граничным узлам, в которых известно значение функции, а сплошные – внутренним.

Если преобразовать конечно-разностное уравнение (1) в матричное уравнение A x = b, вводя вектор неизвестных по правилу u 1, 1 = x 1, u 1, 2 = x 2, u 1, 3 = x 3, u 2, 1 = x 4. u 3, 3 = x 9,

Видно, что A является симметричной ленточной разреженной матрицей с диагональным преобладанием.

В результате нужно отметить, что в целом, матрица A обладает теми же свойствами, что и в случае одномерной, задачи, хотя ее структура может не быть ленточной, что зависит от способа нумерации узлов сетки

Обсудим размерность полученной СЛАУ. Предположим как и ранее, что требуемая точность аппроксимации равна ² = 10 −6 . Поскольку ² ∼ h 2 , то требуемый шаг сетки нужно выбрать порядка 10 −3 , т.к.

√ 3 × 10 3 = 10 6 . Таh ∼ ² . Число узлов здесь оказывается равным 10 кому же числу равно число неизвестных n . Таким образом, мы имеем матрицу размерности 10 6 × 10 6 .

Нетрудно догадаться, что если рассмотреть, не квадрат, а куб, то число неизвестных будет примерно равно n = 10 9 . В расчетной практике встречаются задачи, где нужно определять не одну функцию, а несколько. Например, в гидродинамике при учете теплопереноса имеем четыре скалярных неизвестных (три компоненты поля скорости и поле температуры). Если рассматривать конечно-разностную аппроксимацию этой задачи с точностью ² = 10 −6 , то получим размерность n = 4 · 10 9 .

Рассмотренные выше два примера показывают характерные источники задач линейной алгебры, приводящие к СЛАУ с большими разреженными матрицами. Естественно, что при решении таких СЛАУ необходимо развивать специальные методы вычислительной алгебры.

Рассмотрим другую нумерацию узлов, показанную на рис. 2. Здесь использовано так называемое красно-черное разбиение (или чернобелое). Вначале нумеруются узлы, сумма индексов которых – четное число, а потом узлы, сумма индексов которых дает нечетное число. Таким образом, вектор переменных вводится по правилу вектор неизвестных по правилу

– это красные неизвестные, а

Рис. 2: Конечно-разностная сетка. Красно-черное разбиение.

Соответствующая красно-черному разбиению матрица дается формулой

Видео:Решение систем линейных уравнений с помощью матрицСкачать

Решение разреженных СЛАУ больших размерностей средствами ManagedCuda в .NET

Зачастую в прикладных математических и компьютерных моделях возникает необходимость решать системы линейных алгебраических уравнений (СЛАУ). Как правило, на практике матрица в таких СЛАУ оказывается разреженной. Например, разреженные матрицы встречаются в моделях с конечно-разностными или конечно-элементными методами решения дифференциальных уравнений. Возникают сильно разреженные матрицы большой размерности при моделировании материальных и информационных потоков в крупных технологических сетях (системы газоснабжения и газораспределения, канализационные и теплоснабжающие системы, электросети и компьютерные сети и др.). Общим для технологических сетей является представление их моделей в виде графа, у которого матрица инциденций оказывается практически всегда сильно разреженной.

В статье будет рассказано о том, как ваш покорный слуга значительно повысил эффективность компьютерной модели расчета нестационарных течений газа в крупных системах газоснабжения произвольной конфигурации, благодаря применения библиотеки ManagedCuda и nVidia CUDA 7.0. Однако изложение будет вестись без привязки к конкретной предметной области.

Постановка задачи

Рассматривается классическая задача решения СЛАУ:
Ax=b
Здесь матрица A размером nxn, x — вектор неизвестных размером n, b — вектор известных свободных членов размером n.

Автор статьи занимается разработкой специализированного программно-вычислительного комплекса (ПВК) для моделирования и оптимизации нестационарных течений газа в системах газоснабжения. В решаемых мною задачах A является положительно определенным якобианом с диагональным преобладанием некоторой системы нелинейных уравнений. A получается в результате матричных преобразований матрицы инциденций графа системы газоснабжения и других матриц. В моих практических расчетах A обычно заполнена на 6-10%, остальное нули. Размер же ее зависит от размера конкретной системы газоснабжения и варьируется n от 10 до 1000.

Наш ПВК разрабатывается под .NET 4.0 на C#. Расчетный модуль и вся математика также разрабатывается на C#. Изначально для решения СЛАУ я написал собственную, доморощенную, библиотеку, не использующую технологию разреженных матриц. Для решения СЛАУ применял метод LU декомпозиции. И до поры меня все устраивало, пока я не начал заниматься задачей оптимизацией нестационарных режимов течения газа, где приходится методом динамического программирования осуществлять большое количество переборов значений управляющих параметров и, соответственно, много раз решать СЛАУ. Стандартный профилировщик Visual Studio показал, что в процессе выполнения программы около 40% затрат приходится на решение СЛАУ.

Именно в этот момент я понял, что пора что-то менять.

Математическая библиотека Math.Net Numerics

Проведя анализ имеющихся математических библиотек под .Net я решил остановиться на библиотеке Math.Net Numerics. Подробно ознакомиться с ней вы можете здесь.

Меня заинтересовали ее ключевые возможности:

Реализована технология разреженные матриц и векторов;
Имеются встроенные все необходимые вектор-матричные операции;
Присутствуют встроенные решатели;
Интуитивно понятный API.

Приведу листинг с примером решения СЛАУ средствами Math.Net Numerics:

Как видно, все очень элегантно выглядит, но практически сразу меня настигло разочарование — встроенный решатель Math.Net Numerics работал значительно медленнее моего. Меня это совершенно не устроило, однако претензии к реализованным в библиотеке вектор-матричным операциям не столь существенные. Поэтому полностью отказываться от Math.Net Numerics я не стал, оставив код, где производится работа с векторами и матрицами.

Но тут мне вспомнился весьма удачный опыт коллег по аспирантуре, которые для решения задач подземной гидродинамики использовали графические процессоры. В распоряжении у меня имеется ноутбук с видеокартой nVidia GeeForce GT 540M с 2 GB памяти и поддержкой технологии CUDA. Было принято решение попробовать эту технологию на деле, о чем теперь не жалею.

Библиотека ManagedCuda

О технологии CUDA на этом сайте имеется большое количество материала, поэтому любопытный читатель без особого труда его найдет. Я же остановлюсь на том, как решал поставленную перед собой задачу.

Меня заинтересовала библиотека cuSPARSE. При первом знакомстве с ней я наткнулся на проблемы:

Непосредственная работа с библиотекой возможна только через C/C++. Конечно, проблема решится, если использовать качественный враппер, который очень не хотелось писать. По результатам поиска был найден CUDA-враппер для .Net под названием Cudafy.
cuSPARCE позволяет решать СЛАУ с треугольными матрицами, а в моем случае матрицы таковыми не являются. Однако cuSPARSE содержит методы факторизации матриц, приводящие их к треугольной форме (метод LU факторизации, разложение Холецкого). Однако в API Cudafy отсутствовали соответствующие методы, поэтому от Cudafy пришлось отказаться.

После продолжения поиска я открыл для себя библиотеку ManagedCuda, которая является высокоуровневой оберткой над CUDA API. Все её возможности я перечислять не буду — их можно найти на официальном сайте, но остановлюсь на том, как можно, используя Math.Net Numerics и ManagedCuda, элегантно и эффективно решать СЛАУ.

Идея заключается в использовании SparseMatrix из Math.Net Numerics для формирования и хранения разреженной матрицы в формате CSR, который принимают на вход cuSPARSE и ManagedCuda. Далее приводится листинг соответствующей программы:

Вычислительный эксперимент: анализ временных затрат на решению СЛАУ различными технологиями

Дабы не утомлять читателя сухим текстом и листингами программ, рассмотрим результаты расчетов СЛАУ размерностей от 50 до 500 с помощью различных технологий:

Доморощенный решатель, написанный автором статьи. Назовем его Mani.Net.
Стандартный решатель библиотеки Math.Net Numerics.
Метод LU декомпозиции библиотеки ManagedCuda.

Матрица A заполняется на 10% случайным образом.

Рисунок наглядно демонстрирует, почему мне пришлось отказаться от Math.Net Numerics для решения СЛАУ.
Отметим, при размерности матрицы равной 500 моему собственному решателю (Mani.Net) потребовалось 1170 мс, Math.Net Numerics — 12968 мс, ManagedCuda — 70 мс.

Заключение

Следует ожидать в комментариях замечания, мол де не на всех машинах есть GPU nVidia с поддержкой CUDA. Действительно, это так. Поэтому наше приложение настроено на две конфигурации компиляции: с собственной библиотекой решения СЛАУ и с ManagedCuda.

Насчет Mani.Net отмечу, что это не реклама моей собственной библиотеки. Найти ее нигде невозможно и никому её я передавать не буду. Нет, я не жадный. Мне стыдно за код.

Спасибо за прочтение статьи! Буду рад узнать о вашем мнении и замечаниях в комментариях.