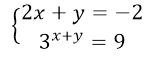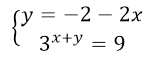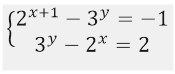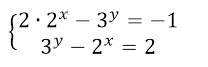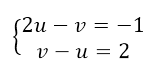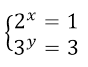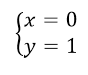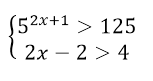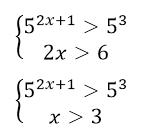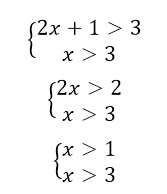Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений.
Решить системы уравнений:
Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.
Решаем (2) -ое уравнение полученной системы:
2 х +2 x +2 =10, применяем формулу: a x + y =a x ∙a y .
2 x +2 x ∙2 2 =10, вынесем общий множитель 2 х за скобки:
2 х (1+2 2 )=10 или 2 х ∙5=10, отсюда 2 х =2.
2 х =2 1 , отсюда х=1. Возвращаемся к системе уравнений.
Ответ: (1; 2).
Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5.
Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.
Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.
Находим х=2 и это значение подставляем вместо х во второе уравнение системы.
Находим у.
Ответ: (2; 1,5).
Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.
Решаем (2) -ое уравнение системы.
v 2 +63v-64=0. Подберем корни по теореме Виета, зная, что: v1+v2=-63; v1∙v2=-64.
Получаем: v1=-64, v2=1. Возвращаемся к системе, находим u.
Так как значения показательной функции всегда положительны, то уравнения 4 x = -1 и 4 y = -64 решений не имеют.
Представляем 64 и 1 в виде степеней с основанием 4.
Приравниваем показатели степеней и находим х и у.
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- Системы показательных уравнений и неравенств
- Способы решения систем уравнений
- Системы показательных уравнений
- Готовые работы на аналогичную тему
- Системы показательных неравенств
- 📺 Видео
Видео:10 класс. Алгебра. Системы показательных уравнений.Скачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Системы показательных уравнений и неравенств
Вы будете перенаправлены на Автор24
Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Способы решения систем уравнений
Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.
Существуют четыре основных способа решения систем уравнений:
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.
Видео:Решение систем уравнений методом подстановкиСкачать

Системы показательных уравнений
Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.
Решение систем показательных уравнений будем рассматривать на примерах.
Решить систему уравнений
Решение.
Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.
Подставим $y$ во второе уравнение:
Ответ: $(-4,6)$.
Решить систему уравнений
Решение.
Данная система равносильна системе
Применим четвертый метод решения уравнений. Пусть $2^x=u (u >0)$, а $3^y=v (v >0)$, получим:
Решим полученную систему методом сложения. Сложим уравнения:
Тогда из второго уравнения, получим, что
Возвращаясь к замене, получил новую систему показательных уравнений:
Ответ: $(0,1)$.
Готовые работы на аналогичную тему
Видео:Показательная функция. 11 класс.Скачать
Системы показательных неравенств
Cистемы неравенств, состоящие из показательных уравнений, называются системой показательных неравенств.
Решение систем показательных неравенств будем рассматривать на примерах.
Решить систему неравенств
Решение:
Данная система неравенств равносильна системе
Для решения первого неравенства вспомним следующую теорему равносильности показательных неравенств:
Теорема 1. Неравенство $a^ >a^ $, где $a >0,ane 1$ равносильна совокупности двух систем
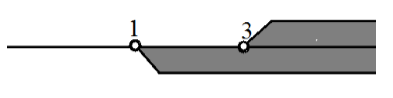
Изобразим оба решения на числовой прямой (рис. 11)
Рисунок 11. Решение примера 3 на числовой прямой
Ответ: $(3,+infty )$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 22 03 2021
📺 Видео
Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Показательные уравнения. 11 класс.Скачать

Показательные неравенства и их системы. Вебинар | МатематикаСкачать

Как решать такие системы показательных уравненийСкачать

Алгебра 10 класс (Урок№22 - Показательные уравнения. Системы показательных уравнений.)Скачать

Как решать системы показательных уравнений. Урок№ 27Скачать

Это просто! Как решать Показательные Неравенства?Скачать

СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ системы показательных неравенствСкачать

Система уравнений с показательными и гармоническими функциямиСкачать

11 класс, 11 урок, Показательная функция, её свойства и графикСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

11 класс, 12 урок, Показательные уравненияСкачать

Как решать Показательные Уравнения? (часть 2)Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

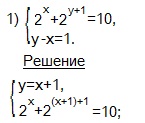
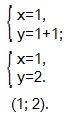
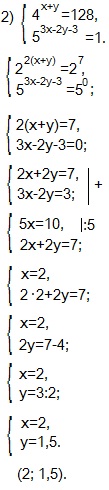
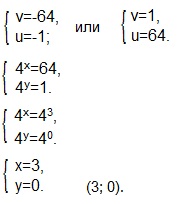










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);