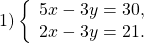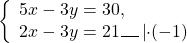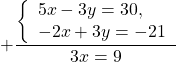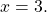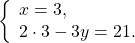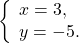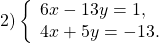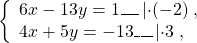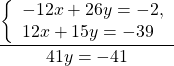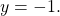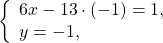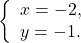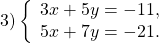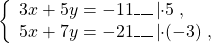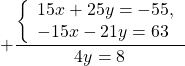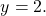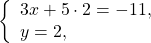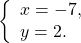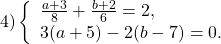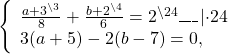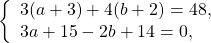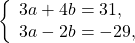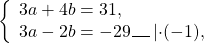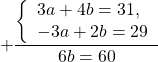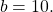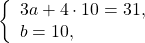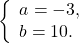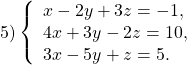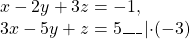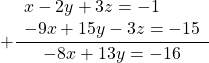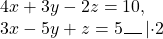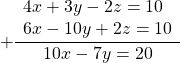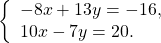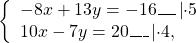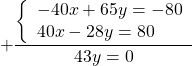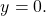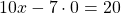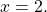Рассмотрим конкретные примеры решения систем линейных уравнений способом сложения.
Ищем наибольший общий делитель коэффициентов при каждой из переменных (коэффициенты берем со знаком «+»).
Наименьшее общее кратное коэффициентов при x — НОК(5;2)=10, при y — НОК(3;3)=3.
Проще работать с y, поскольку для получения перед y противоположных чисел достаточно умножить любое из уравнений на -1. Проще умножить на -1 второе уравнение системы (в этом случае после сложения уравнений коэффициент при x — положительное число).
Теперь подставим x=3 в любое из уравнений системы, например, во второе:
Решаем это уравнение:
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
НОК(6; 4)=12, НОК(13; 5)=65. Проще работать с коэффициентами перед x.
Чтобы получить перед иксами противоположные числа, первую систему умножим на -2, вторую — на 3
и сложим почленно левые и правые части уравнений:
Подставляем y= -1 в первое уравнение системы и находим x:
НОК(3; 5)=15, НОК(5; 7)=35. Проще получить противоположные числа перед x.
Для этого умножим первое уравнение системы на 5, второе — на -3:
и сложим почленное левые и правые части полученных уравнений:
Подставляем y=2 в первое уравнение системы и находим x:
Прежде чем применить способ сложения, данную систему следует упростить. Умножим первое уравнение на наименьший общий знаменатель дробей, во втором раскроем скобки:
Получили систему линейных уравнений с двумя переменными. Для решения её способом сложения достаточно умножить второе уравнение на -1 и сложить почленно левые и правые части уравнений:
Подставляем найденное значение b в первое уравнение системы (линейных уравнений):
Систему линейных уравнений с тремя переменными можно решить, сначала исключив одно из неизвестных, а затем — другое.
В данной системе проще всего исключить переменную z.
К первому уравнению прибавим третье, умноженное на -3:
Ко второму уравнению прибавим третье, умноженное на 2:
Получили систему линейных уравнений с двумя переменными:
НОК(8;10)=40, НОК(13; 7)=91. Проще работать с x:
Подставив полученные значение y во второе уравнение системы с двумя переменными, найдём x:
Подставив значения y и x в третье уравнение системы с тремя переменными, найдём z:
- Решение системы линейных уравнений методом сложения
- Алгоритм решения системы линейных уравнений методом сложения
- Примеры
- Как решать систему уравнений
- Основные понятия
- Линейное уравнение с двумя переменными
- Система двух линейных уравнений с двумя переменными
- Метод подстановки
- Пример 1
- Пример 2
- Пример 3
- Метод сложения
- Система линейных уравнений с тремя переменными
- Решение задач
- Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
- Задание 2. Как решать систему уравнений способом подстановки
- Задание 3. Как решать систему уравнений методом сложения
- Задание 4. Решить систему уравнений
- Задание 5. Как решить систему уравнений с двумя неизвестными
- 📺 Видео
Видео:Решение систем уравнений методом сложенияСкачать

Решение системы линейных уравнений методом сложения
Алгоритм решения системы линейных уравнений методом сложения
- Умножить обе части одного или обоих уравнений так, чтобы коэффициенты при одной из переменных стали противоположными (или равными) числами.
- Сложить (или отнять) уравнения, чтобы избавиться от одной из переменных.
- Решить второе уравнение относительно выраженной переменной.
- Решить полученное уравнение с одной переменной.
- Найти вторую переменную.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Умножаем первое уравнение на 2
Отнимаем от первого уравнения второе:
Находим y из первого уравнения:
В последовательной записи:
$$ <left< begin 3x+y = 5 | times 2 \ x+2y = 5 end right.> Rightarrow (-) <left< begin 6x+2y = 10 \ x+2y = 5 end right.> Rightarrow <left< begin 5x = 5 \ x+2y = 5 end right.> Rightarrow <left< begin x = 1 \ y = 5-3x = 2 end right.> $$
Примеры
Пример 1. Решите систему уравнений методом сложения:
$ а) <left< begin 5x-4y = 3 | times 2 \ 2x-3y = 4 | times 5 end right.> Rightarrow <left< begin 10x-8y = 6 \ 10x-15y = 20 end right.> Rightarrow <left< begin 7y = -14 \ 2x-3y = 4 end right.> Rightarrow <left< begin x = frac = -1 \ y=-2 end right.> $
$ б) <left< begin 4x-3y = 7 | times 3 \ 3x-4y = 0 | times 4 end right.> Rightarrow (-) <left< begin 12x-9y = 21 \ 12x-16y = 0 end right.> Rightarrow <left< begin 7y = 21 \ x = frac y end right.> Rightarrow <left< begin x = 4 \ y = 3 end right.> $
$ в) <left< begin 5a-4b = 9 | times 2 \ 2a+3b = -1 | times 5 end right.> Rightarrow (-) <left< begin 10a-8b = 18 \ 10a+15b = -5 end right.> Rightarrow <left< begin -23b = 23 \ a = frac end right.> Rightarrow <left< begin a = 1 \ b = -1 end right.> $
$ г) <left< begin 7a+4b = 5 \ 3a+2b = 1 | times (-2) end right.> Rightarrow (+) <left< begin 7a+4b = 5 \ -6a-4b = -2 end right.> Rightarrow <left< begin a = 3 \ b = frac end right.> Rightarrow <left< begin a = 3 \ b = -4 end right.>$
Пример 2. Найдите решение системы уравнений:
$$а) <left< begin frac-y = 7 \ 3x+ frac = 9 | times 2end right.> Rightarrow (+) <left< begin frac -y = 7 \ 6x+y = 18 end right.> Rightarrow <left< begin 6 frac x = 25 \ y = 18-6xend right.> Rightarrow $$
$$Rightarrow <left< begin x = 25: frac = 25 cdot frac = 4 \ y = 18-6 cdot 4 = -6 end right.> $$
$ в) <left< begin 3(5x-y)+14 = 5(x+y) \ 2(x-y)+9 = 3(x+2y)-16 end right.> Rightarrow <left< begin 15x-3y+14 = 5x+5y \ 2x-2y+9 = 3x+6y-16 end right.> Rightarrow $
$ г) <left< begin 5-3(2x+7y) = x+y-52 \ 4+3(7x+2y) = 23x end right.> Rightarrow <left< begin 5-6x-21y = x+y-52 \ 4+21x+6y = 23x end right.> Rightarrow <left< begin 7x+22y = 57 \ 2x-6y = 4 |:2 end right.>$
$$ Rightarrow <left< begin 7x+22y = 57 \ x-3y = 2 | times 7 end right.> Rightarrow (-) <left< begin 7x+22y = 57 \ 7x-21y = 14 end right.> Rightarrow <left< begin 43y = 43 \ x = 3y+2 end right.> Rightarrow <left< begin x = 5 \ y = 1 end right.>$$
Пример 3*. Найдите решение системы уравнений:
Введём новые переменные: $ <left< begin a = frac \ b = frac end right.> $
Перепишем систему и найдём решение для новых переменных:
$$ <left< begin2a+3b = 1| times 3 \ 3a-5b = 11 | times 2 end right.> Rightarrow (-) <left< begin 6a+9b = 3 \ 6a-10b = 22 end right.> Rightarrow <left< begin 19b = -19 \ a = frac end right.> Rightarrow <left< begin a = 2 \ b = -1 end right.> $$
Видео:Решение систем уравнений методом сложенияСкачать

Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Видео:7 класс, 39 урок, Метод алгебраического сложенияСкачать

Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Видео:Решение систем уравнений методом сложенияСкачать

Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Видео:Решение систем уравнений. Способ сложенияСкачать

Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Видео:6 способов в одном видеоСкачать

Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
📺 Видео
МЕТОД СЛОЖЕНИЯ | 7 класс алгебра | решение систем уравненийСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Алгебра 7 класс. 28 октября. Решаем систему уравнений методом сложения #2Скачать

Решение систем уравнений методом сложения. Алгебра 9 класс.Скачать

Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Решение систем линейных уравнений методом сложения - 7 класс. Как решать систему уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Видеоурок СПОСОБ СЛОЖЕНИЯ 7 КЛАСС.Скачать