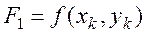Решение получаем с помощью калькулятора Решение СЛАУ методом итераций .
Видео:4.2 Решение систем нелинейных уравнений. МетодыСкачать

Достаточное условие сходимости метода простых итераций
Прежде чем применять метод итераций, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы. Если при этом условие все таки не выполняется, то иногда удается обеспечить сходимость метода с помощью следующего метода.
Пусть дана система Ax = b. Преобразуем ее к виду: x= Qx + c
где Q = E — D•A, c = D•b
Здесь D — некоторая матрица. Нам необходимо подобрать такую матрицу D, чтобы выполнялось условие |Q| 0 =β, тогда:
x 1 =b — a x 0
x 2 =b — a x 1
.
x k+1 =b — a x k
Для нашей задачи достаточное условие сходимости выполняется.
| 10 | 2 | -1 |
| -2 | -6 | -1 |
| 1 | -3 | 12 |
Приведем к виду:
x1=0.5-(0.2x2-0.1x3)
x2=-4.07-(0.33x1+0.17x3)
x3=3-(0.0833x1-0.25x2)
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.5 — 0 • 0.2 — 0 • (-0.1)=0.5
x2=-4.07 — 0 • 0.33 — 0 • 0.17=-4.07
x3=3 — 0 • 0.0833 — 0 • (-0.25)=3
N=2
x1=0.5 — (-4.07) • 0.2 — 3 • (-0.1)=1.61
x2=-4.07 — 0.5 • 0.33 — 3 • 0.17=-4.74
x3=3 — 0.5 • 0.0833 — (-4.07) • (-0.25)=1.94
N=3
x1=0.5 — (-4.74) • 0.2 — 1.94 • (-0.1)=1.64
x2=-4.07 — 1.61 • 0.33 — 1.94 • 0.17=-4.93
x3=3 — 1.61 • 0.0833 — (-4.74) • (-0.25)=1.68
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | e1 | e2 | e3 |
| 0 | 0 | 0 | 0 | |||
| 1 | 0.5 | -4.07 | 3 | 0.5 | 4.07 | 3 |
| 2 | 1.61 | -4.74 | 1.94 | 1.11 | 0.67 | -1.06 |
| 3 | 1.64 | -4.93 | 1.68 | 0.0274 | 0.19 | -0.26 |
| 4 | 1.65 | -4.9 | 1.63 | 0.013 | -0.0341 | -0.051 |
| 5 | 1.64 | -4.89 | 1.64 | -0.0119 | -0.00416 | 0.00744 |
| 6 | 1.64 | -4.89 | 1.64 | -8.8E-5 | -0.00273 | 0.00203 |
| 7 | 1.64 | -4.89 | 1.64 | -0.000343 | 0.00031 | 0.000691 |
Ответ: x1=1.64, x2=-4.89, x3=1.64
Пример №2 . Решить систему уравнений Ax = b с точностью 0.05 методами: 1) простой итерации; 2) Зейделя. Указание. Для обеспечения выполнения достаточного условия сходимости воспользоваться перестановкой строк в исходной системе уравнений.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Итерационные методы решения системы линейных алгебраических уравнений
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Видео:6 способов в одном видеоСкачать

Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Видео:Матричный метод решения систем уравненийСкачать

Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = — a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε
В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) — x ( n ) ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 — 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) — x ( n ) ε
Далее вычисляем нормы разности векторов:
x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Видео:Решение систем уравнений методом сложенияСкачать

Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Видео:Решение системы уравнений методом ГауссаСкачать

Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x — τ ( A x — b ) , τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .
Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .
Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Приближённые методы решения СЛАУ
Лекция 1
Приближённые методы решения СЛАУ
А) Метод простых итераций.(Метод последовательных приближений).
Пусть дана система n линейных уравнений с n неизвестными:

или 



Задаются произвольно n-чисел – нулевое приближение искомой функции.
Далее подставляем в правую часть системы (1) нулевое приближение и
находим первое приближение.
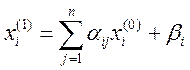

Затем по 1-ому приближению находят 2-ое, 3-е и т.д.
В результате для k-ого приближения получаем формулу:


Таким образом мы получили последовательность векторов
Х (0) ,Х (1) ,…, Х (К) , к=1,2,…
Если любая из таких последовательностей <Хi (к) > сходится некоторому пределу 

В равенстве (2’) перейдем к пределу при k→∞ при замене хi на сi.
Теорема(достаточные условия сходимости простой итерации):
Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):
а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:
б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:
в) Если сумма всех элементов в квадрате меньше 1.
Если выполняется хотя бы одно, тогда справедливы утверждения:
1)система (1) имеет единственное решение (С1. Сn);
2)последовательность 



3)для приближенного равенства верны оценки (x1 ( k ) ,…xn ( k ) ) 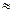
а’) есливыполняется условие а), то

б’) если выполняется условие б), то
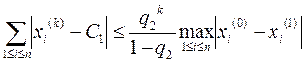
в’) если выполняется условие в), то

Замечания:
1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. 

2)остановка вычислений производной по заданной величине абсолютной погрешности 
Б) Метод Зейделя.
Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного хi (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х1, х2,…, хi-1
Рассмотрим систему: 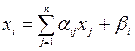
Пусть матрица α удовлетворяет одному из условий теоремы:
Если, а) 
Прямой ход.
Это основной этап решения системы уравнений с помощью метода Гаусса. Его суть состоит в приведении исходной расширенной матрицы системы к верхнетреугольной матрице с помощью эквивалентных преобразований (добавление к строке любой линейной комбинации других строк и перестановка строк, т.е. уравнений). Формулы прямого хода соответствуют последовательному выражению переменных из уравнений и подстановке их в последующие уравнения, т.е. их фактическому исключению из последующих уравнений системы. При этом шагом считается исключение одной переменной из всех последующих уравнений системы.
Рассмотрим k-ый шаг прямого хода. На k-ом шаге матрица системы имеет вид:
Осталось n-k+1 неизвестных. Чтобы удалить х(k) из последней строчки, например, надо из нее вычесть k-ую строчку с таким коэффициентом, чтобы получить на месте аnk ноль. Для этого коэффициент должен быть равен cnk=ank/akk. Элемент аkk называется разрешающим элементом k-ого шага и должен быть отличен от 0.
Формулы прямого хода
cmk=amk/akk где 1

Лекция 2.
Выбор шага
1. Пусть требуется вычислить интеграл с точностью ε. Используя формулу соответствующего остаточного члена R, выбирают h таким образом, чтобы выполнялось неравенство 
2. Двойной пересчёт. ( Правило Рунге).
Лекция 4
ЧИСЛЕННОЕ РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удаётся найти точно. Поэтому большое значение приобретают способы приближённого нахождения корней уравнения и оценки степени их точности.
Процесс нахождения приближённых значений корней уравнения:
f(x) = 0, (1)
где функция f(x) определена и непрерывна в некотором конечном или
бесконечном интервале a n раз. Таким образом, число итераций n в данном методе зависит от предварительно заданной точности ε и от длины исходного отрезка и не зависит от вида функции f(x). Это является важным преимуществом метода половинного деления по сравнению с другими методами. Метод, однако, медленно сходится при задании высокой точности расчёта.
Метод хорд.
Пусть на отрезке [a,b] функция f(x) непрерывна и принимает на концах отрезка значения разных знаков, а производные f ′(x) и f ″(x) сохраняют постоянный знак на интервале (a,b). Тогда возможны четыре случая расположения дуги кривой (рис.4).


Рис.4.
В методе хорд за очередное приближение берём точку пересечения с осью Х прямой (рис.5), соединяющей точки (a,f(a)) и (b,f(b))
Причём одна из этих точек фиксируется − та, для которой знаки f(x) и f ″(x) одинаковы.
Для рис.5 неподвижным концом хорды является х =a.
Уравнение хорды АВ:
Точка пересечения хорды с осью Х (у=0): 
Теперь корень находится на отрезке [a,c1]. Заменяем b на с1.
Рис.5. Иллюстрация метода хорд.
Применяя метод хорд к этому отрезку, получим:

Продолжим и т.д., получим: 
│сn+1 − cn│ 0, то приближённое значение корня находят по формуле (2), если f′(x)∙f″(x) ( n ) ) = 0 или 
Определение: Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
у′-2ху 3 +5=0—— уравнение первого порядка,
у″+ky′-by-sinx=0—— уравнение второго порядка.
Задача Коши (для уравнения первого порядка):
у′ = f(x, y) (1) найти решение y = y(x),
удовлетворяющее начальному условию: у(х0)=у0. (1*).
Т.е. найти интегральную кривую, проходящую через точку М(х0, у0).
Если f(x,y) непрерывна в области R: |x-x0| ( n ) =f(x,y,y′,…,y ( n -1) ) задача Коши состоит в нахождении решения у = у(х), удовлетворяющего начальным условиям:
у(х0) = у0, у′(х0) = у′0, …, у ( n -1) (x0) = y ( n -1) 0 ― заданные числа.
Функция у = f(x, C1, C2,…, Cn), где С1,…, Сn― произвольные постоянные, называется общим решением ОДУ или общим интегралом.
Эти постоянные можно определить с помощью начальных условий. Решение ДУ при заданных начальных условиях называется его частным решением.
Определение: задача называется краевой, если указывается интервал интегрирования [a,b] и ставятся дополнительные условия для значений функции у и её производных на концах этого интервала.
Процесс познания закономерностей и стремление создать детальную картину исследуемых явлений приводит к более сложной количественной оценке, отражающей эти явления, а именно к функции многих переменных, зависящих как от пространственных координат, так и от времени u = f(x1, x2,…, xn, t).
Определение: Дифференциальным уравнением с частными производными называется уравнение, связывающее независимую переменные х1, х2, …, хn, t, искомую функцию
u = f (х1, х2, …, хn, t) и её частные производные:

Постановка задачи.
Дано дифференциальное уравнение первого порядка: у′ = f(x,y) (1).
Требуется найти решение этого уравнения на отрезке [x0, xmax], удовлетворяющее начальным условиям: у(х0) = у0 (2).
В вычислительной практике более предпочтительным являются численные методы нахождения приближённого решения в фиксированных точках: х0 1 и b0 = 0 ― явными многошаговыми.
― при r > 1 и b0 ≠ 0 ― неявными многошаговыми.
Многошаговость нарушает однородность вычислительного процесса, используя для получения недостающей информации другие вычислительные схемы ( например, одношаговые).
А) Метод Эйлера.
| х | x0 | x1 | … | хn |
| y | y0 | y1 | … | yn |
Для решение Д.У.(1) с Н.У. (2) на отрезке [x0, xmax] по методу Эйлера, таблица приближённых значений у(х) для равноотстоящих узлов:
Абсолютная погрешность формулы (4) на каждом шаге имеет порядок h 2

Формула (4) означает, что на отрезке [xk, xk+1] интегральная кривая y = y(x) приближённо заменяется прямолинейным отрезком, выходящим из точки М(хk;уk) с угловым коэффициентом f(хk;уk). В качестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точках М0(х0;у0), М1(х1;у1),…, Мn(хn;уn). Первое звено касается истинной интегральной кривой в точке М0(х0;у0).
Метод Эйлера может быть применён к решению системы ОДУ и ДУ высших порядков. Последние должны быть предварительно приведены к системе ОДУ первого порядка.
Пусть задана система ОДУ первого порядка: 
Приближённые значения у(хi) ≈ yi, z(хi) ≈ zi вычисляются по формулам:

Метод Эйлера обладает двумя существенными недостатками:
1) малой точностью (метод первого порядка точности);
2) систематическое накопление ошибок.
В) Модификации метода Эйлера.
1 ый усовершенствованный метод Эйлера.
Сначала вычисляют промежуточные значения:

А затем полагают: 
2 o й усовершенствованный метод Эйлера.
Сначала определяют «грубые приближения»: 
И приближённо полагают: 
Локальная погрешность на i-ом шаге: 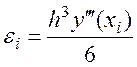

С.) Метод Рунге-Кутта. (4 го порядка)
Наиболее знаменитым из методов Рунге-Кутта является классический метод 4 го порядка


Грубая оценка погрешности (двойной просчёт): 
Где у(хi) – точное решение, у * i – приближённое решение с шагом h/2, yi – … с шагом h .
Для оценки правильности выбора шага h используют равенство:
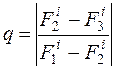
q должно равняться нескольким сотым, иначе h уменьшается.
D). Метод Рунге–Кутта 3-го порядка
Многошаговые методы.
(используют информацию о нескольких предыдущих точках)
Д ) Алгоритм Адамса.
Пусть дано дифференциальное уравнение: у′ = f(x, y) (1)
с начальными условиями: у(х0) = у0 (1*)
Требуется найти решение уравнения (1) на отрезке [a,b].
Разобьём отрезок [a,b] на n равных частей точками хi = х0 + ih (i =0, 1, …, n).
1 ый этап: стартовая процедура. Используют какой-либо одношаговый метод того же порядка точности до тех пор, пока не будет получено достаточно значений для работы многошагового метода.
2 ой этап: рекурсивной процедуры. Определение: уk, yk+1,…, yn основано на интегрировании интерполяционного многочлена Ньютона.
Рабочие формулы явных методов Адамса (2-го, 3-го, 4-го порядков).
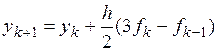


Формулы (2)-(4) называются экстраполяционными и на практике используются в качестве прогноза.
Для улучшения точности или коррекции результата применяют неявные методы (используют ещё ненайденные значения: уk+1, yk+2,…).



Формулы (5)-(7) называются интерполяционными.
Для грубой оценки точности (двойной просчёт):
Лекция 1
Приближённые методы решения СЛАУ
А) Метод простых итераций.(Метод последовательных приближений).
Пусть дана система n линейных уравнений с n неизвестными:

или 



Задаются произвольно n-чисел – нулевое приближение искомой функции.
Далее подставляем в правую часть системы (1) нулевое приближение и
находим первое приближение.
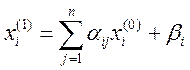

Затем по 1-ому приближению находят 2-ое, 3-е и т.д.
В результате для k-ого приближения получаем формулу:


Таким образом мы получили последовательность векторов
Х (0) ,Х (1) ,…, Х (К) , к=1,2,…
Если любая из таких последовательностей <Хi (к) > сходится некоторому пределу 

В равенстве (2’) перейдем к пределу при k→∞ при замене хi на сi.
Теорема(достаточные условия сходимости простой итерации):
Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):
а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:
б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:
в) Если сумма всех элементов в квадрате меньше 1.
Если выполняется хотя бы одно, тогда справедливы утверждения:
1)система (1) имеет единственное решение (С1. Сn);
2)последовательность 



3)для приближенного равенства верны оценки (x1 ( k ) ,…xn ( k ) ) 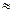
а’) есливыполняется условие а), то

б’) если выполняется условие б), то
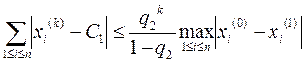
в’) если выполняется условие в), то

Замечания:
1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. 

2)остановка вычислений производной по заданной величине абсолютной погрешности 
Б) Метод Зейделя.
Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного хi (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х1, х2,…, хi-1
Рассмотрим систему: 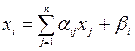
Пусть матрица α удовлетворяет одному из условий теоремы:
Если, а) 
💡 Видео
Решение систем уравнений методом подстановкиСкачать

Численные методы. Лекция 1. Решение систем линейных уравнений. Метод ГауссаСкачать

Метод касательных (метод Ньютона)Скачать

Метод ЭйлераСкачать

Метод простой итерации Пример РешенияСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Базисные решения систем линейных уравнений (03)Скачать

Метод Гаусса решения систем линейных уравненийСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

10 Численные методы решения нелинейных уравненийСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение систем уравнений методом сложенияСкачать