Решение систем уравнений подготовка к огэ

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Линейные уравнения

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Линейные уравнения

Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .

Примеры линейных уравнений:

1. 3 x = 2

1. 2 7 x = − 5

Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.

Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.

Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .

Примеры решения линейных уравнений:

1. 2 x + 1 = 2 ( x − 3 ) + 8

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду a x = b :

Для начала раскроем скобки:

2 x + 1 = 4 x − 6 + 8

В левую часть переносятся все слагаемые с x , в правую – числа:

Теперь поделим левую и правую часть на число ( -2 ) :

− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5

Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

x 2 + 3 x − 8 = x − 1

Это уравнение не является линейным уравнением.

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

1. 2 x − 4 = 2 ( x − 2 )

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2 x − 2 x = − 4 + 4

И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2 x − 4 = 2 x − 16

2 x − 2 x = − 16 + 4

В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.

Видео:Урок 4. Уравнения и системы уравнений. Алгебра ОГЭ . Вебинар | МатематикаСкачать

Квадратные уравнения

Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .

Алгоритм решения квадратного уравнения:

1. Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
2. Выписать, чему равны в числах коэффициенты: a = … b = … c = …
3. Вычислить дискриминант по формуле: D = b 2 − 4 a c
4. Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
5. Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
6. Если D 0, решений нет: x ∈ ∅

Примеры решения квадратного уравнения:

1. − x 2 + 6 x + 7 = 0

a = − 1, b = 6, c = 7

D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64

D > 0 – будет два различных корня:

x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7

Ответ: x 1 = − 1, x 2 = 7

a = − 1, b = 4, c = − 4

D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0

D = 0 – будет один корень:

x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2

a = 2, b = − 7, c = 10

D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31

D 0 – решений нет.

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Разложение квадратного трехчлена на множители

Квадратный трехчлен можно разложить на множители следующим образом:

a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )

где a – число, коэффициент перед старшим коэффициентом,

x – переменная (то есть буква),

x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.

Если квадратное уравнение имеет только один корень , то разложение выглядит так:

a x 2 + b x + c = a ⋅ ( x − x 0 ) 2

Примеры разложения квадратного трехчлена на множители:

1. − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7

− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )

1. − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2

− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2

Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:

• c = 0 ⇒ a x 2 + b x = x ( a x + b )

• b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.

Видео:Решение систем уравнений. Подготовка к ЕГЭ и ОГЭСкачать

Дробно рациональные уравнения

Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .

Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f ( x ) g ( x ) = 0

ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

1. Привести выражение к виду f ( x ) g ( x ) = 0 .
2. Выписать ОДЗ: g ( x ) ≠ 0.
3. Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
4. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.

Решение:

Будем действовать в соответствии с алгоритмом.

1. Привести выражение к виду f ( x ) g ( x ) = 0 .

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x 2 − 4 2 − x − 1 2 − x = 0

x 2 − 4 2 − x − 2 − x 2 − x = 0

x 2 − 4 − ( 2 − x ) 2 − x = 0

x 2 − 4 − 2 + x 2 − x = 0

x 2 + x − 6 2 − x = 0

Первый шаг алгоритма выполнен успешно.

Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2

1. Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:

x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.

a = 1, b = 1, c = − 6

D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25

D > 0 – будет два различных корня.

x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3

1. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Корни, полученные на предыдущем шаге:

Значит, в ответ идет только один корень, x = − 3.

Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Системы уравнений

Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.

Пример системы уравнений

Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.

Существует два метода решений систем линейных уравнений:

1. Метод подстановки.
2. Метод сложения.

Алгоритм решения системы уравнений методом подстановки:

1. Выразить из любого уравнения одну переменную через другую.
2. Подставить в другое уравнение вместо выраженной переменной полученное значение.
3. Решить уравнение с одной неизвестной.
4. Найти оставшуюся неизвестную.

Решить систему уравнений методом подстановки

Решение:

1. Выразить из любого уравнения одну переменную через другую.

1. Подставить в другое уравнение вместо выраженной переменной полученное значение.

1. Решить уравнение с одной неизвестной.

3 ( 8 − 2 y ) − y = − 4

y = − 28 − 7 = 28 7 = 4

1. Найти оставшуюся неизвестную.

x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0

Ответ можно записать одним из трех способов:

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Решить систему уравнений методом сложения

Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .

Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )

− 3 x − 6 y + 3 x − y = − 24 − 4

y = − 28 − 7 = 28 7 = 4

Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.

Ответ можно записать одним из трех способов:

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.

Видео:ОГЭ Задания 20 Решение систем уравнений способом алгебраического сложенияСкачать

Решение систем уравнений при подготовке к ОГЭ .

Урок обобщения, систематизации и контроля знаний при решении систем уравнений в 9 классе. В ходе урока предполагается, что каждый учащийся достигнет определенного уровня понимания материала, поэтому материал разработан дифференцированно.

Просмотр содержимого документа
«Решение систем уравнений при подготовке к ОГЭ .»

Подготовка к ОГЭ

Решение систем уравнений

Денисюк Галина Михайловна

Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит Абу-р-Райхан ал-Бируни

Цель: повторить основные понятия по теме, решать системы равнений.

Помнить! Нельзя решить задание, не зная свойств, определений понятий, которые указаны в задании.

1. Выделить темы, имеющие место в задании.

2. Найти в учебнике, справочной литературе сведения по данной теме.

4. Приступить к решению .

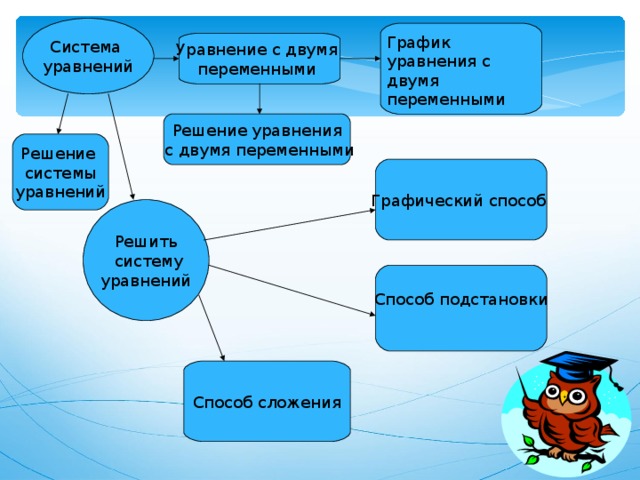
График уравнения с двумя переменными

Уравнение с двумя

с двумя переменными

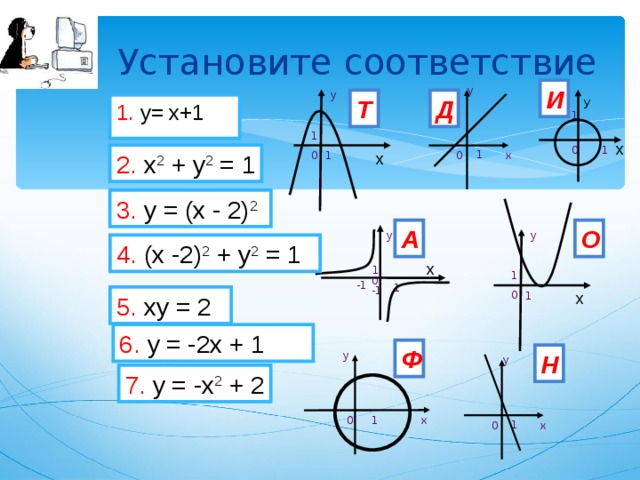
4. (х -2) 2 + у 2 = 1

Диофант Александрийский, древнегреческий математик,

3 век н.э. «Арифметика» из 13 книг, 6 сохранились до наших дней.

В 5 книгах содержатся методы решения неопределенных уравнений .

Задача. В клетке сидят кролики и фазаны

вместе у них 18 ног. Узнайте сколько в клетке тех и других.

Методом перебора: (1;7), (2;5), (3;3), (4;1).

Задание №4 ОГЭ Модуль «Алгебра»

Ре­ши­те си­сте­му урав­не­ний.

В от­ве­те за­пи­ши­те сумму ре­ше­ний си­стемы.

Задание №5 ОГЭ Модуль «Алгебра»

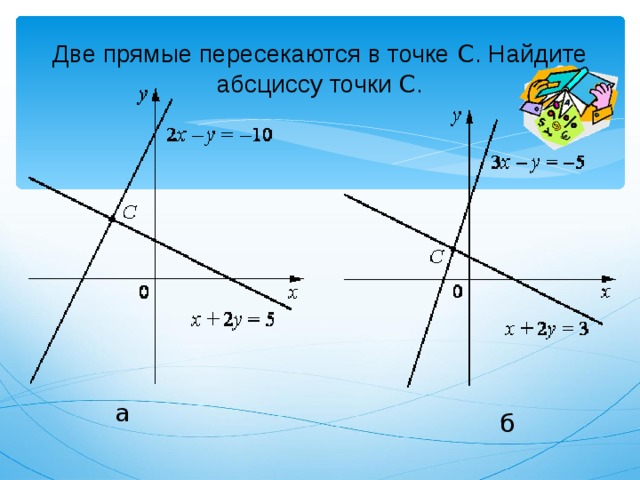
Две прямые пересекаются в точке C . Найдите абсциссу точки C .

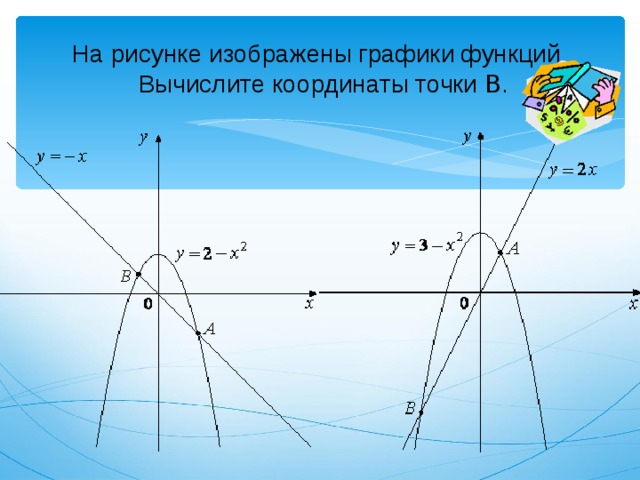
На рисунке изображены графики функций Вычислите координаты точки B .

Задание №21 ОГЭ Модуль «Алгебра»

Задание №22 ОГЭ Модуль «Алгебра»

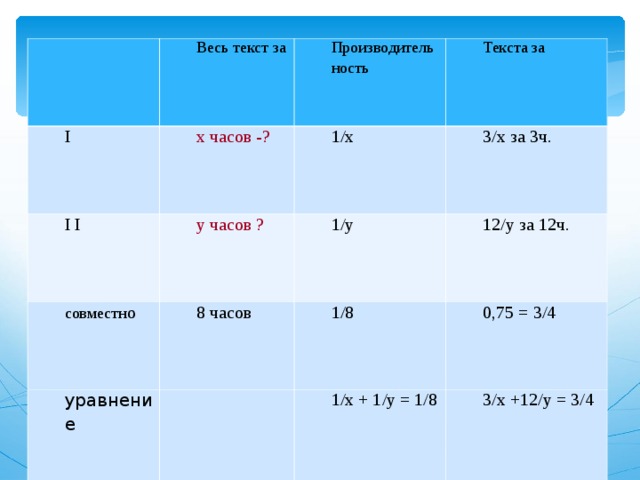
Задача на совместную работу

• Два опе­ра­то­ра, ра­бо­тая вме­сте, могут на­брать текст га­зе­ты объ­яв­ле­ний за 8 ч. Если пер­вый опе­ра­тор будет ра­бо­тать 3 ч, а вто­рой 12 ч, то они вы­пол­нят толь­ко 75% всей ра­бо­ты. За какое время может на­брать весь текст каж­дый опе­ра­тор, ра­бо­тая от­дель­но?

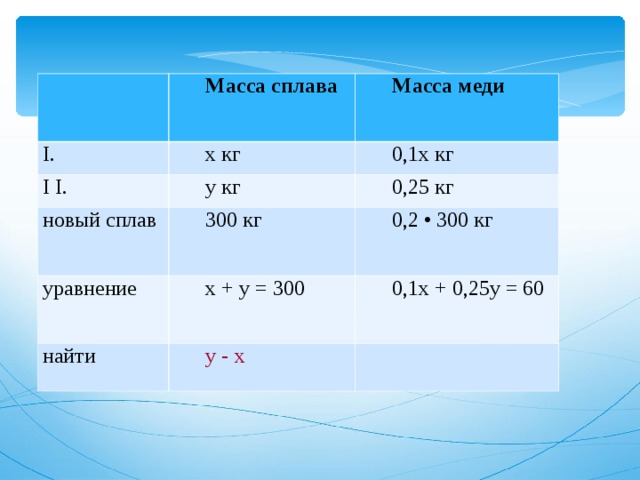
Задача на сплавы

• Первый сплав содержит 10% меди, второй — 25% меди. Их сплавили вместе и получили новый сплав массой 300 кг, содержащий 20% меди. На сколько килограммов масса первого сплава была меньше массы второго?

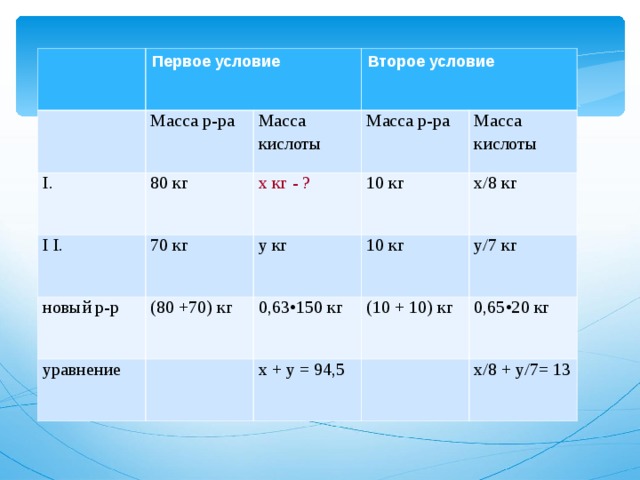
Задача на концентрацию

Имеется два сосуда. В первом 80 кг, а во втором 70 кг кислоты различной концентрации. Если смешать оба раствора, то получится 63% раствор кислоты, а если смешать равные массы этих растворов, то получится 65% раствор кислоты. Сколько килограммов кислоты содержится в первом сосуде?

• Продолжи высказывание об уроке.
• 1.На уроке для меня было важно…
• 2.На уроке мне было сложно…
• 3.Урок помог задуматься о…

Итак, сегодня мы с вами

• — Закрепили знания, умения и навыки по теме «Решение систем уравнений»
• -Познакомились с великим ученым Диофантом, его уравнениями.
• -Рассмотрели системы уравнений и задачи из банка заданий ОГЭ.

1.Задача из «Арифметики» Диофанта:

Найти два числа, зная, что их сумма равна 20, а сумма их квадратов – 208.

2. Решить системы уравнений ОГЭ:

задание 21 — № 73 , № 99 ,№ 311585

•   
•   
•   

• Решу ОГЭ. Образовательный портал для подготовки к экзаменам:

• Открытый банк заданий ОГЭ по математике:http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge

Видео:ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Уравнения. Системы уравнений. Задачи для подготовки к ОГЭ.
методическая разработка по алгебре (9 класс)

Данный сборник задач составлен в помощь учителю и ученику при подготовки к ОГЭ. Учащийся может самостоятельно изучить тему и потренироваться в решении задач, проверить ответы.

Видео:Решение систем уравнений методом подстановкиСкачать

Скачать:

Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Предварительный просмотр:

Сборник заданий для подготовки учащихся к ОГЭ. Модуль «Алгебра». Часть 2.

Уравнения. Системы уравнений.

Составитель: Глотова Е.В., учитель математики ГБОУ лицей № 373 Московского района Санкт-Петербурга «Экономический лицей».

№1. Решите уравнение .

– биквадратное уравнение. Решим его методом введения новой переменной. Пусть , тогда исходное уравнение примет вид .

Вернемся к исходной переменной:

№ 2. Решите уравнение

. Разложим левую часть уравнения на множители. Для этого вынесем общий множитель за скобки:

№ 3. Решите уравнение

. Разложим левую часть уравнения на множители методом группировки:

№ 4. Решите уравнение .

Раскроем скобки в обеих частях уравнения и упростим его:

№ 5. Решите уравнение

. Решим уравнение методом введения новой переменной.

Пусть = , тогда исходное уравнение примет вид .

Вернемся к исходной переменной:

№ 6. Решите уравнение .

№ 7. Решите уравнение

№ 8. Решите уравнение .

№ 9. Решите уравнение .

Ответ: корней нет.

№ 10. Решите уравнение .

Ответ: корней нет.

2) Выясните, имеет ли корни уравнение .

3) Сколько корней имеет уравнение .

4) Сколько корней имеет уравнение ?

5) Выясните, имеет ли действительные корни уравнение 4 .

№ 1. Решите систему уравнений

1) Приведем второе уравнение системы к целому виду, для этого умножим обе части уравнения на 6. Получим систему уравнений:

2) Выразим из первого уравнения системы переменную y и подставим во второе уравнение системы, получим уравнение

3) Подставим в уравнение , получим .

Пара решение системы.

№ 2. Решите систему уравнений

Из первого уравнения системы находим

Подставим полученное выражение во второе уравнение системы, получим:

Подставим полученные значения х в уравнение , получим:

№ 3. Решите систему уравнений

Преобразуем данную систему уравнений к виду:

Решением данной системы уравнений являются решения двух систем уравнений:

Решим каждую систему методом сложения.

Подставим полученное значение х в уравнение , получим

№ 4. Решите систему уравнений

Решением данной системы уравнений являются решения двух систем уравнений:

Решим каждую систему.

№ 5. Решите систему уравнений

Выразим из первого уравнения системы переменную x , получим .

Подставим полученное выражение во второе уравнение вместо х , получим

Умножим обе части уравнения на общий знаменатель y :

Подставим полученные значения y в выражение : .

№ 6. Вычислите координаты точек пересечения параболы и прямой .

Координаты точек пересечения параболы и прямой должны обращать оба уравнения в верные равенства, следовательно, составим и решим систему уравнений

Подставим найденные значения х во второе уравнение системы:

1. Вычислите координаты точек пересечения параболы и прямой .
2. Вычислите координаты точек пересечения парабол и .
3. Найдите точки пересечения прямой с окружностью
4. Докажите, что парабола и прямая имеют одну общую точку и найдите координаты этой точки.
5. Имеют ли графики функций и общие точки? Если имеют, то в каких координатных четвертях они находятся?

Видео:Задание №20. Экзамен ОГЭ. Система уравнений #shortsСкачать

По теме: методические разработки, презентации и конспекты

Иррациональные уравнения. Показательные уравнения.Логарифмические уравнения.

Тип урока: Урок повторения. Форма урока – мастерская (групповая работа)Форма урока работа в группах. Коллективная форма работы, которая позволяет создать ситуацию взаимообучения учащихся и сущест.

Итоговый контроль по темам № 1, 2, 3, 4: «Рациональные уравнения. Иррациональные уравнения. Квадратное уравнение и приложения теоремы Виета. Исследование квадратного трехчлена»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .

Задания на тему «Уравнения, системы уравнений»

В данном материале собраны различные задания по данной теме.

Учебный модуль по теме » Уравнение. Решение уравнений.Решение текстовых задач с помощью уравнений.»

Данный учебный модуль разработан в рамках персонализированного обучения .Модуль расчитан на 12 часов. Содержитз адания для прохождения уровней цели 2.0,,3.0 и 4.0.В модуле представле.

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Уравнения,системы уравнений. Подготовка к ОГЭ

Подготовка к ОГЭ. Уравнения, системы уравнений.

Задачник с ответами для подготовки к ОГЭ по математике ( задание № 9 , уравнения и системы уравнений)

Данная система заданий позволяет отработать навыки по решению задания № 9 ОГЭ по математике. Для проверки в конце сборника публикуются ответы.

💡 Видео

9 класс, 11 урок, Методы решения систем уравненийСкачать

Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Задание 21. Уравнения и системы уравнений. Подготовка к ОГЭ 2020. Вебинар | МатематикаСкачать

Неравенства. 2 правила для решения | Математика ОГЭ 2022 | УмскулСкачать

ОГЭ Задание 20 Разные способы решения систем уравненийСкачать

ОГЭ по математике 2022. Уравнения. Системы уравнений.Скачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать