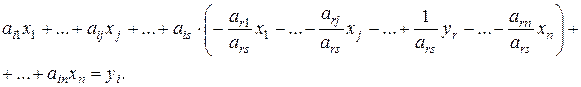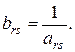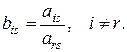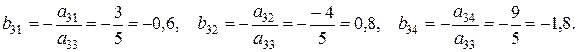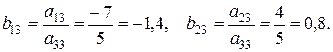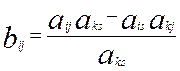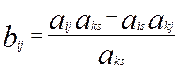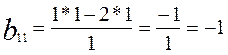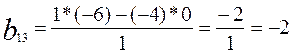Данный онлайн калькулятор находит общее решение системы линейных уравнений методом Жордана-Гаусса. Дается подробное решение. Для вычисления выбирайте количество уравнений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.» Теоретическую часть нахождения решения системы линейных уравнений методом Жордана-Гаусса смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Разбор метода жордановых исключений. Алгебра и геометрия.Скачать

Метод Жордана-Гаусса
Метод Жордана-Гаусса − это метод для решения систем линейных уравнений а также метод нахождения обратной матрицы. Данный метод является модификацией метода Гаусса.
Первый этап метода Жордана-Гаусса аналогична методу Гаусса (прямой ход Гаусса), который подробно можно посмотреть на странице «Метод Гаусса онлайн». Второй этап (обратный ход) метода Жордана-Гаусса заключается в обнулении всех элементов матрицы коэффициентов системы линейных уравнений, выше ведущих элементов. Отметим, что мы здесь рассматриваем произвольную систему линейных уравнений, где число переменных может быть не равным числу ограничений.
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Запишем систему (1) в матричном виде:
| Ax=b | (2) |
  | (3) |
A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.
Построим расшренную матрицу системы:
 | (4) |
После прямого хода Гаусса (подробнее о прямом ходе Гаусса посмотрите на странице «Метод Гаусса онлайн») получим следующую расширенную матрицу:
 | (5) |
Если 

Пусть 

Итак, обнуляем все элементы, стоящие в столбце p, выше элемента 


Расширенная матрица примет следующий вид:
 |
Аналогичным методом обнуляем элементы столбцов p−1, p−2, . 2 выше ведущих элементов 
Расширенная матрица примет следующий вид:
 |
Делим каждую строку на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Тогда решение можно записать так:
 |
где 
Отметим, что при m=n и rangA=n система линейных уравнений (2) имеет единственное решение.
Рассмотрим численные примеры.
Видео:Решение системы уравнений методом ГауссаСкачать

Примеры решения системы линейных уравнений методом Жордана-Гаусса
Пример 1. Найти решение системы линейных уравнений методом Жордана-Гаусса:
 |
Матричный вид записи: Ax=b, где
 . . |
Для решения системы, построим расширенную матрицу:
 . . |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на 1/2,-3/2 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 1/5:
 . . |
Второй этап. Обратный ход Гаусса
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строки 1, 2 со строкой 3, умноженной на -3/2, -5/4 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на -2/5:
 . . |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . . |
 . . |
Векторный вариант решения:
 . . |
Пример 2. Найти решение системы линейных уравнений методом Жордана-Гаусса:
 |
Матричный вид записи: Ax=b, где
 |
Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на 4/3, 5/3 соответственно:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на -2:
 |
Второй этап. Обратный ход Гаусса
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на -3/10:
 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Выразим переменные x1, x2 относительно остальных переменных.
 |
x3− произвольное действительное число.
Векторный вариант решения:
Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:
 |
Тогда векторное решение можно представить так:
 , , |
x3− произвольное действительное число.
Видео:Метод Жордана-Гаусса (метод прямоугольников). ВидеоурокСкачать

Метод обыкновенных жордановых исключений
ПРИЛОЖЕНИЯ
Наиболее простым методом преобразования систем линейных уравнений традиционно считается метод Гаусса-Жордана. При помощи данного метода можно найти единственное решение системы линейных уравнений или доказать его отсутствие. А в том случае, когда система имеет бесчисленное множество решений, метод Гаусса-Жордана позволяет находить базисные решения системы и переходить всего за один шаг от одного базисного решения к другому. Такая особенность метода Гаусса-Жордана позволила на его основе реализовать так называемый симплекс-метод решения задач линейного программирования.
Однако существует еще один метод преобразования систем линейных уравнений – метод жордановых исключений. По существу, это хорошо всем нам знакомый метод исключения неизвестных. Однако практическая реализация данного метода в виде жордановых таблиц позволила существенно сократить арифметические вычисления. Это заметно даже при решении задач линейной алгебры. Но особенно это заметно во время решения задач математического программирования. Применительно к задачам линейного программирования, метод жордановых исключений получил название метода Штифеля.
Метод Штифеля успешно применяется в математическом программировании не только потому, что он существенно проще традиционного симплекс-метода. Самое главное его достоинство заключается в том, что он позволяет примерно вдвое сократить количество учебных часов, необходимых преподавателю для прочтения курса линейного программирования.
Пособие состоит из четырех частей. В первой части изучаются методы жордановых исключений и модифицированных жордановых исключений. Данные методы преобразования систем линейных равенств оформляются в виде жордановых таблиц. Приведены и доказаны алгоритмы перехода от одной жордановой таблицы к другой (один шаг жордановых исключений).
Во второй главе изучаются применение метода жордановых исключений в линейной алгебре. Применение метода жордановых исключения к решению стандартных задач линейной алгебры оказалось вполне оправданным. На примерах доказано, что решение таких задач, как вычисление ранга матрицы, нахождение обратной матрицы и решение систем линейных уравнений методом жордановых исключений оказалось проще, чем решение традиционными методами.
В третьей и четвертой главе данного пособия содержится краткое изложение курса математического программирования, основанного на методе жордановых исключений (метод Штифеля).
Пособие, прежде всего, предназначено для студентов математических факультетов, получающих специальность «Преподаватель». Данное пособие также полезно студентам экономических и других специальностей, изучающих математическое программирование и линейную алгебру.
МЕТОД ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ
Метод обыкновенных жордановых исключений
Пусть дана система линейных форм (уравнений):
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного
(r -го) равенства выразим произвольную переменную (xs) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда ars ¹ 0. Коэффициент ars называется разрешающим (иногда направляющим или главным) элементом. Мы получим следующую систему:
Вычислим коэффициенты полученной системы (1.2) через коэффициенты исходной системы (1.1). Начнем с r-го уравнения, которое после выражения переменной xs через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r-го уравнения вычисляются по следующим формулам:

Вычислим теперь новые коэффициенты bij (i ¹ r) произвольного уравнения. Для этого подставим выраженную в (1.3) переменную xs в
i-е уравнение системы (1.1):
После приведения подобных членов, получим:

Из равенства (1.5) получим формулы, по которым вычисляются остальные коэффициенты системы (1.2) (за исключением r-го уравнения):

Как и в случае решения линейных уравнений, методом Гаусса, преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых». Так, задаче (1.1) ставится в соответствие следующая жорданова таблица:
| x1 | x2 | … | xj | … | xs | … | xn |
| y1 | a11 | a12 | a1j | a1s | a1n | ||
| ………………………………………………………………….. | |||||||
| yi | ai1 | ai2 | aij | ais | ain | ||
| ………………………………………………………………….. | |||||||
| yr | ar1 | ar2 | arj | ars | arn | ||
| …………………………………………………………………. | |||||||
| yn | am1 | am2 | amj | ams | amn |
Системе (1.2) при этом соответствует жорданова таблица:
| x1 | x2 | … | xj | … | yr | … | xn |
| y1 | b11 | b12 | b1j | b1s | b1n | ||
| ………………………………………………………………….. | |||||||
| yi | bi1 | bi2 | bij | bis | bin | ||
| ………………………………………………………………….. | |||||||
| xs | br1 | br2 | brj | brs | brn | ||
| …………………………………………………………………. | |||||||
| yn | bm1 | bm2 | bmj | bms | bmn |
Разрешающий элемент ars мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений соответствующий разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. Независимые переменные x1, x2,…, xn записывают в верхней заглавной строке таблицы. Зависимые переменные y1, y2,…, yn – в левом заглавном столбце. При переходе от данной таблицы к следующей одна переменная из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, одна переменная из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку. То есть меняются местами переменные, содержащиеся в разрешающем столбце и разрешающей строке.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.4) и (1.6).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь 
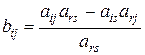
| aij | ais |
| + | – |
| arj | ars |
Пример 1.1. Пусть дана система равенств:
Данную систему можно записать в виде следующей жордановой таблицы:
| x1 | x2 | x3 | x4 |
| y1 | -7 | ||
| y2 | -6 | ||
| y3 | -4 |
Выберем в качестве разрешающего элемента число 5, находящееся на пересечении 3-ей строки и 3-го столбца. При этом переменная x3 меняется с переменной y3 местами, и мы получим новую таблицу:
| x1 | x2 | y3 | x4 | |
| y1 | 8,2 | -3,6 | -1,4 | 18,6 |
| y2 | 5,6 | 8,2 | 0,8 | -13,2 |
| x3 | -0,6 | 0,8 | 0,2 | -1,8 |
Подробно поясним, как были получены коэффициенты новой системы.
1. Разрешающий элемент заменился на обратное число:
2. Остальные элементы разрешающей строки вычислялись по формуле:
3. Остальные элементы разрешающего столбца вычислялись по формуле:
4. Остальные коэффициенты системы пересчитывались по формулам:
Видео:6 способов в одном видеоСкачать

Решение систем линейных уравнений с помощью жордановых исключений
Решение систем линейных уравнений с помощью жордановых исключений
Модифицированные жордановы исключения
Часто пользуются модифицированными жордановыми исключениями. В этом случае жордановы таблицы отличаются тем, что в них
v переменные в заглавной строке записываются со знаком минус (независимые переменные),
v i-й шаг жорданова исключения переводит эту исходную таблицу в любую по правилу:
— разрешающий элемент заменяется обратной величиной
— остальные элементы разрешающей строки делятся на разрешающий элемент
— остальные элемента разрешающего столбца делятся на разрешающий элемент и меняют знаки
— прочие элементы вычисляются по формуле
После каждого шага жордановых исключений вычеркивается разрешающий столбец и строки, содержащие целиком нулевые элементы.
Пример 1. Решить систему, пользуясь модифицированными жордановыми исключениями. Не забывать пересчитать свободные члены.
|
Решение
1. Запишем СЛАУ в форме жордановой таблицы
| — х1 | -х2 | -х3 | — х4 |
| -3 | — 6 | ||
| — 4 | |||
| — 2 |
2. Проделать возможное число модифицированных жордановых исключений
ü Ввести в базис, например, — х2
| — х1 |  -х2 -х2 | -х3 | — х4 |
| -3 | — 6 | ||
 0 0 | 0 | — 4 | |
| 3 | — 2 |
| -х1 | -х3 | — х4 |
| х2 |
|
ü Используя данные исходной таблицы пересчитать элементы разрешающей строки и разрешающего столбца, по правилу:
— разрешающий элемент заменить обратной величиной
— остальные элементы разрешающей строки разделить на разрешающий элемент
— остальные элементы разрешающего столбца разделить на разрешающий элемент и поменять знаки
ü пересчитать остальные элементы таблицы по правилу
| -х1 | -х3 | — х4 |
| bij | -2 | |
| х2 | — 4 |
 |
 |
|
|
| -х1 | -х3 | — х4 |
| -3 |   1 1 | — 6 |
| х2 | 0 | — 4 |
| 3 | — 2 |
| -х1 | -х3 | — х4 |
| -1 | -2 | |
| х2 | 0 | — 4 |
| -х1 | -х3 | — х4 |
| -3 |   2 2 | — 6 |
| х2 | 0 | — 4 |
| 3 | — 2 |
| -х1 | -х3 | — х4 |
| -1 | -2 | -2 |
| х2 | 0 | — 4 |
В результате получим следующую таблицу
| -х1 | -х3 | — х4 | |
| -3 | -1 | -2 | -1 |
| х2 | 0 | — 4 | |
| 3 | — 2 |
ü Из нее вычеркиваем столбец с 0 в заглавной строке
 -х1 -х1 | -х3 | — х4 |
| -3 | -1 | -1 |
| х2 | 0 | — 4 |
 0 0 | 3 | — 2 |
ü В этой таблице введем в базис х1
| -х3 | — х4 | |
| -3 | -1 | -1 |
| х2 | 0 | — 4 |
| х1 | 3 | — 2 |
ü Пересчитаем опять всю таблицу
| -х3 | — х4 | |
| х2 | -3 | — 2 |
| х1 | — 2 |
| -х3 | — х4 | ||
| х2 | -3 | -1 | — 2 |
| х1 | 3 | — 2 |
ü Получили решение:
х3 и х4 могут принимать любые значения свободные переменные
💡 Видео
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение системы уравнений методом Гаусса 4x4Скачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем уравнений методом сложенияСкачать

решение системы уравнений методом ГауссаСкачать

Метод Гаусса и метод Жордана-ГауссаСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Решаем систему методом подстановки. ЕГЭ-2023 по математике.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать