Решение систем уравнений методом главных элементов (2 видео)

Метод главных элементов.

Сумы 2006

Содержание

Постановка задачи

2. Точные методы решения СЛАУ

3. Практическая реализация метода Халецкого

3.1 Программа на языке Pascal

3.2 Решение в Excel

Решить систему линейных алгебраических уравнений, используя точный метод численного решения (схему Халецкого).

Введение

Существует несколько способов решения таких систем, которые в основном делятся на два типа: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы, 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов.

Для того чтобы система линейных алгебраических уравнений имела решение, необходимо и достаточно, чтобы ранг основной матрицы был равен рангу расширенной матрицы. Если ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных, то система имеет единственное решение. Если ранг основной матрицы равен рангу расширенной матрицы, но меньший числа неизвестных, то система имеет бесконечно решений.

Пример системы линейных уравнений:

Или в матричном виде: ,

где матрица коэффициентов системы;

— вектор неизвестных; — вектор свободных членов.

Точные методы решения СЛАУ

Метод главных элементов.

Пусть дана система линейных алгебраических уравнений. Рассмотрим расширенную матрицу, состоящую из коэффициентов системы a[i,j] и свободных членов b[i]. Метод главных элементов — это обобщение метода исключения переменных (метода Гаусса). Обозначим матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов исходной системы за M.

Выбираем наибольший по модулю элемент, не принадлежащий столбцу свободных членов. Пусть это будет 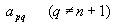. Этот элемент называется главным элементом, а строка, в которой он находится, называется главной строкой.

Далее производим следующие преобразования: к каждой неглавной строке прибавим главную строку, умноженную на соответствующий множитель для этой строки. В результате мы получим матрицу, у которой q-й столбец состоит из нулей. Отбросим этот столбец и главную p-ю строку, получим новую матрицу с меньшим на единицу числом строк и столбцов. Над матрицей повторяем те же операции, после чего получаем матрицу и т.д. Таким образом, мы построим последовательность матриц

последняя, из которых представляет двучленную матрицу — строку, её также будем считать главной строкой. Для определения неизвестных объединяем в систему все главные строки, начиная с последней. После надлежащего изменения нумерации неизвестных получается система с треугольной матрицей, из которой легко шаг за шагом найти неизвестные данной системы.

Заметим, что метод Гаусса является частным случаем, метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. Запрограммировать метод главных элементов непросто, поэтому чтобы уменьшить вычислительную погрешность, применяют метод Гаусса с выбором главного элемента. Необходимое условие применения метода главных элементов: определитель системы не равен нулю.

Содержание

Метод Гаусса с выбором главного элемента
Решение задач по математике онлайн
Калькулятор онлайн. Решение систем линейных алгебраических уравнений (СЛАУ) Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Формы записи СЛАУ
Критерий совместности СЛАУ
Формулы Крамера
Однородные системы
Неоднородные системы
🌟 Видео

Видео:Матричный метод решения систем уравненийСкачать

Метод Гаусса с выбором главного элемента

Московский Государственный Технически Университет

«МАМИ»

Лабораторная работа №3 по курсу «Вычислительная Математика»

«РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ»

3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Справочная информация

Численные методы решения систем линейных алгебраических уравнений

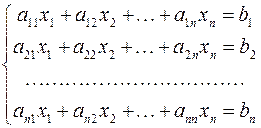
записываемых в матричной форме в виде

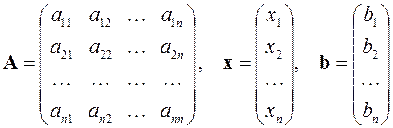
делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A — не вырождена (её определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости.

Точные методы, к которым относятся метод Гауссаи его разновидности, не имеют дополнительных ограничений на свойства матрицы системы.

В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей

Данное преобразование может быть осуществлено многими способами. Однако все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением.

Один из простейших способов исключения состоит в следующем. Первое уравнение системы

которое на этом шаге считается ведущим, нормируется – делится на значение диагонального элемента a₁₁

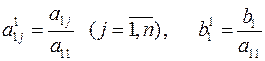
Если в исходной системе a₁₁= 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a₂₁ и вычитается из него. В результате во втором уравнении пропадает слагаемое a₂₁x₁, содержащее первое неизвестное x₁. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид

Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x₂ из всех уравнений, начиная с третьего

Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования:

Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение x_n, что позволяет определить x_n_–1 из предпоследнего уравнения как

Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения x_n_–2. x₂, x₁.

Метод Гаусса даёт точное решение, если все исходные данные точны и все вычисления производятся точно. На практике, при выполнении вычислений, неизбежно проводятся округления. Ошибка округлений вносит погрешность в решение метода Гаусса. Таким образом, при операциях с округленными десятичными числами метод Гаусса даёт не точное решение x_т системы линейных алгебраических уравнений, а некоторое приближённое решение , где

, .

Степень отличия приближённого решения от точного определяется длиной разрядной сетки ЭВМ: чем больше разрядов в ней учитывается, тем это отличие меньше.

При определении погрешности вектора решения необходимо учитывать, что его компоненты в общем случае могут иметь разную погрешность. В силу этого погрешность решения принято оценивать по его норме

или или

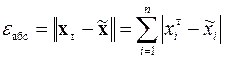
где двойные модульные скобки обозначают норму вектора.

Для определения величины погрешности полученного решения на практике используют следующий алгоритм вычисления её главной части. Сначала по имеющемуся решению пересчитывается вектор правых частей системы

а затем посредством повторного решения системы уравнений

находится вектор погрешностей . С его помощью определяется как реальная абсолютная погрешность полученного решения

или или ,

так и его относительная погрешность

Величина погрешности решения системы уравнений, получаемого методом Гаусса, зависит от двух основных факторов. Первый из них, как это было сказано выше – длина разрядной сетки, используемой в процессе вычислений, а второй – обусловленность матрицы системы. Обусловленность матрицы можно рассматривать как степень её чувствительности к накоплению ошибок округления в процессе преобразований. Снижение величины погрешности решения может быть достигнуто увеличением длины разрядной сетки. Повлиять на величину погрешности посредством изменения степени обусловленности матрицы системы невозможно, так как она является одной из её характеристик и изменение степени обусловленности матрицы требует изменения самой матрицы.

Метод Гаусса с выбором главного элемента

Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего уравнения. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используетсяуравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца, i-ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй – по строке, а третий – по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения.

В качестве примера применения метода Гаусса можно рассмотреть задачу отыскания решения следующей системы уравнений

при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения.

Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.

а. Выбор главного элемента среди элементов первого столбца

б. Нормировка первого уравнения

в. Исключение элементов первого столбца

г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений

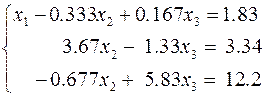
д. Нормировка второго уравнения

е. Исключение элементов второго столбца

ё. Нормировка последнего уравнения

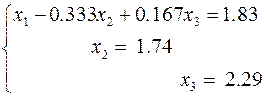
В итоге получено решение системы уравнений

3. Погрешность найденного решения.

а. Пересчёт вектора правых частей системы

б. Формирование системы уравнений, определяющей погрешности решения

в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей

а обратный ход позволяет получить решение

г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений

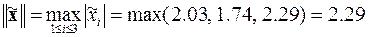
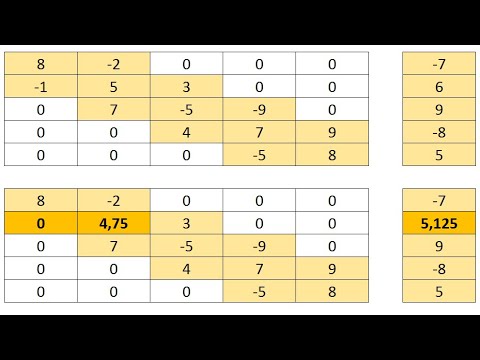
Реализация описанного метода без нахождения погрешности решения в рамках программы Excel приведена на рис.1.

О выборе метода решения систем уравнений

Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Для этого требуется выполнить n(n 2 + 3n – 1)/3 операций умножения и деления и n(n – 1)(2n + 5)/6 операций сложения и вычитания, количество которых при больших порядках системы (n > 100) можно принять равным n 3 /3 в обоих случаях. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов.

Итерационные методы позволяют получать решение систем бóльшего порядка. Для выполнения каждой итерации с их помощью необходимо выполнить n(n + 1) операций умножения и деления и столько же операций сложения и вычитания. При больших порядках системы уравнений (n > 100) их количество можно принять равным n 2 . Из сравнения трудоёмкости итерационных методов и метода Гаусса следует оценка, которой можно руководствоваться при окончательном выборе метода решения системы при необходимости его многократного нахождения. Если количество итераций, требуемое для получения решения системы итерационными методами, не превышает n/3, то выгоднее применять их, а не методы типа Гаусса. Однако здесь следует помнить, что итерационные методы требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости их сходимости.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Решение системы уравнений методом ГауссаСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )

Ввод: -1,15
Результат: ( -115 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Видео:Решение системы уравнений методом Крамера.Скачать

Немного теории.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.