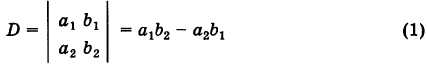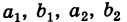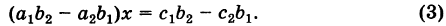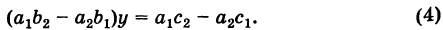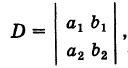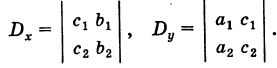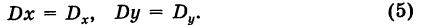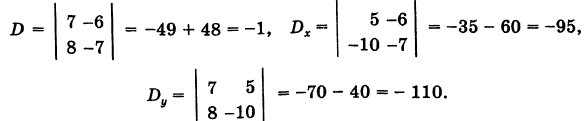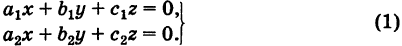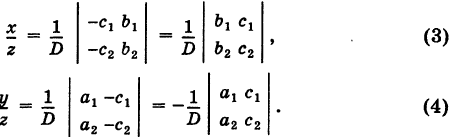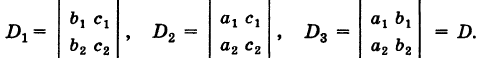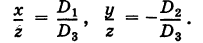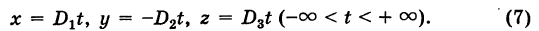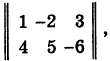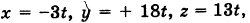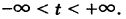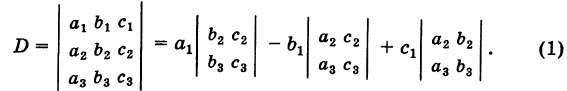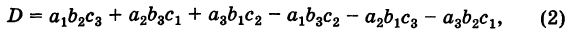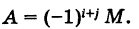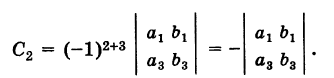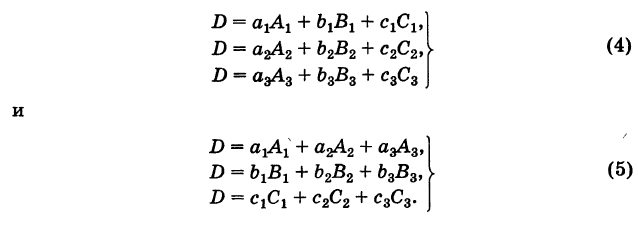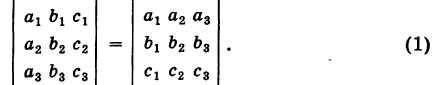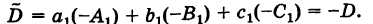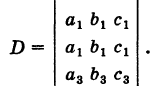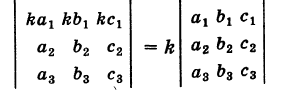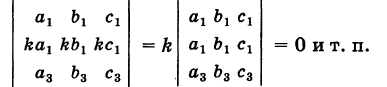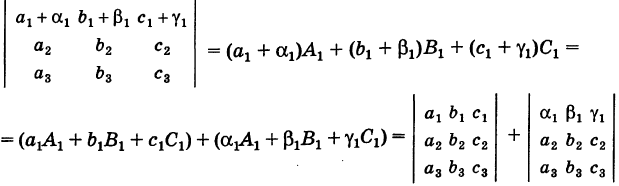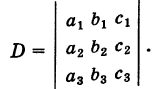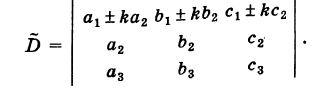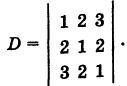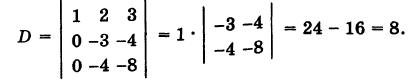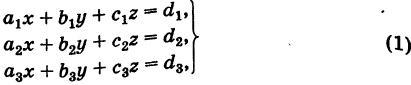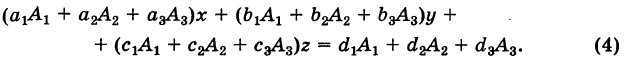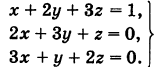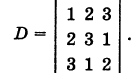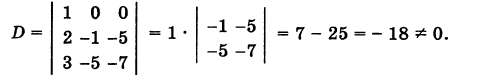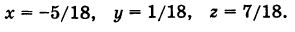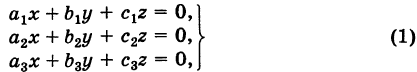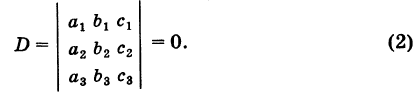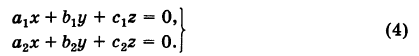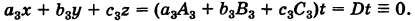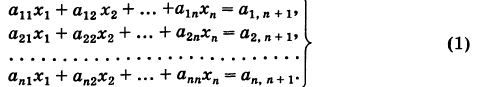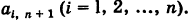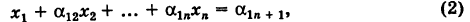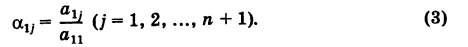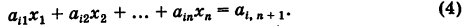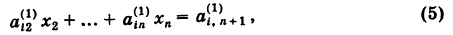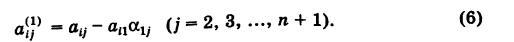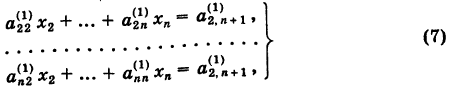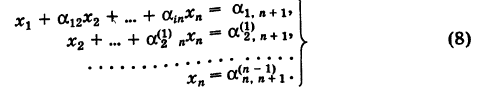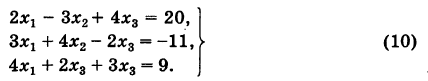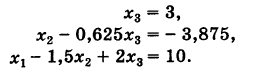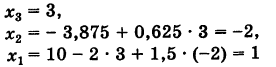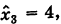Решение систем уравнений 3 го порядка (8 видео)

Определители второго и третьего порядков и их свойства с примерами решения

Содержание:

Определители второго порядка:

Под определителем (детерминантом) второго порядка понимается выражение

Числа

Формула (1) дает правило «развертывания» определителя второго порядка, а именно: определитель второго порядка равен разности произведений его элементов первой и второй диагоналей.

Содержание

Определители второго порядка
Система двух однородных уравнений с тремя неизвестными
Определители третьего порядка
Основные свойства определителей
Система трех линейных уравнений
Однородная система трех линейных уравнений
Система линейных уравнений с многими неизвестными. Метод Гаусса
Решение СЛАУ 3-его порядка методом Гаусса, пример № 11
Решение систем уравнений 3 го порядка
Контакты
📸 Видео

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Определители второго порядка

С помощью определителей второго порядка удобно решать линейные системы двух уравнений с двумя неизвестными:

Такую линейную систему, в которой свободные члены находятся в правых частях, для определенности мы будем называть стандартной.

Под решением системы (2) понимается всякая пара чисел (х, у), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным. Аналогично вводится понятие решения для системы, содержащей п неизвестных .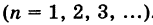

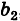
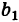
Для нахождения решений системы (2) применим метод исключения. Умножая первое уравнение системы (2) на , а второе — на — и складывая, будем иметь

Аналогично, умножая первое уравнение системы (2) на а₂ второе — на 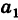складывая, получаем

Введем определитель системы

а также дополнительные определители

Заметим, что дополнительные определители Dx и Dy получаются из определителя системы D путем замены коэффициентов при указанном неизвестном на соответствующие свободные члены.

Уравнения (3) и (4) принимают вид

Если 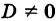, то отсюда получаем, что система (2) имеет единственное решение

Замечание. Если определитель D = 0, то система (2) или не имеет решений (т. е. несовместна), или имеет бесконечно много решений (т. е. система неопределенная).

Пример:

Решение:

Имеем

Отсюда на основании формул Крамера (6) получаем

Геометрически решение (95; 110) представляет собой точку пересечения прямых (7).

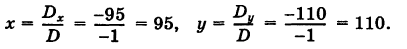
Видео:Решение системы уравнений методом ГауссаСкачать

Система двух однородных уравнений с тремя неизвестными

Рассмотрим однородную систему

Эта система всегда совместна, так как, очевидно, имеет нулевое решение х = 0, у = 0, z = 0. Однако интересно найти не н у л е в ы е решения (х, у, z) системы (1). Пусть, например, .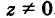

Тогда систему (1) можно переписать в виде

Отсюда, предполагая, что , получаем

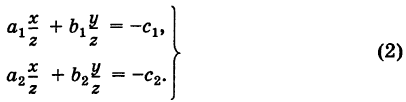
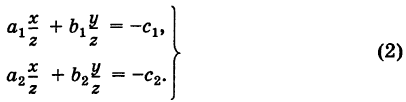
Введем в рассмотрение матрицу коэффициентов системы (1)

Определители второго порядка 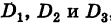, которые получаются из матрицы (5) путем вычеркивания соответствующего столбца, называются ее минорами. Таким образом, имеем

Используя эти обозначения, уравнения (3) и (4) можно переписать в следующем виде:

Равенства (6), очевидно, справедливы также и для нулевого решения.

Таким образом, имеем следующее правило: неизвестные однородной системы (1) пропорциональны соответствующим минорам ее матрицы коэффициентов, взятым с надлежащими знаками.

Обозначая через t коэффициент пропорциональности для отношений (6), получим полную систему решений системы (1):

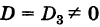
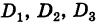
При выводе формул (7) мы предполагали, что . Однако, как легко убедиться, формулы (7) будут справедливы, если любой (хотя бы один) из миноров отличен от нуля.

Замечание. Если все миноры 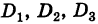равны нулю, то система (1) требует особого рассмотрения.

Пример:

Решение:

Составляя матрицу коэффициентов

находим ее миноры: 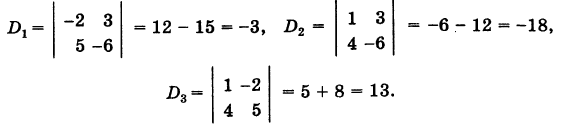На основании формулы (7) полная система решений системы (8) имеет вид

где

Простейшее ненулевое решение системы (1), получающееся при t — 1, есть х = -3, у = 18, z = 13.

Видео:Матричный метод решения систем уравненийСкачать

Определители третьего порядка

Числа 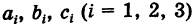называются элементами определителя; они расположены в трех строках и трех столбцах его (ряды определителя). ,

Раскрывая определители второго порядка (миноры) в формуле (1) и собирая члены с одинаковыми знаками, получаем, что определитель третьего порядка представляет собой знакопеременную сумму шести слагаемых:

из которых три берутся со знаком плюс, а три — со знаком минус.

Пример:

Решение:

Используя формулу (1), имеем В дальнейшем мы укажем более удобные способы вычисления определителей третьего порядка.

Определение: Под минором элемента определителя третьего порядка понимается определитель младшего (второго) порядка, получающийся из данного определителя в результате вычеркивания строки и столбца, содержащих данный элемент.

Например, для определителя (3) минором его элемента 2, стоящего во второй строке и в первом столбце, является определитель 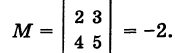В дальнейшем для краткости будем говорить, что элемент определителя третьего порядка занимает четное место, если сумма номеров его строки и его столбца есть число четное, и нечетное место, если эта сумма есть число нечетное.

Определение: Алгебраическим дополнением (минором со знаком) элемента определителя третьего порядка называется минор этого элемента, взятый со знаком плюс, если элемент занимает четное место у и со знаком минус, если его место нечетное.

Таким образом, если М есть минор элемента определителя, a i и j — соответственно номер строки и номер столбца, на пересечении которых находится данный элемент, то его алгебраическое дополнение есть

Например, для элемента с₂ определителя (1), находящегося во второй строке и в третьем столбце, его алгебраическое дополнение есть

Соответствующие знаки, приписываемые при этом минорам элементов определителя, можно задать таблицей

В дальнейшем алгебраические дополнения элементов определителя с буквенными элементами условимся обозначать соответствующими прописными (большими) буквами.

Теорема Разложения: Определитель третьего порядка равен сумме парных произведений элементов какого-либо ряда его на их алгебраические дополнения (под рядом понимается строка или столбец).

Таким образом, для определителя (1) справедливы шесть разложений:

Легко проверить, что формулы (4) и (5) дают одно и то же выражение (2), принятое за определение.

Замечание. С помощью формул типа (4) или (5), по индукции, можно ввести определители высших порядков.

Видео:Система с тремя переменнымиСкачать

Основные свойства определителей

При формулировках мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка.

I. (Равноправность строк и столбцов.) Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, т. е.

Действительно, разлагая первый определитель по элементам первой строки, а второй — по элементам первого столбца, в силу теоремы разложения мы получим один и тот же результат.

II. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на обратный.

Пусть, например, в определителе переставлены первая и вторая строки; тогда получим определитель Разлагая определитель D по элементам второй строки и учитывая, что при перестановке строк изменилась четность мест этих элементов, будем иметь

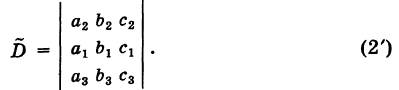
Аналогичное положение получается и в других случаях.

Следствие 1. Определитель, у которого два параллельных ряда одинаковы, равен нулю.

В самом деле, пусть, например,

Переставляя первую и вторую строки определителя, в силу теоремы получим определитель -D. Но очевидно, эта операция не изменяет определитель D, поэтому -D = D и, следовательно, D = 0.

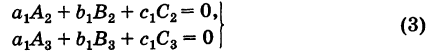
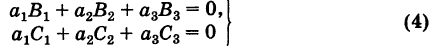
Следствие 2. Сумма парных произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю, т. е. для определителя (2) имеем и т. д., а также и т. д. (всего таких соотношений можно написать двенадцать).

Левые части всех соотношений (3) и (4) представляют собой разложения соответствующих определителей третьего порядка, содержащих два одинаковых параллельных ряда и, следовательно, равны нулю. Например, 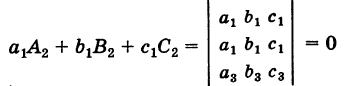(здесь разложение нужно производить во второй строке!).

III. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя, т. е.

Это свойство непосредственно вытекает из разложения определителя по элементам соответствующего ряда.

Следствие 1. Если все элементы какого-либо ряда определителя равны нулю, то определитель равен нулю.

Следствие 2. Если элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда его, то определитель равен нулю.

Например, имеем

IV. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Следствие. Величина определителя не изменится, если /с элементам какого-либо ряда его прибавить (или отнять) числа, пропорциональные соответствующим элементам параллельного ряда с одним и тем же коэффициентом пропорциональности (так называемые «элементарные преобразования определителя»).

Рассмотрим, например, определители

Используя свойства IV и III, будем иметь 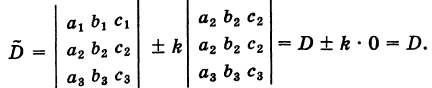Элементарные преобразования дают удобный способ вычисления определителей.

Пример:

Вычислить симметричный определитель

Решение:

Вычитая из второй строки удвоенную первую строку, а из третьей строки утроенную первую строку, получим

Система трех линейных уравнений

Рассмотрим стандартную линейную систему трех уравнений

свободные члены которых находятся в правых частях. Под решением системы понимается всякая тройка чисел (х, у, г), удовлетворяющая этой системе. Введем определитель системы

а также дополнительные определители

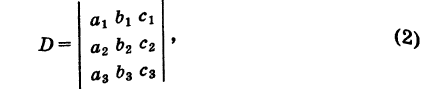
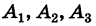
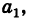
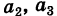
Последовательно умножая уравнения системы (1) на алгебраические дополнения соответствующих элементов первого столбца определителя D, получим

Отсюда, применяя теорему разложения и следствие 2 к свойству II, будем иметь 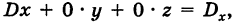, т. е. Используя алгебраические дополнения элементов второго и третьего столбцов определителя D, аналогично находим

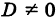
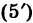
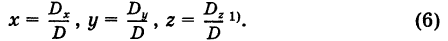
Если определитель системы , то из уравнений (5) и получаем единственное решение системы (1): Таким образом, имеем правило Крамера: неизвестные стандартной линейной системы (1) с ненулевым определителем представляют собой дроби, знаменатель которых есть определитель системы, а числители равны соответствующим дополнительным определителям.

Замечание. Если определитель системы D = 0, то система (1) или несовместна, или имеет бесконечно много решений.

Пример:

Решение:

Вычитая из второго столбца удвоенный первый столбец, а из третьего столбца утроенный первый столбец, получим

Для дополнительных определителей находим следующие значения: 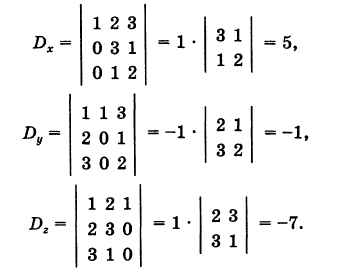Используя правило Крамера, получаем решение системы:

Однородная система трех линейных уравнений

Рассмотрим линейную систему

свободные члены которой равны нулю. Такая линейная система называется однородной.

Однородная линейная система (1), очевидно, допускает нулевое решение х = 0, у = 0, z = 0 и, следовательно, всегда совместна.

Интересно выяснить случаи, когда однородная система имеет ненулевые решения.

Теорема: Линейная однородная система трех линейных уравнений с тремя неизвестными имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т. е.

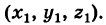
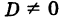
Доказательство: Пусть система (1) имеет ненулевое решение Если определитель ее то на основании формул Крамера система (1) обладает только нулевым решением, что противоречит предположению. Следовательно, D = 0.

Пусть D = 0. Тогда линейная система (1) либо несовместна, либо имеет бесконечно много решений. Но наша система совместна, так как имеется нулевое решение. Следовательно, система (1) допускает бесконечно много решений, в том числе и ненулевые.

Замечание. Укажем способ нахождения ненулевых решений однородной системы (1) в типичном случае.

Пусть определитель системы D = 0, но не все его миноры второго порядка равны нулю.

Мы будем предполагать, что

(этого всегда можно добиться с помощью перестановки уравнений и изменения нумерации неизвестных).

Рассмотрим подсистему, состоящую из двух первых уравнений системы (1):

В силу решения этой системы имеют вид

где — соответствующие алгебраические дополнения. Подставляя эти числа в неиспользованное третье уравнение системы (1) и учитывая, что определитель D = 0, получаем

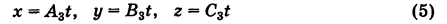
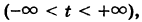
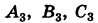
Следовательно, формулы (5), где t произвольно, дают все решения полной системы (1).

Геометрически уравнения системы (1) представляют собой уравнения трех плоскостей в пространстве Oxyz. Если определитель 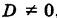, то эти плоскости пересекаются в единственной точке 0(0, 0, 0); если же определитель D =0, но не все его миноры второго порядка равны нулю, то в нашем случае эти плоскости пересекаются по прямой линии (как «листы книги»). Без рассмотрения оставлен случай слияния трех плоскостей.

Система линейных уравнений с многими неизвестными. Метод Гаусса

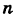
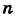
Рассмотрим систему линейных уравнений с неизвестными:

Здесь для коэффициентов системы введена двойная индексация, а именно: у коэффициента 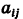первый индекс i обозначает номер уравнения, а второй j — номер неизвестного. Для удобства выкладок свободные члены обозначены через

Наиболее простой метод решения системы (1) — это метод исключения. Мы изложим его в форме схемы Гаусса (обычно называемой методом Гаусса).

Пусть для определенности 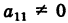— ведущий коэффициент». Разделив все члены первого уравнения на аи, будем иметь приведенное уравнение

Рассмотрим i-e уравнение системы (1):

Для исключения xx из этого уравнения умножим приведенное уравнение (2) на ап и полученное уравнение вычтем из уравнения (4). Тогда будем иметь

Таким образом, получаем укороченную систему

коэффициенты которой определяются по формулам (6).

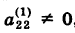
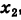
Если ее ведущий коэффициент , то из системы (7) указанным выше приемом можно исключить неизвестное . причем новые коэффициенты будут вычисляться по формулам типа (6) и т.д. Эта часть вычислений называется прямым ходом метода Гаусса.

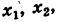
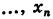
Для определения неизвестных Рассмотрим приведенные уравнения

Отсюда последовательно находим неизвестные (обратный ход) 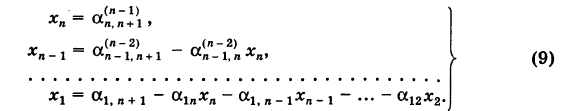Заметим, что операции (9) выполняются без деления.

Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.

Пример:

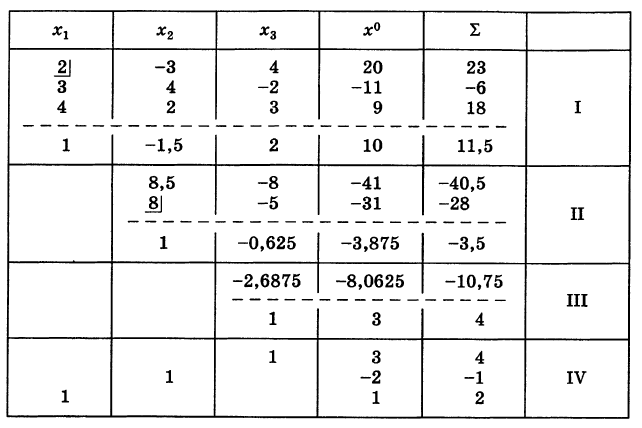
Методом Гаусса решить систему

Решение:

Составляем таблицу коэффициентов системы (10), рассматривая свободные члены ее как коэффициенты при :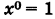

Последний столбец 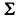содержит суммы элементов соответствующих строк таблицы; этот столбец служит для контроля вычислений.

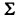
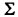
Считая отмеченный коэффициент 2 ведущим и деля на этот коэффициент все элементы первой строки таблицы (включая и входящий в столбец ), получаем коэффициенты первого приведенного уравнения (см. табл.). Текущий контроль вычислений осуществляется тем, что элемент из столбца равен сумме всех остальных элементов этой строки. Этим заканчивается заполнение раздела I таблицы.

Далее, используя формулу (6), подсчитываем коэффициенты укороченной системы, не содержащей неизвестного xv Для наглядности будем называть строку, содержащую коэффициенты приведенного уравнения, приведенной, а столбец, содержащий ведущий элемент раздела, — ведущим. Тогда на основании формулы (6) справедливо правило: преобразованные коэффициенты схемы Гаусса, равны ее прежним коэффициентам минус произведение «проекций» их на соответствующие приведенную строку и ведущий столбец таблицы. Пользуясь этим, заполняем раздел II таблицы, включая контрольный столбец. Для удобства вычислении в качестве ведущего коэффициента раздела П берем элемент 8 (см. табл.).

Аналогично производится заполнение раздела III таблицы. Этим заканчивается прямой ход схемы Гаусса.

Неизвестные 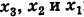последовательно определяются из приведенных уравнений

(обратный ход). Результаты обратного хода помещены в разделе IV таблицы.

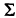
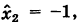
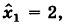
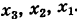
Заметим, что если в качестве свободных членов взять элементы столбца , то для неизвестных получатся значения превышающие на единицу значения неизвестных Этим обеспечивается заключительный контроль вычислений.

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Метод Гаусса — определение и вычисление
Прямая линия на плоскости и в пространстве
Плоскость в трехмерном пространстве
Функция одной переменной
Ряды в математике
Дифференциальные уравнения с примерами
Обратная матрица — определение и нахождение
Ранг матрицы — определение и вычисление

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Решение системы уравнений методом Крамера.Скачать

Решение СЛАУ 3-его порядка методом Гаусса, пример № 11

СЛАУ 3-его порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12
СЛАУ 4-ого порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12

Условие

5 x ₁	— x ₂	— x ₃	= 0
x ₁	+ 2 x ₂	+ 3 x ₃	= 14
4 x ₁	+ 3 x ₂	+ 2 x ₃	= 16

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по геометрии и другим предметам!

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 3 × 4, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.