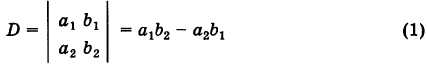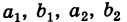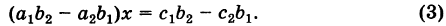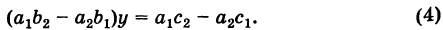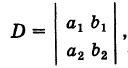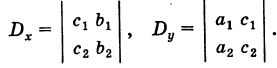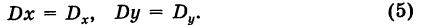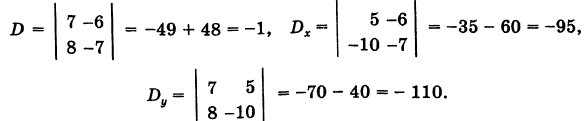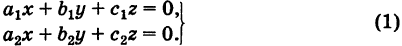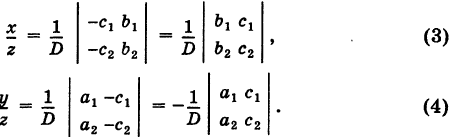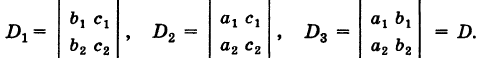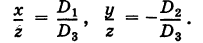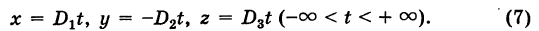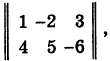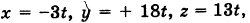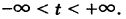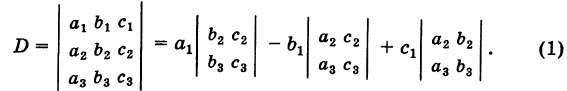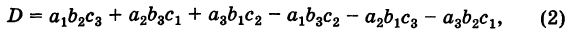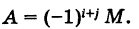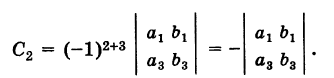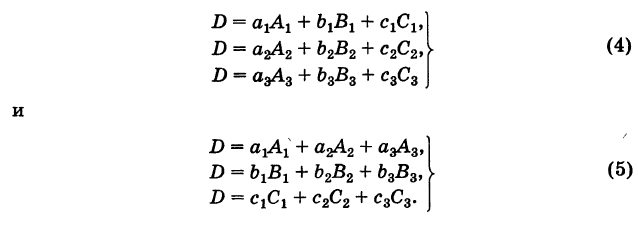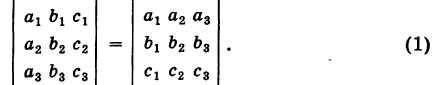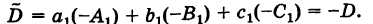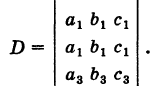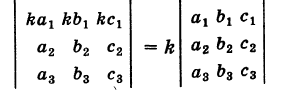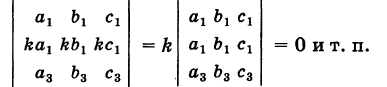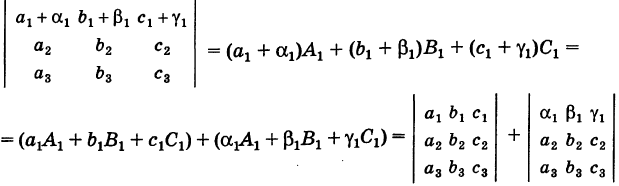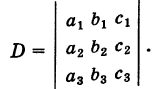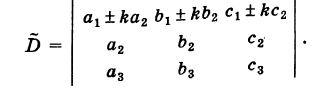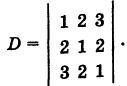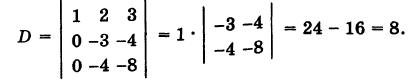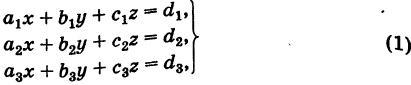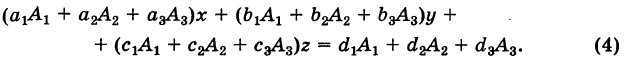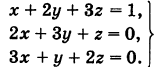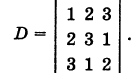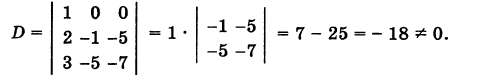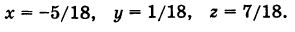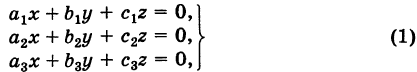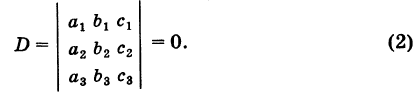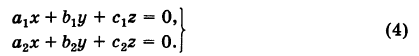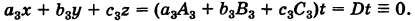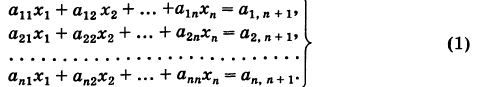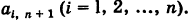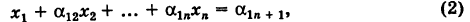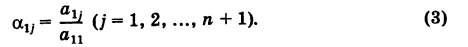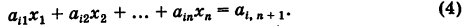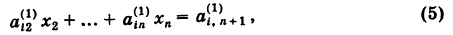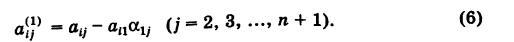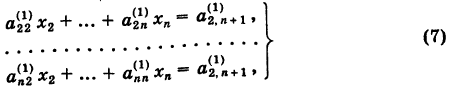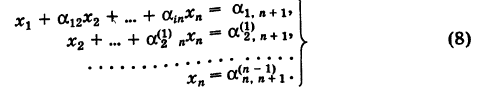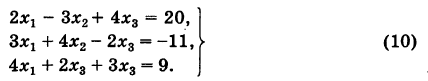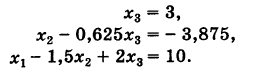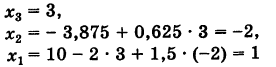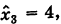- Формулы Крамера
- Три случая при решении систем линейных уравнений
- Примеры решения систем линейных уравнений методом Крамера
- Применить метод Крамера самостоятельно, а затем посмотреть решения
- К началу страницы
- Пройти тест по теме Системы линейных уравнений
- Продолжаем решать системы методом Крамера вместе
- Определители второго и третьего порядков и их свойства с примерами решения
- Определители второго порядка
- Система двух однородных уравнений с тремя неизвестными
- Определители третьего порядка
- Основные свойства определителей
- Система трех линейных уравнений
- Однородная система трех линейных уравнений
- Система линейных уравнений с многими неизвестными. Метод Гаусса
- Решить систему из 3-х уравнений с 3-мя неизвестными онлайн
- Калькулятор
- Инструкция
- Что такое система из 3-х уравнений с 3-мя неизвестными
- Решение задач по математике онлайн
- Калькулятор онлайн. Решение систем линейных алгебраических уравнений (СЛАУ) Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
- Немного теории.
- Системы линейных алгебраических уравнений
- Основные определения
- Формы записи СЛАУ
- Критерий совместности СЛАУ
- Формулы Крамера
- Однородные системы
- Неоднородные системы
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Формулы Крамера
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается 
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:


Формулы Крамера для нахождения неизвестных:

Найти значения 


Этот вывод следует из следующей теоремы.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:
Итак, решение системы (2):
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Видео:Решение системы уравнений методом Крамера.Скачать

Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
*
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
* 
** 
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
*
** 
Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
Видео:Решение системы трех уравнений по формулам КрамераСкачать

Примеры решения систем линейных уравнений методом Крамера
Пусть дана система

На основании теоремы Крамера

…………. 
где 
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Применить метод Крамера самостоятельно, а затем посмотреть решения
Пример 4. Решить систему линейных уравнений:

Пример 5. Решить систему линейных уравнений методом Крамера:

Видео:Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать

К началу страницы
Видео:Система с тремя переменнымиСкачать

Пройти тест по теме Системы линейных уравнений
Видео:Решение системы уравнений методом Крамера 2x2Скачать

Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.
Пример 7. Решить систему линейных уравнений методом Крамера:
Здесь a — некоторое вещественное число. Решение. Находим определитель системы:
Находим определители при неизвестных
По формулам Крамера находим:


Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
По формулам Крамера находим:



И, наконец, система четырёх уравнений с четырьмя неизвестными.
Пример 9. Решить систему линейных уравнений методом Крамера:

Внимание! Методы вычисления определителей четвёртого порядка здесь объясняться не будут. За этим — на соответствующий раздел сайта. Но небольшие комментарии будут. Решение. Находим определитель системы:
Небольшой комментарий. В первоначальном определителе из элементов второй строки были вычтены элементы четвёртой строки, из элементов третьей строки — элементы четвёртой строки, умноженной на 2, из элементов четвёртой строки — элементы первой строки, умноженной на 2. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители при неизвестных
Для преобразований определителя при четвёртом неизвестном из элементов первой строки были вычтены элементы четвёртой строки.
По формулам Крамера находим:




Итак, решение системы — (1; 1; -1; -1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Самые внимательные, наверное, заметили, что в статье не было примеров решения неопределённых систем линейных уравнений. А всё потому, что методом Крамера решить такие системы невозможно, можно лишь констатировать, что система неопределённа. Решения таких систем даёт метод Гаусса.
Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Определители второго и третьего порядков и их свойства с примерами решения
Содержание:
Определители второго порядка:
Под определителем (детерминантом) второго порядка понимается выражение
Числа
Формула (1) дает правило «развертывания» определителя второго порядка, а именно: определитель второго порядка равен разности произведений его элементов первой и второй диагоналей.
Видео:определители 2-го и 3-го порядка. метод Крамера для решения систем линейных уравненийСкачать

Определители второго порядка
С помощью определителей второго порядка удобно решать линейные системы двух уравнений с двумя неизвестными:
Такую линейную систему, в которой свободные члены находятся в правых частях, для определенности мы будем называть стандартной.
Под решением системы (2) понимается всякая пара чисел (х, у), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным. Аналогично вводится понятие решения для системы, содержащей п неизвестных 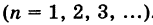
Для нахождения решений системы (2) применим метод исключения. Умножая первое уравнение системы (2) на 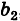
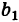
Аналогично, умножая первое уравнение системы (2) на а2 второе — на 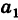
Введем определитель системы
а также дополнительные определители
Заметим, что дополнительные определители Dx и Dy получаются из определителя системы D путем замены коэффициентов при указанном неизвестном на соответствующие свободные члены.
Уравнения (3) и (4) принимают вид
Если 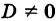
Замечание. Если определитель D = 0, то система (2) или не имеет решений (т. е. несовместна), или имеет бесконечно много решений (т. е. система неопределенная).
Пример:
Решение:
Имеем
Отсюда на основании формул Крамера (6) получаем
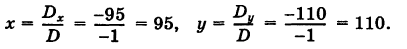
Видео:Решение системы уравнений методом Крамера 4x4Скачать

Система двух однородных уравнений с тремя неизвестными
Рассмотрим однородную систему
Эта система всегда совместна, так как, очевидно, имеет нулевое решение х = 0, у = 0, z = 0. Однако интересно найти не н у л е в ы е решения (х, у, z) системы (1). Пусть, например, 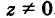
Тогда систему (1) можно переписать в виде
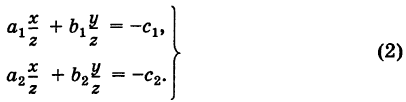
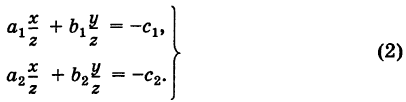
Введем в рассмотрение матрицу коэффициентов системы (1)
Определители второго порядка 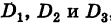
Используя эти обозначения, уравнения (3) и (4) можно переписать в следующем виде:
Равенства (6), очевидно, справедливы также и для нулевого решения.
Таким образом, имеем следующее правило: неизвестные однородной системы (1) пропорциональны соответствующим минорам ее матрицы коэффициентов, взятым с надлежащими знаками.
Обозначая через t коэффициент пропорциональности для отношений (6), получим полную систему решений системы (1):
При выводе формул (7) мы предполагали, что 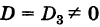
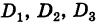
Замечание. Если все миноры 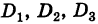
Пример:
Решение:
Составляя матрицу коэффициентов
находим ее миноры: 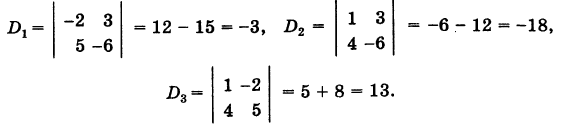
где
Простейшее ненулевое решение системы (1), получающееся при t — 1, есть х = -3, у = 18, z = 13.
Видео:2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Определители третьего порядка
Числа 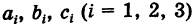
Раскрывая определители второго порядка (миноры) в формуле (1) и собирая члены с одинаковыми знаками, получаем, что определитель третьего порядка представляет собой знакопеременную сумму шести слагаемых:
из которых три берутся со знаком плюс, а три — со знаком минус.
Пример:
Решение:
Используя формулу (1), имеем 
Определение: Под минором элемента определителя третьего порядка понимается определитель младшего (второго) порядка, получающийся из данного определителя в результате вычеркивания строки и столбца, содержащих данный элемент.
Например, для определителя (3) минором его элемента 2, стоящего во второй строке и в первом столбце, является определитель 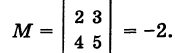
Определение: Алгебраическим дополнением (минором со знаком) элемента определителя третьего порядка называется минор этого элемента, взятый со знаком плюс, если элемент занимает четное место у и со знаком минус, если его место нечетное.
Таким образом, если М есть минор элемента определителя, a i и j — соответственно номер строки и номер столбца, на пересечении которых находится данный элемент, то его алгебраическое дополнение есть
Например, для элемента с2 определителя (1), находящегося во второй строке и в третьем столбце, его алгебраическое дополнение есть
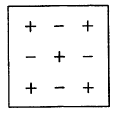
Соответствующие знаки, приписываемые при этом минорам элементов определителя, можно задать таблицей
В дальнейшем алгебраические дополнения элементов определителя с буквенными элементами условимся обозначать соответствующими прописными (большими) буквами.
Теорема Разложения: Определитель третьего порядка равен сумме парных произведений элементов какого-либо ряда его на их алгебраические дополнения (под рядом понимается строка или столбец).
Таким образом, для определителя (1) справедливы шесть разложений:
Легко проверить, что формулы (4) и (5) дают одно и то же выражение (2), принятое за определение.
Замечание. С помощью формул типа (4) или (5), по индукции, можно ввести определители высших порядков.
Видео:10. Метод Крамера решения систем линейных уравнений.Скачать

Основные свойства определителей
При формулировках мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка.
I. (Равноправность строк и столбцов.) Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, т. е.
Действительно, разлагая первый определитель по элементам первой строки, а второй — по элементам первого столбца, в силу теоремы разложения мы получим один и тот же результат.
II. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на обратный.
Пусть, например, в определителе 
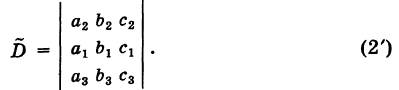
Аналогичное положение получается и в других случаях.
Следствие 1. Определитель, у которого два параллельных ряда одинаковы, равен нулю.
В самом деле, пусть, например,
Переставляя первую и вторую строки определителя, в силу теоремы получим определитель -D. Но очевидно, эта операция не изменяет определитель D, поэтому -D = D и, следовательно, D = 0.
Следствие 2. Сумма парных произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю, т. е. для определителя (2) имеем 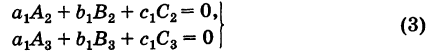
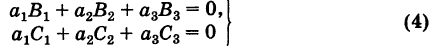
Левые части всех соотношений (3) и (4) представляют собой разложения соответствующих определителей третьего порядка, содержащих два одинаковых параллельных ряда и, следовательно, равны нулю. Например, 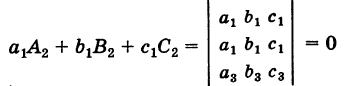
III. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя, т. е.
Это свойство непосредственно вытекает из разложения определителя по элементам соответствующего ряда.
Следствие 1. Если все элементы какого-либо ряда определителя равны нулю, то определитель равен нулю.
Следствие 2. Если элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда его, то определитель равен нулю.
Например, имеем
IV. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Следствие. Величина определителя не изменится, если /с элементам какого-либо ряда его прибавить (или отнять) числа, пропорциональные соответствующим элементам параллельного ряда с одним и тем же коэффициентом пропорциональности (так называемые «элементарные преобразования определителя»).
Рассмотрим, например, определители
Используя свойства IV и III, будем иметь 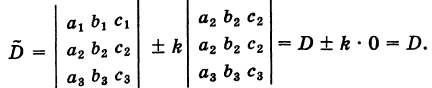
Пример:
Вычислить симметричный определитель
Решение:
Вычитая из второй строки удвоенную первую строку, а из третьей строки утроенную первую строку, получим
Система трех линейных уравнений
Рассмотрим стандартную линейную систему трех уравнений
свободные члены которых находятся в правых частях. Под решением системы понимается всякая тройка чисел (х, у, г), удовлетворяющая этой системе. Введем определитель системы
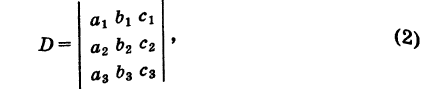
Последовательно умножая уравнения системы (1) на алгебраические дополнения 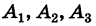
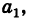
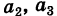
Отсюда, применяя теорему разложения и следствие 2 к свойству II, будем иметь 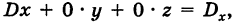

Если определитель системы 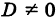
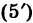
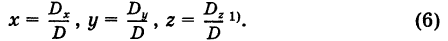
Замечание. Если определитель системы D = 0, то система (1) или несовместна, или имеет бесконечно много решений.
Пример:
Решение:
Вычитая из второго столбца удвоенный первый столбец, а из третьего столбца утроенный первый столбец, получим
Для дополнительных определителей находим следующие значения: 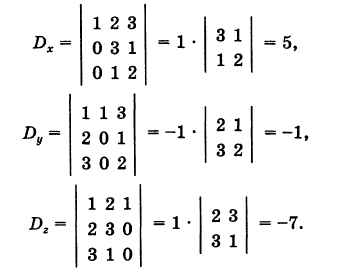
Однородная система трех линейных уравнений
Рассмотрим линейную систему
свободные члены которой равны нулю. Такая линейная система называется однородной.
Однородная линейная система (1), очевидно, допускает нулевое решение х = 0, у = 0, z = 0 и, следовательно, всегда совместна.
Интересно выяснить случаи, когда однородная система имеет ненулевые решения.
Теорема: Линейная однородная система трех линейных уравнений с тремя неизвестными имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т. е.
Доказательство: Пусть система (1) имеет ненулевое решение 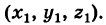
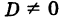
Пусть D = 0. Тогда линейная система (1) либо несовместна, либо имеет бесконечно много решений. Но наша система совместна, так как имеется нулевое решение. Следовательно, система (1) допускает бесконечно много решений, в том числе и ненулевые.
Замечание. Укажем способ нахождения ненулевых решений однородной системы (1) в типичном случае.
Пусть определитель системы D = 0, но не все его миноры второго порядка равны нулю.
Мы будем предполагать, что
(этого всегда можно добиться с помощью перестановки уравнений и изменения нумерации неизвестных).
Рассмотрим подсистему, состоящую из двух первых уравнений системы (1):
В силу решения этой системы имеют вид
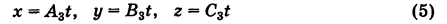
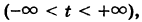
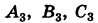
Следовательно, формулы (5), где t произвольно, дают все решения полной системы (1).
Геометрически уравнения системы (1) представляют собой уравнения трех плоскостей в пространстве Oxyz. Если определитель 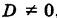
Система линейных уравнений с многими неизвестными. Метод Гаусса
Рассмотрим систему 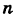
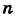
Здесь для коэффициентов системы введена двойная индексация, а именно: у коэффициента 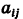
Наиболее простой метод решения системы (1) — это метод исключения. Мы изложим его в форме схемы Гаусса (обычно называемой методом Гаусса).
Пусть для определенности 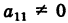
Рассмотрим i-e уравнение системы (1):
Для исключения xx из этого уравнения умножим приведенное уравнение (2) на ап и полученное уравнение вычтем из уравнения (4). Тогда будем иметь
Таким образом, получаем укороченную систему
коэффициенты которой определяются по формулам (6).
Если ее ведущий коэффициент 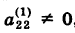
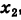
Для определения неизвестных 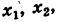
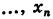
Отсюда последовательно находим неизвестные (обратный ход) 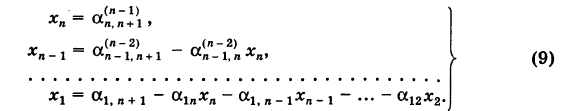
Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.
Пример:
Методом Гаусса решить систему
Решение:
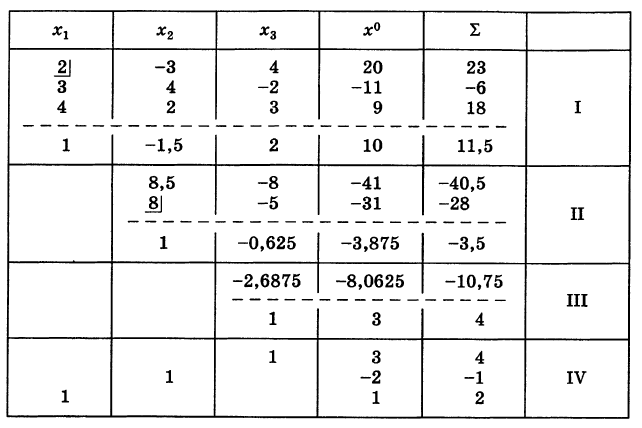
Составляем таблицу коэффициентов системы (10), рассматривая свободные члены ее как коэффициенты при 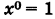
Последний столбец 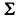
Считая отмеченный коэффициент 2 ведущим и деля на этот коэффициент все элементы первой строки таблицы (включая и входящий в столбец 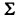
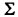
Далее, используя формулу (6), подсчитываем коэффициенты укороченной системы, не содержащей неизвестного xv Для наглядности будем называть строку, содержащую коэффициенты приведенного уравнения, приведенной, а столбец, содержащий ведущий элемент раздела, — ведущим. Тогда на основании формулы (6) справедливо правило: преобразованные коэффициенты схемы Гаусса, равны ее прежним коэффициентам минус произведение «проекций» их на соответствующие приведенную строку и ведущий столбец таблицы. Пользуясь этим, заполняем раздел II таблицы, включая контрольный столбец. Для удобства вычислении в качестве ведущего коэффициента раздела П берем элемент 8 (см. табл.).
Аналогично производится заполнение раздела III таблицы. Этим заканчивается прямой ход схемы Гаусса.
Неизвестные 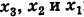
(обратный ход). Результаты обратного хода помещены в разделе IV таблицы.
Заметим, что если в качестве свободных членов взять элементы столбца 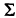
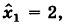
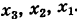
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Решение системы уравнений методом ГауссаСкачать

Решить систему из 3-х уравнений с 3-мя неизвестными онлайн
Этот онлайн калькулятор предназначен для решения систем из трёх уравнений с тремя неизвестными. Вы можете быть уверены, что калькулятор выдаёт точный результат.
Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Калькулятор
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Инструкция
Примечание: π записывается как pi; корень квадратный как sqrt().
Шаг 1. Введите в поля три уравнения.
Шаг 2. Нажмите кнопку “Решить систему”.
Шаг 3. Получите точный результат.
В калькулятор нужно вводить только латинские буквы и любые цифры с клавиатуры.
Видео:Тема: Системы линейных уравнений. Урок: Решение системы трёх линейных уравнений с тремя неизвестнымиСкачать

Что такое система из 3-х уравнений с 3-мя неизвестными
Решение систем из трёх уравнений с тремя неизвестными – это то же линейное уравнение, которое, чаще всего решается методом Крамера. Однако метод Крамера можно использовать только в том случае, если определитель системы не равняется нулю. Если же определитель системы равен нулю, тогда нельзя использовать этот метод.
Следуя теореме Крамера, в таких уравнениях может быть три случая:
- У системы уравнений есть всего навсего одно решение.
- У системы уравнений имеется бесконечное множество решений.
- У системы уравнений нет решений.
Средняя оценка 2.7 / 5. Количество оценок: 3
Видео:Система трех линейных уравнений с тремя неизвестными. Правило Крамера. Свойства определителя.Скачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )
Ввод: -1,15
Результат: ( -115 )
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!
RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )
Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.
Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.
СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.
Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
Однородные системы
Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).
Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.
Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.