Решение систем нелинейных уравнений octave (4 видео)

Содержание

Моделирование динамических систем: решение нелинейных уравнений
1. Постановка задачи
2. Уравнение, которого нет
3. Принципы численного решения нелинейных уравнений
4. Определяем параметры траектории пушечного ядра
Решение двух нелинейных уравнений в Octave
IT Novella
Возможности СКМ Octave
Система компьютерной математики Octave
Системы компьютерной математики
Простейшие операции
Рассмотрим пример
Элементарные математические функции
Экспоненциальные функции
Условный оператор
Матрично-векторные вычисления
Создание матриц
Возможности СКМ Octave
🌟 Видео

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Моделирование динамических систем: решение нелинейных уравнений

Конечной целью математического моделирования в любой области знаний является получение количественных характеристик исследуемого объекта. Некоторые параметры пушки, стрельбу из которой мы моделировали в прошлый раз, были заданы в условии задачи: начальная скорость снаряда, его калибр и материал, из которого он изготовлен. Угол наклона ствола можно отнести к варьируемым параметрам: любое серьезное орудие допускает наводку, в том числе и в вертикальной плоскости.

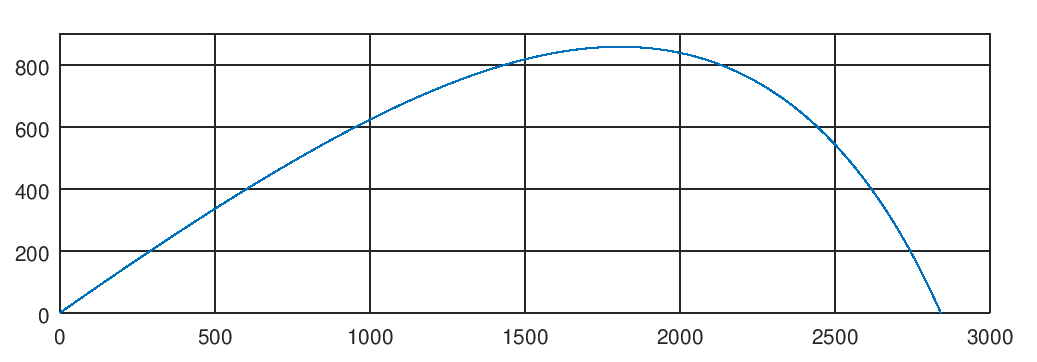
На выходе мы получили траекторию полета снаряда, что дает нам ориентировочные представления о характеристиках орудия: при заданных параметрах мы получили дальность стрельбы чуть более 2,5 км и высоту подъема снаряда чуть выше 800 метров. Точнее мы сказать не можем, вернее можем, если с карандашиком по сетке определим координаты нужных точек на графике. Но это, как известно, не наш метод. Хорошо бы получить эти данные с точностью, обеспечиваемой используемыми нами инструментами и без ручного труда. Вот об этом мы сегодня и поговорим.

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

1. Постановка задачи

Итак, построенная в прошлый раз математическая модель позволяет нам, для любого момента времени, определить координаты и скорость снаряда. По сути мы получили функции, которые позволяют вычислить следующие параметры траектории:

как функции времени. Высота полета снаряда это y(t). Если мы определим в какой момент времени высота становится равна нулю, то есть решим уравнение

относительно времени, то мы найдем момент времени в который снаряд упал на землю. Координата и будет дальность полета снаряда.

Как найти максимальную высоту подъема снаряда? Из графика траектории видно, что по мере подъема снаряда его траектория становится всё более и более пологой, пока в экстремальной точке скорость на мгновение становится горизонтальной и дальше снаряд движется вниз.

Говоря языком математики, необходимо найти точку экстремума функции . А что надо для этого сделать? Приравнять к нулю её производную! В данном случае производную по времени, то есть решить уравнение

ведь производная от вертикальной координаты по времени есть вертикальная проекция скорости. Корень этого уравнения, есть момент времени, когда снаряд достигнет максимальной высоты. Соответственно, интересующая нас высота

Просто? Более чем.

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

2. Уравнение, которого нет

И вот тут котенка Гава, как известно, ждут неприятности. Начнем с того, что даже если уравнение задано в виде формулы (аналитически) не всегда удается найти его решение. Вот например

Как вам? Простенько, но попробуйте найти икс, используя всё то, чему вас учили в школе. То-то же…

Введем замену , тогда
begin
&u , e^ = 1 \
&u , e^ = e^ \
&-u , e^ = -e^
end
Пусть теперь , тогда

Теперь делаем финт ушами. Математики прошлого хорошо поработали за нас. Если задана функция вида

то обратная ей функция, называется W-функцией Ламберта.

Не в даваясь в теорию ФКП, в которой я мало смыслю, скажу, что число попадает в интервал в котором функция Ламберта многозначна, значит корня будет два

откуда, раскручивая назад все замены получаем ответ

Приближенно этот ужас равен

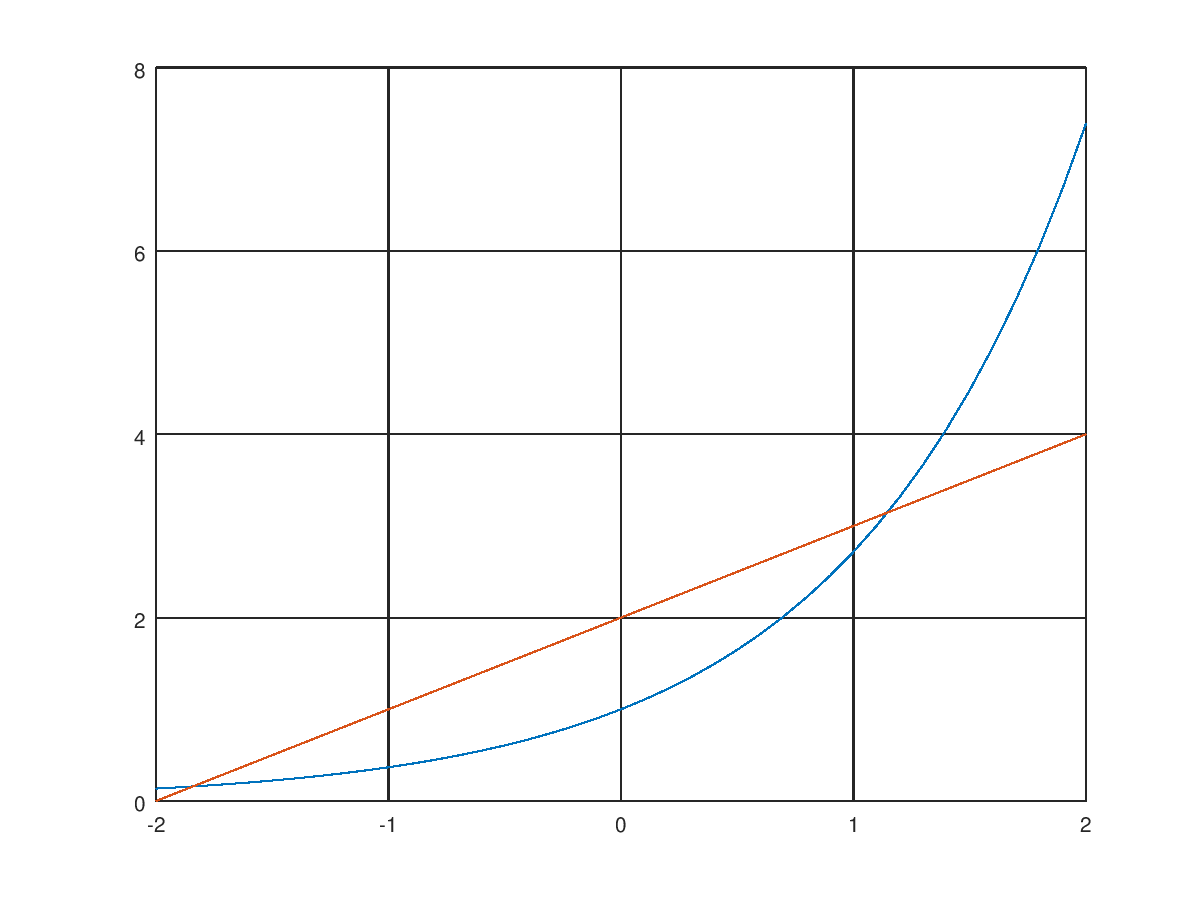
Решение такого уравнения придется искать численно, тем более что очевидно его графическое решение

В случае с моделью пушки всё несколько коварнее — наше уравнение задано даже не формулой. Оно задано, грубо говоря, таблицей значений фазовых координат, полученных для вполне конкретных параметров выстрела. У нас нет уравнения!

Ну так нам никто не мешает, чёрт возьми, это уравнение построить. Но, прежде чем начать писать скрипты, хочу извинится перед читателем, что ввёл его в заблуждение. В одном файле скрипта Octave можно размещать несколько функций, и имя файле на обязательно должно совпадать с именем функции. Достаточно, чтобы скрипт не начинался с определения функции.

Создадим новый скрипт в том же каталоге, где расположены файлы ballistics.m, f.m и f_air.m. Назовем его, например cannon.m. Для начала зададимся параметрами снаряда, начальной скоростью и направлением выстрела

А теперь напишем функцию, которая будет вычислять значения фазовых координат для произвольного момента времени

Обратите внимание, теперь в качестве моментов времени, передаваемых функции решения уравнения мы берем всего два значения: начальный момент времени (t = 0) и интересующий нас момент времени. Соответственно, переменная solv будет содержать два вектора фазовых координат: начальный и тот который нам нужен. Собираем все компоненты конечной точки фазовой траектории в вектор Y и возвращаем его значение из функции.

Теперь нам ничего не стоит определить зависимость высоты полета снаряда от времени

протестируем полученную функцию

При запуске скрипта на исполнение мы увидим в командном окне следующий вывод

Отлично, функция работает! Аналогично определим и функцию вычисления горизонтальной дальности

Видно, что для вычисления высоты и дальности мы каждый раз интегрируем уравнения движения, от начального до интересующего нас момента времени. Таким образом мы получили зависимость, не выражаемую конкретной формулой. Это довольно круто.

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

3. Принципы численного решения нелинейных уравнений

Методы численного решения нелинейных и трансцендентных уравнений заточены под решение уравнений вида

К такой форме легко привести любое уравнение. Например

где . Корни этого, эквивалентного уравнения, равны корням исходного. Если мы построим график функции f(x), то увидим такую картинку

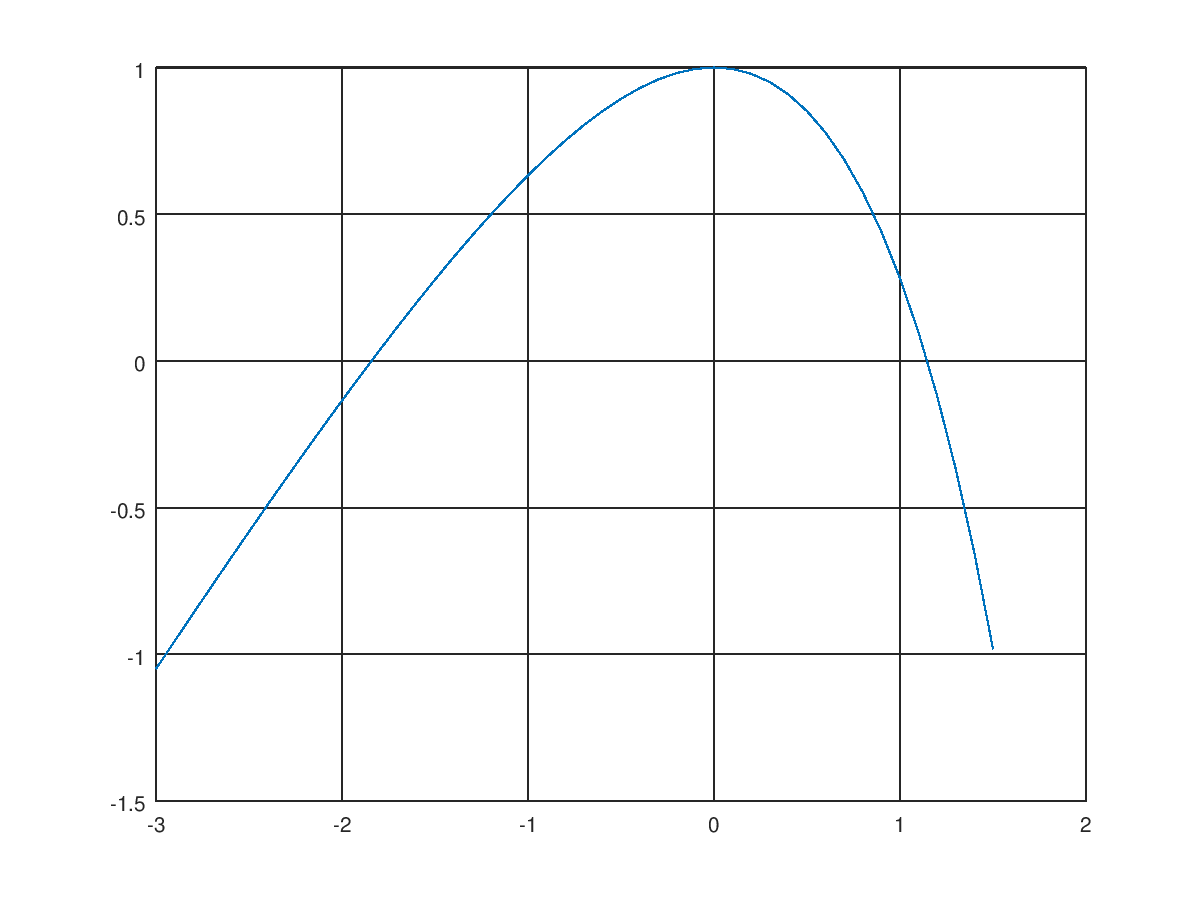
корни уравнения это значения аргумента в тех точках, где график пересекает ось x.

Все методы численного решения таких уравнений включают в себя два этапа:

Поиск начального приближения корня
Уточнение корня с заданной погрешностью

Под начальным приближением понимают значение аргумента f(x), максимально близкое к корню, либо достаточно близкое, чтобы обеспечить сходимость метода за разумное количество итераций.

Простейшим методом является метод простых итераций. Для применения этого метода уравнение преобразуют к виду

и выполняю расчеты по рекуррентной формуле

В нашем примере

Посмотрим на график. У уравнения два корня. Найдем крайний левый корень, выбрав в качестве начального приближения

Ага, видно, что начиная с шестой итерации четвертый знак получающегося числа остается неизменным. Значит мы нашли корень уравнения с погрешностью менее 10 -4 на шестой итерации.

Все бы хорошо, но метод простых итераций не всегда сходится. Попробуйте найти второй корень этого уравнения, задавшись любым, сколь угодно близким начальным приближением — у вас ничего не выйдет: каждое новое значение будет уходить от корня всё дальше и дальше. Сходимости метода можно добиться, существуют способы, но на практике это существенно осложняет нам жизнь. Поэтому для нахождения второго корня применим другой метод. Разложим исследуемую функцию в ряд Тейлора, в окрестности начального приближения

Ограничимся членами первого порядка малости, заменив саму функцию f(x) касательной к её графику в точке x₀

и приравняв полученное выражение к нулю, решим его относительно x

Получаем итерационную формулу

В нашем примере

В качестве начального приближения берем и пытаемся выполнять итерации

Как видно, этот метод сошелся за четыре итерации с точностью до четырех знаков. Этот метод называют методом Ньютона. Его достоинством является быстрая сходимость. Среди недостатков: высокая чувствительность к точности начального приближения и необходимость вычислять производную левой части уравнения. В случае, когда для уравнения нет аналитического выражения, приходится прибегать к мерзкой операции численного дифференцирования, что не всегда удобно и возможно.

Эти примеры я привел, чтобы объяснить общий принцип. Кроме этих двух методов существует ещё масса методов, например:

Метод бисекции — отличается гарантированной сходимостью, однако с довольно низкой скоростью
Метод хорд — не требует вычисления производной функции, обладает неплохой скоростью сходимости

Все перечисленные методы требуют предварительной подготовки, в виде поиска начального приближения или интервала изоляции корня — интервала изменения аргумента f(x), на границах которого функция меняет знак. В этом случае можно с уверенность сказать (при условии непрерывности функции!) что внутри интервала изоляции есть хотя бы один корень.

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

4. Определяем параметры траектории пушечного ядра

Итак, найдем момент времени, когда снаряд упадет на землю. Прежде всего, определим интервал изоляции корня

Делаем это исходя из физического смысла задачи — после сразу выстрела высота полета снаряда неотрицательна. Перебираем все моменты времени, начиная от нуля, до тех пор, пока высота не станет отрицательна. Перебираем с достаточно крупным шагом (1 секунда) чтобы процедура не была слишком длительной, ведь на каждом шаге мы заново интегрируем дифференциальные уравнения движения, что весьма накладно сточки зрения вычислительных затрат. Как только высота станет отрицательной, заканчиваем перебор. Корень уравнения h(t) = 0 находится где-то внутри интервала [a, b]. Начальное приближение берем в середине этого интервала

Теперь отдаем уравнение на съедение процедуре решения нелинейных уравнений Octave

Функция fsolve() на вход принимает функцию, описывающую левую часть уравнения f(x) = 0 и значение начального приближения. Возвращает значение корня, вычисленное с заданной точностью. С какой точностью? Пока не будем задаваться этим вопросом и воспользуемся настройками по-умолчанию, на данном этапе они нас устраивают.

Получив значение момента времени падения, вычисляем дистанцию от позиции стрельбы

Аналогичным образом находим момент времени когда обнуляется вертикальная проекция скорости и вычисляем высоту полета снаряда в этот момент

В командном окне можно увидеть результаты работы программы

а также посмотреть, с какой точностью были решены уравнения

Для наших учебных целей точность вполне приемлема.

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Решение двух нелинейных уравнений в Octave

Я пытаюсь решить следующие два уравнения, используя Octave:

Я использовал следующий код:

ws , wp , As и Ap приведены в качестве 1.5708 , 0.31416 , 0.5 , 45 соответственно.

Но я получаю следующую ошибку:

Ошибка: исключение Python: NotImplementedError: не удалось решить
126491*(pi*(3*10**N*sqrt(314311)*pi**(-N)/1223)**(1/N)/2)**(2*N) — 126495
произошло в строке 7 кода кода Python:
d = sp.solve(eqs, *symbols, dict=True)

Что я должен сделать, чтобы решить эту проблему?

Редактировать:

Я немного изменил уравнения.

И теперь я получаю эту ошибку:

error: Исключение Python: AttributeError: MutableDenseMatrix не имеет атрибута is_Relational .
произошел в строке 3 кода кода Python:
if arg.is_Relational:

Глядя на уравнения, с неизвестными в базе и показателем того же термина, очень важно, что нет никакого символического решения, которое можно найти. Я дал упрощенную систему (2/x)^y = 4, (3/x)^y = 5 для пары символических решателей, ни одна из которых не получила от нее ничего. Таким образом, единственный способ решить это численно (что имеет смысл, потому что четыре известных параметра у вас есть некоторые числа с плавающей запятой). Цифровой решатель Octave для этой цели является fsolve . Пример использования:

(Здесь [1; 1] — начальное предположение.) Вывод

Видео:4.2 Решение систем нелинейных уравнений. МетодыСкачать

IT Novella

После нажатия клавиши на экране появится результат выполнения команды

Функция rand позволяет генерировать случайные числа из нтервала (0,1).

Если функция вызывается без аргументов, то будет создано случайное число.

Если функция имеет один аргумент rand(m), то будет создана квадратная матрица размерности mхm.

Если передать два аргумента rand(m,n), то будет создана матрица размерности $ m times n $

В теории линейной алгебры выделяют специальные виды матриц.

Создать такие матрицы в Octave позволяют следующие функции:

ones(m),ones(m,n)
Функция генерирует матрицу с элементами 1 (количество аргументов трактуется аналогично eye).octave:18> = ones(2)

zeros(m), zeros(m,n)
Функция генерирует нулевую матрицу (количество аргументов трактуется аналогично eye).octave:29> Z = zeros(2)

diag(v, k)
Функция генерирует диагональную матрицу с элементами вектора v на диагонали k. Аргумент k выступает в качестве опции:k=0 означает главную диагональ, при k > 0 элементы вектора v ставятся на k-ую диагональ выше, а при k D = diag([1 2 3])

Возможности СКМ Octave

GNU Octave — высокоуровневый язык программирования, предназначенный прежде всего для численных расчётов. Он предоставляет удобный интерфейс командной строки для численного решения линейных и нелинейных задач, а также для выполнения других численных экспериментов. Кроме того, GNU Octave — свободно распространяемое программное обеспечение.

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Система компьютерной математики Octave

Системы компьютерной математики

Система компьютерной алгебры (computer algebra system, CAS) — программное приложение для символьных вычислений,

т.е. для выполнения преобразований и работы с математическими выражениями в аналитической (символьной) форме.

GNU Octave

GNU Octave — это свободно распространяемый язык программирования высокого уровня, ориентированный на проведение численных расчетов, и по сути являющийся альтернативой коммерческому пакету MatLab.

Простейшие операции

Простейшие арифметические операции в Octave выполняются с помощью следующих операторов:

Рассмотрим пример

Решить систему линейных алгебраических уравнений:

Для решения СЛАУ в окне интерпретатора Octave последовательно введём следующие команды:

Элементарные математические функции

Экспоненциальные функции

Примеры применения экспоненциальных функций:

Целочисленные функции

Примеры работы с целочисленными функциями:

Комплексные числа

Ввод комплексного числа производится в формате:

действительная часть + i * мнимая часть

действительная часть + j * мнимая часть

Примеры записи комплексных чисел в Octave

Функции работы с комплексными числами

Примеры использования функций

Основные операторы в Octave

Условный оператор

Обычный условный оператор имеет вид:

Обычный оператор if работает по следующему алгоритму:

если условие истинно, то выполняются операторы1, если ложно — операторы2.

Рассмотрим работу условного оператора на примере.

Пример:даны вещественные числа x и y. Определить принадлежит ли точка с координатами (x;y) заштрихованной части плоскости.

Текст программы и результат её работы

Оператор альтернативного выбора

Оператор switch

Оператор switch работает следующим образом: если значение параметра равно значение1, то выполняются опреаторы1, иначе если параметр равен значение2, то выполняются операторы2. В противном случае, если значение параметра совпадает с значение3, то выполняются операторы3 и т.д. Если значение параметра не совпадает ни с одним из значений в группах case, то выполняются операторы, идущие после служебного слова otherwise.

Рассмотрим использование оператора switch на примере:

Вывести на экран название дня недели, соответствующее заданному числу D, при условии, что в месяце 31 день и первое число — понедельник.

Матрично-векторные вычисления

Создание матриц

Любую матрицу или вектор с заданными элементами в Octave можно создать путем перечисления

этих элементов в квадратных скобках ([ ]), разделяя столбцы пробелом или запятой, строки

знаком ”точка с запятой”

octave:1>A=[1 3 5; 2 4 6]

После нажатия клавиши на экране появится результат выполнения команды

Функция rand позволяет генерировать случайные числа из нтервала (0,1).

Если функция вызывается без аргументов, то будет создано случайное число.

Если функция имеет один аргумент rand(m), то будет создана квадратная матрица размерности mхm.

Если передать два аргумента rand(m,n), то будет создана матрица размерности $ m times n $

В теории линейной алгебры выделяют специальные виды матриц.

Создать такие матрицы в Octave позволяют следующие функции:

ones(m),ones(m,n)
Функция генерирует матрицу с элементами 1 (количество аргументов трактуется аналогично eye).octave:18> = ones(2)

zeros(m), zeros(m,n)
Функция генерирует нулевую матрицу (количество аргументов трактуется аналогично eye).octave:29> Z = zeros(2)

diag(v, k)
Функция генерирует диагональную матрицу с элементами вектора v на диагонали k. Аргумент k выступает в качестве опции:k=0 означает главную диагональ, при k > 0 элементы вектора v ставятся на k-ую диагональ выше, а при k D = diag([1 2 3])