Решение систем нелинейных уравнений методом ньютона excel

Как видно, процесс нахождения корней нелинейного уравнения методом Ньютона состоит из следующих этапов:

1. Получения шаблона.
2. Уточнение интервалов в ячейках B2 , B3 .
3. Замена в формуле ЕСЛИ запятую ( , ) на точку с запятой ( ; ).
4. Копирование строки итераций до требуемой точности (столбец E ).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — значение первой производной dF(X) , столбец E — точность eps .

Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Решение уравнений средствами EXCEL

Идея метода

Нелинейные уравнения

Аналитическое решение нелинейных уравнений существует только для узкого круга типов уравнений. Доказано, что алгебраические уравнения выше четвертой степени неразрешимы в элементарных функциях. Поэтому решение уравнения сводят к численному решению.

Нахождение приближенного решения проводят в два этапа. На первом этапе производится отделение корней – поиск интервалов, в которых содержится только по одному корню. Второй этап решения связан с уточнением корня в выбранном интервале (определением значения корня с заданной точностью).

В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)≤0, то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x) = x 3 -6x+2 = 0 видим, что при x →∞ f(x)>0, при x → — ∞ f(x) n -6 ) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.

Метод Ньютона

Данный метод еще называют методом касательных, т.к. основная идея метода заключается в последовательном построении касательных в точках, выбираемых по определенному алгоритму. Причем первая точка, называемая начальным приближением, выбирается заранее. Пусть известно некоторое приближенное значение Z_n корня X * . Применяя формулу Тейлора и ограничиваясь в ней

двумя членами, имеем

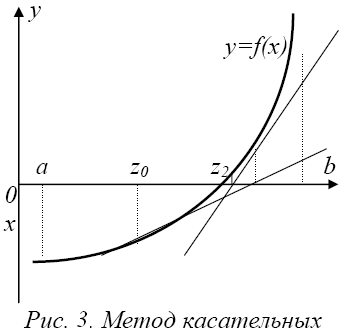Геометрическое решение этого метода заключается, как упоминалось ранее, в построении касательной к кривой y = f(x) в выбранной точке x = Z_n. Далее находится точка пересечения этой касательной с осью абсцисс, и эта точка принимается за очередное приближение к корню (рис. 3).

Решение уравнений средствами EXCEL

Видео:Численный метод Ньютона в ExcelСкачать

в примерах на EXCEL

Приближенные численные методы

Методическое пособие по дисциплине

“Приближенные методы вычислений”

Пособие предназначено для изучения дисциплины “Приближенные методы вычислений”, изучаемой на третьем году обучения для всех направлений бакалавриата, при подготовке к выполнению лабораторных работ. Оно должно дать студенту основные понятия о численных методах с использованием современных компьютеров и доступных программных средств.

Основное внимание уделено тщательно подобранным примерам, позволяющим наиболее ярко проиллюстрировать те или иные особенности каждого метода. Все примеры выполнены на одном из самых мощных современных программных средств — табличном процессоре EXCEL, входящим в состав широко распространенного пакета MICROSOFT OFFICE.

Пособие охватывает основные темы раздела учебной программы указанной дисциплины. Кроме методов, входящих в учебную программу, в пособии описаны алгоритмы и вычислительные процедуры встроенных в EXCEL специальных подпрограмм и функций, позволяющих реализовать те или иные численные методы, например, матричные вычисления, линейный регрессионный анализ, метод сопряженных градиентов, линейное программирование и т.п.

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным. 5

1.1 Отделение корней. 5

1.2 Уточнение корней: метод итераций. 6

1.3 Уточнение корней: метод Ньютона. 8

1.4. Уточнение корней: метод бисекции ( деления отрезка пополам ). 10

1.5 Уточнение коней: подпрограмма EXCEL “Подбор параметра”. 12

2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. 13

2.1. Матричный метод. 13

2.2. Метод приближенных вычислений. 15

2.3. Метод Гаусса – Зайделя. 18

3. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ. 20

3.1. Выбор начальных приближений. 20

3.2 Метод Ньютона. 21

3.3. Метод итераций. 23

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ. 25

4.1. Метод дихотомии. 25

4.2. Метод золотого сечения. 27

4.3. Встроенная подпрограмма EXCEL “Поиск решения”. 29

5. МНОГОМЕРНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ. 30

5.1. Безусловная оптимизация: метод покоординатного спуска. 30

5.2. Безусловная оптимизация: метод наискорейшего спуска. 32

5.3. Безусловная оптимизация: подпрограмма EXCEL “Поиск решения”. 35

5.4. Условная оптимизация: метод штрафных функций. 35

5.5. Условная оптимизация: подпрограмма EXCEL “Поиск решения”. 38

5.6. Условная оптимизация: линейное программирование. 39

6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 43

7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ. 48

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 51

8.1. Метод Эйлера. 51

8.2. Метод Рунге-Кутта четвертого порядка. 52

8.3. Метод прогноза и коррекции: метод Адамса. 53

9. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. 55

9.1. Задача Коши. 55

9.2. Краевая задача: метод стрельбы. 57

9.3. Краевая задача: метод прогонки. 57

10. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 60

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным.

Уравнение с одним неизвестным можно записать в каноническом виде

Решение уравнения заключается в нахождении корней, т.е. таких значений х, которые обращают уравнение в тождество. В зависимости от того, какие функции входят в уравнение, разделяют два больших класса уравнений — алгебраические и трансцендентные. Функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень. К трансцендентным функциям относятся показательная, логарифмическая, тригонометрические прямые и обратные и т.п.

Найти точные значения корней можно лишь в исключительных случаях. Как правило, используются методы приближенного вычисления корней с заданной степенью точности Е. Это означает, что если установлено, что искомый корень лежит внутри интервала [a,b], где a — левая граница, а b — правая граница интервала, и длина интервала (b-a) x -10x = 0

Для этого надо протабулировать функцию f(Х) = exp(Х) — 10*Х, записанную по правилам EXCEL, и построить ее график при изменении Х от какого-то Х_нач до Х_кон с шагом dХ. Пусть эти значения сначала будут таковы: Х_нач = 0, Х_кон = 5, dХ = 0,5. Если в этих пределах изменения Х нам не удастся отделить ни одного корня, тогда надо будет задать новые начальное и конечное значения х и, может быть, изменить шаг.

Для построения таблицы целесообразно воспользоваться специальной подпрограммой ТАБЛИЦА. Для этого на новом рабочем листе в ячейке B1 введем текст: ОТДЕЛЕНИЕ КОРНЕЙ. Затем в ячейку А2 введем текст: x, а в смежную ей ячейку В2 — текст: f(x). Далее оставим ячейку А3 пустой, но в ячейку В3 введем формулу исследуемой функции по правилам EXCEL, а именно

Затем заполним числовой ряд изменений X в строках А4:A14 от 0 до 5 с шагом 0,5.

Выделим блок ячеек А3:B14. Теперь дадим команду меню Данные- Таблица. Результаты табулирования будут помещены в блок ячеек В4:В14. Для того чтобы сделать их более наглядными, нужно отформатировать блок В4:B14 так, чтобы отрицательные числа окрашивались в красный цвет. В этом случае легко найти два смежных значения X, для которых значения функции имеют разные знаки. Их и надо принять за концы интервала отделения корней. В нашем случае таких интервалов, как видно из таблицы два — [0;0,5] и [ 3,5;4].

Далее следует построить график нашей функции, выделив блок А4:B14 и вызвав Мастер Диаграмм. В результате получим на экране диаграмму изменения f(X), из которой видны следующие интервалы отделения корней [0;1] и [3;4].

Если изменять теперь числовые значения х в блоке А4:A14 то значения функции в ячейках B4:B14и график будут изменяться автоматически.

1.2 Уточнение корней: метод итераций.

Для уточнения корня методом итераций должно быть задано:

1) уравнение f(X) = 0, причем f(X) должно быть задано в виде формулы,

2) числа a — левая граница и b — правая граница интервала, внутри которого лежит один корень,

3) число Е — заданная точность получения корня.

Сам метод можно разбить на два этапа:
а) переход от канонического вида записи уравнения f(X)=0 к итерирующему виду X = g(X),
б) вычислительная итерирующая процедура уточнения корня.

Перейти от канонического вида уравнения к итерирующему можно различными способами, важно лишь чтобы при этом выполнялось достаточное условие сходимости метода: çg’(X)ç 0 сходимость будет монотонной, т.е. с увеличением итераций D будет приближаться к Е монотонно (не меняя знака), в то время как при g’(X) 1 на интервале [a,b] и характер сходимости будет монотонный.

Запрограммируем метод итераций для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А22 внесем число, равное 0. В ячейку В22 запишем формулу =0,1*EXP(A22), а в ячейку С22 формулу =А22- В22. Таким образом 22 строка содержит данные по первой итерации. Чтобы получить в строке 23 данные по второй итерации, скопируем содержимое ячейки В22 в ячейку А23, записав в А23 формулу =В22. Далее надо скопировать формулы ячеек В22 и С22 в ячейки В23 и С23. Для получения данных всех остальных итераций надо выделить ячейки А23,В23,С23 и скопировать их содержимое в блок А24:C32. После этого следует проанализировать изменение D = Х — g(X) в столбце С, найти D 0. Достаточные условия сходимости метода заключаются в том, что первая и вторая производные исследуемой функции должны сохранять знак на интервале [a,b]. В качестве начального приближения выбирают обычно или a, или b, в зависимости от того, кто из них соответствует формуле выбора Х₀.

Метод Ньютона допускает простую геометрическую интерпретацию. Если через точку с координатами (X_i;f(X_i)) провести касательную к кривой f(X), то абсцисса точки пересечения этой касательной с осью 0Х и есть очередное приближение корня Х_i+1.

Метод Ньютона можно рассматривать как некоторую модификацию метода итераций, дающую наилучшую итерирующую функцию g(X) на каждом шаге итерации. Проведем следующие преобразования с исходным каноническим уравнением f(X)=0. Умножим левую и правую его части на некоторое число l, отличное от нуля. Затем прибавим слева и справа по Х. Тогда будем иметь

Дифференцируя g(X), получим g’(X) = 1 + l*f’(X). Из достаточного условия сходимости метода итераций çg’(X)ç 0.

Запрограммируем метод Ньютона для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А42 внесем число, равное Х₀=0. В ячейку В42 запишем формулу =EXP(A42)-10*А42, в ячейку С42 формулу =EXP(A42)-10, а в ячейку D42 формулу =А42- В42/C42. Затем в ячейку Е42 запишем формулу =А42-D42. Таким образом 42 строка содержит данные по первой итерации.

Чтобы получить в строке 43 данные по второй итерации, скопируем содержимое ячейки D42 в ячейку А43, записав в А43 формулу =D42. Далее надо скопировать формулы ячеек В42, С42, D42, E42 в ячейки В43, С43, D43, E43. Для получения данных всех остальных итераций надо выделить ячейки в 43 строке и скопировать их содержимое в блок А44:Е47. После этого следует проанализировать изменение D в столбце E, найти D k 0, то значение А53 равно С52. В противном случае оно должно быть равно А52. В ячейке В53 наоборот: если F52 0” (разумеется без кавычек!), в поле Значение_если_истина внесем С52, а в поле Значение_если_ложь — А52. Щелкнем по кнопке Закончить. Вот и все.

То же самое надо проделать с ячейкой В53. Только Логическое выражение будет “F52 -1 *В.

Таким образом, алгоритм решения системы матричным методом можно представить в виде следующей последовательности вычислительных процедур:

1) получить матрицу А -1 , обратную матрицеА;

2) получить решение системы по формуле Хс = А -1 *В;

3) вычислить новый вектор свободных членов Вс = А*Хс;

4) вычислить невязку R = B — Bc;

5) получить решение системы по формулеdXc = А -1 *R;

6) сравнить все компоненты вектора dXc по модулю с заданной погрешностью Е: если все они меньше Е, то закончить вычисления, иначе повторить вычисления с п.2, гдеХс = Xc + dXc.

Рассмотрим матричный метод решения системы с помощью EXCEL на примере.

Решить систему уравнений

EXCEL имеет следующие встроенные функции, реализующие матричные вычисления:

а) МОБР — обращение матрицы,

б) МУМНОЖ — умножение двух матриц,

в) МОПРЕД — вычисление определителя матрицы.

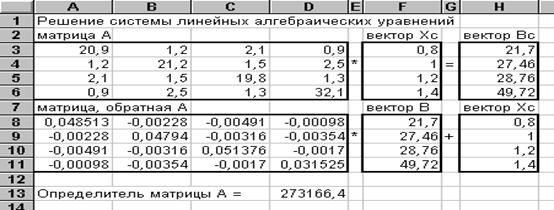
При использовании этих функций важно правильно и компактно расположить на рабочем листе блоки ячеек, соответствующие исходным и рабочим матрицам и вектор-столбцам. Откроем новый рабочий лист, щелкнув на выбранном Вами ярлычке. Отведем под матрицу А блок ячеек А3:D6. Для наглядности заключим его в черную рамку. Для этого выделим блок A3:D6, дадим команду меню Формат- Ячейки и в открывшемся диалоге выберем вкладку Рамка. Откроется новый диалог, в котором щелкнем по полю Рамка- Контур и выберем в поле Рамка- Стиль самую толстую ширину линии. Подтвердим свое решение, щелкнув на кнопке ОК. Выделим теперь блок A8:D11 под матрицу А -1 и также заключим его в черную рамку, проделав действия, аналогичные блоку матрицы А. Далее выделим блоки ячеек под вектор-столбцы (обведя их черной рамкой): блок F8:F11 — под векторВ, блок H8:H11 — под вектор Хс, получающийся в результате умножения А -1 *В, блок H3:H6 — под вектор Вс, получающийся в результате умноженияА*Хс, причем для наглядности выделим дополнительный блок F3:F6, куда скопируем компоненты вектора Хс из блока H8:H11. И наконец, занесем в ячейки Е4 и Е9 знак умножения *, а в ячейки G4 и G9 знак равенства =, затем, выделяя по очереди столбцы Е и G, дадим команду меню Формат- Столбец — Подгон ширины. Таким образом мы подготовили рабочий лист к решению нашей задачи.

Внесем исходные данные: числа матрицы А в ячейки блока A3:D6, а числа вектора свободных членовВ — в ячейки блока F8:F11.

Начнем выполнение алгоритма с обращения матрицы А. Для этого выделим блок А8:D11, куда должен быть помещен результат операции. Этот блок окрасится в черный цвет, за исключением ячейки А8. Щелкнем по кнопке f_x на панели Стандартная, осуществив вызов Мастера Функций. Откроется диалог, в котором из поля Категория функций выберем строку Мат. и тригонометрия, а из поля Имя функции — строку МОБР. Перейдем ко второму шагу диалога, щелкнув по кнопке Шаг>. Здесь в поле Массив надо набить с клавиатуры А3:D6, что соответствует блоку ячеек, занятому матрицей А. Щелкнув на кнопке Закончить, можно увидеть, что в блоке А8:D11 заполнена лишь ячейка А8. Для завершения операции обращения EXCEL требует выполнения еще двух действий. Сначала надо сделать активной строку формул, щелкнув по ней ( в любом месте строки!) — курсор мыши примет при этом форму I. Проверкой правильности Ваших действий будет появление слева от строки формул четырех кнопок, в том числе с зеленой галочкой. После этого следует нажать на клавиатуре клавишу “Ctrl”, затем не отпуская ее — клавишу “Shift”, и не отпуская и ее — клавишу “Enter”, т.е. в результате должны быть нажаты все три клавиши одновременно! Вот теперь весь блок А8:D11 будет заполнен числами и можно выделить блок H8:H11, чтобы начать операцию умножения А -1 *В.

Выделив этот блок, снова вызовите Мастер функций и в поле Имя функции — выбирайте функцию МУМНОЖ. Щелкнув по кнопке Шаг>, перейдем ко второму шагу диалога, где в поле Массив1 внесем адрес А8:D11, а в поле Массив2 — адрес F8:F11. Щелкнем по кнопке Закончить и обнаружим, что в блоке Н8:H11 заполнена лишь ячейка Н8. Активизируем строку формул ( должна появиться зеленая галочка!) и по методике, описанной выше, нажмем одновременно три клавиши “Ctrl”-”Shift”-”Enter”. Результат умножения появится в блоке Н8:H11.

Для проверки точности полученного решения системы, проведем операцию вычисленияВс=А*Хс. С этой целью скопируем только числовые значения ( а не формулы!) ячеек из блока H8:H11 в ячейки F3:F6. Сделать это надо следующим образом. Выделим блок H8:H11. Дадим команду меню Правка— Копировать. Выделим блок F3:F6. Дадим команду меню Правка— Специальная вставка. Откроется диалог, в котором в поле Вставить следует выбрать режим Значения. Подтвердим свое решение, щелкнув по кнопке ОК.

После этой операции заполнены числами блоки А3:D6 и F3:F6. Можно приступить к умножению матрицы А на вектор Хс. Для этого надо выделить блок Н3:H6, вызвать Мастер Функций и, действуя так же, как и при вычислении Хс=А -1 *В, получить Вс. Как видно из таблицы, числовые значения векторов В и Вс совпадают, что говорит о хорошей точности вычислений, т.е. невязка в нашем примере равна нулю.

Подтвердим хорошую обусловленность матрицы А вычислением ее определителя. Для этого сделаем активной ячейку D13. С помощью Мастера Функций вызовем функцию МОПРЕД. В поле массив занесем адрес блока А3:D6. Щелкнув по кнопке Закончить, получим в ячейке D13 числовое значение определителя матрицы А. Как видно, оно значительно больше нуля, что говорит о хорошей обусловленности матрицы.

2.2. Метод приближенных вычислений.

Одним из наиболее распространенных итерационных методов решения систем линейных алгебраических уравнений, отличающийся простотой и легкостью программирования, является метод приближенных вычислений или метод Якоби.

Пусть надо решить систему

Предположим, что диагональные элементы a_11, a_22, a₃₃ отличны от нуля. В противном случае можно переставить уравнения. Выразим переменные из первого, второго и третьего уравнений соответственно. Тогда

Зададим начальные приближения неизвестных

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

На этом заканчивается первая итерация. Далее, используя вычисленные значения x₁ (1) , x₂ (1) и x₃ (1) , можно провести следующую итерацию, чтобы найти x₁ (2) ,x₂ (2) и x₃ (2) , Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i (k) не станут близкими к x_i (k-1) . Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

Очевидно, что достаточные условия сходимости метода выполняются. Откроем новый рабочий лист EXCEL. Внеся в ячейку А1 текст с названием метода, отведем вторую строку для заголовка таблицы

Следующая третья строка должна содержать информацию о нулевой итерации, т.е. в ячейку А3 занесем ноль, а в ячейки В3, С3, D3 и E3 – начальные приближения, равные значениям свободных членов уравнения.

Четвертая строка будет содержать формулы для вычисления первой итерации

Для проведения остальных итераций следует скопировать формулы ячеек B4:J4 в нижние строки с 5 по, например, 15. Если числовые значения в столбце J будут меньше Е, решение найдено. В противном случае следует продолжить копирование. Результат решения показан на рисунке.

2.3. Метод Гаусса – Зайделя.

Этот метод является модификацией метода приближенных вычислений и отличается от него формулами вычислений первого и последующего приближений.

Пусть надо решить систему

Предположим, что диагональные элементы a_11, a_22, a₃₃ отличны от нуля. В противном случае можно переставить уравнения. Выразим переменные из первого, второго и третьего уравнений соответственно. Тогда

Зададим начальные приближения неизвестных

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

На этом заканчивается первая итерация. В отличии от метода Якоби, здесь использовались не только начальные приближения, но и уже вычисленные значения неизвестных на первой итерации. Далее, используя вычисленные значения x₁ (1) , x₂ (1) и x₃ (1) , можно провести следующую итерацию, чтобы найти x₁ (2) ,x₂ (2) и x₃ (2) , Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i (k) не станут близкими к x_i (k-1) . Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

Подберем начальные приближения. Выберем х_нач = 0, х_кон = 1, dx = 0,2. Откроем новый рабочий лист EXCEL и занесем эти значения х₁ в блок А4:A9. Выделим блок В4:В9 под значения х₂ первой серии, для которой f₁(x₁,x₂) = 0, и блок С4:С9 — под значения х₂ второй серии, для которой f₂(x₁,x₂) = 0. Блок D4:D9 отведем для функции f₁(x₁,x₂), а блок Е4:Е9 — для функции f₂(x₁,x₂) . Сделаем текущей ячейку D4. В нее запишем формулу =А4^3+B4^3-6*A4+3. В ячейку Е4 запишем формулу =A4^3-C4^3-6*C4+2. Теперь выделим блок D4:E4 и скопируем эти формулы в блок ячеек D5:E9. Разумеется, адреса ячеек столбцов А и С в них будут автоматически изменены.

Перейдем к заполнению блока В4:В9. Снова сделаем текущей ячейку D4. Дадим команду меню Сервис- Подбор параметра. В открывшемся диалоге в поле Установить в ячейке должен быть указан адрес ячейки D4 в абсолютных адресах. В поле Значение следует занести ноль, а в поле Изменяя ячейку — занести адрес ячейки В4 ( можно в относительных адресах). Щелкнем по кнопке ОК. Появится новый диалог Состояние подбора параметра. Если решение найдено, то, щелкнув по кнопке ОК, получим в ячейке B4 нужное нам числовое значение. Далее эту процедуру надо повторить для всех ячеек блока D4:D9. В результате будет заполнен блок В4:В9.

Аналогичным образом следует заполнить блок С4:С9, используя блок Е4:Е9.

Если блоки в столбцах В и С заполнены, можно построить диаграмму. Для этого необходимо выделить блок А3:Е9. Затем щелкнуть по кнопке Мастер Диаграмм на панели Стандартная. Передвигаясь по диалогу с помощью кнопки Шаг>, выполнить все 5 шагов построения диаграммы, причем на Шаге 2 из 5 выбрать тип XY-точечная, а на Шаге 3 из 5 — формат 6. Анализируя построенную диаграмму, можно сделать вывод о том, что в качестве начальных приближений можно выбрать х1 =0,5 и х2 = 0,5.

3.2 Метод Ньютона.

Пусть задана система нелинейных уравнений 2-го порядка

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е — точность вычислений значений корней. Функции должны быть дифференцируемы и формулы частных производных тоже должны быть известны.

Исходную систему можно записать в матричном виде

где X — двумерный вектор- столбец с компонентами < x₁,x₂ >, а F — двумерный вектор- функция. Метод Ньютона — это метод последовательных приближений по формуле

i — номер итерации, ( i = 0,1,2. )

J_i -1 — матрица, обратная матрице J на i-той итерации,

J— матрица Якоби, т.е. матрица первых частных производных:

Таким образом на каждой итерации вычисляется вектор Р, его компоненты сравниваются с заданной погрешностью Е по формуле

Для решения задачи воспользуемся встроенными в EXCEL матричными функциями и процедурами так, как это сделано в разделе 2 настоящего пособия при решении систем линейных уравнений.

Проведем вычисления на том же рабочем листе, что и в примере 3.1. Необходимо отвести блоки ячеек для векторов Х,F и P, для матриц J иJ -1 , а также ячейки для вычисления якобиана и текущей величины погрешности D. Затем занести начальные приближения в блок Х и формулы в блокиJ иF. Далее с помощью Мастера функций надо организовать вычисление якобиана функцией МОПРЕД , матрицы J -1 — функцией МОБР и вектора Р — функцией МУМНОЖ по аналогии с примером 2.1. В результате будет выполнена первая итерация метода Ньютона и по численному значению D следует принять решение о проведении дальнейших итераций.

Из таблицы ясно, что D>E и дальнейшие итерации необходимы. По формуле Ньютона для получения новых числовых значений вектора Х нужно из значений блока Хвычесть значения блока Р. Это можно выполнить таким образом. Выделим блок Ри дадим команду меню Правка- Копировать. Затем выделим блок Хи дадим команду меню Правка- Специальная вставка. В появившемся диалоге выберем в поле Вставить переключатель Значения, а в поле Операция — переключатель Вычесть и подтвердим свой выбор щелчком по кнопке ОК. В результате будет выполнена вторая итерация. Блок ячеек Р будет обрамлен бегущей пунктирной линией. Если значение D получится все еще большим чем Е, то следует снова выделить блок Х и повторить команду меню Правка- Специальная вставка с указанием тех же переключателей. Эти манипуляции можно проводить до тех пор, пока D не станет меньше, чем Е. Во время проведения итераций нужно визуально контролировать числовое значение якобиана для выполнения достаточных условий сходимости метода.

3.3. Метод итераций.

Пусть задана система нелинейных уравнений 2-го порядка

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е — точность вычислений значений корней.

Для применения итераций исходная система приводится к виду

где функции g_i называются итерирующими. Алгоритм решения задается итерирующими формулами

где i -номер итерации, i = 0,1,2. Для прекращения итераций вычисляются значения

и D сравнивается с Е. Итерации продолжаются до тех пор, пока не выполнится условие D 3 + x₂ 3 + 3)/6

При изменении независимых переменных в пределах 0 2 )/2 + (x₂ 2 )/2,

Проведем вычисления на том же рабочем листе, что и в примере 4.2.

Отведем столбец А, начиная с 26 строки под значения х₁, столбец В под значения х₂, столбец С — под g₁, столбец D — под g₂, следующие три столбца под р₁,р₂ и D.

В строке 27 сформируем формулы для второй итерации, а затем скопируем их в блок А28:G32, с учетом изменений относительных адресов ячеек. В результате будем иметь заполненную таблицу

Как видно, процесс итераций сходится достаточно быстро.

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Одномерная задача оптимизации в общем случае формулируется следующим образом: найти значение независимой переменной Х, заданной на интервале[a,b], при котором некоторая целевая функция f(X) принимает минимальное значение. Если ставится задача нахождения максимума, например, функции g(X), то преобразованием f(X) = — g(X) она приводится к отысканию минимума f(X). Целевая функция f(X) должна быть задана в виде формулы. Если существует производная f’(X), то задача сводится к решению уравнения f’(X) = 0, например, методами, описанными в разделе 2.

Численные методы оптимизации используются тогда, когда целевая функция недифференцируема и, в общем случае, может быть не гладкой и даже непрерывной, т.е. может иметь разрывы первого рода по Дирихле.

Единственное условие, предъявляемое к целевой функции — она должна быть унимодальной на интервале [a,b], т.е. иметь на этом интервале только один минимум и не иметь ни максимумов, ни точек перегиба. Математически свойство унимодальности записывается так. Функция f(X) называется унимодальной на интервале [a,b], если на этом интервале существует такая точка Х*, что для значений Х

Итерации прекращаются, если d f(X₂), то а= X₁, иначе b= X₂,

4) если длина нового интервала d=(b-a)

Дата добавления: 2015-02-10 ; просмотров: 92 ; Нарушение авторских прав

💥 Видео

Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение системы уравнений в ExcelСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Решение системы уравнения с помощью настройки поиск решенияСкачать

Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

Никогда не делай этих действий в военкомате 2024. Как не пойти в армию законно 2024Скачать

Решение системы неравенств с двумя переменными. 9 класс.Скачать

Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

12 Метод Ньютона (Метод касательных) Excel Calc Численные методы решения нелинейного уравненияСкачать

Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Метод_Зейделя_ExcelСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать