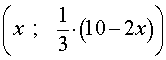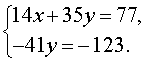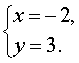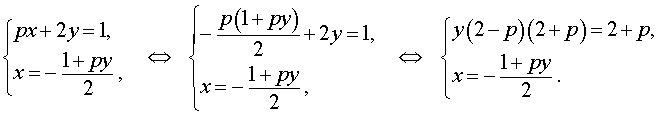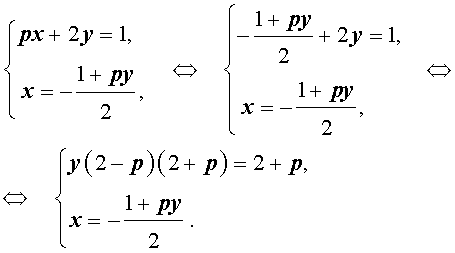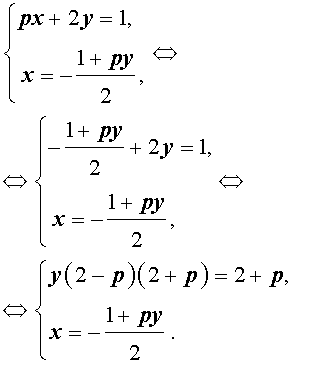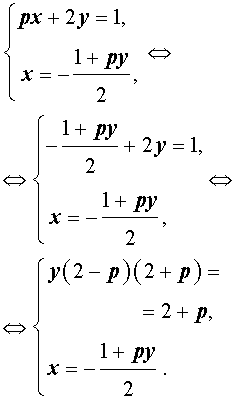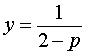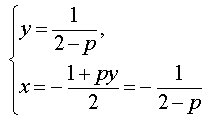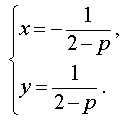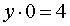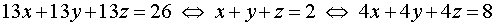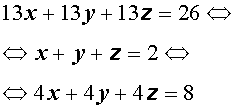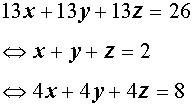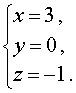- Если несколько линейных уравнений с одними теми же неизвестными рассматривают совместно, то говорят, что это система линейных уравнений с несколькими неизвестными.
- Решить систему с двумя неизвестными – это значит найти все пары значений переменных, которые удовлетворяют каждому из заданных уравнений. Каждая такая пара называется решением системы.
- Как решить систему линейных уравнений?
- Система линейных уравнений с тремя переменными
- Линейное уравнение с тремя переменными и его решение
- Решение системы линейных уравнений с тремя переменными методом подстановки
- Решение системы линейных уравнений с тремя переменными методом Крамера
- Примеры
- Системы линейных уравнений
- Линейные уравнения (уравнения первой степени) с двумя неизвестными
- Системы из двух линейных уравнений с двумя неизвестными
- Системы из трех линейных уравнений с тремя неизвестными
- 🌟 Видео
Если несколько линейных уравнений с одними теми же неизвестными рассматривают совместно, то говорят, что это система линейных уравнений с несколькими неизвестными.
Решить систему с двумя неизвестными – это значит найти все пары значений переменных, которые удовлетворяют каждому из заданных уравнений. Каждая такая пара называется решением системы.
Пример:
Пара значений (x=3);(y=-1) является решением первой системы, потому что при подстановке этих тройки и минус единицы в вместо (x) и (y), оба уравнения превратятся в верные равенства (begin3-2cdot (-1)=5 \3 cdot 3+2 cdot (-1)=7 end)
А вот (x=1); (y=-2) — не является решением первой системы, потому что после подстановки второе уравнение «не сходится» (begin1-2cdot(-2)=5 \3cdot1+2cdot(-2)≠7 end)
Отметим, что такие пары часто записывают короче: вместо «(x=3); (y=-1)» пишут так: ((3;-1)).
Видео:Система линейных уравнений с тремя переменными | Алгебра 7 класс #49 | ИнфоурокСкачать

Как решить систему линейных уравнений?
Есть три основных способа решения систем линейных уравнений:
Возьмите любое из уравнений системы и выразите из него любую переменную.
Полученное выражение подставьте вместо этой переменной в другое линейное уравнение системы.
Ответ запишите парой чисел ((x_0;y_0))
Замечание к шагу 1: нет никакой разницы какую переменную и из какого уравнения выражать. Обычно более удобно выражать ту переменную, перед которой нет коэффициента или, говоря точнее, коэффициент которой равен единице (в примере выше это был икс в первом уравнении).
Почему так? Потому что во всех остальных случаях у нас при выражении переменной получилась бы дробное выражение . Попробуем, например, выразить икс из второго уравнения системы:
И сейчас нам нужно будет эту дробь подставлять в первое уравнение и решать то, что получиться. До верного ответа мы бы всё равно дошли, но идти было бы неудобнее
Способ алгебраического сложения.
Равносильно преобразовывая каждое уравнение в отдельности, запишите систему в виде:(begina_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end).
Теперь нужно сделать так, чтоб коэффициенты при одном из неизвестных стали одинаковы (например, ((3) и (3)) или противоположны по значению (например, (5) и (-5)). В нашем примере уравняем коэффициенты при игреках. Для этого первое уравнение домножим на (2), а второе — на (3).
(begin2x+3y=13 |cdot 2\ 5x+2y=5 |cdot 3end)(Leftrightarrow)(begin4x+6y=26\15x+6y=15end)(Leftrightarrow)
Сложите (или вычтите) почленно обе части уравнения так, чтобы получилось уравнение с одним неизвестным.
Найдите неизвестное из полученного уравнения.
Подставьте найденное значение неизвестного в любое из исходных уравнений и найдите второе неизвестное.
Ответ запишите парой чисел ((x_0;y_0)).
Замечание к шагу 3: В каком случае уравнения складывают, а в каком вычитают? Ответ прост – делайте так, чтоб пропала переменная: если «уравненные» коэффициенты имеют один и тот же знак – вычитайте, а если разные – складывайте.
Пример. Решите систему уравнений: (begin12x-7y=2\5y=4x-6end)
Приводим систему к виду (begina_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end) преобразовывая второе уравнение.
«Уравняем» коэффициенты при иксах. Для этого домножим второе уравнение на (3).
Знаки при иксах разные, поэтому чтоб иксы пропали, уравнения надо сложить.
Делим уравнение на (8), чтобы найти (y).
Игрек нашли. Теперь найдем (x), подставив вместо игрека (-2) в любое из уравнений системы.
Икс тоже найден. Пишем ответ.
Приведите каждое уравнение к виду линейной функции (y=kx+b).
Постройте графики этих функций. Как? Можете прочитать здесь .
Ответ: ((4;2))
Матхак. Если сомневаетесь в правильности ответа (неважно каким способом вы решали), проверьте подстановкой значений (x_0) и (y_0) в каждое уравнение. Если оба уравнения превратятся в верные равенства, то ответ правильный.
Пример: решая систему (begin3x-8=2y\x+y=6end), мы получили ответ ((4;2)). Проверим его, подставив вместо икса (4), а вместо игрека (2).
Оба уравнения сошлись, решение системы найдено верно.
Пример. Решите систему уравнений: (begin3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end)
Перенесем все выражения с буквами в одну сторону, а числа в другую.
Во втором уравнении каждое слагаемое — четное, поэтому упрощаем уравнение, деля его на (2).
Эту систему линейных уравнений можно решить любым из способов, но мне кажется, что способ подстановки здесь удобнее всего. Выразим y из второго уравнения.
Подставим (6x-13) вместо (y) в первое уравнение.
Первое уравнение превратилась в обычное линейное . Решаем его.
Сначала раскроем скобки.
Перенесем (117) вправо и приведем подобные слагаемые.
Поделим обе части первого уравнения на (67).
Ура, мы нашли (x)! Подставим его значение во второе уравнение и найдем (y).
Видео:Система с тремя переменнымиСкачать

Система линейных уравнений с тремя переменными
Линейное уравнение с тремя переменными и его решение
Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.
Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac x-8y-5z = 7$
Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.
Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$
Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.
О тождествах – см. §3 данного справочника
Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.
Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .
Решение системы линейных уравнений с тремя переменными методом подстановки
Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)
Например: решить систему
$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$
Решение системы линейных уравнений с тремя переменными методом Крамера
Для системы с 3-мя переменными действуем по аналогии.
Дана система 3-х линейных уравнений с 3-мя переменными:
$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$
Определим главный определитель системы:
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$
и вспомогательные определители :
$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$
Тогда решение системы:
Соотношение значений определителей, расположения плоскостей и количества решений:
Три плоскости пересекаются в одной точке
Три плоскости параллельны
Две или три плоскости совпадают или пересекаются по прямой
Бесконечное множество решений
Осталось определить правило вычисления определителя 3-го порядка.
Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end — b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$
$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$
Примеры
Пример 1. Найдите решение системы уравнений методом подстановки:
$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$
$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac = 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$
$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$
Пример 2. Найдите решение системы уравнений методом Крамера:
$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin -2 & 3 \ 9 & -1 \ end — 1 = begin -2 & -1 \ 9 & 2 \ end = $$
$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end — 13 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -2 \ 1 & 9 \ end = $$
$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end — 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$
$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$
$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$
$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end — 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$
$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end — 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$
Пример 3*. Решите систему уравнений относительно x,y,и z:
$$ a neq b, b neq c, a neq c $$
Решаем методом замены:
$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$
Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$
Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:
Из второго уравнения получаем:
Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:
$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$
$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Видео:Алгебра 7 класс (Урок№48 - Решение систем двух линейных уравнений с двумя неизвестными.)Скачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
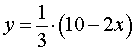 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Решение систем уравнений методом подстановкиСкачать

Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
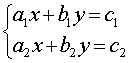 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
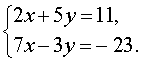 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
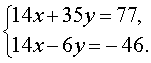 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
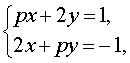 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
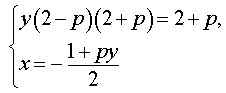 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
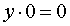
и его решением является любое число 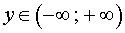
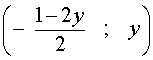
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
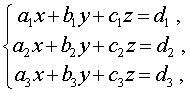 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
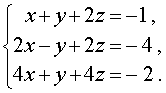 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
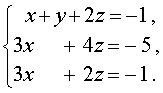 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
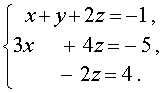 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
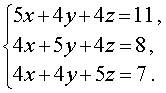 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
🌟 Видео
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Видеоурок: решение систем линейных уравнений методом подстановки с тремя неизвестными. 7 классСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Графический метод решения систем линейных уравнений 7 классСкачать

7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать

Решение систем с тремя переменными. Практическая часть. 9 класс.Скачать