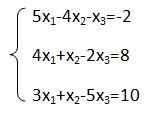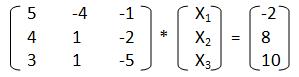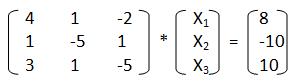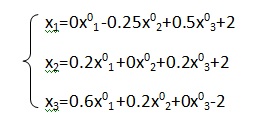В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
- Общие сведения об итерационных методах или методе простой итерации
- Метод Якоби
- Метод Зейделя
- Метод простой итерации
- Методы Зейделя и простой итерации
- Методы решения систем линейных алгебраических уравнений
- Метод простых итераций
- Готовые работы на аналогичную тему
- Метод Зейделя
- Итерационные методы решения СЛАУ. Метод простых итераций. Метод Зейделя.
- Введение
- Метод простых итераций
- Метод Зейделя
- 🎬 Видео
Видео:Метод Зейделя Пример РешенияСкачать

Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Видео:Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = — a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε
В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) — x ( n ) ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 — 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) — x ( n ) ε
Далее вычисляем нормы разности векторов:
x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Видео:Метод простой итерации Пример РешенияСкачать

Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Видео:8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x — τ ( A x — b ) , τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .
Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .
Видео:Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Методы Зейделя и простой итерации
Вы будете перенаправлены на Автор24
Методы Зейделя и простой итерации — это методы решения систем линейных алгебраических уравнений при помощи итераций.
Видео:Решение слау методом итераций. Метод простых итераций c++.Скачать

Методы решения систем линейных алгебраических уравнений
Методы решения систем линейных алгебраических уравнений подразделяются на прямые, являющиеся точными, и итерационные, которые являются приближёнными. Прямые методы базируются на исполнении не бесконечного количества арифметических действий. В качестве примера таких методов можно привести метод обратной матрицы, метод Гаусса, метод Гаусса-Жордана, метод прогонки для трех диагональных матриц и так далее. Сущность итерационных методов состоит в том, чтобы путём последовательных приближений найти решение системы с требуемой точностью. Наиболее распространёнными итерационными методами считаются метод простых итераций и метод Зейделя. Они фактически являются эквивалентными, но конечно имеют и отличия.
Данные предполагают наличие больших расчетных объемов, однако это не мешает им обладать достаточно простой структурой. Как отмечалось выше, в итерационных методах за счет предыдущих приближений могут быть получены новые приближения, и, в случае удовлетворения системой условию сходимости, эти приближения имеют всё меньше отличий от аналитического решения.
В итерационных методах обычно присутствуют следующие основные этапы:
- Приведение исходной системы вида $ ¯A * ¯x = ¯b $ к итерационной форме.
- Осуществление проверки условия сходимости.
- Реализация решения системы выбранным методом.
Видео:Метод_Зейделя_ExcelСкачать

Метод простых итераций
Для систем общего вида должно выполняться тождество m = n, где m — это число уравнений в системе, а n — это количество неизвестных.
То есть, нет смысла в решении не доопределенных (m меньше n) и переопределенных (m больше n) систем уравнений, так как их можно свести за счёт элементарных алгебраических преобразований к нормальным (m=n) системам линейных уравнений. Иначе говоря, когда присутствует «ненормальная» система уравнений, то перед началом использования метода простых итераций, следует преобразовать её в нормальную.
Готовые работы на аналогичную тему
Систему линейных уравнений можно записать в матричной форме, где:
- A является матрицей коэффициентов.
- b является вектором свободных членов.
- x является вектором неизвестных.
В качестве примера рассмотрим следующую систему:
Рисунок 1. Система уравнений. Автор24 — интернет-биржа студенческих работ
Представим её в матричной форме:
Рисунок 2. Система уравнений в матричной форме. Автор24 — интернет-биржа студенческих работ
Первый этап итерационного метода заключается в преобразовании исходной системы, то есть матрицы А и вектора b в итерационную форму, где С и d являются итерационными формами исходных данных.
Преобразование в итерационный вид может быть реализована по следующим формулам:
$c_ = -a_ / a_$ $D_i = b_i / a_$ где i, j = 1,2,3…
Необходимо заметить, что диагональные компоненты новой матрицы обнуляются, хотя должны быть равны -1. В результате для рассматриваемой системы получается:
Рисунок 3. Матрица. Автор24 — интернет-биржа студенческих работ
Если выполнять преобразование исходной системы к итерационной форме, то она не удовлетворит условию сходимости:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
То есть отдельные элементы матрицы C оказываются больше единицы. А по условию сходимости, приведённому выше, очевидно, что, если хотя бы один элемент будет больше единицы, то условие не выполнится, и решение системы путем простых итераций найти невозможно. Прежде чем осуществлять этапы итерационных методов, следует привести исходную систему к виду, в котором все диагональные компоненты будут максимальными по модулю в своих строках. Лишь при этом виде матрицы коэффициентов будет выполняться условие сходимости.
Очевидно, что в рассматриваемом примере третий элемент третьей строки по модулю больше других. Его следует оставить неизменным. Необходимо поменять местами первую и вторую строки, а далее умножить строку, ставшую первой, на минус единицу и сложить её с новой второй строкой. В результате получится:
Рисунок 5. Матрица. Автор24 — интернет-биржа студенческих работ
Теперь при подстановке в формулы итерационная форма получится верной и второй этап, то есть проверка условия сходимости, может быть успешно пройден. Если же система не проходит эту проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. Если же условие сходимости исполняется, то стратегия метода простых итераций может быть применена и можно переходить к третьему этапу. В конечном счете будет получена система линейных алгебраических уравнений в итерационной форме:
Рисунок 6. Система линейных уравнений. Автор24 — интернет-биржа студенческих работ
Здесь $x_1, x_2, x_3$ являются приближениями, которые получаются на текущем шаге итерации за счет приближений, найденных на предыдущей итерации — $x^0_1, x^0_2, x^0_3$.
Итерационный процесс по методу простых итераций продолжается до тех пор, пока вектор приближений не придёт к необходимой точности, то есть, пока не исполнится условие выхода:
$Max|x_i – x^0_i|$ ∠ $ε$
Здесь ε является требуемой точностью.
Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Метод Зейделя
Как уже отмечалось выше, метод простых итераций и метод Зейделя, по своей сути, являются идентичными. Разница заключается в том, что в методе Зейделя вычисление вектора приближений на текущей итерации выполняется с применением данных, которые были получены ни только на предыдущей, но и на исполняемой итерации. Это означает, что элемент x1 определяется через x2 и x3, величины которых были рассчитаны на предыдущей итерации, а последующий элемент x2 уже рассчитывается на основании x1, найденного именно на текущей итерации, и x3, вычисленного на предыдущей. Иначе говоря, данные в методе Зейделя для определения вектора X используются в процессе расчётов по мере их вычисления. А в методе простых итераций применяются данные, которые были получены именно на предыдущей итерации.
На основании этого отличия можно сделать вывод о том, что метод Зейделя имеет лучшую сходимость в сравнении с методом простых итераций, поскольку для него характерна тенденция применения приближений, которые получаются по ходу процесса и являются наиболее близкими к конечному результату.
Ниже представлена программная реализация метода Зейделя:
Procedure Zeidel(C:array of array of real;d:array of real;n:integer);
Видео:Решение системы линейных уравнений методом итерацийСкачать

Итерационные методы решения СЛАУ. Метод простых итераций. Метод Зейделя.
Видео:Решение системы линейных уравнений методом простых итераций в MS ExcelСкачать

Введение
Методы решения систем линейных алгебраических уравнений классифицируют на прямые (точные) и итерационные. Прямые методы основаны на выполнении конечного числа арифметических операций, это, например, метод обратной матрицы, метод Гаусса, метод Гаусса-Жордана, метод прогонки для трехдиагональных матриц и т.д. Суть итерационных методов, в свою очередь, заключаются в том, чтобы за счет последовательных приближений получить решение системы, определяемое необходимой точностью. Я попытаюсь наиболее подробно рассмотреть два из них, а именно метод простых итераций и метод Зейделя. Они практически эквивалентны, поэтому ограничусь подробным анализом метода простых итераций, а в конце пару слов скажу по поводу метода Зейделя. А прежде чем приступить к рассмотрению какого-то конкретного метода, хочется немного описать итерационные методы решения СЛАУ в общем плане.
Эти методы характеризуются большими расчетными объемами, что не мешает им быть по своей структуре достаточно простыми. Всего-навсего за счет предыдущих приближений мы получаем новые приближения, и, если система удовлетворяет условию сходимости, то эти приближения все меньше и меньше отличаются от аналитического решения.
Для итерационных методов можно выделить три последовательных этапа:
- Приведение исходной системы вида
к итерационной форме
.
- Проверка условия сходимости.
- Решение системы одним из методов.
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Метод простых итераций
Теперь, опираясь на представленную последовательность, разберем метод простых итераций. Сразу условимся, что для общего вида систем выполняется тождество m=n, где m — количество уравнений в системе, n — количество неизвестных. Т.е. не имеет смысла решать недоопределенные (m n) системы, т.к. они могут быть сведены путем элементарных алгебраических преобразований к нормальным (m=n) системам линейных уравнений. Другими словами, если у вас имеется «ненормальная» система, то прежде, чем использовать метод простых итераций, преобразуйте ее к нормальной.
Все мы знаем, что система линейных уравнений может быть записана в матричной форме, где A – матрица коэффициентов, b – вектор свободных членов, x – вектор неизвестных. Возьмем систему:
Ее матричная форма:
Смотрим на первый этап итерационных методов – он предполагает преобразование исходной системы, а именно матрицы А и вектора b к итерационной форме, где С и d – итерационные формы исходных данных.
Переход к итерационному виду осуществляется по следующим формулам:
Также следует отметить, что, несмотря на эти формулы, диагональные элементы новой матрицы обнуляются, хотя должны быть равны -1.
В итоге для нашей системы должно получиться:
Проверьте. Ошибка? Если считать по исходной системе, то да. Все дело в том, что я не сказал про одно «НО».
Это «НО» заключается в следующем. Если мы будем преобразовывать исходную систему к итерационной форме, то она не удовлетворит условию сходимости:
Некоторые элементы матрицы C будут больше единицы. А глядя на условие сходимости, становится понятно, что, если хотя бы один будет больше единицы, то условие не выполнится, и решение системы путем простых итераций не будет найдено.
Поэтому открываем учебник по линейной алгебре и вспоминаем элементарные матричные преобразования! Прежде чем следовать этапам итерационных методов, нужно привести исходную систему к виду, в котором все диагональные элементы были бы максимальными по модулю в своих строках. Только при таком виде матрицы коэффициентов можно надеется на выполнение условия сходимости.
Смотрим нашу начальную систему. Видим, что третий элемент третьей строки по модулю больше других. Оставим его неизменным. Меняем местами первую и вторую строки. Теперь умножаем строку, ставшую первой, на -1 и складываем с новой второй. В итоге получаем:
Теперь при подстановке в формулы мы получим итерационную форму верно. К сожалению, это преобразование начальной системы к «благоприятному» виду — чистая аналитика, поэтому записать его в программный код очень сложно, а если даже и попытаться, то в некоторых случаях вероятно возникновение ошибок.
Переходим ко второму этапу: «Проверка условия сходимости» (формулу смотрите выше). Если система не проходит проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. В этом случае можно попытаться получить другую «благоприятную» форму. Если условие сходимости выполнено, то стратегия метода простых итераций применима и осуществляется переход к третьему этапу.
В конечном счете, мы получили систему линейных алгебраических уравнений в итерационной форме:
где x1, x2, x3 – приближения, получаемые на текущей итерации за счет приближений полученных на предыдущей итерации — x 0 1, x 0 2, x 0 3.
Итерационный процесс в методе простых итераций идет до тех пор, пока вектор приближений не достигнет заданной точности, т.е. пока не выполнится условие выхода:
Я думаю, что теории достаточно, осталось лишь обратить внимание на программную реализацию метода.
Далее представлен код, написанный в среде PascalABC.Net. Эта система была выбрана мной благодаря возможности работать с динамическими массивами (в Turbo Pascal предусмотрены только статические). Поэтому программа может решать любую нормальную систему линейных уравнений, которая проходит проверку условия сходимости. Главное, чтобы вид этой системы соответствовал вышеописанным критериям.
Применимо к нашей СЛАУ программа выдаст ответ: x1=1.0000002, x2=2.000000009, x3=-1.0000002. Такой вектор приближений соответствует точности 10 -6 , прописанной в коде.
Видео:Алгоритмы С#. Метод простых итерацийСкачать

Метод Зейделя
Как я уже говорил, метод простых итераций и метод Зейделя почти идентичны. Разница лишь в том, что в методе Зейделя расчет вектора приближений на текущей итерации происходит с использованием данных, полученных ни только на предыдущей, но и на нынешней итерации. То есть элемент x1 вычисляется на основе x2 и x3, значения которых, расчитаны на предыдущей итерации, а следующий элемент x2 уже вычисляется за счет x1, полученного именно на текущей итерации, и x3 на предыдущей. Другими словами данные в методе Зейделя для расчета вектора X поступают в процесс по мере их вычисления. А в методе простых итераций используются данные, строго полученные на предыдущей итерации.
Это различие говорит нам о том, что метод Зейделя обладает наилучшей сходимостью нежели метод простых итераций, так как для него характерна тенденция использования приближений, получаемых по ходу процесса, наиболее близких к конечному результату.
И на последок покажем это различие в практической реализации. Чтобы метод простых итераций «превратился» в метод Зейделя нужно поменять процедуру ProstIterMetode, например, на следующую:
🎬 Видео
9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Решение системы уравнений методом ГауссаСкачать

2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать

6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

Метод итерацийСкачать

Лекция 5, Итерационные методы решения систем линейных уравненийСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать







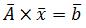 к итерационной форме
к итерационной форме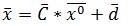 .
.