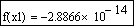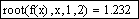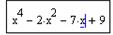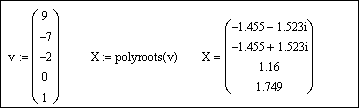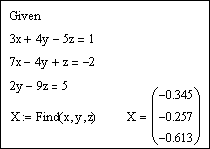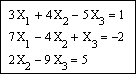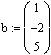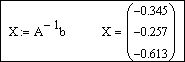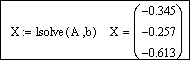Решение систем линейных уравнений методом гаусса в mathcad (3 видео)

Содержание

Решение систем линейных уравнений методом гаусса в mathcad
MathCAD — это просто! Часть 4. Системы линейных алгебраических уравнений
Решение систем линейных уравнений методом гаусса в mathcad
📸 Видео

Видео:Решение системы уравнений методом ГауссаСкачать

Решение систем линейных уравнений методом гаусса в mathcad

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

f(x) – функция левой части уравнения f(x) = 0;
x – переменная, относительно которой требуется решить уравнение;
a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

задается матрица коэффициентов при неизвестных системы A;
задается столбец свободных членов b;
вводится формула для нахождения решения системы X:=A -1 b;
выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

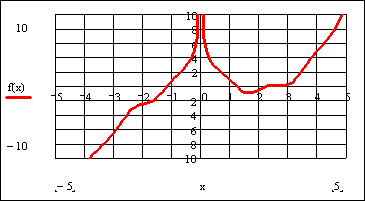
После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .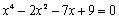

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 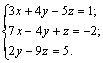Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Видео:MathCAD Решение системы линейных уравнений матричным методомСкачать

MathCAD — это просто! Часть 4. Системы линейных алгебраических уравнений

Итак, мы с вами продолжаем изучать MathCAD — самую дружелюбную к пользователю математическую среду из существующих в настоящее время. Пока мы занимались тем, что изучали способы решения уравнений — трансцендентных и алгебраических, и теперь вы знаете, как их решать с помощью MathCAD’а в общем виде или численно. Как вы могли убедиться из материала третьей части, численное решение уравнений — не такая простая задача, как может показаться с первого взгляда, однако и не такая сложная, если построить график уравнения. Но просто уравнения — это, согласитесь, довольно скучно, потому что в жизни, как правило, уравнения по одиночке не встречаются. Поэтому сегодня мы перейдем к более сложной, а значит, и более интересной, теме — попробуем решать системы уравнений. Я сказал «попробуем»? Простите, пожалуйста — я, наверное, оговорился. Конечно, не попробуем, а научимся — потому что благодаря MathCAD’у можно быть уверенным в том, что подобные попытки увенчаются успехом. Готовы? Ну что же, тогда вперед.

Решение систем с помощью функции lsolve

Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.

Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0
k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0

Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0

Здесь K — матрица (kij), составленная из коэффициентов при переменных величинах, где i — номер строки матрицы, а j — номер столбца. X и L — это, соответственно, векторы, составленные из переменных и свободных членов. Собственно, при решении СЛАУ с помощью MathCAD мы будем записывать СЛАУ именно в таком виде, потому что решение СЛАУ в MathCAD реализовано именно с помощью матричных методов. Возможно, вы что-нибудь слышали о методах решения СЛАУ Гаусса и Крамера, но даже если и нет, ничего страшного в этом нет — MathCAD тем и удобен, что с его помощью можно решать уравнения, не задумываясь над тем, каким именно алгоритмом пользуется математическая система при их решении.

Итак, для начала давайте посмотрим, каким именно образом в MathCAD’е нужно задавать матрицы. Для этого на панели инструментов Matrix нажмите кнопку Matrix or Vector, а в появившемся окне задайте количество столбцов и строк в матрице. Мы с вами попробуем решать для начала СЛАУ из четырех уравнений, и, соответственно, нам нужна будет матрица размером четыре на четыре элемента. Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать «K_:=», а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете
воспользоваться теми, которые приведены на скриншоте — с ними цифры в ответе получаются довольно ровными и красивыми), нужно для решения СЛАУ использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать:
lsolve(K_, L_) =

Ну, а после знака равенства MathCAD нам уже нарисует результат.

С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, «а». Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак «равно» в MathCAD’е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.

Решение с помощью solve

В общем-то, решать такую систему можно было бы и используя уже знакомый нам с вами оператор solve. Для этого достаточно записать уравнения в виде матрицы, а затем применить к ней оператор solve точно так же, как если бы мы с вами решали не целую систему, а всего лишь одно- единственное уравнение. «Записать уравнения в виде матрицы» в данном случае означает не запись матричного уравнения KX + L = 0, а просто запись в каждой строке одностолбцовой матрицы (т.е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу «=», а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.

Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи. Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.

Численное решение СЛАУ

Что ж, давайте теперь посмотрим, как решать СЛАУ с использованием численных методов их решения. Это тоже вовсе не так сложно, как может с самого начала показаться, поскольку MathCAD имеет в своем арсенале ряд средств и на этот случай. Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово «Given» (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово «Given» и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.

Теперь, когда вы знаете уже столько разных способов решения СЛАУ, вполне логично было бы задаться вопросом: а какой из них лучше при прочих равных условиях? В литературе, как правило, рекомендуется использовать функции lsolve или find, дающие точность до 15 знаков после запятой — однако на самом деле, учитывая тот факт, что такая точность бывает нужна не так уж часто, данным советом можно пренебречь, потому что точность решения системы намного больше зависит от нее самой, нежели от используемого метода ее решения в MathCAD’е. Так что используйте пока что смело тот, который показался вам наиболее удобным, а о погрешностях при решении СЛАУ мы с вами еще поговорим, но только, пожалуй, немного попозже.

Компьютерная газета. Статья была опубликована в номере 16 за 2008 год в рубрике soft

Видео:Решение СЛАУ в пакете MathCadСкачать

Решение систем линейных уравнений методом гаусса в mathcad

Функция submatrix(Ag, 1, 3, 4, 4), выделяя последний столбец матрицы Ag, формирует столбец решения системы x.

Функция rref(Ar) выполняет элементарные операции над строками матрицы Ar — приводит ее к ступенчатому виду с единичной матрицей в первых столбцах, т.е.выполняет прямой и обратный ход Гауссова исключения.

Прямой и обратный ход Гауссова исключения — приведение матрицы Ar к ступенчатому виду с помощью функции rref Mathcad:

Для просмотра результата введите знак равенства, используя клавишу .

Для формирования расширенной матрицы системы используйте функцию augment(A, b), которая формирует матрицу, добавляя к столбцам матрицы системы A справа матрицу правых частей b.

Сформируем расширенную матрицу системы Ar:

Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания . Затем щелкните по кнопке Matrix or Vector Toolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке Matrix or Vector окно диалога Insert Matrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.

Определим матрицу системы A и матрицу правой части b: