Решение систем линейных уравнений код (2 видео)

Метод Гаусса на Java

Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.

Содержание

Теоретические сведения
Реализация
Вывод
Решение системы линейных алгебраических уравнений методом Гаусса средствами языка программирования Visual Basic
Решение систем линейных уравнений графическим способом заключается в построении графика каждого уравнения , входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков . Координаты этой точки ( x; y ) и будут являться решением данной системы уравнений.
Visual Basic
BestProg
Разработка приложения решения системы линейных алгебраических уравнений методом Гаусса
Условие задачи
Выполнение
Рубрики
Свежие записи
🎥 Видео

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Теоретические сведения

Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.

Алгоритм можно условно разделить на два этапа:

Прямой ход
Обратный ход

В первом этапе образуются нули ниже или выше главной диагонали, за счет использования элементарных преобразований матрицы. На втором этапе находят неизвестные начиная с конца. Подробную теорию можно посмотреть по ссылке: метод Гаусса, поэтому с теорией пожалуй все. Перейдем к реализации.

Видео:Решение системы уравнений методом ГауссаСкачать

Реализация

Начнем с постановки задачи:

нам нужно создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя приемы обобщенного программирования. Система должна содержать коэффициенты производного типа от класса Number (т.е. Float, Integer, Double и т.д.)
Запрограммировать алгоритм, который получив на вход структуру данных системы образует нули ниже главной диагонали

Начнем с написания интерфейса, который должно реализовывать каждое уравнение:

Здесь все должно быть ясно, N некоторый наследник Number‘а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.

Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.

Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number‘а будет ~~сверхточный~~ класс Float (на практике лучше брать Double). Обратите внимание, что в методе addEquation(MyEquation item) используется объект класса ListIterator, позволяющий изменять элементы перебираемого списка.

Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.

Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.

Почти все. Осталось запустить это все в методе main:

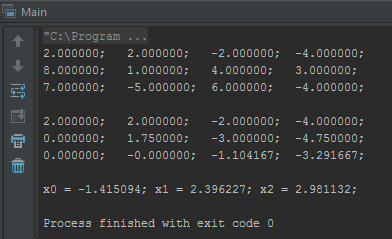
Запустим это чудо, что бы проверить корректность работы…

Это все. Исходники можно скачать на github’е.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Вывод

Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение системы линейных алгебраических уравнений методом Гаусса средствами языка программирования Visual Basic

Министерство образования и науки Республики Башкортостан

ГАОУ СПО «Стерлитамакский колледж строительства, экономики и права»

«Программирование в компьютерных системах»

по разделу 1 Объектно-ориентированное программирование

междисциплинарного курса 01.02. Прикладное программирование

Решение системы линейных алгебраических уравнений

методом Гаусса средствами языка программирования Visual Basic

3 курса, группы ПО-31

Системы линейных алгебраических уравнений

Решение систем линейных уравнений графическим способом

Список использованной литературы

Приложение А (программный код)

В курсовом проекте рассмотрена программа, реализующая приближенное решение систем линейных уравнений графическим способом, с подключением модуля “Метод Гаусса”, созданная в среде программирования Visual Basic 2010.

Системы линейных уравнений, описывают экономические процессы в обществе и производстве. Навыки решения таких систем я вляются профессионально необходимыми и демонстрируют готовность студента к профессионльной деятельности. Автоматизировать процесс решения таких систем поможет программный продукт, представленный в данном курсовом проекте. Программа написана средствами языка программирования Visual Basic , обладающего возможностями, которые помогут решить графически систему линейных уравнений, а так же реализовать метод Гаусса. Метод Гаусса выбран ак универсальный для систем линейных уравнений.

Цель курсового проекта:

Разработать код программного продукта, реализующего прибл иженно е решение систем линейных уравнений графическим способом, с подключением модуля, реализующего метод Гаусса решения систем линейных уравнений.

Задачи курсового проекта:

1. Разработать программный код модуля, реализующего прибл иженно е решение систем линейных уравнений графическим способом.

2. Выполнить отладку программного модуля «Метод Гаусса» и приближенного решения с использованием специализированных программных средств.

3. Выполнить тестирование программного модуля «Метод Гаусса» и приближенного решения по составленным тестовым заданиям.

Системы линейных алгебраических уравнений.

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Где m -количество линейных уравнений;

n -количество переменных ;

x 1 , x2, …, xn — неизвестные, которые надо определить;

Система называется однородной, если все её свободные члены равны нулю ( b 1 = b2 = … = bm = 0 ), иначе — неоднородной.

Система называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы — совокупность n чисел c 1 , c2, …, cn , таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида может иметь одно или более решений.

Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Система линейных уравнений может быть представлена в матричной форме как:

Где A — это матрица системы,

x — столбец неизвестных,

b — столбец свободных членов.

Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Эквивалентные системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

Где C — невырожденная матрица.

В частности, если сама матрица A — невырожденная, и для неё существует обратная матрица A -1 , то решение системы уравнений можно формально записать в виде

Решение систем линейных уравнений графическим способом

Решение систем линейных уравнений графическим способом заключается в построении графика каждого уравнения , входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков . Координаты этой точки ( x; y ) и будут являться решением данной системы уравнений.

Если прямые , являющиеся графиками уравнений системы, пересекаются , то система уравнений имеет единственное р ешение.

Если прямые , являющиеся графиками уравнений системы, параллельны , то система уравнений не имеет решений .

Если прямые , являющиеся графиками уравнений системы, совпадают , то система уравнений имеет бесконечное множество решений.

Примеры

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек . Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Ответ: (4; 5) .

Выражаем у через х из каждого уравнения системы, а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3).

Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В (-2; 5).

Ответ: (-2; 5).

Метод Гаусса

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Пусть исходная система выглядит следующим образом

Где A называется основной матрицей системы,

b — столбцом свободных членов.

Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj 1 ,…, x jr .

Тогда переменные xj 1 ,…, x jr называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число Bi ≠0 , где i > r ,то рассматриваемая система несовместна, т. е. у неё нет ни одного решения.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x :

Если свободным переменным системы придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему, то мы получим все решения этой СЛАУ . Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы эквивалентны, то есть множества их решений совпадают.

Разрешается:

1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений;

2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа;

3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.

С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.

Для начала избавимся от переменной x 1 во втором уравнении. Для этого из второго уравнения вычтем первое уравнение, предварительно умноженное на 3:

Переменная x 2 найдена. Осталось определить значение переменной x 1 . Для этой цели преобразуем первое уравнение, убрав из него переменную x 2 . Вычтем из первого уравнения второе уравнение, предварительно умноженное на 2. Первое уравнение станет таким:

Ответ найден. Запишем то же решение, но уже без промежуточных пояснений. Римскими цифрами I и II будем обозначать первое и, соответственно, второе уравнения.

означает, что из второго уравнения вычли утроенное первое уравнение

означает, что левую и правую части второго уравнения разделили на (-7).

Итак, решение методом Гаусса заданной СЛАУ будет иметь вид:

Обычно работают с матричной формой записи

В матричной форме записи метод Гаусса станет таким:

Видео:Решение системы уравнений методом Крамера.Скачать

Visual Basic

Visual Basic — это простой и быстрый способ создания программ для Microsoft Windows. Даже если вы не знакомы с программированием для Windows, с Visual Basic вы получите полный набор средств для упрощения разработки.

Так что же такое Visual Basic? Слово «Visual» относится к методу, используемому для создания того, что видит пользователь — графического пользовательского интерфейса , или GUI. Слово «Basic» относится к аббревиатуре BASIC (Beginners All-Purpose Symbolic Instruction Code — многоцелевой код символьных инструкций для начинающих) языка программирования, который используется программистами намного чаще, чем любой другой язык в истории вычислений. Для создания различных полезных программ достаточно изучить лишь некоторые из его возможностей.

Окно Form является вашей программы. Его можно двигать по экрану, увеличивать, уменьшать, менять его свойства в окне свойств, упорядочивать на нём объекты и в окне Code писать для него процедуры. Само окно тоже считается как объект, так сказать, «высший объект». Один из объектов всегда является «актуальным объектом», чьи свойства будут перечислены в окне свойств. Объект становится актуальным, когда на него кликнут. Узнают это чаще всего по обрамлению или по какой-нибудь другой маркировке.

Здесь всегда перчислены свойства актуального объекта (см. выше). Свойство, представленное синим, может быть изменено в строке справа. Иногда нужно вносить данные самому, иногда можно выбирать из выпадающего списка, который отображён в строке справа в виде маленькой стрелки вниз. Заметьте, что при изменении свойств окна, изменения происходят синхронно.

Здесь можно выбрать объекты, которые нужно поместить на форме. Например, чтобы нарисовать линию, кликните на символ линии. Теперь кликните на то место на форме, где должна начинаться линия и тяните мышь с нажатой кнопкой туда, где эта линия должна кончаться. Отпустите кнопку мышки. Готово! Отдельные объекты будут описаны позже.

В Basic’e процедуры начинаются с команды Sub, потом идёт имя процедуры и (). Оканчиваются процедуры командой End Sub (англ. subroutine: подпрограмма). Между этим стоят команды, принадлежащие этой процедуре. Они будут, при вызове процедуры, следовать одна за другой.

В большинстве своём процедуры — это процедуры события: для каждого события, на которое должна реагировать программа, нужно писать процедуру. Причём Sub, имя процедуры, () и End Sub будут заданы самим Basic’ом.

Процедура события Form_Load выполняется каждый раз при запуске вашего приложения прежде, чем окно появится на экране. Поэтому бесполезно уже в этой процедуре что-либо писать в окне или рисовать (например Print), т. к. это просто не будет сделанно. Окна-то ещё нет!

Событие Click происходит в том случае, если на объекте кликнуть левой кнопкой мыши. Если, к примеру, пользователь щёлкнет на одном из элементов управления, событие Click этого объекта будет тут же исполнено. Можно кликнуть по форме — для этого имеется событие Form_Click, которое может содержать различные процедуры.

Это событие происходит при двойном клике мышкой на каком-либо объекте. Внимание: ещё при первом нажатии произойдёт событие Click, но при мнгновенном втором уже нет.

Это то свойство имеется у всех объектов. Оно определяет имя объекта, под которым этот объект будет применяться в Basic-содах. Это свойство может быть изменено только в режиме design и не в самой программе. Предустановки для этого свойства — это, например, «Form1» у окна. Если где-нибудь в программе нужно обратиться к этому объекту, к примеру, если надо поменять его свойство, то надо использовать имя этого объекта.

Это свойство имеется у окон, кнопок, «этикеток» и у могих других элемнтов управления. У окон это свойство задаёт текст, который будет отображён в заголовке этого окна. Этот текст отображается также в иконке окна в таскбаре. У элементов управления это свойство определяет текст, который находится на самих элементах управления или в близи них. Это свойство может быть изменено как в режиме design, так и в ходе самой программы.

Это свойство имеется у окон и всех элементов управления, кроме таймера (он всегда «невидим»). Это свойство определяет, видим или скрыт объект, и может быть изменено, как в режиме design, так и в ходе программы. Это свойство может принимать значения только True или False.

Это свойство присутсвует у всех окон и элементов управления. Оно определяет будет ли форма или элемент управления реагировать на события произведённые пользователем. Этим свойством они будут либо включены либо выключены. Если элементы управления будут выключены они станут серыми вместо чёрных и становятся неактивными, «потушенными». Это свойство также, как и свойство Visible принимает значения только True или False

Свойства Left, Top

Эти свойства имеются у окон и почти всех элементов управления. Они определяют координаты левого верхнего угла объекта. У окон это координаты относительно экрана, а у элементов управления относительно к верхнему левому углу «внутренней» площади, т. е. окна, в котором они находятся. В режиме design эти свойства могут быть изменены при перетягивании мышкой и в окне свойств. В ходе программы эти свойства могут быть изменены тоже, но уже путём присвоения.

Свойства Width, Height

Эти свойства определяют ширину и высоту объекта. Также Вы можете изменять их как в режиме design, так и в ходе программы. Размеры объекта изменяются тогда сразу.

Командные кнопки (button) применяются чаще всего и являются простейшими элементами управления: как правило — это такие серые ящички, на которых находится текст, как например, «OK» или «Отмена», и по которым просто кликают.

Таймер назван так правильно: он никакой не настоящий элемент управления и на окне невидим, если программа запущена. Всё, что он делает — это в через определённые отрезки времени выполняет какое-нибудь событие, событие Timer’a. Много таймеров применять не надо, т. к. в Windows’e постоянно имеется максимум 16 таймеров одновременно.

Текстовое поле и поле надписи

В текстовомм поле пользователь должен вводить текст, который потом может быть использован в программе, например его имя или очки игры. На экране видно ящичек, в котором, если на него кликнуть, появится курсор. Поле надписи (этикетка, Label) используется, чтобы показывать текст, который пользователь не может изменить.

Графическое поле отображает графику, которая была сохранена, как. bmp или. ico файл. При этом будет показана только часть картинки. которая, которая поместилась в размеры графического поля. Если написать процедуру для события Click, можно использовать графическое поле, как красивую кнопку.

Программа реализующаяриближенное решение систем линейных уравнений графическим способом, с подключением модуля “Метод Гаусса”.

Программаное обеспечение необходимое для функционирования программы:

Microsoft Visual Studio 2010

Windows Xp , Windows Vista , Windows 7

Visual Basic 2010.

Программа создана для решения систем линейных алгебраических уравнений графическим способом, а так же методом Гаусса.

Программа вычисляет корни одновременно только 2 уравнений, методом Гаусса, а так же графическим способом.

Описание логической структуры:

Технология визуального программирования. Визуальная технология программирования позволяет программисту легко и быстро легко и быстро строить нагшлядный графический интерфейс для своих программ на основе стандартного набора шаблонов, графически отображаемых на экране объектов.

Структура программы с описанием функций составных частей и связи между ними:

Этот блок программы отвечает за построение системы координат на форме. Первые 2 цикла это разметка по оси Х и по оси Y . Следующие 4 строки, это оси X и Y . И наконец оставшиеся 2 цикла это Засечки по осям координат.

Этот блок отвечает за ввод данных.

Решение поставленной задачи. Первые 4 строки нужны для построения прямых на графике. Остальное, это решение методом Гаусса.

Вывод корней, полученных методом Гаусса.

Построение прямых на графике.

Связи программы с другими программами:

Связи программы с другими программами отсутствуют.

Используемые технические характеристики:

Оперативная память: 2Гб;

Процессор: Intel Pentium 4, 3.00 Ггц;

Тип системы: 32 разрядная ОС;

Вызов и загрузка:

Запуск программы происходит через редактор Visual Studio 2010.

В пункте “Файл” нажимаем на “Открыть проект”, далее на жестком диске находим папку с названием SLAU , в ней находим файл SLAU . vbproj . Кликаем на него, после чего запускается программа.

В левом верхнем углу программы, есть несколько текстовых полей, под строкой “Введите коэффициенты при x ”. В эти текстовые поля нужно ввести коэффициенты при переменных, а так же свободные члены.

После нажатия на кнопку “Построить график”, в правом верхнем углу будет построен график. На это графике будут построены 2 прямые, точка пересечения которых и будет являться примерным решением системы линейных алгебраических уравнений, которые вы ввели в правом углу.

Внизу написаны 2 переменные x 1 и x 2, а так же их значения. Эти переменные были найдены с помощью метода Гаусса, и являются точным решением системы линейных алгебраических уравнений.

После нажмите на кнопку “Построить график”.

Рис3. Выполненная программа.

В ходе курсового проекта рассмотрен метод решения систем линейных уравнений графическим способом, а так же метод Гаусса решения систем линейных уравнений. Для достижения этой цели выполнена систематизация знаний и умений по теме «Решение систем линейных уравнений», применение графики в Visual Basic 2010. Язык программирования Visual Basic отлично подошел для выполнения данного проекта, так как среда разработки языка Visual Basic , включает в себя инструменты для визуального построения интерфейса.

Были выполнены все задачи, а именно:

Построение кода модуля с заданной функциональностью; отладка программных модулей с использованием специализированных программных средств; выполнено тестирование готовых программных модулей и составил отчетную документацию с использованием информационно-коммуникационные технологий.

В ходе работы над курсовым проектом я научился работать с графикой в Visual Basic , применил свои знания в области решения систем линейных уравнений графическим способом, а так же с помощью метода Гаусса.

Список использованной литературы

http://ru. wikipedia. org

http://www. /index. php? option=com_content&view=article&id=58:&catid=19&Itemid=50

Public Class Form1

Dim Graph1 As Graphics

Dim Pen1 As New Pen ( Color .Black, 2)

Dim Pen2 As New Pen ( Color .Black, 1)

Dim brush1 As New SolidBrush ( Color .Black)

Dim font1 As New Font ( «times new roman» , 7)

Dim X, Y, a1, a2, b1, b2, c1, c2, k1, k2, m1, m2, d, z1, z2, x1, y1 As Single

Private Sub Form1_Load( ByVal sender As System. Object , ByVal e As System. EventArgs ) Handles MyBase .Load

Label1.Text = «Введите коэфициенты при х»

Button1.Text = » Построить граффик «

Private Sub Button1_Click( ByVal sender As System. Object , ByVal e As System. EventArgs ) Handles Button1.Click

Graph1 = Me .PictureBox1.CreateGraphics()

For X = -15 To 15 Step 3

Graph1.DrawString(X, font1, brush1, X * 10 + 150, 150)

For Y = -15 To 150 Step 3

Graph1.DrawString(Y, font1, brush1, 150, 150 — Y * 10)

Видео:Метод Гаусса решения систем линейных уравненийСкачать

BestProg

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Разработка приложения решения системы линейных алгебраических уравнений методом Гаусса

Условие задачи

Задана система линейных алгебраических уравнений:

Разработать приложение, которое осуществляет решение системы линейных алгебраических уравнений с помощью метода Гаусса. Работа приложения должна быть реализована в виде мастера, в котором информация для каждого следующего шага определяется из информации на предшествующем шаге.

Выполнение

При сохранении проекта имя модуля главной формы приложения оставляем по умолчанию « Unit1.cpp «.

Рис. 1. Форма приложения с созданными файлами

2. Разработка главной формы приложения

2.1. Название приложения

Задать название приложения. Для этого свойство Caption главной формы устанавливаем в значение «Метод Гаусса».

2.2. Установка свойств формы

Выделить форму. В Object Inspector установить значение следующих свойств:
– свойство Border Style = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font выбрать параметры шрифта: шрифт Tahoma , размер шрифта 12 (рис. 2).

Рис. 2. Установка параметров шрифта главной формы приложения

В результате, форма приложения примет вид как показано на рисунке 3.

Рис. 3. Главная форма приложения

2.3. Компонент типа TGroupBox

Размещаем на форме компонент (элемент управления) типа TGroupBox из палитры компонент « Tool Palette «.

Рис. 4. Компонент типа TGroupBox

В результате, система создаст объект-переменную с именем GroupBox1 .

Изменяем размеры компонента GroupBox1 на всю ширину окна главной формы.

Свойство Caption компонента GroupBox1 устанавливаем в значение « Условие задачи «. Форма приложения будет иметь вид, как показано на рисунке 5.

Рис. 5. Форма приложения после размещения компонента TGroupBox

2.4. Компонент типа TLabel .

Размещаем компонент типа TLabel в области компонента TGroupBox . Автоматически создается объект-переменная с именем Label1 (рис. 6).

Устанавливаем свойство WordWrap компонента Label1 в значение « true » (рис. 6).

С помощью мышки изменяем ширину вывода текста компонента Label1 (рис. 6).

Рис. 6. Компонент Label1 , свойство WordWrap

Свойство Caption компонента Label1 устанавливаем в значение:

Решить систему линейных алгебраических уравнений методом Гаусса

В результате, форма приложения примет вид, как показано на рисунке 7.

Рис. 7. Форма приложения после размещения компонента Label1

2.5. Компоненты типа TButton .

Размещаем на форме компоненты типа TButton . В результате образуются два объекта-переменные с именами Button1 и Button2 .

Для лучшей наглядности изменяем размеры компонент так как показано на рисунке 8.

Рис. 8. Форма приложения с размещенными компонентами Button1 и Button2

Устанавливаем такие свойства компонент Button1 и Button2:
– в компоненте Button1 свойство Caption = «Выход» ;
– в компоненте Button2 свойство Caption = «Расчет >>» .

В результате форма приложения примет вид, как показано на рисунке 9.

Рис. 9. Главная форма приложения после размещения всех компонент

3. Программирование события клика на кнопке «Выход».

Вызовем событие OnClick компонента Button1 (кнопка « Выход «) (рис. 10). Событие размещается на вкладыше Events в Object Inspector .

Процесс программирования события OnClick подробно описан здесь.

Рис. 10. Вызов события OnClick компонента Button1

В результате, откроется окно с программным кодом метода обработки события. Между скобками вводим вызов метода Close() .

Метод Close() закрывает окно главной формы приложения и осуществляет все необходимые операции по освобождению памяти, ресурсов и т.д.

Листинг метода обработки события следующий:

4. Разработка формы ввода числа уравнений n.

4.1. Размещение компонент на форме и их настройка.

Процесс создания новой формы подробно описан здесь.

Для создания новой формы вызовем команду

В результате, будет создана новая форма, как показано на рисунке 11. Сохраняем форму под именем « Unit2.cpp «.

Создаются файлы, которые соответствуют форме:
– файл « Unit2.h «, содержащий описания глобальных переменных и подключения других модулей;
– файл « Unit2.cpp «, содержащий реализацию методов формы;
– файл « Unit2.dfm «, содержащий описание изображения формы на экране (размеры окна, координаты формы относительно окна экрана, значение цветов и прочее).

Новосозданной форме отвечает объект с именем Form2 . С помощью этого имени можно приступаться к свойствам и методам формы Form2 .

Рис. 11. Новосозданная форма Form2

Осуществим настройку формы Form2 .

Сначала настроим свойства формы:
– свойство Caption = «Задайте число уравнений» ;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать следдующие параметры шрифта: шрифт Tahoma, размер шрифта 12.

Размещаем на форме такие компоненты:
– компонент типа TGroupBox которому будет отвечать объект GroupBox1;
– компонент типа TLabel, размещается внутри области компонента GroupBox1 . Компоненту типа TLabel отвечает объект-переменная Label1 ;
– компонент типа TEdit , размещается внутри области компонента GroupBox1 . Этому компоненту отвечает объект (переменная) Edit1 ;
– два компонента типа TButton , которым отвечают объекты с именами Button1 и Button2 .

Осуществим настройку свойств компонент:
– в компоненте GroupBox1 значение свойства Caption = «» (пустая строка);
– в компоненте Label1 значение свойства Caption = «n = « ;
– в компоненте Edit1 значение свойства Text = «» ;
– в компоненте Button1 значение свойства Caption = « ;
– в компоненте Button2 значение свойства Caption = «Далее >>» .

После размещения компонент и корректирования размеров формы, форма Form2 имеет вид как показано на рисунке 12.

Рис. 12. Форма Form2 после размещения и настройки всех компонент

4.2. Программирование обработчиков событий формы Form2 .

В форме Form2 программируем два обработчика событий:
– обработчик события OnClick клика на кнопке « «;
– обработчик события OnClick клика на кнопке « Далее >> «.

Листинг обработчика события клика на кнопке Button1 (« «):

Листинг обработчика события клика на кнопке Button2 (« Продолжить >> «):

Глобальная переменная ModalResult отвечает за состояние формы. Если глобальная переменная ModalResult=0 , то это означает что форма открытая как модальное окно. Как только значение ModalResult станет ненулевым, то форма Form2 закроется с кодом возврата, помещенным в ModalResult .

Таким образом, если пользователь сделает клик на кнопке Button1 , то форма Form2 закроется с кодом возврата mrNo. Если пользователь сделает клик на кнопке Button2, то форма Form2 закроется с кодом возврата mrOk .

5. Построение формы ввода коэффициентов в уравнениях.

5.1. Размещение компонент на форме и их настройка.

Создание формы происходит стандартным путем и описано в п. 4.

Сохраняем форму под именем предлагаемым по умолчанию « Unit3.cpp «.

После создания формы получим объект с именем Form3 . С помощью этого объекта можно будет использовать методы и свойства формы Form3 .

Данной форме отвечают файлы с именами « Unit3.h «, « Unit3.cpp » и « Unit3.dfm «.

Сначала осуществим настройку свойств формы Form3 так, как описано в п. 4:
– свойство Caption = «Ввод коэффициентов уравнений «;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать параметры шрифта: шрифт Tahoma , размер шрифта 12 .

Для построения формы ввода коэффициентов уравнений используем такие компоненты:
– два компонента типа TLabel . Автоматически будут созданы объекты с такими именами: label1 и label2 ;
– компонент типа TStringGrid (рис. 13) для ввода коэффициентов, которые размещаются в левой части системы уравнений.

Компонент TStringGrid размещается во вкладке Additional панели инструментов « Tool Palette «. Создается объект с именем StringGrid1 ;
– компонент типа TStringGrid (рис. 13) для введения коэффициентов, которые размещаются в правой части системы уравнений. Создается объект с именем StringGrid2 ;
– два компонента типа TButton (кнопки « » и « Продолжить >> «). Создаются два объекта с именами Button1 и Button2 .

Рис. 13. Компонент TStringGrid на палитре компонент

После размещения компонент и корректировки их размеров, форма Form3 будет иметь приблизительно следующий вид (рис. 14).

Рис. 14. Форма Form3

Формируем свойства компонент формы Form3:
– в компоненте Label1 свойство Caption = « Коэффициенты в левой части уравнения «;
– в компоненте Label2 свойство Caption = «Правая часть» ;
– в компоненте Button1 свойство Caption = « ;
– в компоненте Button2 свойство Caption = «Далее >>» .

Формируем свойства компонентов типа TStringGrid :
– в компоненте StringGrid1 свойство FixedCols = 0 (число фиксированных колонок);
– в компоненте StringGrid1 свойство FixedRows = 0 (число фиксированных строк);
– в компоненте StringGrid2 свойство FixedCols = 0 ;
– в компоненте StringGrid2 свойство FixedRows = 0 ;
– в компоненте StringGrid1 выбираем вкладку Options и устанавливаем опцию goEditing в значение « true «;
– в компоненте StringGrid2 во вкладке Options опция goEditing = « true «.

Рис. 15. Установление опции goEditing во вкладке Options компонента StringGrid1

После выполненных действий, форма Form3 будет иметь вид как показано на рисунке 16.

Рис. 16. Форма Form3 после окончательного формирования

5.2. Программирование обработчиков событий формы Form3 .

Программируем обработчики событий OnClick клика на кнопках Button1 и Button2 формы Form3 .

Листинг обработчиков событий приведен ниже.

6. Создание формы вывода результата.

Последней в приложении создается форма, которая будет выводить результат вычислений. Процесс создания и сохранения формы подробно описан здесь. При сохранении формы оставляем имя по умолчанию « Unit4.cpp «.

В результате получаем объект с именем Form4 .

Новосозданная форма Form4 описывается в файле « Unit4.dfm «. Также форме отвечают файлы « Unit4.h » и « Unit4.cpp «.

6.1. Построение формы Form4 .

Сначала настраиваем свойства формы Form4 :
– свойство Caption = «Результат» ;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать следующие параметры шрифта: шрифт Tahoma , размер шрифта 12 .

Также корректируем размеры формы.

Следующим шагом идет размещение на форме компонент.

Размещаем на форме следующие компоненты (рис. 17):
– один компонент типа TLabel ;
– два компонента типа TStringGrid ;
– один компонент типа TButton .

Корректируем размеры и позиции компонент для удобного отображения.

После размещения компонент будут созданы объекты с такими именами: Label1 , StringGrid1 , StringGrid2 , Button1 . В компоненте StringGrid1 выводятся номера переменных величин x в уравнении. В компоненте StringGrid2 выводятся значения решения системы уравнений.

Настраиваем компоненты формы следующим образом:
– в компоненте Label1 свойство Caption = «Решение системы» ;
– в компоненте Button1 свойство Caption = «OK» ;
– в компоненте StringGrid1 свойства FixedCols = 0 и FixedRows = 0 ;
– в компоненте StringGrid2 свойства FixedCols = 0 и FixedRows = 0 .

После размещения и настройки компонент, форма Form4 будет иметь вид, как показано на рисунке 17.