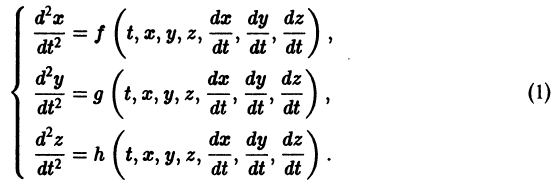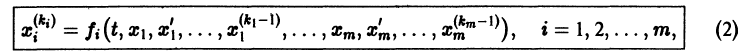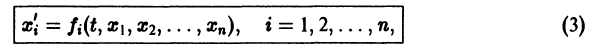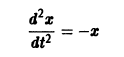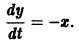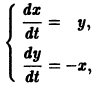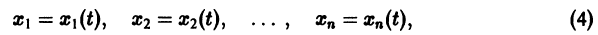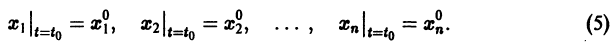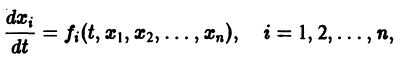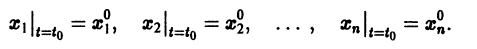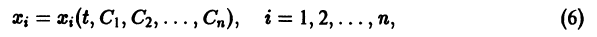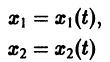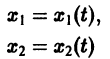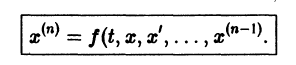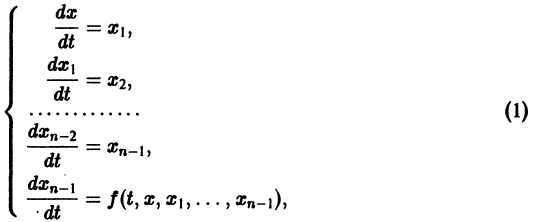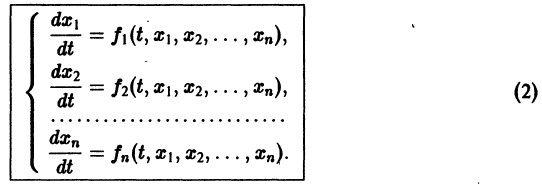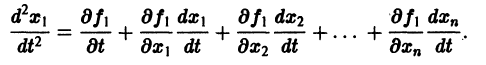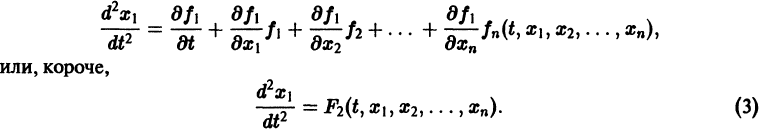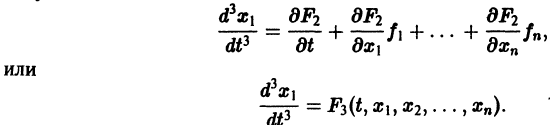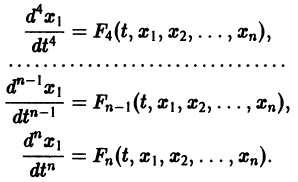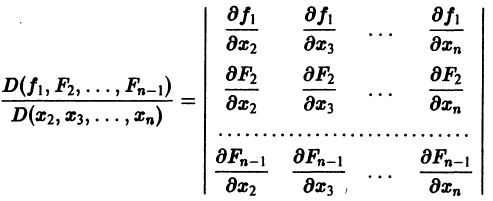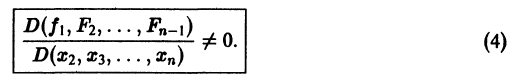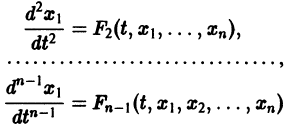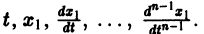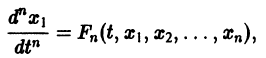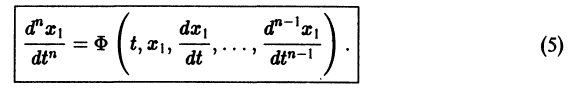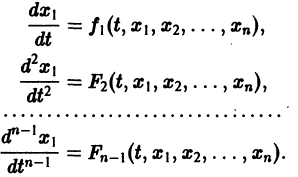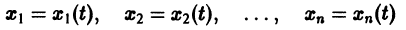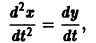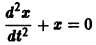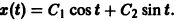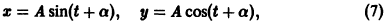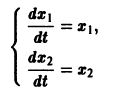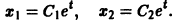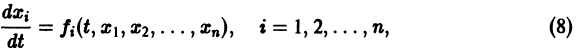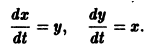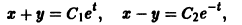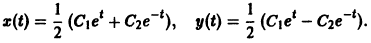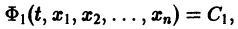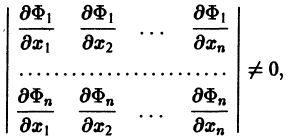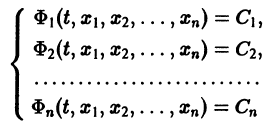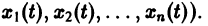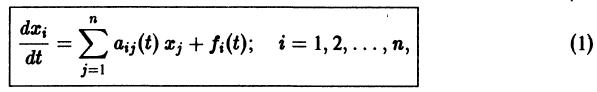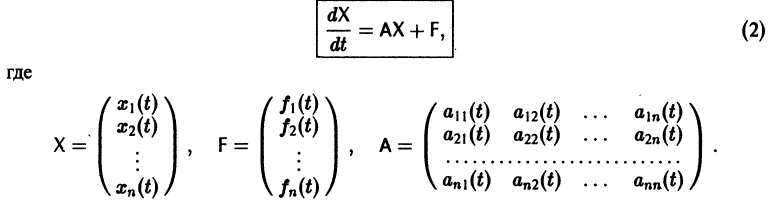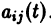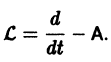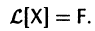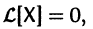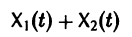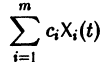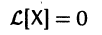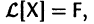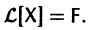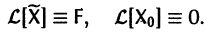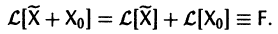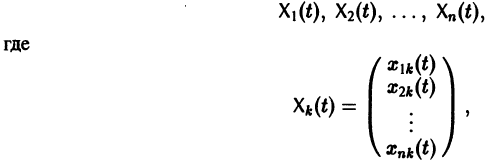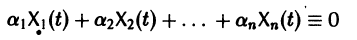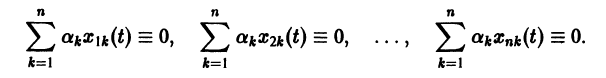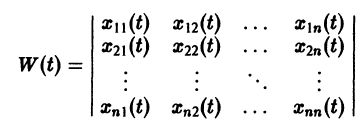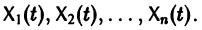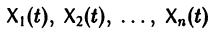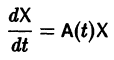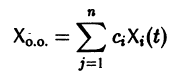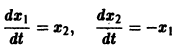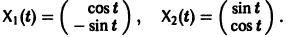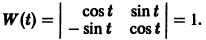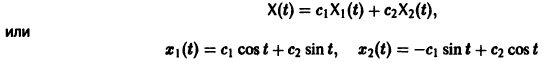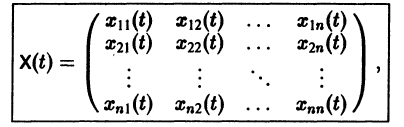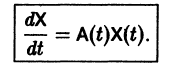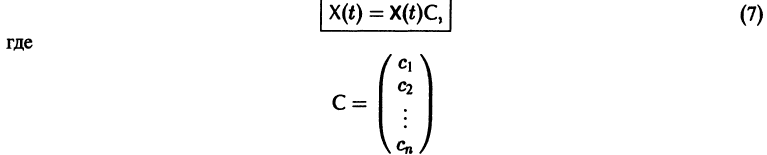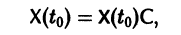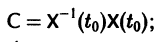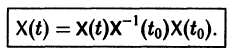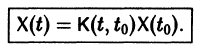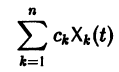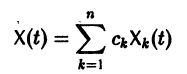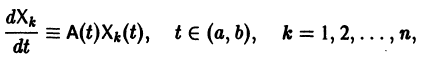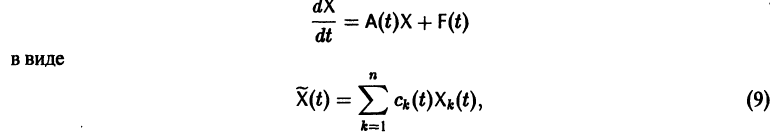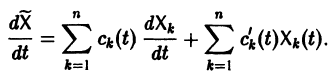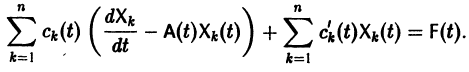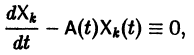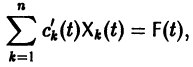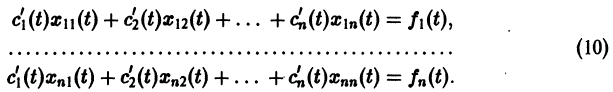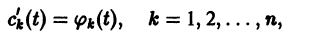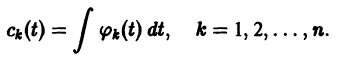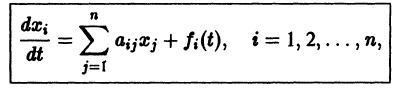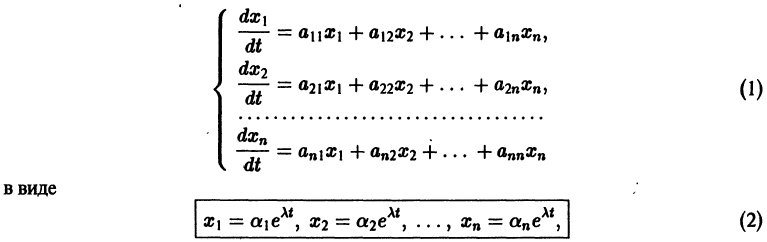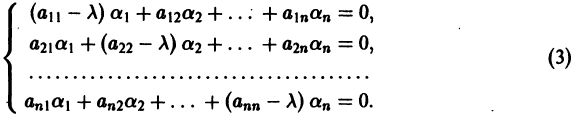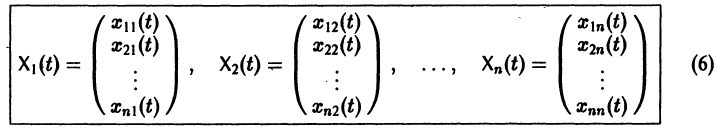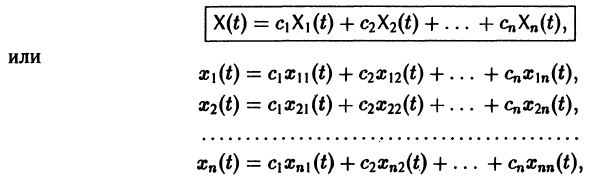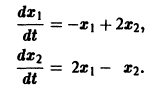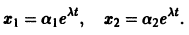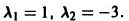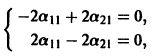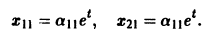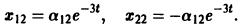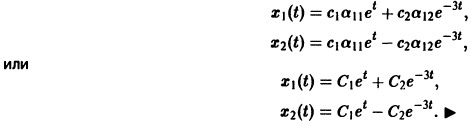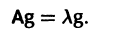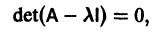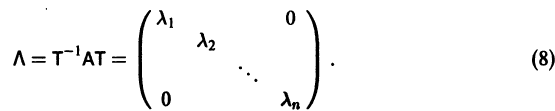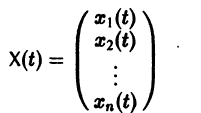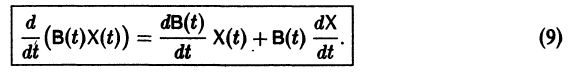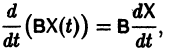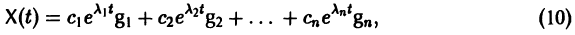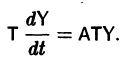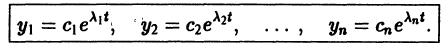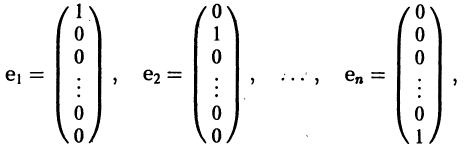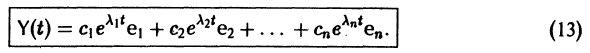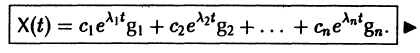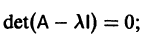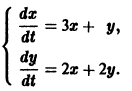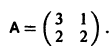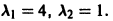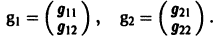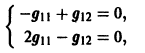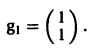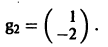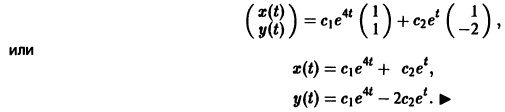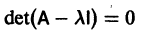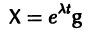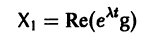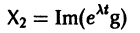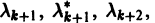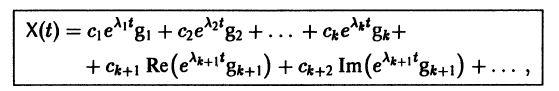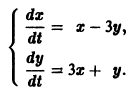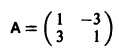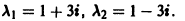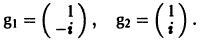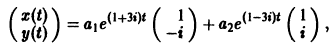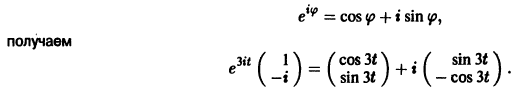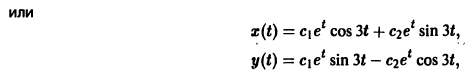Решение систем из трех дифференциальных уравнений

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 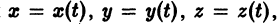выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 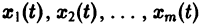аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

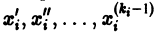
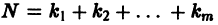
Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив 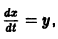в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

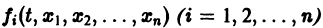
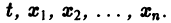
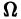
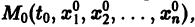
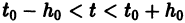
и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

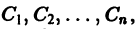
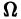
зависящих от t и n произвольных постоянных называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях 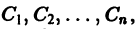система функций (6) обращает уравнения (3) в тождества,

2) в области 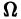функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных 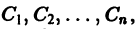называются частными решениями.

Обратимся для наглядности к нормальной системе двух уравнений,

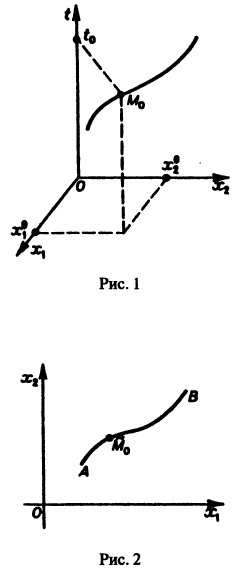
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 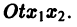Решение

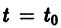
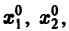
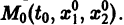
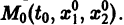
системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

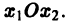
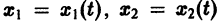
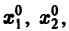
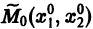
системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции 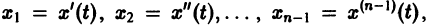заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

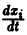
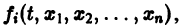
Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

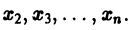
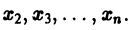
будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если 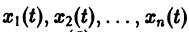есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 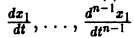и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно 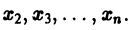т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

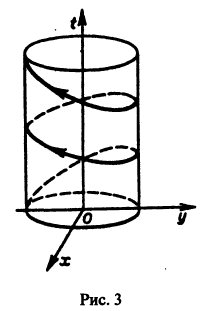
Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 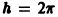и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

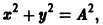
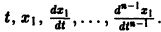
Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

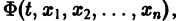
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

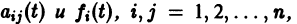
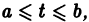
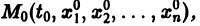
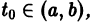
Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

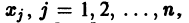
Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. 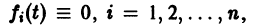на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

двух решений 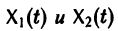однородной линейной системы уравнений является решением той же системы.

Следствие:

с произвольными постоянными коэффициентами сi решений 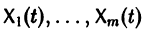линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если 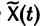есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора 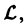получаем

Это означает, что сумма 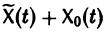есть решение неоднородной системы уравнений

Определение:

называются линейно зависимыми на интервале a

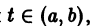
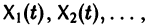
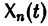
при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

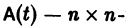
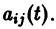
где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а

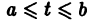
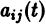
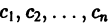
с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а

() — произвольные постоянные числа).

Пример:

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения 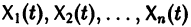системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

Матрица 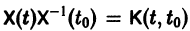называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 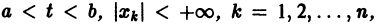линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке 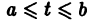коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения 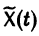неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

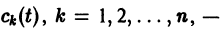
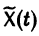
где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя 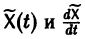в (2), получаем

то для определения 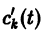получаем систему

или, в развернутом виде,

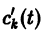
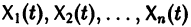
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где 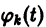— известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения 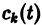в (9), находим частное решение системы (2)

(здесь под символом 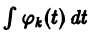понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты 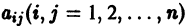— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

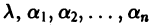
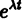
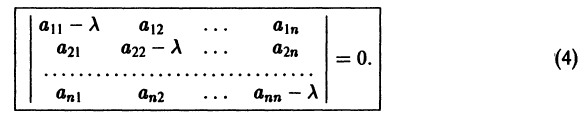
где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 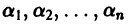имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

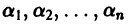
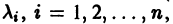
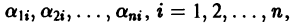
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 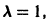получаем

откуда а21 = а11. Следовательно,

Полагая в 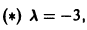находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

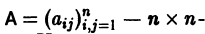
Напомним некоторые понятия из линейной алгебры. Вектор 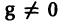называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

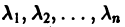
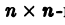
Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

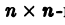
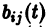
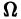
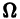
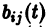
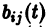
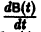
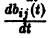
Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как 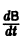есть нуль-матрица.

Теорема:

Если собственные значения 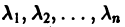матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

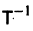
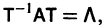
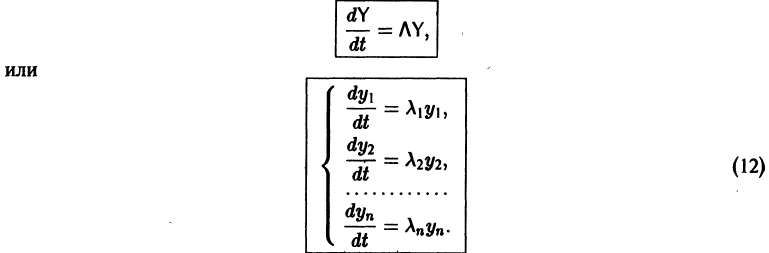
Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь 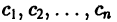— произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 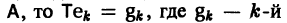собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения 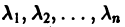матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 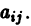системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

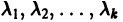
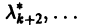
где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

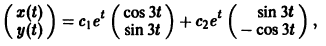
где с1, с2 — произвольные действительные числа.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Понятие о системах дифференциальных уравнений

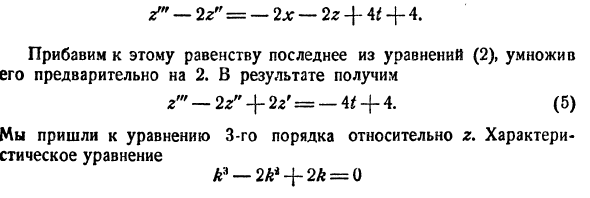
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Системы дифференциальных уравнений

Этот раздел мы решили посвятить решению систем дифференциальных уравнений простейшего вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 , в которых a 1 , b 1 , c 1 , a 2 , b 2 , c 2 — некоторые действительные числа. Наиболее эффективным для решения таких систем уравнений является метод интегрирования. Также рассмотрим решение примера по теме.

Решением системы дифференциальных уравнений будет являться пара функций x ( t ) и y ( t ) , которая способна обратить в тождество оба уравнения системы.

Рассмотрим метод интегрирования системы ДУ d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 . Выразим х из 2 -го уравнения системы для того, чтобы исключить неизвестную функцию x ( t ) из 1 -го уравнения:

d y d t = a 2 x + b 2 y + c 2 ⇒ x = 1 a 2 d y d t — b 2 y — c 2

Выполним дифференцирование 2 -го уравнения по t и разрешим его уравнение относительно d x d t :

d 2 y d t 2 = a 2 d x d t + b 2 d y d t ⇒ d x d t = 1 a 2 d 2 y d t 2 — b 2 d y d t

Теперь подставим результат предыдущих вычислений в 1 -е уравнение системы:

d x d t = a 1 x + b 1 y + c 1 ⇒ 1 a 2 d 2 y d t 2 — b 2 d y d t = a 1 a 2 d y d t — b 2 y — c 2 + b 1 y + c 1 ⇔ d 2 y d t 2 — ( a 1 + b 2 ) · d y d t + ( a 1 · b 2 — a 2 · b 1 ) · y = a 2 · c 1 — a 1 · c 2

Так мы исключили неизвестную функцию x ( t ) и получили линейное неоднородное ДУ 2 -го порядка с постоянными коэффициентами. Найдем решение этого уравнения y ( t ) и подставим его во 2 -е уравнение системы. Найдем x ( t ) . Будем считать, что на этом решение системы уравнений будет закончено.

Найдите решение системы дифференциальных уравнений d x d t = x — 1 d y d t = x + 2 y — 3

Начнем с первого уравнения системы. Разрешим его относительно x :

x = d y d t — 2 y + 3

Теперь выполним дифференцирование 2 -го уравнения системы, после чего разрешим его относительно d x d t : d 2 y d t 2 = d x d t + 2 d y d t ⇒ d x d t = d 2 y d t 2 — 2 d y d t

Полученный в ходе вычислений результат мы можем подставить в 1 -е уравнение системы ДУ:

d x d t = x — 1 d 2 y d t 2 — 2 d y d t = d y d t — 2 y + 3 — 1 d 2 y d t 2 — 3 d y d t + 2 y = 2

В результате преобразований мы получили линейное неоднородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами d 2 y d t 2 — 3 d y d t + 2 y = 2 . Если мы найдем его общее решение, то получим функцию y ( t ) .

Общее решение соответствующего ЛОДУ y 0 мы можем найти путем вычислений корней характеристического уравнения k 2 — 3 k + 2 = 0 :

D = 3 2 — 4 · 2 = 1 k 1 = 3 — 1 2 = 1 k 2 = 3 + 1 2 = 2

Корни, которые мы получили, являются действительными и различными. В связи с этим общее решение ЛОДУ будет иметь вид y 0 = C 1 · e t + C 2 · e 2 t .

Теперь найдем частное решение линейного неоднородного ДУ y

d 2 y d t 2 — 3 d y d t + 2 y = 2

Правая часть записи уравнения представляет собой многочлен нулевой степени. Это значит, что частное решение будем искать в виде y

= A , где А – это неопределенный коэффициент.

Определить неопределенный коэффициент мы можем из равенства d 2 y

= 2 :
d 2 ( A ) d t 2 — 3 d ( A ) d t + 2 A = 2 ⇒ 2 A = 2 ⇒ A = 1

Таким образом, y

= 1 и y ( t ) = y 0 + y

= C 1 · e t + C 2 · e 2 t + 1 . Одну неизвестную функцию мы нашли.

Теперь подставим найденную функцию во 2 -е уравнение системы ДУ и разрешим новое уравнение относительно x ( t ) :
d ( C 1 · e t + C 2 · e 2 t + 1 ) d t = x + 2 · ( C 1 · e t + C 2 · e 2 t + 1 ) — 3 C 1 · e t + 2 C 2 · e 2 t = x + 2 C 1 · e t + 2 C 2 · e 2 t — 1 x = — C 1 · e t + 1

Так мы вычислили вторую неизвестную функцию x ( t ) = — C 1 · e t + 1 .

Ответ: x ( t ) = — C 1 · e t + 1 y ( t ) = C 1 · e t + C 2 · e 2 t + 1

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Системы дифференциальных уравнений

Во многих задачах математики, физики и техники требуется определить несколько функций, связанных между собой несколькими дифференциальными уравнениями.

Для этого необходимо располагать, вообще говоря, таким же числом уравнений. Если каждое из этих уравнений является дифференциальным, то есть имеет вид соотношения, связывающего неизвестные функции и их производные, то говорят о системе дифференциальных уравнений.

1. Нормальная система дифференциальных уравнений первого порядка. Задача Коши.

Определение. Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и их производные, причём в каждое из уравнений входит хотя бы одна производная.

Система дифференциальных уравнений называется линейной, если неизвестные функции и их производные входят в каждое из уравнений только в первой степени.

Линейная система называется нормальной, если она разрешена относительно всех производных

(1)

В нормальной системе правые части уравнений не содержат производных искомых функций.

Решением системы дифференциальных уравнений называется совокупность функций удовлетворяющих каждому из уравнений этой системы.

Равенства при называются начальными условиями системы дифференциальных уравнений.

Часто начальные условия записывают в виде

Общим решением (интегралом) системы дифференциальных уравнений называется совокупность «n» функций от независимой переменной x и «n» произвольных постоянных C1 , C2 , …,Cn:

(2)

которые удовлетворяют всем уравнениям этой системы.

Чтобы получить частное решение системы, удовлетворяющее заданным начальным условиям , надо из уравнений (2) определить соответствующие начальным условиям значения постоянных C10 , C20 , …,Cn0 .

Задача Коши для системы дифференциальных уравнений состоит в том, чтобы найти такое решение, которое при принимало бы заданные значения .

Записывается задача Коши для нормальной системы дифференциальных уравнений следующим образом

Теорема существования и единственности решения задачи Коши.

Для нормальной системы дифференциальных уравнений (1) теорема Коши существования и единственности решения формулируется следующим образом:

Теорема. Пусть правые части уравнений системы (1), т. е. функции , (i=1,2,…,n) непрерывны по всем переменным в некоторой области D и имеет в ней непрерывные частные производные .

Тогда каковы бы ни были значения , принадлежащие области D, существует единственное решение системы (1) , удовлетворяющее начальным условиям

.

2. Решение нормальной системы методом исключения.

Для решения нормальной системы дифференциальных уравнений используется метод исключения неизвестных или метод Коши.

Пусть дана нормальная система

Дифференцируем по х первое уравнение системы

Заменяя производные их выражениями из системы уравнений (1), будем иметь

Дифференцируем полученное уравнение и поступая аналогично предыдущему, найдём

Продолжая далее таким же образом, получим уравнение

Итак, получили систему

(2)

Из первых п-1 уравнений определим y2 , y3 , … , yn , выразив их через

и

(3)

Подставляя эти выражения в последнее из уравнений (2), получим уравнения п-го порядка для определения y1 :

(4)

Решив это уравнение, найдём y1

(5)

Дифференцируя последнее выражение п-1 раз, найдём производные

как функции от . Подставляя эти функции в уравнения (4), определим y2 , y3 , … , yn .

Итак, получили общее решение системы (1)

(6)

Чтобы найти частное решение системы (1) удовлетворяющее начальным условиям при

надо найти из уравнения (6) соответствующие значения произвольных постоянных С1 , С2 , … , Сn .

Найти общее решение системы уравнений:

Продифференцируем первое уравнение:

Подставим в это выражение производную у¢ =2x + 2y из второго уравнения.

Подставим сюда у, выраженное из первого уравнения:

получаем решение системы:

3. Преобразование дифференциального уравнения порядка п к нормальной системе Коши.

Всякое уравнение п-го порядка

можно привести к системе уравнений первого порядка, если принять

за новые неизвестные функции.

С системами дифференциальных уравнений встречаются при изучении процессов, для описания которых одной функции недостаточно. Например, отыскание векторных линий поля требует реше­ния системы дифференциальных уравнений. Решение задач динамики криволинейного движения при­водит к системе трех дифференциальных уравнений, в которых неиз­вестными функциями являются проекции движущейся точки на оси координат, а независимой переменной — время. Позже вы узнаете, что решение задач электротехники для двух электрических цепей, нахо­дящихся в электромагнитной связи, потребует решения системы двух дифференциальных уравнений. Количество подобных примеров легко можно увеличить.

🔍 Видео

Системы дифференциальных уравнений. Часть 2Скачать

Системы дифференциальных уравненийСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Система с тремя переменнымиСкачать

Матричный метод решения систем уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Система дифференциальных уравнений. Операционный методСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать

ДУ Линейные системыСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Система неоднородных дифференциальных уравненийСкачать