Решение систем дифференциальных уравнений в excel (8 видео)

Обзор методов решения в Excel

Введение

Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

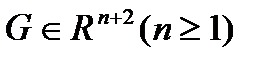
Решением этого уравнения на интервале I=[a,b] называется функция u(x).

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k_-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)

Обзор методов решения в Excel

1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка

Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

Содержание

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Сдвижков О.А.
Похожие темы научных работ по математике , автор научной работы — Сдвижков О.А.
EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM
Текст научной работы на тему «ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА»
Решение систем уравнений в среде Microsoft Excel
ХОД УРОКА
I. Организационная часть.
II. Повторение пройденного материала.
III. Объяснение нового.
IV. Практическая работа на компьютере.
V. Подведение итогов.
VI. Домашнее задание.
🌟 Видео

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА Текст научной статьи по специальности « Математика»

Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Аннотация научной статьи по математике, автор научной работы — Сдвижков О.А.

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1-го порядка и отдельных дифференциальных уравнений 1-го порядка.

Видео:Решение системы уравнений в ExcelСкачать

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

The current study presents program codes of custom VBA Excel functions that implement numerical methods for solving the Cauchy problem for a system of 1st order ordinary differential equations using the Euler and Runge-Kutta 4th order methods. The parameters of the functions are the initial and final values of the independent variable, an array of initial values of the dependent variables, and the number of steps. Program codes use dynamic arrays. Custom functions can be applied to the Cauchy problem and one of the 1st order differential equations. All of the custom functions have descriptions that explain their purpose. The article demonstrates the use of custom functions using specific examples of numerical solutions to the Cauchy problem of 1st order differential equations system and individual 1st-order differential equations.

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Текст научной работы на тему «ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА»

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА

Российский государственный университет туризма и сервиса, Пушкино МО, Россия * Корреспондирующий автор (oasdv[at]yandex.ru)

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1 -го порядка и отдельных дифференциальных уравнений 1 -го порядка.

Ключевые слова: система дифференциальных уравнений, задача Коши, численные методы, код, диалоговое окно.

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

Russian State University of Tourism and Service, Pushkino, Moscow Oblast, Russia * Corresponding author (oasdv[at]yandex.ru)

Keywords: system of differential equations, Cauchy problem, numerical methods, code, dialog box.

Системы обыкновенных дифференциальных уравнений 1-го порядка имеют большое прикладное значение [9]. Однако численные методы решения задачи Коши системы обыкновенных дифференциальных уравнений 1 -го порядка отличаются большой трудоемкостью [1], [2], [6]. Поэтому задача информатизации этих методов, доступной самому широкому кругу пользователей ПК, каким является круг пользователей Microsoft Office, несомненно, является актуальной.

Цель данного исследования — разработка на языке программирования VBA Excel [3], [4], [7] программных кодов пользовательских функций [10], которыми численно решается задача Коши системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта.

Программный код функции VBA Excel для решения методом Рунге-Кутта системы двух дифференциальных уравнений приведен в [5]. Пользовательские функции VBA Excel для численного решения задачи Коши обыкновенного дифференциального уравнения 1-го порядка приведены в [9].

1. Пользовательская функция ЭЙЛЕР

В методе Эйлера численного решения задачи Коши системы дифференциальных уравнений

dyL = f1(Х У1, У 2 Ут ) ах

= Л(Х У1, У 2 Ут ) „ 1Ч

йУт = /т (Х У1, У2 Ут )

У1( Хо) = У°, У2(Хо) = У20,-, Ут (Хо) = У0т (1.2)

на отрезке [хо, xo + n h] применяется формула:

у л = У ji-1 + h • f (хо + (i — 1)h Уи-1> У 2 i-iv, Ут1-1) (1.3)

j = 1, 2, . m; i= 1, 2, . n.

Правые части системы (1.1) в VBA Excel можно задать пользовательской функцией СИСТЕМ, листинг которой имеет вид:

Function СИСТЕМ (Массив As Variant)

‘массив состоит из значений^ — номера уравнения,х,у1,у2. yn Select Case Массив(1) Case 1

СИСТЕМ = /1(Массив(2), Массив(3), . Массив(т)) Case 2

СИСТЕМ = /2(Массив(2), Массив(3), . Массив(т))

СИСТЕМ = /п(Массив(2), Массив(3), . Массив(т)) End Select End Function

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция ЭЙЛЕР, код VBA Excel которой приведен в листинге 1, выполняет вычисления по формуле (1.3). Листинг 1. Код функции ЭЙЛЕР и ее описания Function ЭйЛЕР(Нач_х0, Конеч_х, Нач_у0(), Шагов) As Variant Dim n As Integer, m As Integer, x(), y(), z(), c() n = Шагов:т = иВоиМ(Нач_у0) ReDim z(1 To m, 0 To n):ReDim x(0 To n) ReDim y(1 To m + 2):ReDim c(1 To m) x(0) = Нач_x0:h = (Конеч_x — x(0)) / n For i = 1 To m z(i, 0) = Нач_у0® Next

Forj = 1 To n For i = 1 To m

y(1) = i: y(2) = x(0) + h * (j — 1) For r = 3 To m + 2 y(r) = z(r — 2, j — 1) Next

z(i, j) = z(i, j — 1) + h * СИСТЕМ(Массив)

For i = 1 To m c(i) = z(i, n) Next

ЭЙЛЕР = c End Function Sub InstallFunc2()

Application.MacroOptions Macш:=»ЭИЛЕР», Descriptions _ «Возвращает значения yi, полученные методом Эйлера» End Sub

В листинг 1 входят массивы:

z(1 To m, 0 To n)- двумерный массив значений функцийу1, у2, . ym в точках x0, x0+h, . x0+n h; x(0 To n) — массив значений х0, x0+h, . x0+nh;

y(1 To m + 2) — массив значений (i, x, y1, y2, . ym), где i — номер уравнения системы;

c(1 To m) — массив итоговых значений массива z.

Пример 1.1. Найти приближенные значения решения системы

с начальными условиями у (0) = 0, у2(0) = 1. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant)

Select Case Массив (1) Case 1

СИСТЕМ = Массив (4) Case 2

СИСТЕМ = Массив (3) End Select End Function

2. В диапазон А1:А5 вводятся значения, принимаемые переменной х: 0; 0,1; 0,2; 0,3; 0,4.

3. В диапазон В1:С1 вводятся начальные значения, принимаемые у1 и у2: 0 и 1.

4. Выделяется диапазон В2:С2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.1 — Применение функции ЭЙЛЕР в примере 1.1

5. Команда Ог^Ый +Enter возвращает в диапазоне В2:С2 результаты.

6. Копирование данных диапазона В2:С2 в диапазон В3:С5 завершает решение задачи (рис. 1.2).

Рис. 1.2 — Вид решения примера 1.1 функцией ЭЙЛЕР Пример 1.2. Найти приближенные значения решения системы

с начальными условиями у (0) = 1, у2(0) = 2, у3 (0) = 3. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4; 0,5.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant) Select Case Массив(1) Case 1

СИСТЕМ = Массив(4) + Массив(5) Case 2

СИСТЕМ = Массив(3) + Массив(5) Case 3

СИСТЕМ = Массив(3) + Массив(4)

End Select End Function

2. В диапазон А1:А6 вводятся значения, принимаемые х: 0; 0,1; 0,2; 0,3; 0,4; 0,5.

3. В диапазон B1:D1 вводятся начальные значения, принимаемые yi, у2, у3: 1, 2, 3.

4. Выделяется диапазон B2:D2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.3 — Применение функции ЭЙЛЕР в примере 1.2

5. Команда Ог1+8Ый +Бйег возвращает в диапазоне В2:Б2 результаты.

6. Копирование данных диапазона В2:Б2 в диапазон В3:Б6 завершает решение задачи (рис. 1.4).

J 0,2 2,07 2,88 3,69

4 0,3 2,727 3,456 4,185

5 0,4 3,4911 4,1472 4,8033

Б 0,5 4,38615 4,97664 15,56713

Рис. 1.4 — Вид решения примера 1.2 функцией ЭЙЛЕР

Функция Эйлер применима и к задаче Коши обыкновенного дифференциального уравнения 1 -го порядка. Пример 1.3. Найти приближенные значения решения задачи Коши

на отрезке [0, 1], разбивая отрезок на 10 равных частей. В этом случае код функции СИСТЕМ имеет вид: Function СИСТЕМ(Массив As Variant) СИСТЕМ = Массив(2) + Массив(3) End Function

Применение функции ЭЙЛЕР приводит к результатам, показанным на рисунке 1.3.

В с D Е F G Н 1 J К

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

1,1 1,22 1,362 1,5282 1,72102 1,943122 2,197434 2,487178 2,815895 3,187485]

Рис. 1.5 — Вид решения примера 1.3 функцией ЭЙЛЕР

2. Пользовательская функция РУНГЕ

В методе Рунге-Кутта четвертого порядка точности, которым численно решается задача Коши (1.1, 1.2):

k(2) = fj (x. + h / 2, уи + h ■ С / 2. уш + h • k« /2), (2.2)

k(? = fj (x + h /2, yH + h ■ k^ / 2. у„г + h ■ кП2) / 2), k(4 = fj(x + h,yw + h ■ *£>. уйг + h ■ О.

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция РУНГЕ, программный код VBA Excel которой приведен в листинге 2, выполняет вычисления по формулам (2.1), (2.2). Листинг 2. Код функции РУНГЕ и ее описания Function РУНГЕ(Нач_х, Конеч_х, Нач_у() As Variant, Шагов) _ As Variant

Dim n As Integer, m As Integer, h As Single, x(), y(), z(), c()

n = Шагов:т = иВоиМ(Нач_у)

ReDim z(1 To m, 0 To n):ReDim x(0 To n)

ReDim y(l To m + 2):ReDim c(1 To m)

Dim K(1 To 4) As Double

x(0) = Нач_x:h = (Конеч_х — x(0)) / n

For i = 1 To n Forj = 1 To m

y(1) = j: y(2) = x(0) + h * (i — 1) For r = 3 To m + 2 y(r) = z(r — 2, i — 1) Next

Массив = y:K(1) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(1) / 2 Next

K(2) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(2) / 2 Next

K(3) = h * СИСТЕМ(Массив):y(1) = j: y(2) = x(0) + h * i For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(3) Next

K(4) = h * СИСТЕМ(Массив)

z(j, i) = z(j, i — 1) + (K(1) + 2 * K(2) + 2 * K(3) + K(4)) / 6

For i = 1 To m c(i) = z(i, n) Next

РУНГЕ = c End Function Sub InstallFunc3()

Application.MacroOptions Macro:=»РУНГЕ», Description:= _ «Возвращает значения yi, полученн^1е методом Рунге-Кутта» End Sub

В листинге 2 массивы аналогичные массивам листинга 1, только:

K(1 To 4) — массив значений, вычисляемых по формулам (2.2).

Решение примера 1.1 с помощью функции РУНГЕ показано на рисунке 2.1.

3 0,2 0,210342 1,011061

4 0,3 0,316676 1,033103

5 0,4 0,425336 1,066488

Рис. 2.1 — Вид решения примера 1.1 функцией РУНГЕ Решение примера 1.2 с помощью функции РУНГЕ показано на рисунке 2.2.

Л I=РУН ГЕ(0; А2; [1; 2; 3 А2/0,1)>

2 0,1 1,5535 2,4423 3,3321

3 0,2 2,192731 2,933636 3,77449

4 0,3 2,940906 3,644213 4,34752

5 0,4 3,325591 4,451042 5,076493

6 0,5 4,330289 5,436502 5,992716

Рис. 2.2 — Вид решения примера 1.2 функцией РУНГЕ Решение примера 1.3 с помощью функции РУНГЕ показано на рисунке 2.3.

Рис. 2.3 — Вид решения примера 1.3 функцией РУНГЕ

Пример 2.1. Построить с помощью функции РУНГЕ графики численности популяций, описываемых системой Вольтерра — Лотка

при начальных условиях Х1(0)=3, х2(0)=1; параметр 1 принимает значения от 0 до 3.

Расчетная таблица строится по аналогии с таблицей примера 1.1, значения независимой переменной в диапазоне А1:А31, в ячейку В2 вводится формула =РУНГЕ(0;А2;;А2/0,01). По таблице строятся графики численности популяций (рис. 2.4).

4 3,5 3 2,5 2 1,5 1

0 0,5 1 1,5 2 2,5 3 Рис. 2.4 — Графики численности популяций

1. Программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка, публикуются впервые.

2. Как показывают примеры, применение рассматриваемых функций не вызывает трудностей, избавляет от больших объемов рутинных вычислений, позволяет получать результаты по такому сложному разделу, как численные методы решения систем дифференциальных уравнений, на современном (цифровом) уровне.

3. Рассматриваемые пользовательские функции будут полезны как в научных исследования, связанных с системами обыкновенных дифференциальных уравнений 1 -го порядка, так и в учебном процессе.

Конфликт интересов Conflict of Interest

Не указан. None declared.

Список литературы / References

1. Бахвалов Н.С. Численные методы. / Н. С. Бахвалов — М: Наука, 1975. — 632 с.

2. Березин И.С. Методы вычислений, т. II. / И. С. Березин, Н. П. Жидков — М.: ГИФМЛ, 1959. — 620 с.

3. Гарнаев А.Ю. MS Excel 2002: разработка приложений. / А. Ю. Гарнаев — СПб.: БХВ-Петербург, 2003. — 768 с.

4. Кузьменко В.Г. VBA 2003. / В. Г. Кузьменко — М: ООО «Бином-Пресс», 2004, 432 с.

5. Ларсен Р.У. Инженерные расчеты в Excel: Пер. с англ. / Р. У. Ларсен — М.: Издательский дом «Вильямс», 2002. -544 с.

6. Самарский А.А. Задачи и упражнения по численным методам: Учебное пособие. / А. А. Самарский, П. Н. Вабищевич, Е. А. Самарская — М.: Эдиториал УРСС, 2000. — 208 с.

7. Сдвижков О.А. Excel — VBA. Словарь-справочник пользователя / О. А. Сдвижков. — М.: Эксмо, 2008. — 224 с.

8. Сдвижков О.А. Пользовательские функции VBA Excel для численного решения задачи Коши ОДУ 1-го порядка / Сдвижков О.А. // Международный научно-исследовательский журнал, № 4 (106), 2021, Часть 1, стр. 35 — 40.

9. Эрроусмит Д. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями: Пер. с англ. / Д. Эрроусмит, К. Плейс. — М.: Мир, 1986. — 243 с.

10. Сдвижков О.А. DEcode (пользовательские функции) [Электронный ресурс]. — URL: https://oas.ucoz.com/load/odu_polzovatelskie_funkcii/1-1-0-35 (дата обращения: 20.01.2021)

Список литературы на английском языке / References in English

1. Bakhvalov N. S. Chislennye metody [Numerical Methods] / N. S. Bakhvalov-M: Nauka, 1975 — 632 p. [in Russian]

2. Berezin I. S. Metody vychislenijj, t. II. [Methods of Calculations, vol. 2] / I. S. Berezin, N. P. Zhidkov-M.: GIFML, 1959 — 620 p. [in Russian]

3. Garnaev A. Yu. MS Excel 2002: razrabotka prilozhenijj [MS Excel 2002: Application Development] / A. Yu. Garnaev -St. Petersburg: BKhV-Petersburg, 2003 — 768 p. [in Russian]

4. Kuzmenko V. G. VBA 2003 / V. G. Kuzmenko-M: «Binom-Press» LLC, 2004, 432 p. [in Russian]

5. Larsen R. U. Inzhenernye raschety v Excel: Per. s angl. [Engineering Calculations in Excel: Translation from English] / R. U. Larsen-M.: Publishing house «Vilyams», 2002 — 544 p. [in Russian]

6. Samarsky A. A. Zadachi i uprazhnenija po chislennym metodam: Uchebnoe posobie [Problems and Exercises in Numerical Methods: A Textbook] / A. Samara, P. N. Vabishchevich, E. A. Samarskaya -M.: Ehditorial URSS, 2000 — 208 p. [in Russian]

7. Sdvizhkov O. A. Excel — VBA. Slovar’-spravochnik pol’zovatelja [Excel — VBA. Dictionary-User reference] / O. A. Sdvizhkov. — M.: Eksmo, 2008 — 224 p. [in Russian]

8. Sdvizhkov O. A. Pol’zovatel’skie funkcii VBA Excel dlja chislennogo reshenija zadachi Koshi ODU 1-go porjadka [Custom Excel VBA Functions For Numerical Solution of a First-Order Cauchy Ode] / O. A. Sdvizhkov // Mezhdunarodnyjj nauchno-issledovatel’skijj zhurnal [International Research Journal], No. 4 (106), 2021, Part 1, pp. 35-40 [in Russian]

9. Arrowsmith D. Obyknovennye differencial’nye uravnenija. Kachestvennaja teorija s prilozhenijami [Ordinary Differential Equations: A Qualitative Approach with Applications]: Translation from English / D. Arrowsmith, C. M. Place. — Moscow: Mir, 1986 — 243 p. [in Russian]

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение систем уравнений в среде Microsoft Excel

обучающие:

повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
повторение алгоритма решения систем уравнений;
формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;

развивающие:

формирование умений анализировать, выделять главное, сравнивать, строить аналогии;

воспитывающие:

осуществление эстетического воспитания;
воспитание аккуратности, добросовестности.

Тип урока: урок закрепления изученного материала и объяснения нового.

ХОД УРОКА

I. Организационная часть.

Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!

Ответ: “Знание – сила!”

Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)

Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).

II. Повторение пройденного материала.

Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)

Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.

III. Объяснение нового.

А. Решим систему графическим способом. Преобразуем данную систему . Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

Запишем алгоритм решения систем уравнений графическим способом:

1. Преобразовать систему уравнений, если это необходимо.

2. Задать начальные значения для Х.

3. Найти значение первой функции при заданных Х.

4. Найти значение второй функции при тех же Х.

5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.

6. Решение системы — точка пересечения графиков функций.

7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

Б. Решить систему уравнений . Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.

Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:

При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.

Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

1. Преобразовать систему уравнений, если это необходимо

2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

4. Выбрать команду Сервис – Поиск решения.

5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения

6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)

7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК

8. Решить систему уравнений, щелкнув кнопкой Выполнить