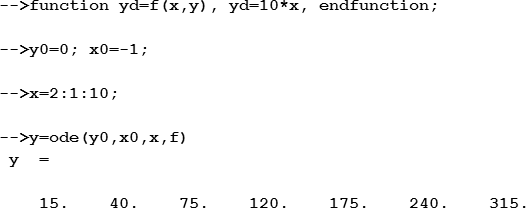Решение систем дифференциальных уравнений scilab (7 видео)

Решение дифференциальных уравнений в Scilab

Дифференциальные уравнения возникают в широком классе задач по описанию управляемых энергетических, промышленных и других процессов и комплексов. В настоящее время наблюдается бурное развитие робототехники, разработка и эксплуатация новых моделей роботов и промышленных манипуляторов, что стимулирует активные исследования по математической и прикладной теории управления, моделированию и конструированию управляемых систем.

Мы рассмотрим способы исследования сложных механических систем, моделируемых дифференциальными уравнениями. Рассмотрим способы конструирования управления нескольких видов для механической системы с двумя степенями свободы. А также, проведем визуализацию процесса стабилизации движения.

Содержание

Дифференциальные уравнения n-го порядка
6.2 Пример решения оду в Scilab
6.3 Cистемы дифференциальных уравнений
6.4 Примеры поиска решения систем ОДУ в Scilab
Scilab в свободном падении
Задача
Исходные данные
Модель-1 (без учета сопротивления воздуха)
Модель-2 (с учетом сопротивления воздуха)
Заключение
Основы работы с системой технических расчетов Scilab
🌟 Видео

Видео:scilab. Решение систем обыкновенных дифференциальных уравнений в бесплатном пакете.Скачать

Дифференциальные уравнения n-го порядка

Дифференциальным уравнением n-го порядка называется соотношение вида

Решением дифференциального уравнения является функция ( x(t) ), которая обращает это уравнение в тождество. Дифференциальные уравнения имеют бесконечное множество решений.

Чтобы однозначно определить решение некоторой задачи, необходимо задавать начальные условия. Количество таких условий должно совпадать с порядком уравнения. А решение, найденное для таких условий называется решением задачи Коши.

6.2 Пример решения оду в Scilab

Для решения обыкновенных дифференциальных уравнений (ОДУ) в Scilab используется
функция y = ode([type], y0, t0, t, func).
Разберём, что обозначает каждый из параметров у этой функции.

type — необязательный строковый параметр, с помощью которого можно выбрать метод решения ОДУ. Обычно этот параметр опускается.
t0 — скаляр начальный момент отрезка интегрирования. Обычно ( t0 = 0 ).
y0 — начальные условия. Отметим, что (y0 ) это вектор, размерность которого совпадает с порядком ОДУ. Так, для ОДУ 2-го порядка необходимо задать значения в начальный момент времени для функции и её производной, т.е. использовать запись (y0 = [0.1, 0.3]).
t — вектор, задающий узлы сетки, в которых ищем решение. Как правило, вектор t задается следующим образом t=t0:d:tmax, где (t0) — начальный момент отрезка интегрирования, (d) — шаг дискретизации, (tmax) — конечный момент отрезка интегрирования.
func — пользовательская функция, определяющая правую часть уравнения.
y — вектор решений.

Рассмотрим использование функции ode() на примере решения следующей задачи.

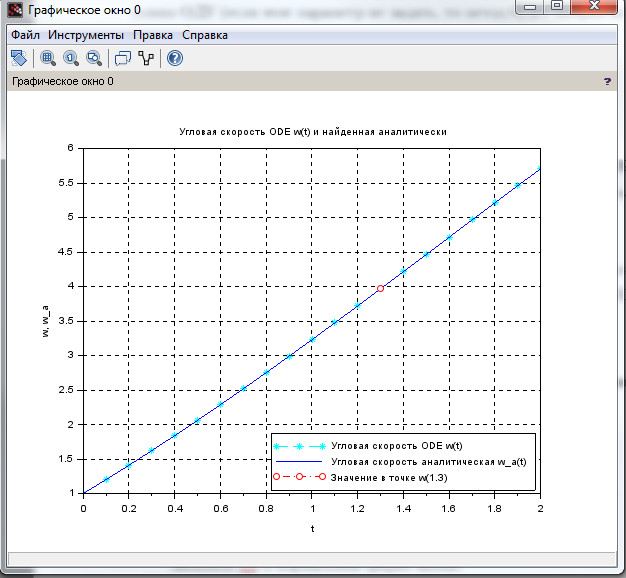
Найти угловую скорость ( omega(t) ) твердого тела вокруг неподвижной оси, если заданы начальная угловая скорость тела ( omega_0=1 ) и угловое ускорение ( varepsilon(t) = 2+0.5sin(t) ). Найти значение ( omega(t) ) в момент времени ( t_1=1.3 ). Построить график функций.

Рисунок 9. Сравнение графиков угловой скорости точки, по функции, найденной аналитическим и численным интегрированием. Красным кружком обозначено значение скорости точки в момент времени t=1.3c.

Угловая скорость точки может быть найдена из дифференциального уравнения

В нашем случае по условию задачи указаны следующие параметры для функции ode():
(t0=0 ) начальный момент времени,
(y0 = 1) начальное условие одно, т.к. порядок уравнения равен 1, это начальная угловая скорость тела ( omega_0=1 )
t=t0:h:tmax — вектор, задающий узлы сетки.

Результат работы программы представлен на рис.9, исходный код на листинге 15.

Отметим, что в данной программе фигурирует пользовательская функция aomega(t), представляющая собой угловую скорость, найденную аналитически с указанным начальным условием.

Функция ( f = 2t — 0,5cos(t) + 1,5 ) единственное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, то есть, функция (f) решение задачи Коши.

6.3 Cистемы дифференциальных уравнений

Для решения систем ОДУ в Scilab используется та же функция y = ode([type], y0, t0, t, func). Однако важным требованием является запись исследуемой системы в нормальной форме Коши.

Системой дифференциальных уравнений, записанной в нормальной форме Коши называется система, где слева стоят производные фазовых переменных, а справа некоторые функции, т.е. система вида

begin x_1′ = f_1(t,x_1. x_n) \ x_2′ = f_2(t,x_1. x_n) \ . \ x_n’ = f_n(t,x_1. x_n) end

Решением системы ОДУ является вектор x(t), который обращает это уравнение в тождество. Размерность вектора равна количеству уравнений в системе.

Стоит отметить, что дифференциальное уравнение n-ой степени может быть представлено в виде системы из n-уравнений первой степени, что позволяет решать задачу Коши для полученной системы ОДУ.

6.4 Примеры поиска решения систем ОДУ в Scilab

Решение системы ОДУ

Рассмотрим решение задачи Коши для системы уравнений

begin x’ = cos(xy) \ y’ = sin(x+ty) end

на интервале ( [0; 10]) и с начальными условиями (x(0)=0, y(0)=0 ).

Для поиска решения данной задачи, нам необходимо привести исходную систему к нормальному виду Коши. Для этого введём новые переменные ( (z1, z2) ) и сделаем необходимые переобозначения в исходной системе:

Рассмотрим решение задачи Коши для системы уравнений

begin z_1 = x \ z_2 = y end begin z_1′ = cos(z_1 z_2) \ z_2′ = sin(z_1 + t z_2) end

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 16. Обратите внимание, как происходит обращение к компонентам вектора решения ( z(t) ).

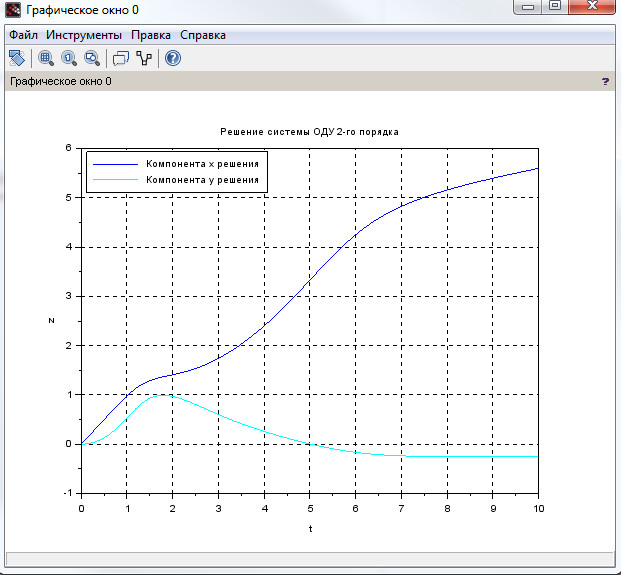
Для наглядной реализации сформировано графическое решение на рис. 10.

Рисунок 10. Графическое решение задачи Коши с помощью функции ode().

Решение системы ОДУ в матричной форме

Рассмотрим решение задачи Коши для системы уравнений, заданных в матричном виде

на интервале ( [0; 10] ) и начальными условиями ( y_1(0)=1, y_2(0)=0 ).

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 17. Обратите внимание, как происходит обращение к компонентам вектора решения (y(t)).

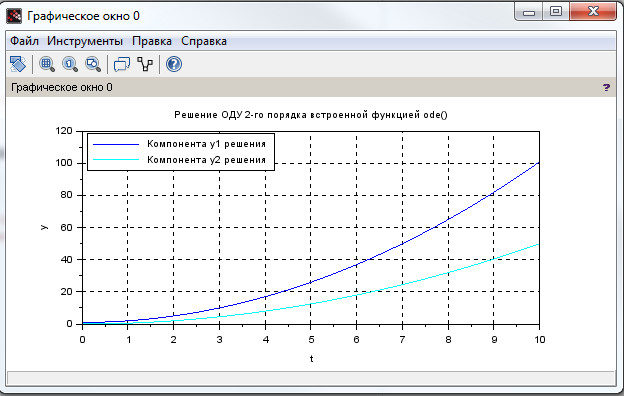
Для наглядной реализации сформировано графическое решение на рис. 11.

Рисунок 11. Графическое решение задачи Коши с помощью функции ode().

Решение ДУ 2-го порядка путём сведения к системе уравнений

Продолжим знакомиться с возможностями функции ode() на примере решения задачи механики на второй закон Ньютона.

Груз находится на пружине жёсткости ( c=12 ) H/м, масса груза ( m=68.7 ) кг. Определить закон движения груза, если на него действует сила ( F=100.5sin(2t) + ) H.

По 2-му закону Ньютона, движение груза описывается с помощью дифференциального уравнения 2-й степени, которое имеет вид:

и начальными условиями ( x(0)= 0, ; dot(0)= 0 ).

Как известно, ОДУ второго порядка сводится к системе в нормальной форме Коши, состоящей из двух уравнений первой степени. Введём новые переменные ( (z_1, z_2) ) и сделаем необходимые переобозначения в исходной системе:

begin z_1 = x \ z_2 = dot end begin dot_1 = z_2 \ dot_2 = (-cz_1 + F(t)) end

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 18. Обратите внимание, как происходит обращение к компонентам вектора решения ( y(t) ).

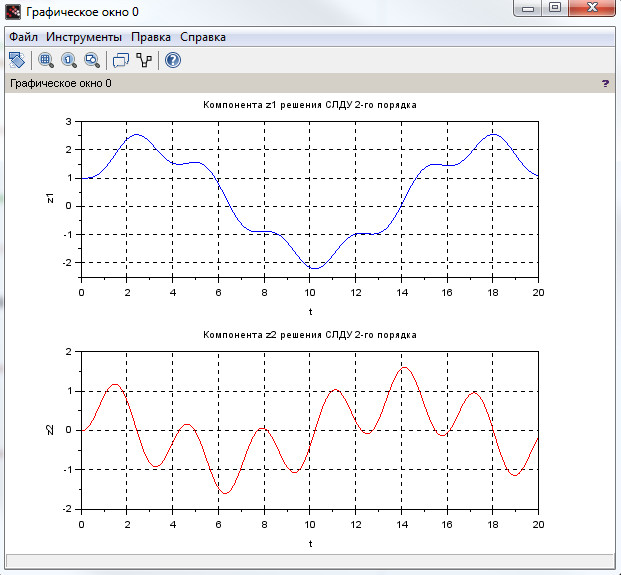
Для наглядной реализации сформировано графическое решение на рис. 12. Компонента ( z_1 ) представляет собой координату груза, а компонента ( z_2 ) — скорость груза.

Рисунок 12. Графики движения груза на пружине для компонент ( z_1 и z_2 ) соответственно.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Scilab в свободном падении

На днях с удивлением обнаружил, что на Хабре почти нет статей по Scilab. Между тем это достаточно мощная система компьютерной математики, открытая и кроссплатформенная, покрывающая широкий спектр инженерных и научных задач. В ряде ВУЗов (к примеру, УрФУ, ИТМО) ее используют для обучения студентов. Одной из самых насущных инженерных задач является решение дифференциальных уравнений (далее — ДУ). В данной статье я покажу как при помощи Scilab решать системы обыкновенных ДУ на примере моделирования знаменитого стратосферного прыжка Феликса Баумгартнера.

Как известно, свободное падение — это равнопеременное движение под действием силы тяжести, когда другие силы, действующие на тело отсутствуют или пренебрежимо малы. В быту часто свободным падением также называют движение в атмосфере Земли, когда на ускорение тела не влияют никакие силы, кроме силы сопротивления воздуха и силы тяжести. Именно таким расширенным пониманием мы и будем пользоваться в дальнейшем.

Видео:Scilab 2. ODEСкачать

Задача

Составить диф.уравнения (ДУ), описывающие существенные свойства полета Баумгартнера, решить их средствами Scilab и получить в явном виде зависимости дистанции и скорости от времени свободного падения.

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Исходные данные

Т.к. основная задача статьи — все-таки показать, как Scilab умеет решать ОДУ, а не получить идеально точную модель, увлекаться анализом экспериментальных данных (телеметрии), погрешностей и подгонкой мы особенно не будем. Однако для проверки адекватности модели несколько значений все же необходимо взять. Итак:

Высота прыжка — 39000м.
Дистанция свободного падения — 36402.6м.
Время свободного падения — 4 мин 20 сек.
За первые 20сек Баумгартнер набрал скорость 194 м/сек, через 50сек падения (на высоте 8447м) он развил рекордную скорость в 377м/сек, а к моменту раскрытия парашюта (т.е. через 260 сек полета) скорость падения снизилась до 77 м/сек.

Видео:Решение ДУ в ScilabСкачать

Модель-1 (без учета сопротивления воздуха)

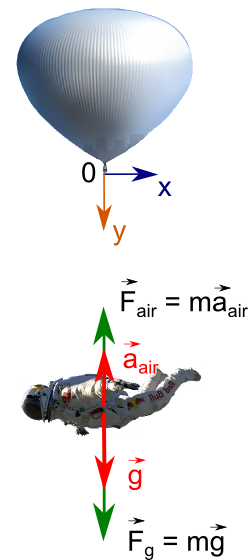
Начнем с простейшей модели, в которой есть только одна сила — сила притяжения Земли. Полагаем, что падение идет строго вертикально, начало координат размещено в точке начала прыжка, ось-y направлена вниз.

Ускорение экстремала, соответственно, равно ускорению свободного падения.

При этом по определению скорости:

Получили систему из двух обыкновенных ДУ. Решаем.

Воспользуемся функцией ode(), входящей в стандартный дистрибутив Scilab-а.
Согласно документации, ode решает явные обыкновенные дифференциальные уравнения, определенные как:

Прямо как в нашем случае. Слева должны быть производные 1го порядка.

Если же ДУ содержит производную 2го, 3го и пр. порядков, то нужно ввести замену(ы) и преобразовать одно уравнение с систему нескольких. Как мы на самом деле и сделали. Ведь ускорение — это 2я производная координаты по времени, от которой мы перешли к 1й производной, введя замену — переменную «скорость» равную dy/dt. Т.е.
от перешли к

Наконец-то переходим к коду (ссылка на github). Его можно писать в предлагаемом средой редакторе SciNotes, равно как и в любом другом текстовом редакторе. Можно также запустить оболочку без графики и вводить команды в консоли. На мой взгляд SciNotes удобнее подсветкой кода и интеграцией в среду разработки.

Первым делом нам нужно описать ДУ в виде функции на языке Scilab.

Затем задаем начальные условия.

После чего вызываем функцию-решатель ode(), передав ей на вход все созданное выше.

В матрице result в итоге окажуться значения искомых функций-решений данной системы ДУ, соответствующие точкам оси времени из указанного в t диапазона.

Посмотрим на то, что получилось в графической форме, а заодно выведем в консоль пару контрольных точек.

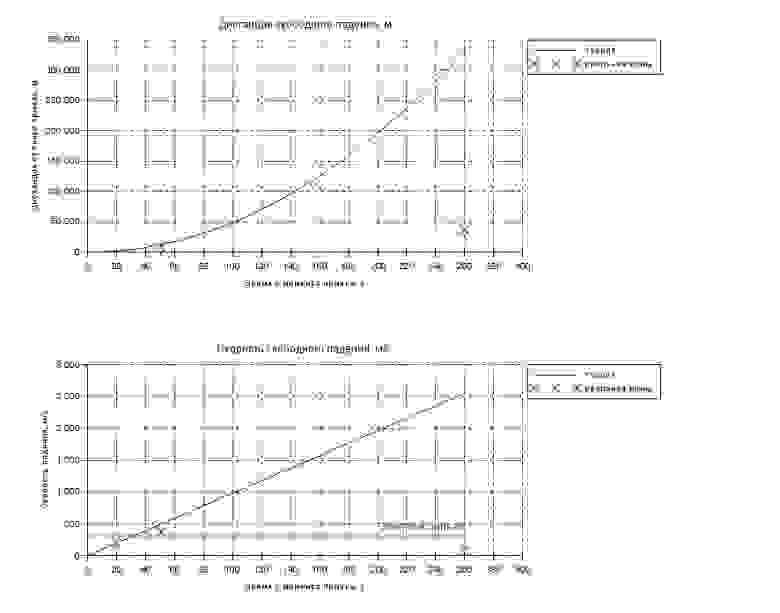
Получилась ожидаемая квадратичная зависимость координаты от времени.

Сверимся с практикой:
Cкорость через 50сек = 1762 км/ч (а должно быть 1357 км/ч).
Пройденный путь за 4мин.20сек = 331.3 км (а должно быть 36.4 км.).

Если со скоростью на начальном этапе прыжка, поморщившись, еще можно смириться, то итоговое пройденное расстояние превышено на порядок. Это объясняется тем, что неучтенное нами сопротивление воздуха на начальном участке полета действительно мало из-за разряженности стратосферы и наша простейшая модель худо-бедно справляется, но по мере снижения плотность атмосферы заметно увеличивается, ощутимо падает скорость падения и практика начинает категорически расходиться с теорией.

Если построить более подробный график, на который нанести также экспериментальные точки, то усугубляющееся со временем несоответствие данной модели и реальности станет еще более наглядным. В частности, скорость линейно возрастает, тогда как на практике она должна с определенного момента начать снижаться.

Исправим ситуацию, введя в модель силу сопротивления воздуха.

Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Модель-2 (с учетом сопротивления воздуха)

Атмосфера будет действовать на летящего с силой

где
с — коэффициент сопротивления
S — наибольшая площадь сечения, перпендикулярного направлению полета
density — плотность воздуха
v — скорость движения
Формула взята отсюда, где также можно почитать аналитическое решение

Нас интересует ускорение (хотя лучше было бы сказать замедление), которое F_air будет сообщать летящему вниз экстремалу, чтобы добавить поправку в первое уравнение системы.

По 2му закону Ньютона

С учетом данной поправки наша система примет вид

Решаем аналогичным образом. Описываем систему ДУ как Scilab-функцию.

Поскольку плотность атмосферы изменяется в зависимости от высоты, нам потребуется написать соответствующую функцию. Таблицу можно взять отсюда. А вообще есть ГОСТ 4401-81 Атмосфера стандартная. Параметры (с Изменением N 1).

Задаем начальные условия и решаем.

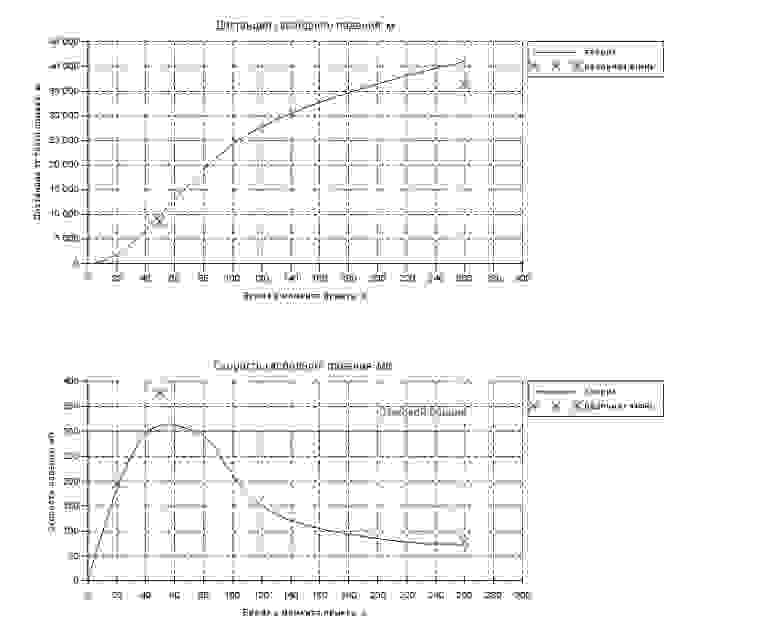
Построим график и посмотрим, что получилось.

Видим, что между 40-й и 70-й секундами пробьем звуковой барьер, в районе 50й секунды скорость достигнет максимума, после чего начнет снижаться. Набранной скорости не хватит, чтобы сгореть в атмосфере (на Хабре обсуждалось), кроме того к концу полета скорость снизится до величины, позволяющей безопасно открыть парашют. Что соответствует реальности.

Скорость — сравнение теории с экспериментом в контрольных точках

Время св.падения, с	Расчетная скорость, м/с	Фактическая скорость, м/с
20	183	194
50	312	377
260	73	77

Дистанция св.падения — сравнение теории с экспериментом в контрольных точках

Время св.падения, с	Расчетная дистанция, м	Фактическая дистанция, м
50	9853	8447
260	41049	36403

По скорости ошибка в среднем 27 м/с (7% от фактического рекорда), по дистанции свободного падения 3026 м (8% от фактически пройденной в св.падении дистанции). Для наших учебно-демонстрационных целей вполне приемлемо.

Видео:Практикум по реализации ДУ в ScilabСкачать

Заключение

Таким образом, мы на примере простой, но наглядной, мат. модели рассмотрели как при помощи Scilab решать ДУ, интерполировать, строить графики. Надеюсь эта статься будет полезна начинающим изучать Scilab, а кого-то быть может и подвигнет на дальнейшее применение Scilab в своей практической деятельности.

Видео:Решение уравнений в ScilabСкачать

Основы работы с системой технических расчетов Scilab

Интегралы

Для нахождения определенных интегралов в системе используется функция intg. В самом простом виде функция имеет такой синтаксис:

где f — подынтегральное выражение в виде текстовой строки или функция пользователя, xmin и xmax — это соответственно нижний и верхний пределы интегрирования.

Результат работы функции можно записать в переменную.

Напомним, что функция пользователя строится по определенным правилам: начинается с ключевого слова «function», после которого через запятую записывается имя функции, затем сама функция, а заканчивается описание функции пользователя ключевым словом «endfunction».

После этого достаточно вызывать функцию intg, которая возвращает значение определенного интеграла.

Кроме функции intg система имеет еще несколько функций для нахождения определенных интегралов:

intsplin — интегрирование при помощи сплайновой интерполяции;
inttrap — интегрирование при помощи метода трапеций;
integrate — интегрирование квадратурою.

Решение дифференциальных уравнений

Решение дифференциальных уравнений или систем дифференциальных уравнений в системе может осуществляться только в численном виде.

Для решения применяется функция ode, которая в самом простом виде имеет такой синтаксис:

y₀ — начальное условие: вещественное число для одного дифференциального уравнения или вектор для системы дифференциальных уравнений;

x₀ — начальное значение интервала интегрирования: действительное число для одного дифференциального уравнения или вектор для системы дифференциальных уравнений;

C — координаты оси x в виде: «начальная координата: шаг: конечная координата»;

f — функция пользователя — правая часть уравнения или системы уравнений.

Результатом работы функции является множество полученных численных значений решения.

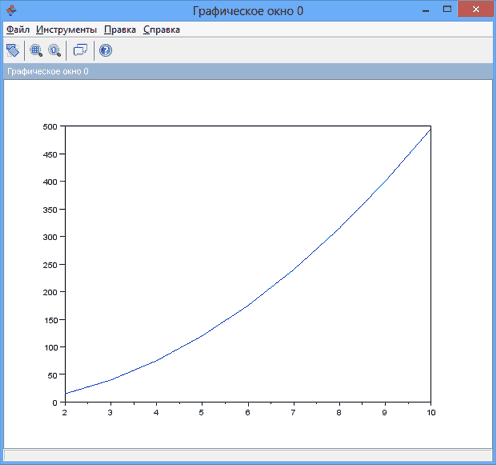
Пример. Найти общее решение обычного дифференциального уравнения первого порядка y’ — 10x = 0 на интервале [2,10] с начальным условием y₀ = -1.

Решение состоит в следующей последовательности команд:

В первой строке формируется функция пользователя, на которую в функции ode осуществляется ссылка. Поскольку она должна представлять собой правую часть дифференциального уравнения, то начальное уравнение преобразуется в вид y’ = 10x. Во второй строке задаются начальное условие y₀ = -1 и начальное значение интервала интегрирования, а в третьей — интервал изменения независимой переменной [2,10].

Получим графическое решение дифференциального уравнения.

Как нетрудно заметить, координатная сетка для оси x как раз и отображает интервал ее изменения [2,10].

Следует иметь в виду, что начальное значение x₀ должно быть меньше начального значения координаты оси x. В противном случае система генерирует ошибку наподобие приведенной ниже:

Как было отмечено выше, функция ode может быть использована для решения систем дифференциальных уравнений.

Пример. Решить систему дифференциальных уравнений 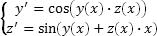на интервале с начальными условиями y₀ = 0 и z₀ = 0.

Решение будет состоять из такой последовательности команд:

Как видим, во время решения систем дифференциальных уравнений единственным отличием по сравнению с решением отдельных дифференциальных уравнений является создание двух векторов: правых частей уравнений (difur) и начальных условий (y0).

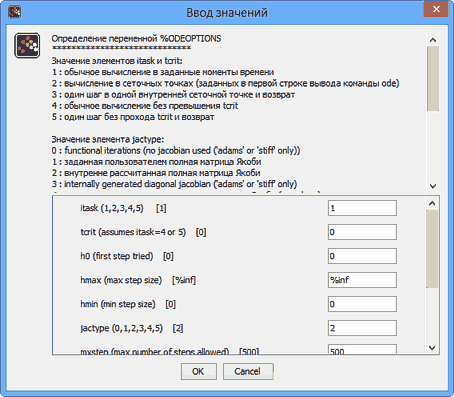
Scilab позволяет настроить «под себя» параметры вычисления для решения дифференциальных уравнений. Для этого он имеет специальное средство, обращение к которому осуществляется командою odeoptions(). Обратите внимание на то, что название команды вводится именно маленькими буквами. После обращения к функции появится диалоговое окно, в котором пользователь и задает соответствующие параметры вычисления для решения дифференциальных уравнений. Верхняя часть окна содержит информацию про назначения и значения по умолчанию, используемые системой для решения дифференциальных уравнений.

Выше было рассмотрено самое простое применение функции ode. Но она имеет достаточно большое количество аргументов, которые заметно увеличивают возможности пользователя для решения дифференциальных уравнений. Например, автоматически в процессе решения Scilab осуществляет выбор между методом прогнозирования и коррекции (nonstiff predictor — corrector) для нежесткой задачи и методом BDF (Backward Differentiation Formula) Адамса-Мултона для жестких задач. Вместе с тем, система позволяет и самостоятельно задать нужный метод. Для этого в функции используется специальный аргумент, записываемый первым в списке аргументов в символьном виде в двойных кавычках, например «adams».

Система предлагает несколько методов, в частности:

rk4 — адаптивный метод Рунге-угла 4-го порядка;
rkf — основывается на методе Рунге-Кута-Фельберга (Fehlberg’s Runge — Kutta) 4-5-го порядка точности с автоматической оценкой погрешности;
fix — метод Рунге-угла с фиксированным шагом.

XCOS — моделирование динамических систем

В составе системы имеется модуль Xcos, при помощи которого можно строить динамические модели. Доступ к нему осуществляется командою Инструменты > Визуальное моделирование XCOS, после чего появляется окно нового документа «Untitled» модуля Xcos и окно с палитрой инструментов моделирования.

Построение модели осуществляется в окне «Untitled» с использованием инструментов окна с палитрой инструментов моделирования.

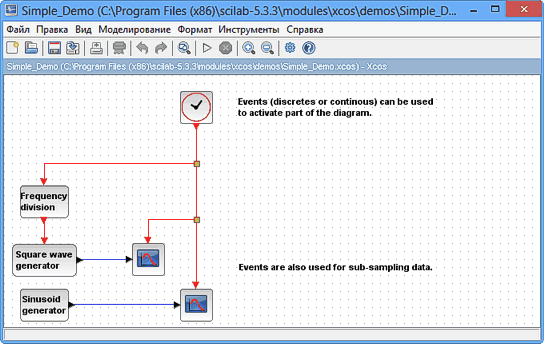
Scilab содержит библиотеку примеров построения моделей в разных отраслях, что дает возможность пользователям уяснить принципы построения моделей. Доступ к примерам осуществляется командою Справка > Примеры XCOS и последующим выбором в окне с примерами группы «XCOS». Примеры моделей сгруппированы по их функциональному назначению, например, «Electrical Systems» (электрические системы), «Control Systems» (системы управления) и т.п. Для выбора конкретной модели следует дважды щелкнуть на ее названии, что приведет к появлению окна с моделью.

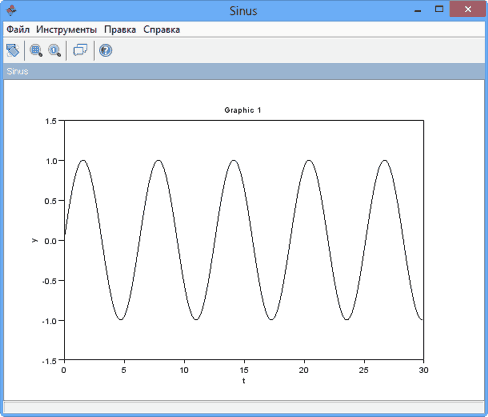
Для запуска модели на выполнение в этом окне следует выполнить команду Моделирование > Выполнить, что приведет к появлению графического окна, в котором и будет отображаться процесс моделирования.